Let v=-3i and w=2-4i. Find v+w
Answers
Answer:
2 - 7i
Step-by-step explanation:
v + w = -3i + 2 - 4i = 2 - 7i
Answer:
-7i+2Step-by-step explanation:
v + wGiven that v = -3i and w = 2-4i
Substituting them and simplifying,we obtain
-3i + 2-4iCollecting like terms,
-3i - 4i + 2-7i + 2Related Questions
You purchase a car in 2010 for $25,000. The value of the car decreases by 14% annually. Describe and correct the error in finidng the value of the car in 2015.
USE this to answer the question Please
what do you see?
What does it say?
What does it mean/
(conceptually & Contextually)
What mus be done?

Answers
Answer: its has to be .14
Step-by-step explanation:
Who has algebra 2 on edge ?
Answers
Answer:
i do, if uu need help hmu
Step-by-step explanation:
plz try your best do not quess

Answers
Answer:
43 2/5
Step-by-step explanation:
change each of the mixed fractions to improper fraction.
-11 2/3 = -31/3
-4 1/5 = -21/5.
Multiply them now:
-31/3 x -21/5 = 651/15
Then turn 651/15 to a mixed fraction because the question was in mixed fractions:
43 6/15 = 43 2/5 (simplified)
Please mark brainiest
Help pwease! Hope y’all are having a great day :)

Answers
Answer:
it don't make sence where is the table
Step-by-step explanation:
PELASE ANSWER QUICKLY!!!
Select the correct answer.
The finance manager at a college noticed that the average salary of the faculty members has been increasing for the past 10 years.
The average salary, in thousands of dollars, for arts and humanities faculty is modeled by function f, where x is the number of years since the manager began recording the data.

Answers
Answer:
As x approaches positive infinity, the average salary for science and engineering faculty will eventually be greater than the average salary for arts and humanities faculty.
Step-by-step explanation:
First consider the f(x) values on the graph as x increases on the interval 0 to 10 years. The average salary increases over the entire interval and reaches a maximum value of approximately $66,000.
Next create a table to show the values for function g.
0 16,188
1 18,366
2 21,101
3 25,000
4 40,000
5 55,000
6 58,899
7 61,634
8 63,811
9 65,650
10 67,257
The maximum value of function g is greater than the maximum value of function f. Therefore, as x approaches positive infinity, the average salary for science and engineering faculty will eventually be greater than the average salary for arts and humanities faculty.
A garage has 50 vehicles for sale, which are all
either new or second-hand.
32 of the vehicles are mopeds and the rest are
vans.
Of the mopeds, 8 are second-hand.
3 of the vans are new.
a) By copying and completing the frequency
tree below to show this information, work out
the value that should replace N in the frequency
tree.
b) In total, how many of the vehicles are
second-hand?
Answers
So, there are 34 second-hand vehicles in total.
What is probability?Probability is a measure of the likelihood or chance of an event occurring. It is expressed as a number between 0 and 1, where 0 indicates that the event is impossible, and 1 indicates that the event is certain to occur. For example, if the probability of rolling a 6 on a fair die is 1/6, it means that in the long run, out of every six rolls, one of them is expected to be a 6.
Here,
a) Here is the completed frequency tree:
|------- New (N)
|
Vans ----|------- Second-hand (18)
|
|------- Total (50)
|------- New (3)
|
Mopeds --|------- Second-hand (24)
|
|------- Total (32)
To fill in the missing value N, we can start by filling in the total number of vans:
|------- New (3)
|
Vans ----|------- Second-hand (N - 3)
|
|------- Total (50)
We know that there are 3 new vans and a total of 50 vehicles, so there must be 47 second-hand vehicles (50 - 3 = 47). Therefore, we can fill in N:
|------- New (3)
|
Vans ----|------- Second-hand (44)
|
|------- Total (50)
b) To find out how many vehicles are second-hand, we add up the number of second-hand vans and the number of second-hand mopeds:
18 (second-hand vans) + 16 (second-hand mopeds) = 34
To know more about probability,
https://brainly.com/question/30034780
#SPJ1
calcule
\(( + 4) \times ( + 2)\)
\(( - 5) \times ( - 3)\)
\(( + 6) \times ( + 2)\)
\(( - 4) \times ( - 3)\)
\(( + 2) \times ( + 5)\)
\(( - 6) \times ( - 3)\)
\(( + 7) \times ( + 3)\)
\(( - 8 \times ( - 4)\)
Answers
Answer:
1. 8
2. 15
3. 12
4. 12
5. 10
6. 18
7. 21
8. 32
Step-by-step explanation:
same sign add
How many 1/3 are in 1 2/3
Answers
there are 5 thirds.
There are three in a whole number one, and the two left over. Then you add em up!
Answer:
1 and 1/3
Step-by-step explanation:
1 2/3 = (1*3+2)/3 = 5/3. Therefore, 5/3 ÷ 1/3.
Add.
Your answer should be eth expanded polynomial in standard f
(5h – 8h)+(-2h – hè – 2h) =
Answers
Point B is between Points A and C on line segment AC. Use the information below to find
the length of AB and BC.
AB = 14x + 5
BC = 10x + 15
AC = 80
Please quickly !!!
Answers
What fraction is greater 6/8 or 3/2
Answers
Explanation: 3/2, or 1 1/2 is an improper fraction, while 6/8, or 3/4 is just a fraction.
So, 3/2 > 6/8
Answer:
3/2
Step-by-step explanation:
3/2 is greater than 1. 6/8 is less than one.
Solve for x.
(10−523)⋅(−2)+x=823
Answers
carlos es un arquitecto y esta construyendo una casa si ha construido 3/7 de la casa le falta para acabarla es lo mismo que llegar a 7/7
Answers
Answer:
Ok, sabemos que Carlos ha construido un 3/7 de una casa.
Queremos saber cuanto le falta para terminar de construirla.
Entonces podemos realizar el cálculo:
1 casa - lo que Carlos ya construyo = Lo que le falta.
Entonces:
1 casa - 3/7 de una casa = X
Podemos reescribir:
1 casa = 7/7 de una casas
así tenemos:
7/7 de una casa - 3/7 de una casa = X
(7/7 - 3/7) de una casa = X
4/7 de una casa = X
Así podemos concluir que a Carlos le falta construir 4/7 de una casa para acabar.
pls help this needs to be answered by today.

Answers
x+3x=144
4x=144
144/4=36
X=36
Hellppp will give brainliest to correct answer!thx in advance!

Answers
Answer:
A. x = 4
Step-by-step explanation:
Solve for x:
x + 4 (x + 5) = 40
4 (x + 5) = 4 x + 20:
4 x + 20 + x = 40
Grouping like terms, 4 x + x + 20 = (x + 4 x) + 20:
(x + 4 x) + 20 = 40
x + 4 x = 5 x:
5 x + 20 = 40
Subtract 20 from both sides:
5 x + (20 - 20) = 40 - 20
20 - 20 = 0:
5 x = 40 - 20
40 - 20 = 20:
5 x = 20
Divide both sides of 5 x = 20 by 5:
(5 x)/5 = 20/5
5/5 = 1:
x = 20/5
The gcd of 20 and 5 is 5, so 20/5 = (5×4)/(5×1) = 5/5×4 = 4:
Answer: x = 4
Triangle ABC is reflected over the line y = 1. What are the coordinates of B'? (–2, 3) (–2, 5) (2, –3) (4, –3)
Answers
Answer:
(-2,5)
Step-by-step explanation:
From the figure in the attachment it is clear that when point B will be reflected about the line y= -1. The point B becomes (-2,5)

Answer:b-(-2,5)
Step-by-step explanation:
Consider the following normal form game: L U 0,0 D 2-3 R 2, -2 1,-1 Assume that x > 0. Moreover, assume that Player Row chooses U with probability p and Player Column chooses L with probability q. a) Derive and plot players' best response functions (p on the horizontal axis and q on the vertical axis). b) Find all the Nash equilibria (pure and mixed strategies) of the above game. Illustrate your answer in a graph (p on the horizontal axis and q on the vertical axis. Comment. Consider now the following two-player simultaneous-move game, called the rock-paper-scissors-lizard game. R stands for rock, P for paper, S for scissors, and L for lizard. R beats S but loses against P and L; P beats R but loses against S and L; S beats P and L but loses against R; L beats R and P but loses against S. The payoff for winning is 1 and that for losing is -1; when both players choose the same strategy they each get 0. Assume that Player Row chooses R with probability r, P with probability p, and S with probability $ (similarly for Player Column). c) Write down the normal form representation of the game. d) Find all the Nash equilibria (pure and mixed strategies) of the game. Comment.
Answers
(a) Player Column's best response is given by:
BR_Column(p) = { L if p < 1/2, R if p > 1/2 (indifferent if p = 1/2)
(b) Where both players are indifferent between their available strategies.
(c) The normal form representation of the game is above.
(d) No player can gain an advantage by deviating from this strategy.
This equilibrium results in an expected payoff of 0 for each player.
(a) To derive the best response functions, we need to find the strategies that maximize the payoffs for each player given the mixed strategy of the other player.
Player Row's best response function:
If Player Column chooses L with probability q, Player Row's expected payoff for choosing U is 0q + 2(1-q) = 2 - 2q.
If Player Column chooses R with probability 1-q, Player Row's expected payoff for choosing U is 0*(1-q) + 1*q = q.
Therefore, Player Row's best response is given by:
BR_Row(q) = { U if q < 1/3, D if q > 1/3 (indifferent if q = 1/3)
Player Column's best response function:
If Player Row chooses U with probability p, Player Column's expected payoff for choosing L is 0p + 2(1-p) = 2 - 2p.
If Player Row chooses D with probability 1-p, Player Column's expected payoff for choosing L is 0*(1-p) + (-1)*p = -p.
Therefore, Player Column's best response is given by:
BR_Column(p) = { L if p < 1/2, R if p > 1/2 (indifferent if p = 1/2)
Plotting the best response functions on a graph with p on the horizontal axis and q on the vertical axis will result in two line segments: BR_Row(q) is horizontal at U for q < 1/3 and horizontal at D for q > 1/3, while BR_Column(p) is vertical at L for p < 1/2 and vertical at R for p > 1/2.
The two segments intersect at the point (p, q) = (1/2, 1/3).
(b) To find the Nash equilibria, we look for the points where the best response functions intersect. In this case, the only Nash equilibrium is at (p, q) = (1/2, 1/3), where both players are indifferent between their available strategies.
Now let's move on to the rock-paper-scissors-lizard game:
(c) The normal form representation of the game can be written as follows:
R P S L
------------------------
R | 0,0 -1,1 1,-1 1,-1
P | 1,-1 0,0 -1,1 1,-1
S | -1,1 1,-1 0,0 -1,1
L | -1,1 -1,1 1,-1 0,0
(d) To find the Nash equilibria, we look for any strategy profiles where no player can unilaterally deviate to improve their payoff.
In this game, there are no pure strategy Nash equilibria since each strategy can be countered by another strategy with a higher payoff.
However, there is a mixed strategy Nash equilibrium where each player chooses their actions with equal probabilities: r = p = s = l = 1/4.
In this case, no player can gain an advantage by deviating from this strategy.
This equilibrium results in an expected payoff of 0 for each player.
In summary, the rock-paper-scissors-lizard game has a unique mixed strategy Nash equilibrium where each player randomly chooses their actions with equal probabilities.
Learn more about Nash equilibrium from this link:
https://brainly.com/question/29398344
#SPJ11
Need help !!!!!!!!!!!
!!!!!!

Answers
Answer: B
Step-by-step explanation:
Angles θ and φ are angles in standard position such that:
sinθ = -5/13 and θ terminates in Quadrant III
tanφ = -8/15 and φ terminates in Quadrant II
Find sin(θ + φ).
Answers
When \(\theta\) terminates in quadrant III, both \(\cos\theta\) and \(\sin\theta\) are negative, and
\(\sin^2\theta+\cos^2\theta=1\implies\cos\theta=-\sqrt{1-\sin^2\theta}=-\dfrac{12}{13}\)
When \(\varphi\) terminates in quadrant II, \(\cos\varphi\) is negative and \(\sin\varphi\) is positive, so
\(1+\tan^2\varphi=\sec^2\varphi\implies\sec\varphi=-\dfrac{17}{15}\)
which gives
\(\cos\varphi=\dfrac1{-\frac{17}{15}}=-\dfrac{15}{17}\)
\(\tan\varphi=\dfrac{\sin\varphi}{\cos\varphi}=-\dfrac8{15}\implies\sin\varphi=\dfrac8{17}\)
Now,
\(\sin(\theta+\varphi)=\sin\theta\cos\varphi+\cos\theta\sin\varphi=-\dfrac{21}{221}\)
Use the distributive property to remove the parentheses.
-2( -6x-3v + 5)
Answers
Answer:
12x+6v-10
Step-by-step explanation:
-2(-6x-3v+5)
distribute -2 to the -6x
12x
distribute -2 to -3v
6v
distrbute -2 to 5
-10
For the past 10 periods, MAD was 25 units while total demand was 1,000 units. What was mean absolute percent error (MAPE)?
Multiple choice question.
10%
25%
50%
75%
Answers
The mean absolute percent error (MAPE) is 25%.
The mean absolute percent error (MAPE) is a measure of forecasting accuracy that quantifies the average deviation between predicted and actual values as a percentage of the actual values. In this case, the mean absolute deviation (MAD) is given as 25 units for the past 10 periods, and the total demand is 1,000 units.
To calculate the MAPE, we need to divide the MAD by the total demand and multiply by 100 to express it as a percentage. In this scenario, the MAPE is calculated as follows:
MAPE = (MAD / Total Demand) * 100
= (25 / 1,000) * 100
= 2.5%
Therefore, the MAPE is 2.5%, which means that, on average, the forecasts have a 2.5% deviation from the actual demand.
Learn more about: Percent
brainly.com/question/31323953
#SPJ11
Lauren and her brother had $50 to go to the state fair. They spent $10 on gas for the trip. If they're going to SPLIT the leftover money, how much money would each person get? O $40 each O $30 each O $10 each O $20 each
Answers
Answer:The would both get 20 dollars each
Step-by-step explanation:
Well you just half the 40 and what do you get?.... 20!
What is the volume of the cylinder? Use 3.14 for π, and round your answer to the nearest tenth. Enter your answer in the box

Answers
Answer:
235.5
Step-by-step explanation:
To get the radius you need to divide 5 by 2 and you would get 2.5. The formula for cylinder volume is πr^2h. 2.5^2 times 12 times π is 235.5
sat scores have a population mean of 1050 and standard deviation of 100. find the score that a student received if his/her score was the 98.71st percentile.
Answers
The score that a student received if his/her score was the 98.71st percentile is 1265 by using the Z-score formula.
The Z-score formula is:
Z = (X - μ) / σ
Where Z is the Z-score, X is the raw score, μ is the population mean, and σ is the standard deviation. In this case, the Z-score for the 98.71st percentile is 2.15 (from Z-score table), the population mean is 1050, and the standard deviation is 100. We can plug these values into the formula and solve for X:
2.15 = (X - 1050) / 100
2.15 * 100 = X - 1050
215 = X - 1050
X = 1265
Therefore, the score that a student received if his/her score was the 98.71st percentile is 1265.
Know more about Z-score here:
https://brainly.com/question/25638875
#SPJ11
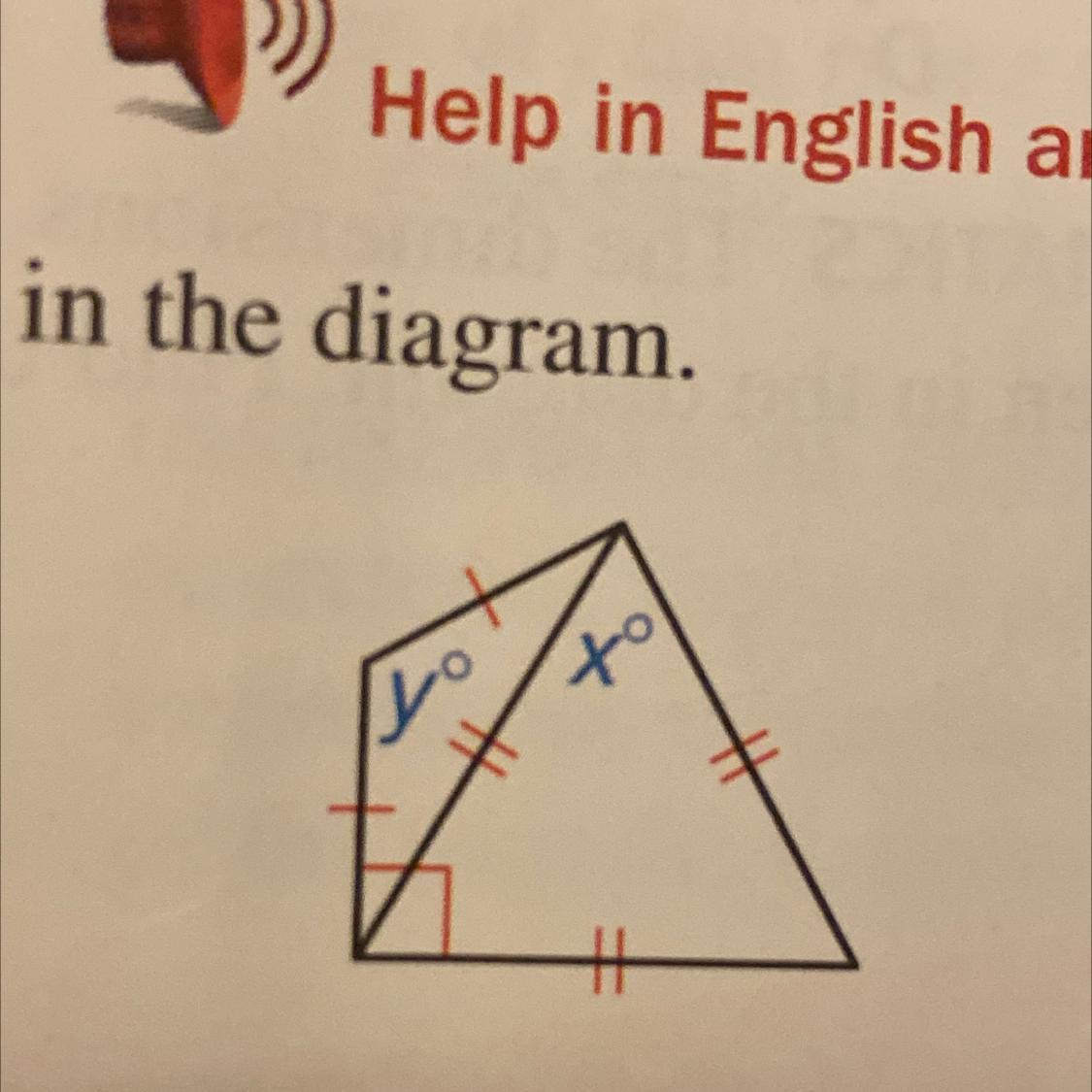
Find the values of x and y in the diagram
Answers
The values of x and y for the diagram are angle measures of triangles 60° and 120° respectively.
Interior angles of a triangleFor any triangle to be formed, its three interior angles must sum up to 180°. Thus the sum of the interior angles of a triangle is 180°
Considering, the equilateral triangle with one angle x, we can solve for the angle measure x as follows:
x + x + x= 180° {sum of interior angles of a triangle}
3x = 180°
x = 180°/3
x = 60°
For the isosceles triangle with angle y, one of its base angle is calculated as:
90° - x
90° - 60° = 30°
so;
y + 2(30) = 180° {sum of interior angles of a triangle}
y + 60° = 180°
y = 180° - 60°
y = 120°
Therefore, the values of x and y for the diagram are angle measures of triangles 60° and 120° respectively.
Know more about triangle here:https://brainly.com/question/7620723
#SPJ1
Courtney bought 3 packages of peanuts. Each package weighed 2 3/4 pounds. When she got home, Courtney divided the peanuts into 1/4 pound bags. How many bags did Courtney make?
Answers
Courtney bought a total of 3 x 2 3/4 = 8 1/4 pounds of peanuts. To find out how many 1/4 pound bags she can make, we need to divide 8 1/4 by 1/4. 8 1/4 ÷ 1/4 = 33.
Courtney bought 3 packages of peanuts, each weighing 2 3/4 pounds. To find the total weight of peanuts, multiply the weight per package by the number of packages: 2 3/4 × 3 = (11/4) × 3 = 33/4.
So, Courtney had 33/4 pounds of peanuts. She then divided them into 1/4 pound bags. To find out how many bags she made, divide the total weight of peanuts by the weight per bag: (33/4) ÷ (1/4) = 33/4 × 4/1 = 33 Courtney made 33 bags of peanuts.
Visit here to learn more about Pounds:
brainly.com/question/12983359
#SPJ11
NEEEEEEED HEEEEEEEELP !!!!!!!!!!!!!!!!! 13 POINTSSSSSS

Answers
the answer will be thirty three cm.
Need Help here Please!

Answers
Answer:
Step-by-step explanation:

To solve the given equation \(\sf x - y = 4 \\\), we can perform the following calculations:
a) To find the value of \(\sf 3(x - y) \\\):
\(\sf 3(x - y) = 3 \cdot 4 = 12 \\\)
b) To find the value of \(\sf 6x - 6y \\\):
\(\sf 6x - 6y = 6(x - y) = 6 \cdot 4 = 24 \\\)
c) To find the value of \(\sf y - x \\\):
\(\sf y - x = - (x - y) = -4 \\\)
Therefore:
a) The value of \(\sf 3(x - y) \\\) is 12.
b) The value of \(\sf 6x - 6y \\\) is 24.
c) The value of \(\sf y - x \\\) is -4.
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
does applying gradient boosting linear regressor multiple times give the same result as linear regression
Answers
No, applying gradient boosting linear regressor multiple times does not necessarily give the same result as linear regression.
Gradient boosting is an iterative machine learning algorithm that involves combining multiple weak models, such as decision trees, to create a strong predictive model. In each iteration of the algorithm, a new model is trained to predict the errors of the previous models, and the final prediction is the sum of the predictions of all the models.
On the other hand, linear regression is a parametric method that involves fitting a linear equation to the data, where the coefficients of the equation are estimated using the least squares method. While gradient boosting linear regression and linear regression both aim to predict a target variable based on a set of input variables, they use different approaches and assumptions, and their results may not be the same.
In particular, gradient boosting can be more effective than linear regression when the relationship between the input variables and the target variable is nonlinear or when there are complex interactions between the input variables. However, linear regression can be more interpretable and easier to implement than gradient boosting in some cases.
To know more about linear regression,
https://brainly.com/question/29665935
#SPJ11
If the train was traveling nonstop, how many miles would Smith
and Annie have traveled in 5.5 hours?
Answers
Therefore , the solution of the given problem of unitary method comes out to be pace of 50 mph, Smith and Annie would have covered 275 miles in 5.5 hours.
What is an unitary method?The data from this nanosection should be compounded by two in order to complete the task using the unitary method. In essence, the marked by either a set or the pigment parts of the unit method are skipped when a desired object is present. For forty pens, a variable charge of Inr ($1.01) would be required. It's possible that one country will have total influence over the approach taken to accomplish this.
Here,
If the railroad were moving at 50 mph continuously, it would cover 50 miles in an hour.
Thus, the train's route in 5.5 hours would be as follows:
=> 275 miles = 50 mph * 5.5 hours.
Thus, if the train had been moving continuously at a pace of 50 mph, Smith and Annie would have covered 275 miles in 5.5 hours.
To know more about unitary method visit:
https://brainly.com/question/28276953
#SPJ1
The complete question is "If the train was traveling nonstop at speed of 50 mph, how many miles would Smith
and Annie have traveled in 5.5 hours ?"