Let f(x)=x-1,h(x)=-x+4. Find (f o h)(4). (f o h)(4)=
Answers
Answer:
-1
Step-by-step explanation:
(f⚬h)(4) = f(h(4)) = f(-4+4) = f(0)
f(0) = 0-1 = -1
(f⚬h)(4) = -1
Related Questions
3x-14 when x equals 5 please help
Answers
Answer:
1
Step-by-step explanation:
15-14=1
Hope this helped!!
Step-by-step explanation:
3x-14 when x equals 5
3 (5) -14
15-14
x=1
Please answer and explain both in laymens terms

Answers
After considering the given data we come to the conclusion that the area to the left of z is 0.982, which is Option D. And the standard deviation of the given data is 87.6, which is Option C.
In order to calculate the area to the left of z=2.09 we have to apply the z-table:
1. Search for the row that starts with "2.0" in the leftmost column of the z-table.
2. Then for the column that starts with "0.09" in the top row of the z-table.
3. Here the value at the intersection of this row and column is 0.9821.
4. Finally round this value to three decimal places to get 0.982.
Hence , the area to the left of z=2.09 is 0.982.
Now for the second part of the question
Applying the given data set {10, 26, 84, 48, 250, 56}, we can evaluate the standard deviation as follows:
1. Evaluate the mean:
mean = (10 + 26 + 84 + 48 + 250 + 56) / 6 = 74
2. Applying subtraction of the mean from each data point:
{10 - 74, 26 - 74, 84 - 74, 48 - 74, 250 - 74, 56 - 74}
= {-64, -48, 10, -26, 176, -18}
3. Applying square of the result of step 2:
{(-64)², (-48)², (10)², (-26)², (176)², (-18)²}
= {4096, 2304, 100, 676, 30976, 324}
4. Exercising summation of the result of step 3:
4096 + 2304 + 100 + 676 + 30976 + 324
= 38176
5. Applying division of the result of step 4 by the number of data points (n):
standard deviation = √(38176 / (6 -1))
= √7625.2)
≈ 87.6.
Therefore, the answer is 87.6
To learn more about standard deviation
https://brainly.com/question/24298037
#SPJ1
The solution to an inequality is represented by the number line.
A number line going from negative 5 to positive 5. An open circle appears at positive 3. The number line is shaded from positive 3 to positive 5.
How can this same solution be written using set-builder notation?
Answers
The set builder notation of the solution inequality represented on the number line is; {x: 3< x <=5}.
What is the set builder notation representation of the solution?It follows from the task content that at point positive 3, there's an open circle which signifies that the number 3 is less than the solution.
And since the number line is shaded from positive 3 to 5, it follows that the maximum value in the solution set is 5.
The representation is therefore; {x: 3< x <=5}.
Read more on inequalities;
https://brainly.com/question/24644930
#SPJ4
On the number line, the solution inequality is represented by the notation x: 3=5, which is the set builder notation of the inequality.
This is further explained below.
What does the answer look like when represented using set builder notation?Given the information provided in the job, it is logical to conclude that at point positive 3, there will be an open circle. This will indicate that the number 3 will be lower than the answer.
And since the shading on the number line goes from positive 3 to 5, it follows that the highest value that can be found in the set of solutions is 5.
As a result, the representation is written as:
"x: 3 x = 5."
Learn more about the topic of inequality.
brainly.com/question/24644930
Can I please get some help I’ve been stuck on this question for a while!

Answers
Using the radius of the Ferris wheel and the angle between the two positions, the time spent on the ride when they're 28 meters above the ground is 12 minutes
How many minutes of the ride are spent higher than 28 meters above the ground?The radius of the Ferris wheel is 30 / 2 = 15 meters.
The highest point on the Ferris wheel is 15 + 4 = 19 meters above the ground.
The time spent higher than 28 meters is the time spent between the 12 o'clock and 8 o'clock positions.
The angle between these two positions is 180 degrees.
The time spent at each position is 10 minutes / 360 degrees * 180 degrees = 6 minutes.
Therefore, the total time spent higher than 28 meters is 6 minutes * 2 = 12 minutes.
Learn more on a Ferris wheel here;
https://brainly.com/question/30524034
#SPJ1
Which is equivalent to

Answers
Answer:
2·2·2·2 = 16
Step-by-step explanation:
everytime a number is raised by another, that means you are going to multiply the base number times itself as many times as the exponents tells you. this is a little but tricky to explain, so let me give you some examples:
2² → in this case the base number is 2 and the exponent is 2 as well, so you will multiply 2 times itself, 2 times:
2² = 2 · 2 = 4
2³ → in this case the base number is 2 and the exponent is 3, so you will multiply 2 times itself, 3 times:
2³ = 2 · 2 · 2 = 8
In the question asked, 2 is being raised by 4, so you will multiply 2 times itself, 4 times:
2^4 = 2·2·2·2 = 16
the same format will be used regardless of the base number and the exponent
i hope this helps! :)
what is 999.09344471 rounded to the nearest square kilometer?
Answers
The nearest kilometers to 999.09344471 km is 1000 km.
Given value is 999.09344471 Km.
We have to calculate the round off value to the nearest kilometers. we know that after the decimal if the value of tenth place is 5 or bigger than 5 then we add 1 to the tens place digit, this is the fundamental rule of rounding off.
Now on following this rule from the very right hand side up to the tenth place digit we come to the conclusion that only the value after the decimal (934) is to be rounded off which is (900).
So 999.09344471 km is finally becomes 999.900 km after rounding of to nearest hundredth value.
Again rounding off 999.900 km to nearest km so it becomes 1000 km.
The nearest kilometers to 999.09344471 km is 1000 km.
For more details on round off follow the link:
brainly.com/question/1093198
1
There are 31 students in a class.
14 of the students are female.
Find the percentage of the class that are female.
Give your answer to the nearest percent.
Effect
aths
Answers
Answer:
45.16%
Step-by-step explanation:
31 students is 100%
so, 14x100/31=45.16
Log20x=3 need the answer for algebra 2
Answers
Answer:
x = 50
Step-by-step explanation:
The diagram shows a circle drawn inside a square.
The circle touches the edges of the square.
12 cm
Calculate the shaded area.
Take pie to be 3.142 and write down all the digits given by your calculator.

Answers
Answer:
144 - 36×3.142 = 30.888
30.888 ÷4 = 7.722
Which statement is an example of the symmetric property of congruence?
A. If AKLM = APQR, then APQR = AKLM.
B. If AKLM = APQR, then APQR - ASTU.
X Х
C. If AKLM = APQR, and APQR - ASTU, then AKLM - ASTU.
D. AKLM = AKLM

Answers
Answer:
D.AKLM = AKLM
Step-by-step explanation:
because D.AKLM = AKLM is an example of the symmetric property of congruence
The statement which represents the symmetric property of congruence is given by if ΔKLM ≅ ΔPQR , then ΔPQR ≅ ΔKLM
What are Congruent Triangles?Transformations change the size or position of shapes. Congruent shapes are identical, but may be reflected, rotated or translated. Scale factors can increase or decrease the size of a shape. Congruent Triangles simply mean the triangles that possess the same size and shape
The three sides are equal (SSS: side, side, side)
Two angles are the same and a corresponding side is the same (ASA: angle, side, angle)
Two sides are equal and the angle between the two sides is equal (SAS: side, angle, side)
A right angle, the hypotenuse and a corresponding side are equal (RHS, right angle, hypotenuse, side)
Given data ,
Let the first triangle be represented as ΔKLM
Let the second triangle be represented as ΔPQR
Now , the measure of sides and angles be congruent
So , ΔKLM ≅ ΔPQR
From the symmetric property of congruence ,
If the first figure is congruent to second figure , the second figure is congruent to first figure
ΔKLM ≅ ΔPQR , then ΔPQR ≅ ΔKLM
Hence , the ΔKLM ≅ ΔPQR and they are congruent triangles
To learn more about congruent triangles click :
https://brainly.com/question/26131452
#SPJ5
In Mr. Romeo's class, a student must work on i-Ready for at least 4 hours per month to receive a grade of 100. Last month Sophia received a math grade of 100. Which inequality represents the number of hours Sophia spent working on i-Ready last month, where h represents the number of hours? (PLEASE HELP MEE!! GIVING 10 POINTS!)
A. h≥4
B. h>100
C. h≤100
D. h<4
Answers
The inequality that represents the number of hours Sophia spent working on i-Ready last month is h ≥ 4.
Option A is the correct answer.
We have,
The problem states that a student must work on i-Ready for at least 4 hours per month to receive a grade of 100.
Since Sophia received a math grade of 100, it means that she has met the requirement of working on i-Ready for at least 4 hours in the last month.
And,
The symbol "≥" means "greater than or equal to," indicating that Sophia worked for at least 4 hours.
Therefore,
The inequality that represents the number of hours Sophia spent working on i-Ready last month is h ≥ 4.
Learn more about inequalities here:
https://brainly.com/question/20383699
#SPJ1
Containers A (6cm, 5cm, 4cm), B (5cm, 4cm, 3 cm) and C (3cm, 3cm, 2 cm) are three rectangular containers. At first, container A is filled with water to its brim while containers B and C are empty. Next, some water from container A is poured into containers B and C so that container B is completely full while container C is half full. Find the height of the water left in container A..
Answers
<><><><><><><><><><><><><><><>
Will give brainliest, please help fast

Answers
Answer:
Converting the equation \(x^2-20x+13=0\) into completing the square method we get: \(\mathbf{(x-10)^2=87}\)
Step-by-step explanation:
we are given quadratic equation: \(x^2-20x+13=0\)
And we need to convert it into completing the square method.
Completing the square method is of form: \(a^2-2ab+b^2=(a-b)^2\)
Looking at the given equation \(x^2-20x+13=0\)
We have a = x
then we have middle term 20x that can be written in form of 2ab So, we have a=x and b=? Multiplying 10 with 2 we get 20 so, we can say that b = 20
So, 20x in form of 2ab can be written as: 2(x)(10)
So, we need to add and subtract (10)^2 on both sides
\(x^2-20x+13=0\\x^2-2(x)(10)+(10)^2-(10)^2+13=0\\(x^2-2(x)(10)+(10)^2) \:can\: be\: written\: as\: (x-10)^2 \\(x-10)^2-100+13=0\\(x-10)^2-87=0\\(x-10)^2=87\)
So, converting the equation \(x^2-20x+13=0\) into completing the square method we get: \(\mathbf{(x-10)^2=87}\)
The profit P(x) obtained by manufacturing and selling x units of a certain product is given by P(x) = 60x - x2. Determine the number of units that must be produced and sold to maximize the profit. What is the maximum profit?
Answers
Answer:
The number of units that must be produced and sold to maximize the profit is 30 units
\(30\text{ units}\)The maximum profit is;
\(\text{ \$900}\)Explanation:
Given that the profit P(x) obtained by manufacturing and selling x units of a certain product is given by;
\(P(x)=60x-x^2\)The maximum point is at;
\(P^{\prime}(x)=0\)Differentiating P(x);
\(\begin{gathered} P^{\prime}(x)=60-2x=0 \\ 60-2x=0 \\ 2x=60 \\ x=\frac{60}{2} \\ x=30 \end{gathered}\)The number of units that must be produced and sold to maximize the profit is 30 units
Substituting x into p(x);
\(\begin{gathered} P(30)=60(30)-30^2 \\ P(30)=900 \end{gathered}\)The maximum profit is;
\(\text{ \$900}\)Which geometric series converges?
CO
Σ(-3) 2-1
Η =1
O
Σ5-1) 2-1
CO
Ο Σ4(-02 - 1
H=1
CO
Σ06(-2) 2-1
h=1
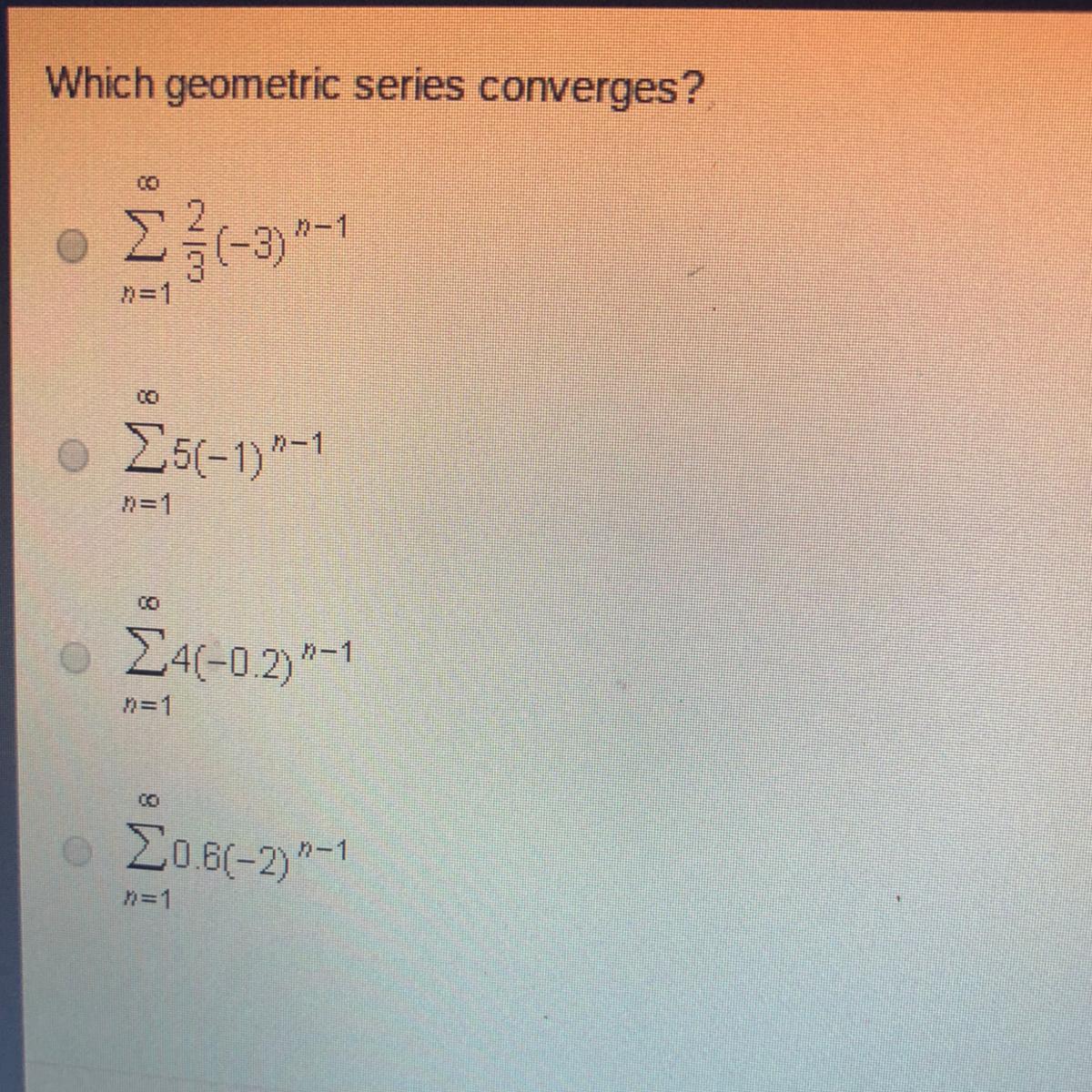
Answers
Answer:
its C
Step-by-step explanation:
i just did it on edge and plus its really not cool to post answers when you dont actually know the answer bc people that actually want to help cant bc there only two answers allowed per question. so please dont answer if your not trying to help.
The geometric series \(\sum_{n=1}^{\infty} 5(-1)^{n-1}\) converges to zero.
What is convergent and divergent geometric series?A mathematical term denoting an endless series of the form
a + ar + ar² + ar³ + ⋯, where r is referred to as the common ratio. The geometric series for a = 1 and r = 1/2, or 1 + 1/2 + 1/4 + 1/8 +, is a straightforward example.
A series is considered to be convergent if the partial sums gravitate to a certain value, also known as a limit.
In contrast, a divergent series is one whose partial sums do not reach a limit. The Divergent series usually approaches infinity.
From the given options let us try with \(\sum_{n=1}^{\infty} 5(-1)^{n-1}\).
\(= 5\sum_{n=1}^{\infty} (-1)^{n-1}.\)
\(= 5\sum_{n=1}^{\infty} (-1)^{n}.\frac{1}{-1}\).
\(= -5\sum_{n=1}^{\infty} (-1)^{n}.\)
= - 5[- 1 + 1 - 1 + 1 ...+ 1].
= - 5[0].
= 0.
learn more about geometric sequences here :
https://brainly.com/question/19235539
#SPJ7
The probability of getting heads on a single coin flip is ;
2
The probability of getting nothing but heads
on a series of coin flips decreases by
2
for each additional coin flip. Enter an exponential function for the
probability p(n) of getting all heads in a series of n coin flips. Give your answer in the form a (b)'. In the
event that a = 1, give your answer in the form (b)'.
Answers
Select the correct answer.
Which expression is equivalent to the given expression?
(3m^-4)^3(3m^5)
A.
B.
C.
D.

Answers
Answer:
\(d)\ \frac{81}{m^{7}}\)
Step-by-step explanation:
\((3m^-4)^3(3m^5)\)
First, simplify \((3m^{-4})^3\):
\((3m^{-4})^3\\\\3^3*m^{-4*3}\\\\27m^{-12}\)
\(27m^{-12}*3m^5\\\\27*3 *m^{-12+5}\\\\81m^{-7}\\\\81*\frac{1}{m^{7}} \\\\\frac{81}{m^{7}}\)
Hope this helps!
Jorge bought a crate of floor tiles for $95.94. The crate had 6 boxes of floor tiles. Each box contained 20 floor tiles.
Write and solve an equation to determine the cost per box, b. Then write and solve a second equation to determine the cost per tile, t, to the nearest cent. Show your work.
HELP!!
Answers
The solution is:
⇒ 6b = 95.94 (equation to determine cost of one box)
cost of one box 'b' = $`15.99
⇒ 12t = 95.94 (equation to determine cost of per tile)
cost of one tile t = $0.7995.
Given :
Jorge bought a crate of floor tiles for $95.94.
The crate had 6 boxes of floor tiles.
Each box contained 20 floor tiles .
To Find :
Write and solve equation to determine the cost per box'b'.
Write and solve a second equation to determine the cost per tile't'
Solution :
Cost of one box = b
There are 6 boxes
So, cost of 6 boxes = $ 6b
Since Jorge bought 1 crate( = 6 boxes) of cost $95.94
⇒ (equation to determine cost of one box)
⇒6b = 95.94
⇒b =15.99
Thus cost of one box = $`15.99
Since 1 box 20 floor tiles
So, 6 boxes (=1 crate) contain tiles = 6*20 = 120 tiles
We are given that cost of 1 crate( = 6 boxes = 120 tiles) is $95.94
Cost of one tile = t
Cost of 120 tiles = $120t
⇒ (equation to determine cost of per tile)
⇒12t = 95.94
⇒t = 0.7995.
Thus cost of one tile t = $0.7995.
To learn more on equation click:
brainly.com/question/24169758
#SPJ1
On a coordinate plane, (negative 4, 6) is plotted.
Which ordered pair represents the reflection of the point (–4, 6) across both axes?
(4, 6)
(4, –6)
(–4, 6)
(–4, –6)
Answers
The reflection of the point (–4, 6) across both axes is (b) (4, -6)
How to determine the reflection of the point (–4, 6) across both axes?From the question, we have the following parameters that can be used in our computation:
Point = (-4, 6)
The rule of reflections across both axes is
(x, y) = (-x, -y)
Using the above as a guide, we have the following:
Image = (4, -6)
Hence, the reflection of the point (–4, 6) across both axes is (b) (4, -6)
Read more about transformation at
https://brainly.com/question/31898583
#SPJ1
Please help
5x + 3y = 9 in general form.
Answers
jqz-ptqn-jvf
join for your answer and ask
Y intercept =(0,3)
Identify the vertex of each.
2) y = 2x² + 24x + 75
Answers
There would be no x intercepts (I think)
And the y intercept would be (0,7)
So the vertex would be (-6,3)
Find the indicated area under the curve of the standard normal distribution, then convert it to a percentage and fill in the blank. About _____% of the area is between zequalsnegative 2. 2 and zequals2. 2 (or within 2. 2 standard deviations of the mean)
Answers
The area under the curve of the standard normal distribution is 98.61% of the area between equals negative 2. 2 and zequals2. 2
The area under the curve of a standard normal distribution between z = -2.2 and z = 2.2 is given by the integral of the normal distribution function from -2.2 to 2.2. This can be calculated using a table of standard normal probabilities or using a calculator with a normal distribution function.
The result is approximately 0.9861. To convert this to a percentage, simply multiply by 100: 0.9861 * 100 = 98.61%. Therefore, about 98.61% of the area is between z = -2.2 and z = 2.2 (or within 2.2 standard deviations of the mean).
The standard normal distribution is a normal distribution with a mean of 0 and a standard deviation of 1. It is also known as the z-distribution or the unit normal distribution. It is often used in statistical tests, such as the z-test, t-test, and chi-square test. It is also used to determine confidence intervals, to calculate probabilities, and to measure the probability of a given event.
Learn more about standard normal distribution:
https://brainly.com/question/26822684
#SPJ11
What function is represented by the graph? Of(x)=-2|x|+1 Of(x)=-1/2|x|+1 Of(x)=-2|x+1| Of(x)=-1/2|x+1|

Answers
Answer:
f(x)= -2[x+1]
this is the answer of the question
For the trinomial 3x² + 25x +8, choose two numbers whose product is 24 and whose sum is 25.Choose the correct numbers below.
Answers
SOLUTION
From
\(3x^{2}+25x+8\)The two numbers are 24 and 1. Because
\(\begin{gathered} 24\times1=24\text{ and } \\ 24+1=25 \end{gathered}\)Therefore, the two numbers are 24 and 1
PLEASE PLESE HELP ME WITH THIS!!!!

Answers
The new center is 5 units away from the original, hence we added 5 to the x-value.
If you notice the sides of the new triangle are twice the size of the original one, meaning that it was dilated by a scale factor of 2.
4. Compute the unadjusted cost of goods sold for the year. Do not include any underapplied or overapplied overhead in your answer.
5. Assume that the $70,000 ending balance in Work in Process includes $24,000 of direct materials. Given this assumption, supply the information missing below:
Answers
The unadjusted cost of goods sold for the year is calculated by subtracting the ending inventory from the sum of beginning inventory and purchases. The formula is as follows:
Unadjusted Cost of Goods Sold = Beginning Inventory + Purchases - Ending Inventory
Without knowing the values for beginning inventory, purchases, and ending inventory, we cannot compute the unadjusted cost of goods sold for the year.
5. Given that the $70,000 ending balance in Work in Process includes $24,000 of direct materials, we can calculate the missing information as follows:
Direct Labor = Total Work in Process - Direct Materials - Overhead
Direct Labor = $70,000 - $24,000 - Overhead
Without knowing the value for overhead, we cannot compute the direct labor cost. However, we can rearrange the formula to solve for overhead:
Overhead = Total Work in Process - Direct Materials - Direct Labor
Overhead = $70,000 - $24,000 - Direct Labor
Without knowing the value for direct labor, we cannot compute the overhead cost.
https://brainly.com/question/30198250
#SPJ1
A series of books is published at 4-year intervals. When the fifth book is issued, the sum of the publication’s years will be 10,020. When was the first books published?
Answers
Answer:
The first book was published in 1816.
Step-by-step explanation:
A series of books is published at 4-year intervals.
This means that:
The first book is published at year x.
The second book is published at year x + 4.
The third book is published at year x + 4 + 4 = x + 8
The fourth book is published at year x + 8 + 4 = x + 12
The fifth book is published at year x + 12 + 4 = x + 16
When the fifth book is issued, the sum of the publication’s years will be 10,020.
This means that:
\(x + x + 4 + x + 8 + x + 12 + x + 16 = 10020\)
\(5x + 40 = 10020\)
When was the first books published?
This is x. So
\(5x + 40 = 10020\)
\(5x = 9080\)
\(x = \frac{9080}{5}\)
\(x = 1816\)
The first book was published in 1816.
7.8143
whole number what’s is it rounded up to whole number

Answers
The rounded numbers for the given decimal numbers are 4, 8 and 9.
What is rounding a number?To change a number into an approximation having fewer significant digits, is called the rounding numbers.
For example :- Round off 15.4 to 15, round off 15.51 to 15.5 or to 16, round off 0.499 to 0, and round off 970,000 to 1 million.
Given are three decimal numbers, 3.896, 7.8143 and 9.3959 we are asked to round them to whole number.
The rule for rounding the numbers is :-
If the number you are rounding is followed by 5, 6, 7, 8, or 9, round the number up.Example: 38 rounded to the nearest ten is 40.
If the number you are rounding is followed by 0, 1, 2, 3, or 4, round the number down.Example: 33 rounded to the nearest ten is 30.
Therefore, in 3.896, the number after the decimal is 8 which is greater than 5 so rounding up we will get, 4
Similarly, 7.8143 = 8
And in 9.3959, the number after the decimal is 3 which is smaller than 5 so rounding down we will get, 9
Hence, the rounded numbers for the given decimal numbers are 4, 8 and 9.
Learn more about rounding numbers, click;
https://brainly.com/question/5536190
#SPJ9
look at the screenshot x

Answers
Answer:
31.01
Step-by-step explanation:
A= πr^2= π · 3.142 ≈31.01432
Find the equation of this line.1y = x + [?]
![Find the equation of this line.1y = x + [?]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/nDtrkqgoJvSeeb3YNqpbZ91rvBH5GGON.jpeg)
Answers
The equation of the line can be found using the two-point formula:
\(\frac{y_2-y_1}{x_2-x_1}=\frac{y-y_1}{x-x_1}\)From the graph, the intercept points are:
\(\begin{gathered} (x_1,y_1)=(0,-3) \\ (x_2,y_2)=(3,0) \end{gathered}\)Applying the formula,
\(\begin{gathered} \frac{0-(-3)}{3-0}=\frac{y-(-3)}{x-0} \\ \frac{3}{3}=\frac{y+3}{x} \\ 1=\frac{y+3}{x} \\ \text{cross multiply,} \\ y+3=x \\ \text{collect like terms} \\ y=x-3 \end{gathered}\)Therefore, the equation of the line is y = x + [- 3] or y = x - 3