Let f(x)=−2x2+3x−6 and g(x)=5−4x−8x2. Which equation shows h( x), where h(x)=f(x)+g(x)?
h(x)=3x2−x−14
h(x)=6x2+7x−11
h(x)=−10x2−x−1
h(x)=−10x2−7x−11
Answers
Answer:
3rd option
Step-by-step explanation:
(f(x) + g(x)
= - 2x² + 3x - 6 + 5 - 4x - 8x² ← collect like terms
= - 10x² - x - 1
Related Questions
The preference relation ≽ satisfies monotonicity if for all x, y ∈ X, if xk ≥ yk for all k, then x ≽ y, and if xk > yk for all k, then x ≻ y.
The preference relation ≽ satisfies strong monotonicity if for all x, y ∈ X, if xk ≥ yk for all k and x ≠ y then x ≻ y.
Show that preferences represented by min{x1, x2} satisfy monotonicity but not strong monotonicity
Answers
If we contrast the different parts, x1 = 3 2 = y1 and x2 = 4 4 = y2 are the results.
To show that preferences represented by min{x₁, x₂} satisfy monotonicity but not strong monotonicity, we need to demonstrate two things:
Preferences satisfy monotonicity: If xᵢ ≥ yᵢ for all i, then x ≽ y, and if xᵢ > yᵢ for all i, then x ≻ y.
Preferences do not satisfy strong monotonicity: There exist x and y such that xᵢ ≥ yᵢ for all i, but x ≠ y, and x ≰ y.
Let's address each of these points:
Monotonicity:
Suppose x and y are two bundles such that xᵢ ≥ yᵢ for all i. We need to show that x ≽ y and x ≻ y.
First, note that min{x₁, x₂} represents the minimum value between x₁ and x₂, and the same applies to y₁ and y₂.
Since x₁ ≥ y₁ and x₂ ≥ y₂, we can conclude that min{x₁, x₂} ≥ min{y₁, y₂}.
Therefore, x ≽ y, indicating that if all components of x are greater than or equal to the corresponding components of y, then x is weakly preferred to y.
However, if x₁ > y₁ and x₂ > y₂, then min{x₁, x₂} > min{y₁, y₂}. Hence, x ≻ y, indicating that if all components of x are strictly greater than the corresponding components of y, then x is strictly preferred to y.
Thus, preferences represented by min{x₁, x₂} satisfy monotonicity.
Strong Monotonicity:
To show that preferences represented by min{x₁, x₂} do not satisfy strong monotonicity, we need to provide an example of x and y such that xᵢ ≥ yᵢ for all i, but x ≠ y, and x ≰ y.
Consider the following bundles:
x = (3, 4)
y = (2, 4)
In this case, x₁ > y₁ and x₂ = y₂, so x ≻ y.
However,Thus, xᵢ ≥ yᵢ for all i, but x ≠ y, and x ≰ y.If we compare the individual components, x₁ = 3 ≥ 2 = y₁ and x₂ = 4 ≥ 4 = y₂.
Therefore, preferences represented by min{x₁, x₂} satisfy monotonicity but not strong monotonicity.
learn more about contrast from given link
https://brainly.com/question/2477099
#SPJ11
Name 4 points that would form a square with the origin at its center
Answers
The points that would form a square are (2, 2), (2, -2), (-2, 2), (-2, -2)
Naming the points that would form a squareFrom the question, we have the following parameters that can be used in our computation:
Forming a square
As a general rule
A square has equal sides and the angles at the vertices are 90 degrees
Since it must make a point with origin at its center, then the center must be (0, 0)
So, we have the following points (2, 2), (2, -2), (-2, 2), (-2, -2)
Read more about coordianates at
https://brainly.com/question/31617619
#SPJ1
What portion of the population are eligible voters and over the age of 24? one-fourth one-third one-half two-thirds.
Answers
The portion of a population is simply a fraction of the population.
The required parameters are missing.
So, I will solve this question using the following parameters
Population = 600Eligible voters over the age of 24 = 400So, the portion of the population that are eligible voters over the age of 24 is calculated by dividing the number of eligible voters over the age of 24 by the overall population.
So, we have:
\(\mathbf{Portion= \frac{400}{600}}\)
Simplify the fraction
\(\mathbf{Portion= \frac{2}{3}}\)
2/3 means two-third
Hence, the portion of the population that are eligible voters over the age of 24 is two-thirds
Read more about portions and fractions at:
https://brainly.com/question/322203
Answer: Option D, “two-thirds”
Step-by-step explanation:
edge 2022
(7t^5 ) (2t^3 ) simplify
Answers
Answer:
14t^8
Step-by-step explanation:
Answer:
14t^8
Step-by-step explanation:
Find the 10th term of the geometric sequence whose common ratio is
1
and whose first term is 6.
Answers
Answer:
6
Step-by-step explanation:
Use the formula
ar^n-1
where a=6 and r=1
solve this please and tell me how you did it
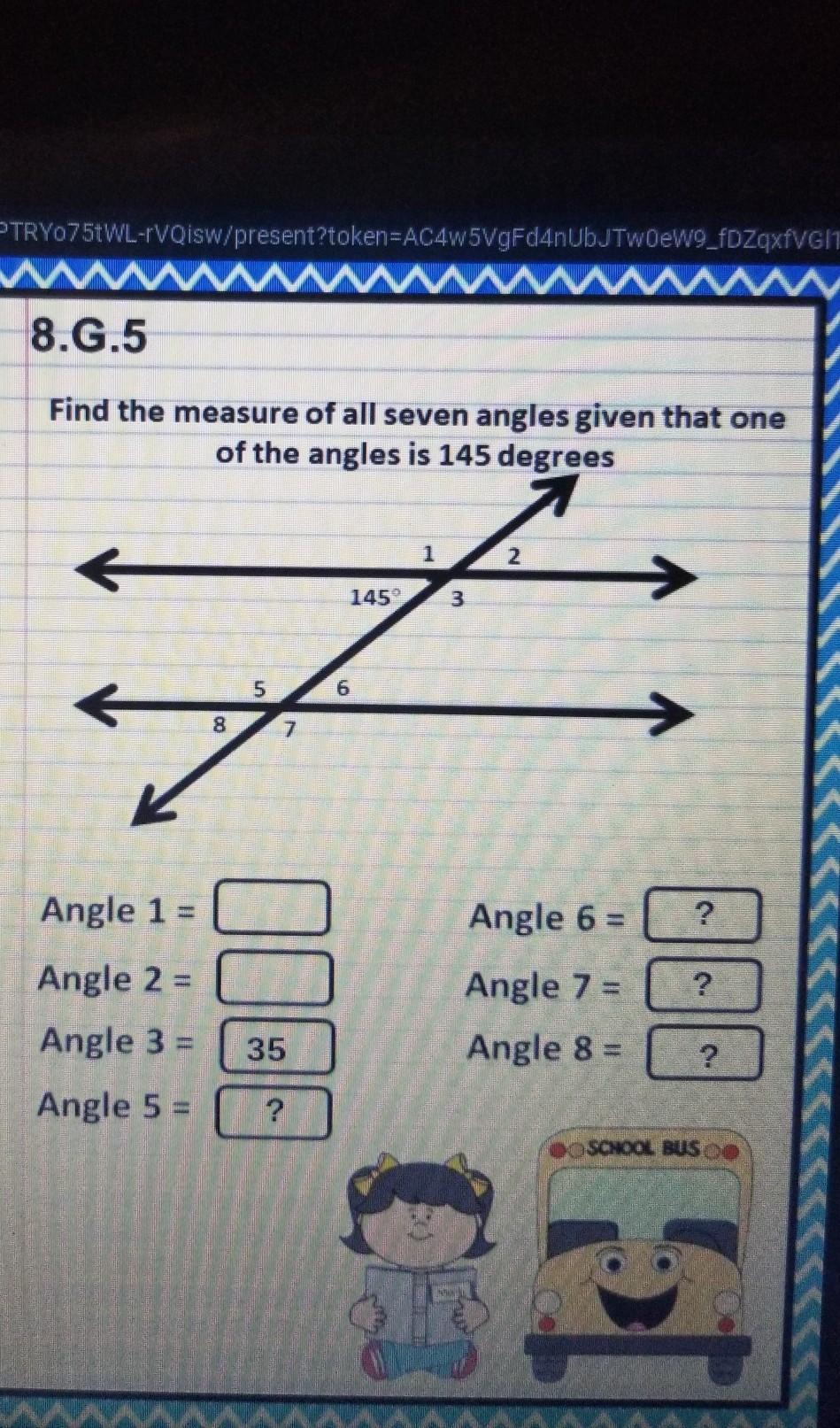
Answers
The angle ∠2 is a vertically opposite angle to the angle 145°, so they are congruent:
∠2 = 145°
The angles 1 and 3 are supplementary angles to the angle 145°, so they are equal to:
180° - 145° = 35°
∠1 = 35°
∠3 = 35°
The angle 8 is a corresponding angle to the angle 145°, so they are congruent:
∠8 = 145°
The angle ∠6 is a vertically opposite angle to the angle ∠8 so they are congruent:
∠6 = 145°
The angles 5 and 7 are supplementary angles to the angle ∠8, so they are equal to:
180° - 145° = 35°
∠5 = 35°
∠7 = 35°
The area of a rectangle is given as x2+5x+6. which expression represents either the length or widith of the rectangle. these are the answers, it has to be one of these (x-3) (x+1) (x+3) (x+6)
Answers
The expression which represents either the length or width is (x+3). The correct answer is option (c).
Given that the area of a rectangle which is given as x²+5x+6.
We have to find which expression represents either the length or width.
We are given an expression for the area. But we also know that the area of a rectangle is length times width. So the expression we were given, x²+5x+6 must be equal to the length of the rectangle times its width.
So, will find the factoring the expression we can see expressions for the length and the width.
Factoring x²+5x+6 we get (x+2)(x+3).
One of these factors is the width and the other is the length.
Hence, the expression represents either the length or width of the rectangle when the area of a rectangle is given as x²+5x+6 is (x+3).
Learn more about the area of rectangle from here brainly.com/questions/2607596
#SPJ4
Maddie has saved $375 for a new mountain bike. Her grandmother will also give her
$215 to help pay for the bike. Which inequality can be used to find p, the price of the
bike that Maddie can afford?
Answers
Answer:
375+215 is greater than or equal to p
Step-by-step explanation:
quick maths
32000 )
bill there
13. Express each of the following recurring decimals as a fraction in its simplest
form
a) 0.8333
b) 0.373737
C) 0.321
Answers
GIVEN: The decimal numbers are given.
TO FIND: We need to find the fractions.
SOLUTION:
a) The decimal form is 0.8333
\(\frac{8333}{10000}\\\)
b)The decimal form is 0.373737
\(\frac{373737}{1000000}\)
c)The decimal form is 0.321
\(\frac{321}{1000}\)
6 divided 5/9 in simplest form ?
Answers
Answer:
If I read your question correctly, then the answer is 54/5.
Step-by-step explanation:
6 ÷ 5/9 Orginial Equation
6/1 x 9/5 Multiply by the Reciprocal
54/5
Please help:) it’s asking for the measure of angle W

Answers
Answer:
10z
Step-by-step explanation:
it shows it on the page
Can someone PLEASE help me? I need help ASAP. It’s due today
Part A: Determine whether a triangle can have side lengths of 5 feet, 9 feet and 15 feet. Show work
Part B: if 2 sides of a triangle are 5 feet and 9 feet, what are possible side lengths for the third side? Show work.
Click on the image to see full view

Answers
Answer:
your formla is \(a{2}\)\(+b{2}=c{2}\) (part A is 5^2 + 9^2) (part B is 106)Mopeds (small motorcycles with an engine capacity below 50 cm3) are very popular in europe because of their mobility, ease of operation, and low cost. suppose the maximum speed of a moped is normally distributed with mean value 46.8 km/h and standard deviation 1.75 km/h. consider randomly selecting a single such moped. a button hyperlink to the salt program that reads: use salt. (a) what is the probability that maximum speed is at most 50 km/h? (round your answer to four decimal places.) ___
(b) what is the probability that maximum speed is at least 49 km/h? (round your answer to four decimal places.) ___
(c) what is the probability that maximum speed differs from the mean value by at most 1.5 standard deviations? (round your answer to four decimal places.) ___
Answers
(a) We need to find P(X ≤ 50), where X is the maximum speed of a moped. We have:
μ = 46.8 km/h
σ = 1.75 km/h
Using standardization, we get:
Z = (X - μ) / σ
Z follows a standard normal distribution. Therefore,
P(X ≤ 50) = P(Z ≤ (50 - μ) / σ)
= P(Z ≤ (50 - 46.8) / 1.75)
= P(Z ≤ 1.8286)
= 0.9641 (rounded to four decimal places)
Therefore, the probability that the maximum speed is at most 50 km/h is 0.9641.
(b) We need to find P(X ≥ 49). Using standardization, we get:
P(X ≥ 49) = P(Z ≥ (49 - μ) / σ)
= P(Z ≥ (49 - 46.8) / 1.75)
= P(Z ≥ 1.2571)
= 0.1038 (rounded to four decimal places)
Therefore, the probability that the maximum speed is at least 49 km/h is 0.1038.
(c) We need to find P(|X - μ| ≤ 1.5σ). Using standardization, we get:
P(|X - μ| ≤ 1.5σ) = P(-1.5 ≤ (X - μ) / σ ≤ 1.5)
= P(-1.5 ≤ Z ≤ 1.5)
= P(Z ≤ 1.5) - P(Z ≤ -1.5)
= 0.8664 - 0.0668
= 0.7996 (rounded to four decimal places)
Therefore, the probability that the maximum speed differs from the mean value by at most 1.5 standard deviations is 0.7996.
Visit here to learn more about probability brainly.com/question/30034780
#SPJ11
please answer these math questions the questions are provided below in the pictures so solve the graphs and put the right answer please.




Answers
1. For Joshua's triangle; the distance of the green side of the triangle d₃ is 5.
2. For Murney's triangle, the perimeter of the triangle is 12.
3. For Grace, Abby and Chris's triangle, the perimeter of the triangle is 5 + √17 + 4√2.
4. For Chloe's triangle, the perimeter of the triangle is 11 + √65.
What is distance of the triangles?
The distance of the triangles is calculated as follows;
For Joshua's triangle;
The length of d₁, d₂, and d₃ is calculated as follows;
d₁ = √ [(3 - 2)² + (2 - 0)²] = √5
d₂ = √ [(-1 - 3)² + (4 - 2)²] = 2√5
d₃ = √ [(-1 - 2)² + (4 - 0)²] = 5
The distance of the green side of the triangle d₃ = 5
For Murney's triangle, the perimeter of the triangle is calculated as;
BC = √ [(4 - 4)² + (6 - 2)²] = 4
AC = √ [(1 - 4)² + (2 - 2)²] = 3
AB = √ [(4 - 1)² + (6 - 2)²] = 5
Perimeter = 4 + 3 + 5 = 12
For Grace, Abby and Chris's triangle, the perimeter of the triangle is calculated as;
AC = √ [(-3 - 2)² + (2-2)²] = 5
BC = √ [(1 - 2)² + (2 + 2)²] = √17
AB = √ [(1 + 3)² + (2 + 2)²] = 4√2
Perimeter = 5 + √17 + 4√2
For Chloe's triangle, the perimeter of the triangle is calculated as;
AC = √ [(-3 - 4)² + (2-2)²] = 7
BC = √ [(4 - 4)² + (6-2)²] = 4
AB = √ [(4 + 3)² + (6-2)²] = √65
Perimeter = 7 + 4 + √65 = 11 + √65
Learn more about perimeter of triangle here: https://brainly.com/question/24382052
#SPJ1
The radius of a circle is 6 feet. What is the circle's circumference? Use 3.14
Answers
Pleaseee helppp answer correctly !!!!!!!!!!!!!! Will mark Brianliest !!!!!!!!!!!!!!!!!!!!

Answers
Answer:
6.324
Step-by-step explanation:
hope i helped you!!
Answer:
6.32
Step-by-step explanation:
d=√(2−8)^2+(−7−(−9))^2
d=√(−6)^2+(2)^2
d=√36+4
d=√40
d=6.324555
D. (-2, 0)
can you plz help
more than one answer

Answers
which of the following best explans why the monopolists marginal revenue is less than the sales price
Answers
Monopolists are firms that have control over the supply of a particular product or service in a market. Due to this control, they can charge higher prices than competitive firms, which can result in lower quantities sold.
One reason why a monopolist's marginal revenue is less than the sales price is due to the downward-sloping demand curve. As the monopolist increases its sales price, the quantity demanded decreases. This means that the revenue generated from each additional unit sold is lower than the revenue generated from the previous unit sold. In other words, the marginal revenue earned from each unit sold is less than the sales price. This occurs because the monopolist must lower the price of all units sold to sell additional units, which lowers the average revenue earned per unit.
To illustrate this, imagine a monopolist that sells widgets for $10 each. If the monopolist lowers the price to $9, it may sell 10 widgets, resulting in revenue of $90 ($9 x 10). However, if the monopolist maintains the $10 price and only sells 9 widgets, the revenue is $90 ($10 x 9). In this case, the marginal revenue for the 9th unit sold is $0, which is less than the sales price of $10. This is because the monopolist must lower the price of all units sold to sell the additional unit, resulting in a decrease in average revenue per unit. Overall, the monopolist's marginal revenue is less than the sales price due to the downward-sloping demand curve and the need to lower prices to sell additional units.
A monopolist, unlike firms in a competitive market, has significant market power due to the absence of competition. This allows the monopolist to control the market price of their product by adjusting the quantity supplied. When a monopolist wants to sell an additional unit, they must lower the sales price for all units, including the ones already being sold. This is because the demand curve faced by a monopolist is downward-sloping, meaning that in order to sell more units, the monopolist has to decrease the price.
Marginal revenue refers to the additional revenue gained from selling one more unit of the product. As the monopolist lowers the sales price to sell more units, two things happen: the revenue increases from the additional unit sold, but there is also a loss in revenue from the units that were sold at a higher price before the price reduction.
As a result, the marginal revenue is less than the sales price, since it takes into account not only the revenue from the additional unit sold but also the loss of revenue from lowering the price of all units. This relationship between the monopolist's pricing strategy and marginal revenue is a key factor in determining the monopolist's profit-maximizing level of output and price.
Learn more about price at : brainly.com/question/18117910
#SPJ11
The equations in this sytem were added to solve for x. What is the value of x?
Negative 2 x + y = 8. 5 x minus y = negative 5. 3 x = 3.
x = negative 3
x = negative 1
x = 1
x = 3
Answers
The value of x would be 1.
determine a region whose area is equal to the given limit. do not evaluate the limit.
Answers
The obtained limit is identical to the limit that was specified. Therefore, the right answer is option C.
What is a region whose area is equal to the given limit?Generally, the equation for the limit is mathematically given as
\($\lim _{n \rightarrow \infty} \sum_{i=1}^{n} \frac{4}{n} \sqrt{1+\frac{4 i}{n}}$.\)
The goal is to locate the zone whose area corresponds to the value supplied by the limit.
The definite integral of a function is what is used to compute the area of that function that is underneath its graph.
The limit,
\(\lim _{n \rightarrow \infty} \sum_{i=1}^{n} f(a+i \cdot \Delta x) \Delta x\)
where\($\Delta x=\frac{b-a}{n}$\) and \($x_{i}=a+i \Delta x$\) for the interval $[a, b]$, is equivalent to the integral
\(\int_{a}^{b} f(x) d x .\)
The given limit can also be written as
\(\lim _{n \rightarrow \infty} \sum_{i=1}^{n} \sqrt{1+\left(\frac{4}{n}\right)} i \cdot \frac{4}{n} .\)
In this limit, \($\Delta x=\frac{4}{n}$\). It can be observed that\($f(a+i \Delta x)=\sqrt{1+\left(\frac{4}{n}\right)} i$\) which implies that \($a=1$ and $f(x)=\sqrt{x}$.\)
Solve the \($\Delta x=\frac{b-a}{n}$\)equation for as follows:
\(\begin{aligned}\frac{4}{n} &=\frac{b-1}{n} \\4 &=b-1 \\5 &=b\end{aligned}\)
Therefore, the specified limit may be expressed as an integral as follows:
\(\lim _{n \rightarrow \infty} \sum_{i=1}^{n} \sqrt{1+\left(\frac{4}{n}\right) i} \cdot \frac{4}{n}=\int_{1}^{5} \sqrt{x} d x\)
Therefore, the limit that has been provided designates the area of the graph of "sqrt(x)" on the interval.[1,5]
However, none of the available choices are compatible with this choice. So, consider
\(a=0, f(x)=\sqrt{1+x}$ and $\Delta x=\frac{4}{n}$.\)
Find the value of $b$ as:
\($$\begin{aligned}\frac{4}{n} &=\frac{b-0}{n} \\4 &=b\end{aligned}$$\)
Find the value of x_{i} as:
\(\begin{aligned}&x_{i}=0+\frac{4}{n} i \\&x_{i}=\frac{4}{n} i\end{aligned}\)
$$
Thus, the integral \($\int_{0}^{4} \sqrt{1+x} d x$\) can be expressed using the equation \($\int_{a}^{b} f(x) d x=\lim _{n \rightarrow \infty} \sum_{i=1}^{n} f\left(x_{i}\right) \Delta x$\)
\(\begin{aligned}\int_{0}^{4} \sqrt{1+x} d x &=\lim _{n \rightarrow \infty} \sum_{i=1}^{n} \sqrt{1+\frac{4 i}{n} \frac{4}{n}} \\&=\lim _{n \rightarrow \infty} \sum_{i=1}^{n} \frac{4}{n} \sqrt{1+\frac{4 i}{n}}\end{aligned}\)
In conclusion, The obtained limit is identical to the limit that was specified. Therefore, the right answer is option C.
Read more about region
https://brainly.com/question/13162113
#SPJ4
CQ
The complete Question is attached below

Solve the quadratic using the quadratic formula. *
Solve:
6x^2 + 7x – 5 = 0
Answers
Answer:x = -5/3 or x = 1/2
Step-by-step explanation:
Let's solve your equation step-by-step.
6x2+7x−5=0
Step 1: Factor left side of equation.
(3x+5)(2x−1)=0
Step 2: Set factors equal to 0.
3x+5 = 0 or 2x−1 = 0
x = -5/3 or x = 1/2
Answer:
\(x=\frac{1}{2}\)
\(x=-1\frac{2}{3}\)
Step-by-step explanation:
\(x=\frac{-b±\sqrt{b^{2} +4ac} }{2a}\)
Ignore the A before the ±, it wouldn't let me type it correctly.
6x² + 7x - 5 = 0
a = 6
b = 7
c = - 7
\(x=\frac{-(7)±\sqrt{7^{2} +4((6)(-5))} }{2(6)}\)
\(x=\frac{-(7)±\sqrt{49 +4((6)(-5))} }{2(6)}\)
\(x=\frac{-(7)±\sqrt{49 +120} }{2(6)}\)
\(x=\frac{-7±\sqrt{169} }{12}\)
\(x=\frac{-7±13 }{12}\)
Two separate equations
\(x=\frac{-7+13 }{12}\)
\(x=\frac{-7-13 }{12}\)
________________________
\(x=\frac{-7+13 }{12}\)
\(x=\frac{6 }{12}\)
\(x=\frac{1}{2}\)
\(x=\frac{-7-13 }{12}\)
\(x=\frac{-20 }{12}\)
\(x=-1\frac{2}{3}\)
The wire supporting a 20-foot tall phone pole is attached to the top of the pole, and to the
ground 12 feet from the pole. How long is the wire?
Answers
Answer:
22.36 feet
Step-by-step explanation:
This situation forms a right triangle, where the wire is the hypotenuse
Use the pythagorean theorem to find the hypotenuse/wire length:
a² + b² = c²
20² + 12² = c²
400 + 144 = c²
544 = c²
22.36 = c
So, the wire is 22.36 feet long
What is the best first step to solve the following quadratic equation?
16x2 + 38 = -40x
A
Add 40x to both sides.
B
Factor the right side.
C
Take the square root of both sides.
D
Multiply 16 by 38 and list the factors.
Answers
Answer:
a
Step-by-step explanation:
A which is add 40x to both sides wich is A
Which quantity makes the equation true?
x + 3x + _______ = 7x

Answers
Answer:
Step-by-step explanation:
C) 3X
Answer: C. 3x
Step-by-step explanation:
Since x and 3x both have x, you can add them together to get 4x (if there is x by itself, it really means that there is one of it, so it would be 1x.)
Then, you subtract 7x by 4x, which gives you the answer, 3x. You could also solving it by asking yourself: What number plus 4x equals 7x, which would give you 3x.
What does y equal?
Will Give Brianlest!

Answers
Answer:
\(\boxed{\tt y=48}\)
Step-by-step explanation:
\(\tt \cfrac{3}{16}=\cfrac{9}{y}\)
Cross multiply:-
\(\tt 3 \times y=(9)\times (16)\)
\(\tt 3y=144\)
Divide both sides by 3:-
\(\tt \cfrac{3y}{3}=\cfrac{144}{3}\)
Simplify:-
\(\tt y=48\)
_________________
Hope this helps!
Answer:y=48 I hope this is helpful good luck have a good day
Step-by-step explanation:
3/16 = 9/y
Determine the defined range
3/16=9/y y=0 cross out the equal sign y=0
Simplify the equation using cross-multiplication
3y=144
Divide both sides of the equation by 3
y=48
Check if the solution is in the defined range
Arianys runs a farm stand that sells grapes and apples. Each pound of grapes sells for
$3.75 and each pound of apples sells for $4. Arianys made $251.75 from selling a
total of 64 pounds of grapes and apples. Determine the number of pounds of grapes
sold and the number of pounds of apples sold.
Answers
The number of pounds of grapes is 24 sold and the number of pounds of apples sold is 30.
Given that,
Apples and grapes are sold at Arianys' farm stand. The price per pound for apples is $4 while the price per pound for grapes is $3.75. 64 pounds of apples and grapes were sold for a total profit of $251.75 for Arianys.
We have to find the number of the sold apples and pounds of grapes should be calculated.
What are the equation?a declaration that two mathematical expressions' values are equal (represented by the symbol =).
We get the equations as,
3.75x+4y=251.75
y=-0.93x+62.93---->equation(1)
x+y=64
y=-x+64------>equation (2)
We get the points as
For equation (1),
(0,62.93) and (67.66,0)
For equation (2),
(0, 64) and (64,0)
If we draw a graph we get 2 lines intersect at a point (24, 30).
Therefore, The number of pounds of grapes is 24 sold and the number of pounds of apples sold is 30.
To learn more about number visit: https://brainly.com/question/17429689
#SPJ13
How do you find the midpoint of coordinates
Answers
Answer:
The midpoint is halfway between two end points.
The x value is halfway between the two x values and
the y value is also halfway between the two y values.
Add both the x and y coordinates and divide by 2.
Step-by-step explanation:
To find the x-coordinate of the midpoint of a segment, add the x-coordinates of the endpoints and divide by 2.
To find the y-coordinate of the midpoint of a segment, add the y-coordinates of the endpoints and divide by 2.
Example:
Find the midpoint of the segment with endpoints (2, 8) and (-5, 12).
x-coordinate of the midpoint: (2 + (-5))/2 = -3/2
y-coordinate: (8 + 12)/2 = 30/2 = 15
Midpoint: (-3/2, 15)
Algebra 2 :1-16
Please help meee

Answers
Answer:
not sure lol
Step-by-step explanation:
1: 25i
2: 19a
Question 1.
in exploration 5.1.1 question 2, you identified the y-intercept as (0, a) and the
horizontal asymptote as y= b, where
a=
b=
Answers
a=b, The curve approaches the line y=a as x approaches infinity or negative infinity.
since the y-intercept is the point where the curve intersects the y-axis, i.e., x=0.
Since we have (0, a) as our y-intercept, then a=b, where a and b are constants.
The y-intercept, as indicated in the question, is (0, a) meaning that for the function f(x), when x=0, then f(x) = a.
The horizontal asymptote of a function is a horizontal line that the graph approaches as x approaches infinity or
negative infinity.
If the horizontal asymptote is y=b, it means that the value of y approaches b as x approaches infinity or negative infinity.
Therefore, since a=b, the curve approaches the line y=a as x approaches infinity or negative infinity.
for such more question on curve
https://brainly.com/question/26460726
#SPJ11
The diameter of a hydrogen atom is about 1.05 cross times 10 to the power of negative 10 end exponentmeters. a protein molecule has an overall length of 3000 times (or 3 cross times 10 cubed times) the diameter of a hydrogen atom. what is the length of the protein molecule, in meters, if it were written in scientific notation?
Answers
The length of the protein molecule, in meters, is 208 × 10⁻⁹m.
What is an atom?An atom is a matter particle that defines a chemical element uniquely. An atom is made up of a central nucleus and one or more negatively charged electrons. The nucleus is positively charged and contains one or more protons and neutrons, which are relatively heavy particles.To find the length of the protein molecule:
Diameter of hydrogen atom = 104 × 10⁻¹⁰m
We are given that A protein molecule has an overall length of 2000 times (or 2 cross times 10 cubed times) the diameter of a hydrogen atom.
Length of protein molecule = 2000 × Diameter of the hydrogen atomLength of protein molecule = 2 × 10⁺³ × 1.04 × 10⁻¹⁰Length of protein molecule = 2 × 1.04 × 10⁻¹⁰⁺³Length of protein molecule = 2 × 1.04 × 10⁻⁷Length of protein molecule = 2.08 × 10⁻⁷Length of protein molecule = 208 × 10⁻⁷⁻²Length of protein molecule = 208 × 10⁻⁹mTherefore, the length of the protein molecule, in meters, is 208 × 10⁻⁹m.
Know more about atoms here:
https://brainly.com/question/6258301
#SPJ4
The correct question is given below:
The diameter of a hydrogen atom is about 1.04 cross times 10 to the power of negative 10 end exponent meters. A protein molecule has an overall length of 2000 times (or 2 cross times 10 cubed times) the diameter of a hydrogen atom. What is the length of the protein molecule, in meters, if it were written in scientific notation?