Last minute please help me out !!!
Find a polynomial expression in terms of x for the volume of the rectangular prism shown.

Answers
Answer:
V = 6x³ - 21x² - 12x
Step-by-step explanation:
Volume of a Rectangular Prism: V = lwh
Step 1: Define
l = 3x
w = x - 4
h = 2x + 1
Step 2: Substitute
V = 3x(x - 4)(2x + 1)
Step 3: Expand
V = 3x(2x² - 7x - 4)
V = 6x³ - 21x² - 12x
Answer:
6x to the power of 3 + x to the power of 2 - 4
Related Questions
employees at an arcade are paid according to the number of hours worked as shown in the graph

Answers
Answer:
B, C, G
Step-by-step explanation:
If we look at the graph, it shows that if an employee works for 5 hours, then they will earn $36.25.
We can take 36.25 and divide that by 5 to get the hourly wage.
36.25 ÷ 5 = 7.25
We now know that employees get $7.25 every hour.
Using this we can look back to the graph.
'A' says that if an employee does not work, they will earn $7.25.
We know that this is wrong because if you do not work, then you do not earn money.
Let's look at 'B'.
If employees work for one hour, they will earn $7.25
We know this is correct because we now know the hourly wage.
Let's look at 'C'
If employees work for 4 hours, then they will get a revenue of $29.
We can figure this out by using this equation.
number of hours × hourly wage = total payment
4 × 7.25 = 29
Then this means that this is correct.
Let's look at 'D'
It says that if employees work for 10 hours, they will earn $73
Let's use that same equation again.
10 × 7.25 = 72.5
Employees earn $72.5 for working 10 hours, not $73.
So, this is obviously incorrect.
Let's look at 'E'
It says that if employees work for 3.5 hours, they will get a revenue of $21.75.
3.5 × 7.25 = 25.375
Therefore, this is incorrect.
Now let's take a look at 'F'.
It says that if employees work for 7.25 hours, then they earn $1.
This is incorrect.
And lastly, 'G'.
We know that if you do not work, then you do not earn money.
Therefore, A, B and G are the correct answers.
Find the simplified product 5/n+1 x n+1/n+3

Answers
Cancel out common factor
Final answer: 5/n+3
Answer: C) 5/n+3
Step-by-step explanation:
a statement with the greatest acceptance among scientists is the______
Answers
Help Please!!!
That partitions the segments into a ratio of 3 to 2

Answers
let's say the segment with A(-5 , -8) and B(10 , 7) gets partitioned by point C
\(\textit{internal division of a line segment using ratios} \\\\\\ A(-5,-8)\qquad B(10,7)\qquad \qquad \stackrel{\textit{ratio from A to B}}{3:2} \\\\\\ \cfrac{A\underline{C}}{\underline{C} B} = \cfrac{3}{2}\implies \cfrac{A}{B} = \cfrac{3}{2}\implies 2A=3B\implies 2(-5,-8)=3(10,7)\)
\((\stackrel{x}{-10}~~,~~ \stackrel{y}{-16})=(\stackrel{x}{30}~~,~~ \stackrel{y}{21}) \implies C=\underset{\textit{sum of the ratios}}{\left( \cfrac{\stackrel{\textit{sum of x's}}{-10 +30}}{3+2}~~,~~\cfrac{\stackrel{\textit{sum of y's}}{-16 +21}}{3+2} \right)} \\\\\\ C=\left( \cfrac{ 20 }{ 5 }~~,~~\cfrac{ 5}{ 5 } \right)\implies C=(4~~,~~1)\)
Answer:
( 4, 1 )
Step-by-step explanation:

Anne bought a piece of ribbon that is 7 over 9 m long. She used 3 over 18 m of it to tie a birthday present. She then used the remaining ribbon to form squares of sides 1 over 16 m. What was the maximum number of squares she could form?
Answers
Answer:
9 squares
Step-by-step explanation:
Anne bought a piece of ribbon = 7 over 9 m long = 63 m²
she used = 3 over 18 m = 54 m²
left = 9 m²
maximum number of squares she could form of 1 m = 9
Solve the system of linear equations using substitution. Use a pencil and paper. Which expression would be easier to substitute into the other equation, in order to solve this problem? Explain your reasoning.
x=4y-9
x+4y=3
Answers
Answer:
(- 3, 1.5)
--------------------------
Given system:
x = 4y - 9x + 4y = 3The first expression is ready to be substituted as no further operation is required to simplify it.
4y - 9 + 4y = 38y - 9 = 38y = 12y = 12/8y = 1.5Find x:
x = 4*1.5 - 9x = 6 - 9x = - 3Helppppppppppppppppppppp!!!!!!!!

Answers
Because of some theory with angles on same sides of a line between parallel lines, take 180 and subtract the ones you have. 180-107=73 degrees= m angle B
180-46=134 degrees - m angle A
Please see the attached.

Answers
Answer:
min: 56
lower quartile: 70
median: 74
upper quartile: 80
max: 86
Which number completes the inequality?
2/3<_<7/9
Group of answer choices
69
34
67
35
Answers
Answer:
it is 3/4
Step-by-step explanation:
I got it right no my test
r negative 7 divided by s negative 1
Answers
Unfortunately that's an impossible question because we have no idea what the variable is. Sorry buddy. You're on ur own there
3 x (x+y) -4(2) for x=6 and y=4
Answers
Answer: 22
Step-by-step explanation:
3 x (6+4) -4(2) (substitute x=6 and y=4)
= 3 x 10 - 8 (simplify inside the parentheses)
= 30 - 8 (multiply)
= 22 (subtract)
Therefore, 3 x (x+y) -4(2) is equal to 22 when x=6 and y=4.
It is known that 1.4< square root of 2 <1.5. Find all possible values of the expression 2-square root of 2. How do I find out the second inequality?
Answers
Answer:
0.5<2-√2<0.6
Step-by-step explanation:
The original inequality states that 1.4<√2<1.5
For the second inequality, you can think of 2-√2 as 2+(-√2).
Because of the "properties of inequalities", we know that when a positive inequality is being turned into a negative, the numbers need to swap and become negative. So, the original inequality becomes -1.5<-√2<-1.4. (Notice how the √2 becomes negative, too). This makes sense because -1.5 is less than -1.4.
Using our new inequality, we can solve the problem. Instead of 2+(-√2), we are going to switch "-√2" with both possibilities of -1.5 and -1.6. For -1.5, we would get 2+(-1.5), or 0.5. For -1.4, we would get 2+(-1.4), or 0.6.
Now, we insert the new numbers into the equation _<2-√2<_. The 0.5 would take the original equation's "1.4" place, and 0.6 would take 1.5's. In the end, you'd get 0.5<2-√2<0.6. All possible values of 2-√2 would be between 0.5 and 0.6.
Hope this helped!
The possible values of 2-√2 will be in the range is 0.6 > 2 -√2 > 0.5.
What is inequality?Inequality is defined as mathematical statements that have a minimum of two terms containing variables or numbers that are not equal.
What are Arithmetic operations?Arithmetic operations can also be specified by the subtract, divide, and multiply built-in functions.
* Multiplication operation: Multiplies values on either side of the operator
For example 4*2 = 8
We have the given statement that 1.4 < √2 < 1.5
We have to determine the possible values of 2-√2 as 2+(-√2).
According to the question,
⇒ 1.4 < √2 < 1.5
Multiply by a minus sign (-) in the inequality
⇒ -1.4 > -√2 > -1.5
Adding 2 in the inequality
⇒ 2-1.4 > 2 -√2 > 2-1.5
⇒ 0.6 > 2 -√2 > 0.5
Hence, the possible values of 2-√2 will be in the range is 0.6 > 2 -√2 > 0.5.
Learn more about the inequalities here:
brainly.com/question/20383699
#SPJ2
SOMEONE PLEASE ANSWER. I'M CRYING AND DONT KNOW WHAT TO DO! I NEED YOUR HELP PLEASE!
A cafeteria serves lemonade that is made from a powdered drink mix. There is a proportional relationship between the number of scoops of powdered drink mix and the amount of water needed to make it. For every 2 scoops of mix, one half gallon of water is needed, and for every 5 scoops of mix, one and one fourth gallons of water are needed. Part A: Find the constant of proportionality. Show every step of your work. Part B: Write an equation that represents the relationship. Show every step of your work. Part C: Describe how you would graph the relationship. Use complete sentences. Part D: How many gallons of water are needed for 12 scoops of drink mix?
Answers
Below, you'll find a list of all the answers to the questions which are solved by using proportional relationship.
What is the fundamental formula for a straight line?The general equation for a straight line is y=mx + c, where m represents the line's slope and expresses the rate of change of y per unit time with respect to x.
The point where the graph crosses the y-axis is called the y-intercept, or c.
Direct proportionality is also represented by y = mx. We can express m as follows: m = y/x
OR
y₁/x₁ = y₂/x₂
In our cafeteria, lemonade is made using a powdered drink mix. The quantity of water required to manufacture a certain amount of powdered drink mix is proportional to the number of scoops required. For every 2 scoops of mix, 1/2 gallon of water is required, and for every 5 scoops,
1 1/4 gallons of water are required.
The proportional formula is written as y = k x.
Using the information provided, we can now write: 2 scoops require 0.5 gallon of water.
1.25 gallon of water is required for 6 scoops.
This means that k = 2/0.5
k = 2/(1/2)
k = 2 x 2
k= 4
Equations describing the relationship can be expressed as y = 4x + c.
0.5 gallon of water is now required for 2 scoops.
2=4(1/2)+c
2=2+c
c=0
Therefore, the formula will be y = 4x.
The end includes a graph for y = 4x.
12 scoops of water:
12=4x
x=3 gallons of water is needed.
To know more about proportional relationship, visit:
https://brainly.com/question/29765554
#SPJ1

What is the value of the expression below when w=2

Answers
Answer:
26
Step-by-step explanation:
8 * 2 + 10 = 26
) Quantifier negation.
Form the negation of the following statements. Then apply De Morgan’s law and/or conditional law, when
applicable. Negation should appear only within predicates, i.e., no negation should be outside a quantifier
or an expression involving logical connectives. Show all steps.
a) ∀x (P(x) ∧ R(x))
b) ∀y∃z(¬P(y) → Q(z))
c) ∃x (P(x) ∨ (∀z (¬R(z) → ¬Q(z))))
Answers
The negations of the given statements with the application of De Morgan's law and/or conditional law.
a) ∃x (¬P(x) ∨ ¬R(x))
De Morgan's law:
∃y ∀z(¬P(y) ∧ ¬Q(z))
b) ∃y ∀z(¬P(y) ∧ ¬Q(z))
The double negation:
∃y ¬∃z(P(y) ∨ Q(z))
c) ¬∃x (P(x) ∨ (∀z (¬R(z)) → (∀z ¬Q(z))))
The conditional law:
¬∃x (P(x) ∨ (∀z (¬R(z)) → (∀z ¬Q(z))))
Let's form the negation of the given statements and apply De Morgan's law and/or conditional law, when applicable:
a) ∀x (P(x) ∧ R(x))
The negation of this statement is:
∃x ¬(P(x) ∧ R(x))
Now let's apply De Morgan's law:
∃x (¬P(x) ∨ ¬R(x))
b) ∀y∃z(¬P(y) → Q(z))
The negation of this statement is:
∃y ¬∃z(¬P(y) → Q(z))
Using the conditional law, we can rewrite the negation as:
∃y ¬∃z(¬¬P(y) ∨ Q(z))
c) ∃x (P(x) ∨ (∀z (¬R(z) → ¬Q(z))))
The negation of this statement is:
¬∃x (P(x) ∨ (∀z (¬R(z) → ¬Q(z))))
Using the conditional law, we can rewrite the negation as:
¬∃x (P(x) ∨ (∀z (R(z) ∨ ¬Q(z))))
Applying De Morgan's law:
¬∃x (P(x) ∨ (∀z ¬(¬R(z) ∧ Q(z))))
Simplifying the double negation:
¬∃x (P(x) ∨ (∀z ¬(R(z) ∧ Q(z))))
Using De Morgan's law again:
¬∃x (P(x) ∨ (∀z (¬R(z) ∨ ¬Q(z))))
For similar questions on De Morgan's law
https://brainly.com/question/28735989
#SPJ8
to determine whether families with children would use school vouchers to send their children to charter schools, from which of the following populations should you select a sample?
Answers
Parents of children under the age of 18.
It is seldom feasible to get data from every member of a group of individuals when conducting research on them. In its place, you pick a sample. The population that will actually take part in the study is the sample. It is referred to as a sampling method. You can use one of the following two main sampling techniques in your study:
Random selection is a key component of probability sampling, which enables you to draw robust statistical conclusions about the entire group.
Non-probability sampling entails non-random selection based on practicality or other factors, making it simple to gather data.
To know more about sampling visit: brainly.com/question/13287171
#SPJ4
square root of the quantity x plus 7 end quantity minus 11 equals 2
Answers
An equation is formed when two equal expressions are equated together. The value of x in the equation [√(x+7)]-11=2 is 162.
What is an equation?An equation is formed when two equal expressions are equated together with the help of an equal sign '='.
The solution for x in the equation [√(x+7)]-11=2 can be solved as,
\(\sqrt{x+7}-11=2\\\)
Using the addition property of equality,
\(\sqrt{x+7} -11+11= 2+11\\\\\\\sqrt{x+7} = 13\)
Squaring both the sides of the equation,
x + 7 = 169
Using the subtraction property of equality,
x + 7 - 7 = 169 - 7
x = 162
Hence, the value of x in the equation [√(x+7)]-11=2 is 162.
Learn more about Equation:
https://brainly.com/question/2263981
#SPJ1
Calculate the federal income taxes. In 1980, the federal income tax was 14 percent on incomes between $2,300 and $3,400 per year, 16 percent
on incomes between $3,400 and $4,400 per year, and 21 percent on incomes between $8,500 and 10,800 per year. In 1980, you made $3,000.
What was your income tax this year?
O $42.00
O $420
$480
$630
Answers
Answer: 420
Step-by-step explanation: 14 percent of 3000 is 420
Correct Answer: $420

Which is the asymptote of the graph?

Answers
Answer:
You have it y=-1
Step-by-step explanation:
It's hard to explain
Find the slope of the line
Slope=m=_____
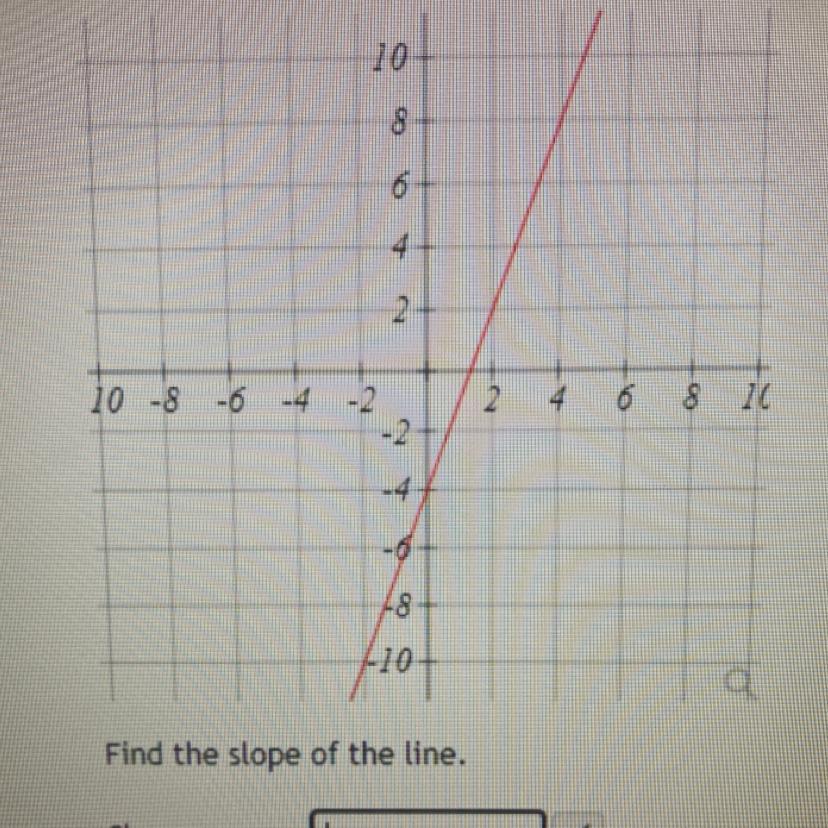
Answers
Answer:
4
Step-by-step explanation:
Slope = y2-y1/x2-x1
We need to find two points on the graph, let's take these two points:
(x1, y1) (X2,y2)
(0,-6) and (2,2)
(2-(-6)/ (2-0) = 8/2 = 4
Answered by Gauthmath
Which graph represents this system of equations?
y + 2x = 3
y + 2 = 3x
Answers
Answer:
The options are not given, so i will answer in a general way.
First, we have the system:
y + 2*x = 3
y + 2 = 3*x
To graph this system, the easier way is writing both equations as linear equations, like:
y = -2*x + 3
y = 3*x - 2
Now we just need to graph these two lines in the same coordinate axis.
To do it, we can replace the value of x by two different values in each equation, and see the correspondent value of y for these values. Then graph the two points, and draw a line that connects them.
For example, for the first equation if we have x = 0, we have:
y = -2*0 + 3
y = 3
Then we have the point (0, 3)
and if x = 1
y = -2*1 + 3 = 1
y = 1
we have the point (1, 1)
Now we only need to graph these points, and draw a line that passes through them.
Once we did this for both lines, the graph we will get will look something like the one above.
And the point where the lines intersect is the solution of the system of equations.
Which is the point (1, 1)

Please help, Which statements about the graph are true? Choose all the true statements.
A.) The friends stopped for a break between hours 3 and 4.
B.) The friends hiked at a constant speed for the first 2 hours.
C.) The friends hiked at the maximum speed for 7 and 8.
D.) The friends hiked the least number of miles between hours 6 and 7.
E.) The friends hiked back toward the starting point between hours 3 and 4.

Answers
Answer:
I would say it's C
Step-by-step explanation:
trust the process
A box plot is shown
O
2
4
6
8
10
12
Determine the five-statistical summary of the data. Drag the correct number to each variable in the summary.
14
16
18
20
22 24 26
28
30
Minimum:
Maximum:
Median:
First Quartile:
Third Quartile:
1
2
3
4
11
5
12
6
ما تا ته
13
14
8
21
15
22
16
10
23
17
24
18
25
19
26
20
27
28
29
30
Please answer fast

Answers
Answer:
Minimum = 8
Maximum = 28
Median = 22
First Quartile = 12
Third Quartile = 26
Step-by-step explanation:
✔️Minimum value = the value at the beginning of the whisker from your left = 8
✔️Maximum value = the value at the end of the whisker to your right = 28
✔️Median = the value at the vertical line that divides the box into two = 22
✔️First Quartile = the value at the beginning of the edge of the box = 12
✔️Third Quartile = the value at end of the edge of the box = 26
what is the square root of 114 as a decimal to the hundredths place?
Answers
Answer:
0.012
Step-by-step explanation:
Answer:
10.67707825
Step-by-step explanation:
that should be the correct answer
1. The tiles shown are placed in a bag. You randomly select one of the tiles,
return it to the bag, and then randomly select another tile. What is the
probability that the first number divided by the second number is greater
than zero?
the numbers:
-2
-1
2
1
Answers
Therefore, the probability that the first number divided by the second number is greater than zero is 1/3.
What is probability?In mathematics, probability is a measure of the likelihood or chance of an event occurring. It is a way of quantifying uncertainty and expressing how likely it is that a particular outcome will occur. Probability theory is used in a wide range of fields, including mathematics, statistics, physics, engineering, economics, and social sciences. It is used to model and analyze random phenomena, make predictions, and estimate the likelihood of certain outcomes.
Here,
Since we are returning the first tile to the bag before selecting the second one, the two selections are independent of each other.
There are two cases to consider:
Case 1: We select a positive number on the first draw.
The probability of selecting a positive number on the first draw is 2/3, since there are two positive numbers (-12 and 1) out of a total of three tiles.
Regardless of what number we select on the first draw, there is only one negative number (-2) in the bag, so the probability of selecting a negative number on the second draw is 1/3.
Therefore, the probability of selecting a positive number on the first draw and a negative number on the second draw (which results in a quotient greater than zero) is:
(2/3) x (1/3) = 2/9
Case 2: We select the negative number (-2) on the first draw.
The probability of selecting the negative number (-2) on the first draw is 1/3.
In this case, we must select the positive number on the second draw in order for the quotient to be greater than zero. There is only one positive number (1) in the bag, so the probability of selecting it on the second draw is 1/3.
Therefore, the probability of selecting the negative number (-2) on the first draw and the positive number on the second draw (which results in a quotient greater than zero) is:
(1/3) x (1/3) = 1/9
Since these are the only two cases that satisfy the condition, the overall probability is the sum of the probabilities of these two cases:
2/9 + 1/9 = 3/9 = 1/3
To know more about probability,
https://brainly.com/question/30034780
#SPJ1
The distance from the tip of a slice of pizza to the crust is 7 inches.
Does this represent diameter, circumference, or radius?
ANSWER ASAP THANK YOU
Answers
Answer:
radius
Step-by-step explanation:
There are 6 acts in a talent show.
An acrobat, a dancer, a guitarist, a singer, a violinist, and a whistler.
A talent show host randomly schedules the 6 acts.
Compute the probability of each of the following events.
Event A: The acrobat is first, the singer is second, the violinist is third, and the whistler is fourth.
Event B: The first four acts are the whistler, the acrobat, the guitarist, and the dancer, In any order.
Write your answers as fractions in simplest form.
P(A) =
P (B) =
Answers
The probability of Event A is 1/360 and the probability of Event B is 1/15.
For Event A, we can calculate the probability by considering the order in which the acts are scheduled.
There are 6 acts, so there are 6 possible choices for the first act. After the first act is scheduled, there are 5 remaining acts, so there are 5 possible choices for the second act.
Similarly, there are 4 possible choices for the third act, and 3 possible choices for the fourth act.
Finally, there are 2 possible choices for the fifth act, and only 1 choice remains for the last act.
Therefore, the total number of possible ways to schedule all 6 acts is:
6 x 5 x 4 x 3 x 2 x 1 = 720
Since we are only interested in one specific order of the first four acts, we need to count the number of ways to schedule the remaining two acts after the first four have been scheduled in the desired order.
There are 2 remaining acts, so there are 2 possible choices for the fifth act.
Only one act remains for the last slot.
Therefore, the total number of ways to schedule all 6 acts such that the acrobat is first, the singer is second, the violinist is third, and the whistler is fourth is:
1 x 1 x 1 x 1 x 2 x 1 = 2
Thus, the probability of Event A is:
P(A) = 2/720 = 1/360
For Event B, we want to count the number of ways to schedule the first four acts as the whistler, the acrobat, the guitarist, and the dancer, in any order.
There are 4 acts, so there are 4 possible choices for the first act. After the first act is scheduled, there are 3 remaining acts, so there are 3 possible choices for the second act.
Similarly, there are 2 possible choices for the third act, and only one choice remains for the fourth act.
Therefore, the total number of possible ways to schedule the first four acts is:
4 x 3 x 2 x 1 = 24
Since we do not care about the order in which the last two acts are scheduled, we can simply choose any two acts from the remaining 2. There are 2 ways to do this.
Therefore, the total number of ways to schedule all 6 acts such that the first four acts are the whistler, the acrobat, the guitarist, and the dancer, in any order is:
24 x 2 = 48
Thus, the probability of Event B is:
P(B) = 48/720 = 1/15
To learn more about the probability;
brainly.com/question/11234923
#SPJ1
What is the remainder when 3x^3-5x^2-23x+24 is divided by x-3?

Answers
The remainder you got when 3x³ - 5x² - 23x + 24 is divided by x - 3 is -9.
What is Polynomials?Polynomials are expressions in algebra which consist of both variables and coefficients. Sometimes, variables are also known as indeterminates. Polynomials are classified as monomials, binomials, and trinomials based on the degree of the variables in the expression.
Variables in the monomials, binomials and trinomials have the highest degree equals 1, 2 and 3 respectively.
By doing the long division method, we will bet the quotient as 3x² + 4x - 11 and the remainder equals -9.
Let's check this using division algorithm.
Dividend = 3x³ - 5x² - 23x + 24
Divisor = x - 3
Quotient = 3x² + 4x - 11
Remainder = -9
By division algorithm,
Dividend = (Divisor × Quotient) + Remainder
3x³ - 5x² - 23x + 24 = [(x - 3) (3x² + 4x - 11)] + -9
= [3x³ + 4x² - 11x - 9x² - 12x + 33] + -9
= 3x³ + 4x² - 9x² - 11x - 12x + 33 - 9
= 3x³ - 5x² - 23x + 24
Hence -9 is the remainder of this division process.
To learn more about Polynomials, click on the link given below:
https://brainly.com/question/11536910
#SPJ1
Find the LCM of A= 3^2 x 5^4 x 7 and B= 3^4 x 5^3 x 7 x11
Answers
The LCM of A = 3² × 5⁴ × 7 and B = 3⁴ × 5³ × 7 × 11 is 3898125 using Prime factorization.
Given are two numbers which are showed in the prime factorized form.
A = 3² × 5⁴ × 7
B = 3⁴ × 5³ × 7 × 11
Prime factorization is the factorization of a number in terms of prime numbers.
In order to find the LCM of these two numbers, we have to first match the common primes and write down vertically when possible and then bring down the primes in each column.
A = 3² × 5³ × 5 × 7
B = 3² × 3² × 5³ × 7 × 11
Bring down the primes in each column.
LCM = 3² × 3² × 5³ × 5 × 7 × 11
= 3898125
Hence the LCM is 3898125.
Learn more about LCM here :
https://brainly.com/question/6756370
#SPJ1
Determin whether the relation defines a function, and give the domain and range.

Answers
The relation is not a function if its domain is on the x-axis and its range is on the y-axis. However, if the relation's domain is on the y-axis and its range is on the x-axis, it is a function.
If so, what kind of function is it?
Relationships are defined by three factors:
1. domain is a set of inputs.
2. an output set referred to as range.
3 . relationships between domain and range-related items.
If and only if each element of the domain is associated to just one member of the range, is a relation a function. It must be noted that the solution may vary based on the domain and range that we assume.
The provided relation is a function if the x-axis is the range and the y-axis is the domain, as opposed to when the x-axis is the domain and the y-axis is the range.
To learn more about this visit , https://brainly.com/question/28574205
#SPJ9