Kim is creating a mosaic in her garden. She finds the tile below and wants to know the missing side length ‘x’. Calculate the missing side length to a reasonable level of accuracy, explain your decision.

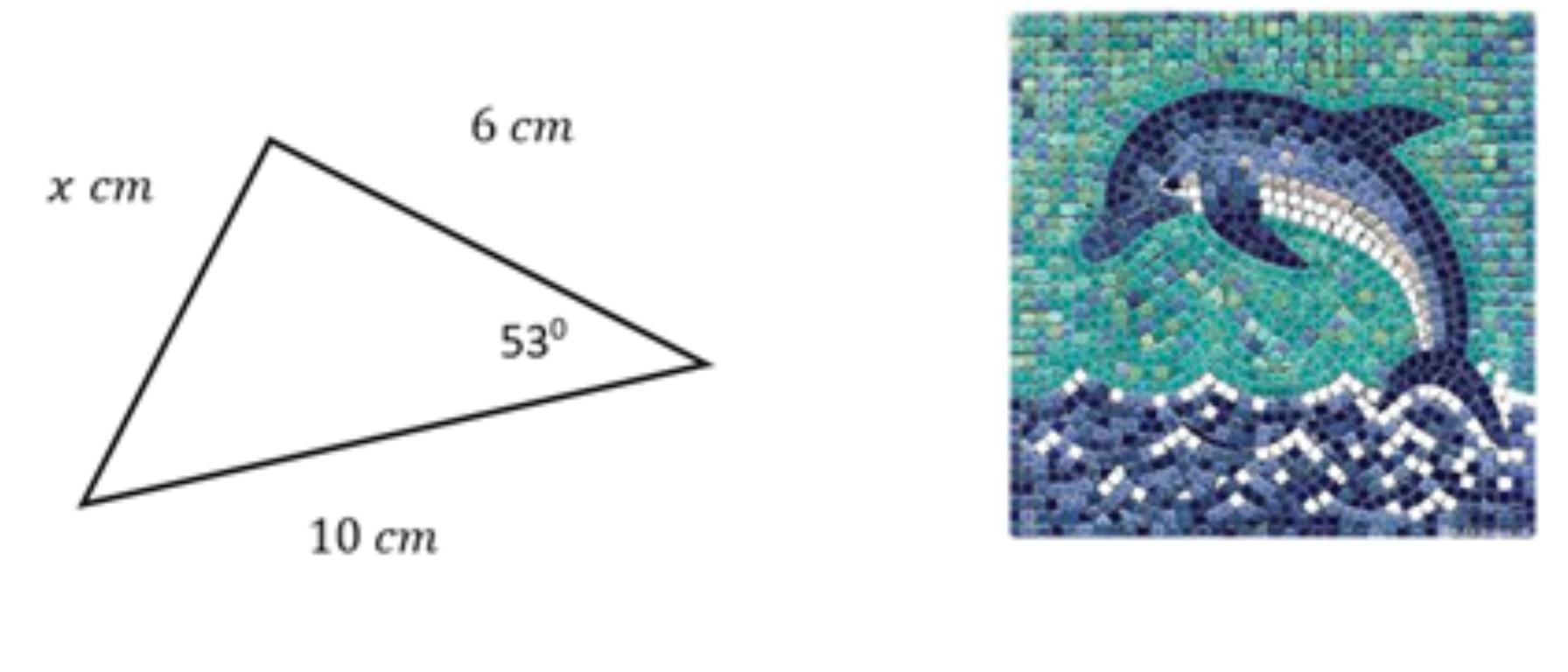
Answer:

X=100 is the answer ,,,,

Answer:

i used the (b•h)/2 formula  <--------------1

Step-by-step explanation                    1

that is the answer above this -----------1

Answer: (100,000, 10,000,000]

Step-by-step explanation:

The interval is given by ( 100,000 , 10,000,000], the correct option is C.

The threshold value is the minimum value above which the desired results can be expected.

The decibel reading was consistently above 50, but never above 70.

d = 10log(x)

50 = 10log(x)

5 = log x

10⁵ = x

x > 10⁵

d = 10log(x)

70 = 10log(x)

x = 10⁷

From the given data

x ≤ 10⁷

Therefore, the interval is given by ( 100,000 , 10,000,000], the correct option is C.

To know more about Threshold value

https://brainly.com/question/13031415

#SPJ2

The inherent zero is simply a zero. The three instances for both are-

The absolute zero is another name for the intrinsic zero. This is not included in the interval scale because, while the disparity between the two observations makes sense, the ratio does not because it lacks an inherent zero.

Some key features of inherent zero are-

To know more about the inherent zero, here

https://brainly.com/question/18558553

#SPJ4

There are 18816 ways to place five indistinguishable rooks on an 8x8 chessboard such that no rook can attack another, and neither the first row nor the first column is empty.

Since the first row and the first column cannot be empty, we need to choose one cell in each of these rows and columns to place the rooks.

Let's break down the problem into steps:

Choose a cell in the first row to place the first rook: There are 8 options.

Choose a cell in the first column to place the second rook: There are 8 options.

Choose a cell in the remaining 7 rows to place the third rook: There are 7 options.

Choose a cell in the remaining 7 columns to place the fourth rook: There are 7 options.

Choose a cell in the remaining 6 rows to place the fifth rook: There are 6 options.

To find the total number of ways, we multiply the number of options for each step:

Total number of ways = 8 × 8 × 7 × 7 × 6 = 18816.

Therefore, there are 18816 ways to place five indistinguishable rooks on an 8x8 chessboard such that no rook can attack another, and neither the first row nor the first column is empty.

Learn more about the permutations here:

https://brainly.com/question/1216161

#SPJ4

Answer:

20. AB = 42

21. BC = 28

22. AC = 70

23. BC = 20.4

24. FH = 48

25. DE = 10, EF = 10, DF = 20

Step-by-step explanation:

✍️Given:

AB = 2x + 7

BC = 28

AC = 4x,

20. Assuming B is between A and C, thus:

AB + BC = AC (Segment Addition Postulate)

2x + 7 + 28 = 4x (substitution)

Collect like terms

2x + 35 = 4x

35 = 4x - 2x

35 = 2x

Divide both side by 2

17.5 = x

AB = 2x + 7

Plug in the value of x

AB = 2(17.5) + 7 = 42

21. BC = 28 (given)

22. AC = 4x

Plug in the value of x

AC = 4(17.5) = 70

✍️Given:

AC = 35 and AB = 14.6.

Assuming B is between A and C, thus:

23. AB + BC = AC (Segment Addition Postulate)

14.6 + BC = 35 (Substitution)

Subtract 14.6 from each side

BC = 35 - 14.6

BC = 20.4

24. FH = 7x + 6

FG = 4x

GH = 24

FG + GH = FH (Segment Addition Postulate)

\( 4x + 24 = 7x + 6 \) (substitution)

Collect like terms

\( 4x - 7x = -24 + 6 \)

\( -3x = - 18 \)

Divide both sides by -3

\( x = 6 \)

FH = 7x + 6

Plug in the value of x

FH = 7(6) + 6 = 48

25. DE = 5x, EF = 3x + 4

Given that E bisects DF, therefore,

DE = EF

5x = 3x + 4 (substitution)

Subtract 3x from each side

5x - 3x = 4

2x = 4

Divide both sides by 2

x = 2

DE = 5x

Plug in the value of x

DE = 5(2) = 10

EF = 3x + 4

Plug in the value of x

EF = 3(2) + 4 = 10

DF = DE + EF

DE = 10 + 10 (substitution)

DE = 20

We square the residuals when using the least-squares line method to find the line of best fit because we believe that huge negative residuals (i.e., points well below the line) are just as harmful as large positive residuals (i.e., points that are high above the line).

We treat both positive and negative disparities equally by squaring the residual values.  We cannot discover a single straight line that concurrently minimizes all residuals. The average (squared) residual value is instead minimized.

We might also take the absolute values of the residuals rather than squaring them. Positive disparities are viewed as just as harmful as negative ones under both strategies.

To know more about the Least-Squares Line method, visit:

https://brainly.com/question/14940432

#SPJ4

A: \(3x^2y^4\cdot2x^6y=6x^8y^5\)

B: \(xz^3\cdot4x^4z^5=4x^5z^8\)

C: \(4a^3^2\cdot 3a^6b^5=12a^{15}b^5\)

D: \(6s^{5t}\cdot s^{4t}^2=6s^{16t^2+5t}\)

There was some ambiguity you posed with such exponents but I assumed strictly.

Hope this helps.

Based on the mean miles between the services and the standard deviation, the probability that the mean of 32 cars as a sample would be less than 4,424 miles is 0.0027.

The required probability is for the possibility that in a sample of 32 cars, the number of services would be less than 4,424.

The probability can be found by the formula:

P (x < 4,424) = P ( Z < (4,424 - 4,639) / (437 / √32))

This gives us:
P (x < 4,424) = P ( Z < -2.78)

Using the Z table shows that the probability would be 0.0027.

Find out more on probability at https://brainly.com/question/26045714

#SPJ1

Answer:

centre = (0, 0 ) , radius = 2

Step-by-step explanation:

the equation of a circle centred at the origin is

x² + y² = r² ( r is the radius )

x² + y² = 4 ← is in this form

with centre (0, 0 ) and r = \(\sqrt{4}\) = 2

Explanation:

A relation is a function if and only if for each value of x there's only one value of y. In other words, if we find one value of x more than once, the relation is not a function.

Relation A is not a function because x = 2 shows up twice: (2, 5) and (2, 7)

Relation C is not a function because x = 1 shows up three times: (1, 3), (1, 5) and (1, 7)

Relation E is not a function because x = 2 shows up twice: (2, 5) and (2, 1)

Relations B and D have only one time each value of x

Answers:

The equivalent units for the Compounding Department for August 2019 is 57,000 pounds.

Here is the explanation -

To calculate the equivalent units for the Compounding Department in August 2019 using the weighted average method, we need to consider the units that were started and completed, as well as the ending work-in-process.

Step 1: Calculate the equivalent units for units started and completed:
- 36,000 pounds were started.
- 34,000 pounds were transferred out.
Equivalent units for units started and completed = 34,000 pounds.

Step 2: Calculate the equivalent units for ending work-in-process:
- Ending work-in-process was 70% processed.
- Beginning work-in-process was 2,000 pounds (60% processed).
Equivalent units for ending work-in-process = (70% x Ending work-in-process) + (60% x Beginning work-in-process)
Equivalent units for ending work-in-process = (70% x 2,000 pounds) + (60% x 36,000 pounds)
Equivalent units for ending work-in-process = 1,400 pounds + 21,600 pounds
Equivalent units for ending work-in-process = 23,000 pounds.

Step 3: Calculate the total equivalent units:
Total equivalent units = Equivalent units for units started and completed + Equivalent units for ending work-in-process
Total equivalent units = 34,000 pounds + 23,000 pounds
Total equivalent units = 57,000 pounds.

Therefore, the equivalent units for the Compounding Department for August 2019 is 57,000 pounds.

To know more on Weighted average visit:

https://brainly.com/question/28334973

#SPJ11

Answer:

Circumference is the length around a circle (2Pr) while area is a measure of square units inside the circle (Pr2).

Step-by-step explanation:

hope it helps!

Let me give you an example.

Consider you have a circular field.

Circumference: Putting a fence around the field. This is measuring distance.

Area: Ploughing the field entirely. How much space INSIDE THE CIRCLE do you need to plow? That is the area.

To solve this problem :
A = P(1 + r/n)^(nt)
Where:
A = the final amount
P = the principal amount (the initial investment)
r = the annual interest rate (as a decimal)
n = the number of times the interest is compounded per year
t = the number of years
In this case, we have:
P = $46,950.00
r = 6.78% = 0.0678
n = 2 (since the interest is compounded semi-annually)
t = 12 (since we are investing for 12 years and withdrawing at the end of every three months)

To find the amount that can be withdrawn, we need to solve for A when t = 12/4 = 3 (since we are withdrawing every three months):
A = P(1 + r/n)^(nt)
A = $46,950.00(1 + 0.0678/2)^(2*3)
A = $46,950.00(1.0339)^6
A = $46,950.00(1.2307)
A = $57,789.27
So the sum of money that can be withdrawn from the fund is $57,789.27.

To learn more about Simple & Compound Interest : https://brainly.com/question/16752173

#SPJ11

Mrs. Staviski will get 4 sections if she cuts a 2-foot long piece of yarn into 1/2-foot sections.

If Mrs. Staviski divides a 2-foot-long strand of yarn into 1/2-foot-long sections

We must divide the overall length of the yarn by the length of each segment to see how many sections will result:

2 feet long divided by 1/2 foot per segment equals (2*2) / 1 = 4 sections

Therefore, Mrs. Staviski will get 4 sections if she cuts a 2-foot long piece of yarn into 1/2-foot sections.

Learn more about  sections at https://brainly.com/question/3603397

#SPJ1

Answer:

x = 10

Step-by-step explanation:

7(x - 6) = 28

Expand the equation:

7x - (7 x 6) = 28

7x - 42 = 28

Move x-term to one side, numbers to the other side:

7x = 28 + 42

7x = 70

x = 70/7

x = 10

The value of x will be; x = 10

An equation is an expression that shows the relationship between two or more numbers and variables.

We are given that the equation

7(x - 6) = 28

Expand the equation:

7x - (7 x 6) = 28

7x - 42 = 28

Now Move x-term to one side, numbers to the other side:

7x = 28 + 42

7x = 70

x = 70/7

x = 10

The value of x will be; x = 10

Learn more about equations here;

brainly.com/question/25180086

#SPJ2

The equation log3(2x - 2) = 3 can be rewritten without logarithms by using the exponentiation property of logarithms.

In exponential form, the equation becomes 3^3 = 2x - 2.

Simplifying further, we have 27 = 2x - 2.

To solve this equation, one would isolate the variable x by adding 2 to both sides of the equation, resulting in 29 = 2x. Finally, dividing both sides by 2 gives the solution x = 29/2.

Therefore, the equation log3(2x - 2) = 3 is equivalent to the equation 27 = 2x - 2, and the solution in exact form is x = 29/2.

learn more about Properties of logarithms here: brainly.com/question/12049968

#SPJ11

The natural log of 5 equals about 1.6 and the natural log of 5000 equals about 8.5.

To calculate these values, you can use the logarithmic function. The natural logarithm, denoted as ln, is the logarithm to the base e (approximately 2.71828). To find the natural log of a number, you can use a scientific calculator or mathematical software.
For the first part of the question, ln(5) is approximately 1.6094. Rounded to the nearest tenth, it is about 1.6. For the second part of the question, ln(5000) is approximately 8.5172. Rounded to the nearest tenth, it is about 8.5. Therefore, the correct answer is: about 1.6; about 8.5.

To know more about the natural log, visit:

https://brainly.com/question/30287528

#SPJ11

Answer: Approximately 31 number keys.

Step-by-step explanation: Ratio is a comparison between two values.

Ratio for number keys to letter keys is \(\frac{3}{15}\), which means each 3 group of number keys is equivalent to 15 letter keys.

The producer will need

\(\frac{3}{15} =\frac{x}{156}\)

\(x=\frac{3.156}{15}\)

x = 31

The manufacturer will need to be produced 31 keys.

Amplitude of f  -\(x^{2}\)+100x - 1200 is 350.

To find the amplitude of a periodic function, we need to find the maximum and minimum values of the function over one period and then take half of their difference.

In this case, the function f(x) is given by:

f(x) = -\(x^{2}\) + 100x - 1200, 0 ≤ x ≤ 100

To find the maximum and minimum values of f(x) over one period, we can use calculus by taking the derivative of f(x) and setting it equal to zero:

f'(x) = -2x + 100

-2x + 100 = 0

x = 50

So the maximum and minimum values of f(x) occur at x = 0, 50, and 100. We can evaluate f(x) at these values to find the maximum and minimum values:

f(0) = -\(0^{2}\) + 100(0) - 1200 = -1200

f(50) = -\(50^{2}\) + 100(50) - 1200 = -500

f(100) = -\(100^{2}\) + 100(100) - 1200 = -1200

Therefore, the maximum value of f(x) over one period is -500 and the minimum value is -1200. The amplitude is half of the difference between these values:

Amplitude = (Max - Min)/2 = (-500 - (-1200))/2 = 350

Therefore, the amplitude of f(x) is 350.

Correct Question :

suppose that f is a periodic function with period 100 where f(x) = -\(x^{2}\)+100x - 1200 whenever 0 ≤x≤100. what is amplitude of f.

To learn more about Amplitude here:

https://brainly.com/question/32041579

#SPJ4

Answer:

The area of the bigger lid is approximately 29.2 square inches

Step-by-step explanation:

The given data are;

The volume held by one of the cans of paint, V₁ = 64 oz

The volume held by the other cans of paint, V₂ = 125 oz

The area of the smaller lid = 18 in²

Therefore,

The 64 Oz = The smaller can of paint

The 125 oz = The larger can of paint

The diameter of the smaller lid, d₁ = √(18 × 4/π) ≈ 4.787

The ratio of can volumes = (The ratio of can diameters)³

V₁/V₂ = (d₁/d₂)³

V₁/V₂ = 64/125

d₁/d₂ ≈ 4.787/d₂

64/125 = (4.787/d₂)³

4.787/d₂ = ∛(64/125) = 4/5

d₂ ≈ 4.878×5/4 = 6.0975

The area of the bigger lid, A₂ = π·d₂²/4

∴ A₂ = π × 6.0975²/4 ≈ 29.2

The area of the bigger lid, A₂ ≈ 29.2 in.²

Answer:

x=1/4

Step-by-step explanation:

x12=3 (I would treat it as 12x=3 since the 12 is still attached with multiplication)

x=3/12 (simplify your fraction)

x=1/4

π/16 is the area enclosed by the curve r= sin(4θ)

The given curve is polar curve and hence the area of the polar curve is given by:

Let A be the area of the curve so,

A = \(\int\limits^b_a {\frac{1}{2}r^2 } \, d\theta\)

where a and b is the boundary at which r=0

so after equation r=0

sin(4θ) =0

=> sin(4θ) =0

=> 4θ = 0,π

=> θ = 0, π/4

so a=0 , b= π/4

now  

  A =  \(\int\limits^b_a {\frac{1}{2}r^2 } \, d\theta\)   ------(i)

so   \(r^2\) = (sin(4θ))^2

=>   \(sin^2\)( 4θ )

ans we know that

cos(2α) = 1 -  \(2sin^2\)2 α

so     \(sin^2\)= (1- cos(8θ) )/2

putting the value of r in the equation (i) we get :-

A = \(\int\limits^b_a {\frac{1}{4} *(1-cos8\theta) } \, d\theta\)

=> 1/4*  \(\int\limits^b_a {(1-cos8\theta) } \, d\theta\)

here a=0 and b=π/4

after putting the value and solving the integral

A = π/16

so A is the area enclosed by r=sin(4θ) is π/16

To know more about polar curve click on below link:

brainly.com/question/1094340#

#SPJ4

Answer:

y=3x+1.4 (???)

Step-by-step explanation:

You didn't provide a slope or any points on the graph so I'm assuming you can just make whatever number you fancy the slope. Not very sure what you mean by this question... Try to give more info of the question!

Answer:

Use colon method

Step-by-step explanation:

So it is more easy

Answer:

38^3+10^2+26x+3 over 18x+1

Step-by-step explanation:

Start by adding x's that are alike together.

4x^3+34x^3= 38^3

then do the same to the other x's

5x^2+5x^2= 10^2

Last x's

13x+13x=26x

For the final equation, you should have

38^3+10^2+26x+3

For the bottom equation, you do the same thing.

4x+14x= 18x

Final equation, really easy, is 18x+1

For the final answer you should have

38^3+10^2+26x+3 over 18x+1

Lmk if it helps!! :)

As per the information provided, a = 4√3/3 + 4, b = 4 - 4√3/3 the answer can be calculated with optimization method. it will be as follows:

Sum of a and b is 8, we get

a+b=8

b=8−a

Now, let x=a−b

Then we get,

\(x=a−(8−a) \\ x=2a−8 \\ x+8=2 \\ 1 \div 2x+4=a

\)

we use this to answer to solve for b

\(b=8−a \\ =8−(1 \div 2x+4) \\ =4−1 \div 2x

\)

Now we use the product of two numbers and its difference. This can be expressed as:

\(a⋅b⋅x=(1 \div 2x+4)(4−1 \div 2x) \\ x=2 {x}^{2} − \frac{1}{4} {x}^{3} +16x−2x^{2} \\ =−14x^{3} +16x

\)

Thus, this expression that we need to maximize. Take the derivative, set it equal to zero, and solve for x

\(−3 \div 4x ^{2} +16=0 \\ 16 =3 \div 4 x ^{2} \\ 643=x \\ 28√3 \div 3=x\)

Now for us to check that this is a maximum, we have to note that the second derivative is

\(−3 \div 2x

\\ At \\

x=8√3 \div 3

\)

the second derivative is −4√3. Since this number is negative, the point is a maximum.

Now we must find the values of a and b for this x. We have to use the relationship

\(a=1 \div 2x+4\)

\(a=1 \div 2 \times 8√3 \div 3+4 \\ =4√3 \div 3+4\)

now we use the relationship b=8−a

\(b=8−(4√3 \div 3+4) \\ =4−4√3 \div 3\)

The first step in determining a function's maximum or minimum value is differentiating it. Then, set this derivative to zero and conduct the computation.

x. This will reveal the location of a function's maximum or minimum, but it won't reveal which.

Take the second derivative to get more details. A local maximum occurs when both the first and second derivatives are negative. You have a local minimum when both the first derivative and the second derivative are zero.

To learn more about optimization: https://brainly.com/question/28970005

#SPJ4

The point that preserves the function is option  A(-3,-8).

What do you mean by function?

A function in mathematics from a set X to a set Y assigns exactly one element of Y to each element of X. The sets X and Y are collectively referred to as the function's domain and codomain, respectively.

According to the given question,

We have four option for the answer.

Note: if f is a function then each number of the domain has an unique image.

Since (regarding the table) the image of 9 is 6 then the answer D is wrong

The same apply on answers B and C .

Therefore, the right answer is A(-3,-8).

To learn more about function, visit:

brainly.com/question/5975436?referrer=searchResults

#SPJ1