Kenji and Ramon are running cro country. Kenji run at a rate of 150 meter per minute
Answers
Kenji and Ramon are at a distance of 750 m after a time interval of 1 hour from each other.
Kenji runs for a total time of 60 minutes + 15 minutes = 75 minutes.
Ramon runs for a total of 60 minutes.
Now, we find the total distance covered by Kenji and Ramon in the time intervals of 75 minutes and 60 minutes respectively.
Kenji runs a total distance of 150 meters/minute * 75 minutes = 11250 meters.
Ramon runs a total distance of 200 meters/minute * 60 minutes = 12000 meters.
Now, we find the difference in their distances.
The distance between Kenji and Ramon is 12000 meters - 11250 meters = 750 meters.
Learn more about Distance at:
brainly.com/question/26046491
#SPJ4
Complete Question:
Kenji and Ramon are running cross country. Kenji run at a rate of 150 meter per minute and Ramon runs at a rate of 200 meters per minute. If Kenji starts 15 minutes before Ramon, how far apart are they after one hour?
Related Questions
Find the value of x.
5
X
11
y

Answers
The value of the variable is 4√5. Then the correct option is C.
What is the triangle?A triangle is a three-sided polygon with three angles. The angles of the triangle add up to 180 degrees.
The similar triangles are shown in the diagram.
16 / x = x / 5
x² = 16 × 5
x = 4 √5
Then the value of the variable is 4√5.
Then the correct option is C.
More about the triangle link is given below.
https://brainly.com/question/25813512
#SPJ1

. find a set of smallest possible size that has both {1, 2, 3, 4, 5} and {2, 4, 6, 8, 10} as subsets
Answers
Hi! To find a set of the smallest possible size that has both {1, 2, 3, 4, 5} and {2, 4, 6, 8, 10} as subsets, follow these steps:
1. List out the given subsets: {1, 2, 3, 4, 5} and {2, 4, 6, 8, 10}.
2. Combine the elements of both subsets without repeating any numbers: {1, 2, 3, 4, 5, 6, 8, 10}.
3. The combined set is {1, 2, 3, 4, 5, 6, 8, 10}, which has a size of 8.
So, the smallest possible set that has both {1, 2, 3, 4, 5} and {2, 4, 6, 8, 10} as subsets is {1, 2, 3, 4, 5, 6, 8, 10}.
The smallest possible set that includes both {1, 2, 3, 4, 5} and {2, 4, 6, 8, 10} subsets is {1, 2, 3, 4, 5, 6, 8, 10}.
To find a set of the smallest possible size that has both {1, 2, 3, 4, 5} and {2, 4, 6, 8, 10} as subsets, follow these steps:
1. Identify the given subsets: {1, 2, 3, 4, 5} and {2, 4, 6, 8, 10}.
2. Combine the elements from both subsets without repeating any numbers.
3. Organize the combined elements in ascending order.
Your answer: The smallest possible set that includes both subsets is {1, 2, 3, 4, 5, 6, 8, 10}.
To learn more about subsets, refer:-
https://brainly.com/question/24138395
#SPJ11
Hi! To find a set of the smallest possible size that has both {1, 2, 3, 4, 5} and {2, 4, 6, 8, 10} as subsets, follow these steps:
1. List out the given subsets: {1, 2, 3, 4, 5} and {2, 4, 6, 8, 10}.
2. Combine the elements of both subsets without repeating any numbers: {1, 2, 3, 4, 5, 6, 8, 10}.
3. The combined set is {1, 2, 3, 4, 5, 6, 8, 10}, which has a size of 8.
So, the smallest possible set that has both {1, 2, 3, 4, 5} and {2, 4, 6, 8, 10} as subsets is {1, 2, 3, 4, 5, 6, 8, 10}.
The smallest possible set that includes both {1, 2, 3, 4, 5} and {2, 4, 6, 8, 10} subsets is {1, 2, 3, 4, 5, 6, 8, 10}.
To find a set of the smallest possible size that has both {1, 2, 3, 4, 5} and {2, 4, 6, 8, 10} as subsets, follow these steps:
1. Identify the given subsets: {1, 2, 3, 4, 5} and {2, 4, 6, 8, 10}.
2. Combine the elements from both subsets without repeating any numbers.
3. Organize the combined elements in ascending order.
Your answer: The smallest possible set that includes both subsets is {1, 2, 3, 4, 5, 6, 8, 10}.
To learn more about subsets, refer:-
https://brainly.com/question/24138395
#SPJ11
g a pharmaceutical company receives large shipments of ibuprofen tablets and uses an acceptance sampling plan. this plan randomly selects and tests 29 tablets, then accepts the whole batch if there is at most one that doesn't meet the required specifications. what is the probability that this whole shipment will be accepted if a particular shipment of thousands of ibuprofen tablets actually has a 4% rate of defects? (report answer as a decimal value accurate to four decimal places.)
Answers
The probability that this whole shipment will be accepted if a particular shipment of thousands of ibuprofen tablets actually has a 4% rate of defects is 0.9660
This problem can be solved by permutations and combinations. This can also be solved using binomial probability experiment.
Let, then we could reasonably assume that follows a binomial distribution.
Given P = 0.01 and n = 29
P(x) = nCx.px.(1-p)^(n-x)
nCx = n! [x!-(n-x)!]
P = P(X<=1).
X<=1, if X = 0 and X = 1,
P(0) + P(1)
P(0) = 1.(0.01)^(0).(0.99)^(29) = 0.74717
P(1) = 29C1.(0.01)^(1).(1-0.01)^(29-1)
P(1) = 0.21887
P = P(0) + P(1)
P = 0.74717+0.21887 = 0.9660
So, therefore the probability that this whole shipment will be accepted if a particular shipment of thousands of ibuprofen tablets actually has a 4% rate of defects is 0.9660
Learn more about probability here:
https://brainly.com/question/30034780
#SPJ4
In WXY, m/W = (10x + 17)°, m/X = (2x - 9)°, and m/Y = (3x + 7)°. Find m/Y.

Answers
Answer:
m∠Y = 40°
Step-by-step explanation:
The sum of the three angles of a triangle must equal 180°
Thus
m∠W + m∠X + m∠y = 180°
→ (10x + 17) + (2x - 9) + (3x + 7) = 180
→ 10X + 17 + 2X + 9 + 3X + 7 = 180
Collecting like terms
→ 10X + 2X + 3X + 17 - 9 + 7 = 180°
→ 15x + 15 = 180
Subtract constant 15 from both ssides:
→ 15x + 15 - 15 = 180 - 15
→ 15x = 165
Divide both sides by 15
→ 15x/15 = 165/15
→ x = 11
m∠Y = 3x + 7
m∠Y = 3 x 11 + 7
m∠Y = 33 + 7
m∠Y = 40°
What is the value of x? Round to the nearest tenth(1 decimal place)

Answers
Answer:jkkjjkj098765
Step-by-step explanation:
iuytrfdghyui8
angelina drove at an average rate of 80 kph and then stopped 20 minutes for gas. after the stop, she drove at an average rate of 100 kph. altogether she drove 250 km in a total trip time of 3 hours including the stop. which equation could be used to solve for the time $t$ in hours that she drove before her stop?
Answers
Angelina drove for 0.83 hours (or approximately 50 minutes) before her stop.
The equation that could be used to solve for the time $t$ in hours that Angelina drove before her stop is:
$80t + 100(3 - t - \frac{1}{3}) = 250$
Let's break down the information given. Angelina drove at an average rate of 80 kph for a certain amount of time, which we want to find. After that, she stopped for 20 minutes (or $\frac{1}{3}$ of an hour) for gas. Then, she continued driving at an average rate of 100 kph. The total trip time, including the stop, was 3 hours.
To solve for the time Angelina drove before her stop, we can set up an equation based on the distance she traveled. The distance traveled at 80 kph is given by $80t$, where $t$ represents the time in hours. The distance traveled after the stop at 100 kph is $100(3 - t - \frac{1}{3})$, where $3 - t - \frac{1}{3}$ represents the remaining time after the stop.
The sum of these distances should equal the total distance traveled, which is 250 km. Therefore, we set up the equation $80t + 100(3 - t - \frac{1}{3}) = 250$.
By solving this equation, we can find the value of $t$, which represents the time in hours that Angelina drove before her stop.
To solve the equation, we can start by simplifying the expression on the right side:
$80t + 100(3 - t - \frac{1}{3}) = 250$
First, we can simplify the expression $3 - t - \frac{1}{3}$:
$3 - t - \frac{1}{3} = 2\frac{2}{3} - t = \frac{8}{3} - t$
Now, we substitute this expression back into the equation:
$80t + 100(\frac{8}{3} - t) = 250$
Next, we distribute the 100 to both terms inside the parentheses:
$80t + \frac{800}{3} - 100t = 250$
Combining like terms:
$-20t + \frac{800}{3} = 250$
To isolate the variable $t$, we can subtract $\frac{800}{3}$ from both sides:
$-20t = 250 - \frac{800}{3}$
To simplify the right side, we need a common denominator for 250 and $\frac{800}{3}$, which is 3:
$-20t = \frac{750}{3} - \frac{800}{3}$
Subtracting the fractions:
$-20t = \frac{-50}{3}$
Finally, we divide both sides by -20 to solve for $t$:
$t = \frac{\frac{-50}{3}}{-20} = \frac{50}{60} = \frac{5}{6}$
Therefore, Angelina drove for $\frac{5}{6}$ or 0.83 hours (or approximately 50 minutes) before her stop.
Learn more about approximately here:
brainly.com/question/31695967
#SPJ11
A bag contains 10 marbles. Four of them are red, three blue, two white, and one yellow. A marble is drawn at random. What is the probability that it is yellow?
Answers
Answer: It is one out of ten or 1/10 or 10%
what is the ration that equivalent to 6/7
Answers
An equivalent ratio of the given ratio 6/7 is; 12/14
How to find Equivalent Ratios?To find equivalent ratios, we will just multiply the given ratio by any number that is equivalent to 1 such as 2/2, 3/3, 4/4, 5/5 e.t.c
Now, we want to find equivalent ratio of 6/7. Applying the procedure above, we can say that;
Equivalent ratio = (6/7) * (2/2) = 12/14
Thus, an equivalent ratio of 6/7 is; 12/14
Read more about Equivalent Ratios at; https://brainly.com/question/2328454
#SPJ1
The cost, in dollars, for a video game developer to code g games can be represented by the function v(g) . The number of games produced in w weeks is given by the function g(w) = 4w.
Answers
After w weeks, the expression for the total cost of games is 250 + 4000w.
What is Expression?
Mathematical expressions consist of at least two numbers or variables, at least one arithmetic operation, and a statement. It's possible to multiply, divide, add, or subtract with this mathematical operation. An expression's structure is as follows: Expression: (Math Operator, Number/Variable, Math Operator)
An algebraic expression known as a linear expression has terms that are either constants or variables raised to the first power. Alternatively put, none of the exponents can be greater than 1.
As an illustration, while x is a variable raised to the first power, x2 is a variable raised to the second power. An illustration of a constant is 5.
Linear expressions are what the two expressions are. One variable raised to the power of one makes up a linear expression.
250 + 1000g.
Where: g(w) = 4w.
250 + 1000(4w).
250 + 4000w.
Therefore, number of games produced in w weeks is 250 + 4000w.
Learn more about mathematical expression click here;
https://brainly.com/question/4344214
#SPJ4
please help with these 3 questions

Answers
Answer:
1. D) Both b) and c)
2. B) Cosine Law
3. B) Find the measures of angles and sides that we can't physically measure.
Step-by-step explanation:
1. To solve non-right triangles we use Sine Law and Cosine Law.
2. If 3 sides lengths were given and you were asked to find an angle, you would use the Cosine Law.
3.Trigonometry is used in real life to find the measures of angles and sides that we can't physically measure.
You shoot a basketball to try to knock your friend’s shot away from the hoop. The height (in feet) of your friend's basketball t seconds after he shoots is represented by -16t^2+25t+6.25. The height (in feet) of your basketball t seconds after you shoot is represented by -16t^2+20t+5.5. You and your friend shoot at the same time. Is it possible for the basketballs to collide? Explain.

Answers
Answer: No
Step-by-step explanation:
No, it is not possible for the basketballs to collide.
What is a quadratic equation?For variable x : ax² + bx + c = 0, where a≠0 is a standard quadratic equation, which is a second-order polynomial equation in a single variable. It has at least one solution since it is a second-order polynomial equation, which is guaranteed by the algebraic basic theorem.
Given:
You shoot a basketball to try to knock your friend’s shot away from the hoop.
The height (in feet) of your friend's basketball t seconds after he shoots is represented by -16t² + 25t + 6.25.
The height (in feet) of your basketball t seconds after you shoot is represented by -16t² + 25t + 5.5.
You and your friend shoot at the same time.
That means,
-16t² + 25t + 6.25 = -16t² + 25t + 5.5.
6.25 ≠ 5.5
Hence, no collision is possible.
To learn more about the quadratic equation;
https://brainly.com/question/17177510
#SPJ1
How do you graph parent functions and transformations?
Answers
The rules to plot the graph of the transformed function is explained clearly.
How to transform a graph of the function?The graph of a function can be transformed by either shifting it in the right, left, up or down.
When the transformation is rightwards, the function becomes as g(x - a).
For left shifting it is g(x + a).
Suppose the function be g(x).
The transformation of g(x) implies change of its position on the coordinate axis as well as its size keeping the shape as the same.
If it is shifted by h units rightwards.
Then, it can be written as g(x - h)
For left shift of h units it is given as g(x + h).
Both the above transformation implies that the function f(x) will have same value at x = 0 and x = h or x = -h.
Similarly, it can be dilated as ag(x).
Which signifies the value of g(x) at any value of x is increased by a factor of a.
Hence, the graph of a transformed function can be plotted by using the rules explained in the answer.
To know more about transformation of graph click on,
https://brainly.com/question/10059147
#SPJ4
Functions, graphs, combining functions. Trigonometric, Exponential, Logarithmic and Inverse Functions Functions, graphs, combining functions. Trigonometric, Exponential, Logarithmic and Inverse Functions
Answers
Functions, graphs, and combining functions are essential concepts in mathematics. Trigonometric, exponential, logarithmic, and inverse functions each have unique characteristics and can be represented graphically
Functions, graphs, and combining functions are important concepts in mathematics.
Trigonometric functions, exponential functions, logarithmic functions, and inverse functions are all types of functions that can be represented graphically.
Trigonometric functions, such as sine, cosine, and tangent, are used to model periodic phenomena and have specific patterns in their graphs.
Exponential functions, on the other hand, grow or decay rapidly and are commonly used to represent population growth, radioactive decay, or compound interest. Logarithmic functions are the inverse of exponential functions and are used to solve equations involving exponential quantities.
When it comes to combining functions, you can perform operations such as addition, subtraction, multiplication, and composition. Addition and subtraction involve adding or subtracting corresponding values of two or more functions.
Multiplication combines the outputs of two functions by multiplying them together. Composition is the process of applying one function to the output of another function.
To understand functions better, it is helpful to graph them. Graphing functions allows you to visualize their behavior, identify key features such as intercepts and asymptotes, and make predictions based on the graph.
In summary, functions, graphs, and combining functions are essential concepts in mathematics. Trigonometric, exponential, logarithmic, and inverse functions each have unique characteristics and can be represented graphically.
Understanding these concepts and their graphs can help solve problems and make predictions in various fields of study.
to learn more about logarithmic
https://brainly.com/question/30226560
#SPJ11
In a rectangle , the diagonal amount with the base is 72.
The diagonal is 2 cm bigger than the base.
Find the perimeter and S of the rectangle.
Answers
The rectangle in the example has a 173.70 cm perimeter.
What is Perimeter?The perimeter of a form is the space surrounding its edge. you can find the perimeter of various forms by summing the lengths of their sides.
Given, In a rectangle, the diagonal amount with the base is 72. The diagonal is 2 cm bigger than the base.
Since the Diagonal is 72 cm
and also given base = diagonal - 2
Base = 70
Because Diagonal ² = base² + height²
height² = 72² - 70²
Height² = 284
Height = 16.85
Thus the perimeter = 2*(base + height)
Perimeter of rectangle = 2 * (70 + 16.85)
the perimeter of the rectangle = 173.70
Therefore, the perimeter of the given Rectangle is 173.70 cm.
Learn more about perimeter here:
https://brainly.com/question/6465134
#SPJ1
How to solve -6v - 5 > 13
Answers
Answer:
you use division then add then you get the answer
Step-by-step explanation:
HELP THIS IS DUE AT 12
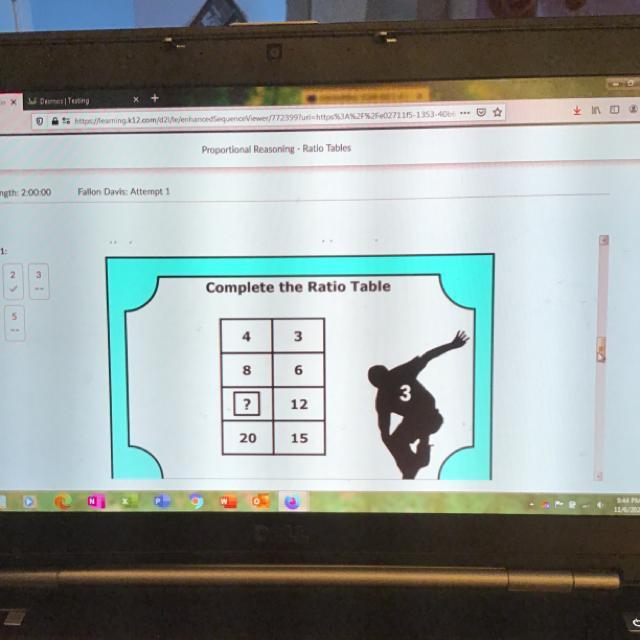
Answers
Answer:
16
Step-by-step explanation:
4×.75=3
8×.75=6
16×.75=12
20×.75=15
Answer:
whaa its the same type of question... 16...
Step-by-step explanation:
again, what grade are you in smh
If 0° SOS 90° and cose
15, what is the value of sin (90° - 9)?
A: 11/15
B: 15/11
C: 15/4
D: 4/15
Answers
The value of sin (90° - 9) is 11/15, Option A is correct.
What is Trigonometry?Trigonometry is a branch of mathematics that studies relationships between side lengths and angles of triangles.
Using the trigonometric identity sin(90° - θ) = cos(θ), we have:
sin(90° - 9) = cos(9)
To evaluate cos(9) in degrees,
cos(θ) = cos(π/2 - θ)
Substituting θ = 9 degrees, we get:
cos(9) = cos(π/2 - 9°)
Using radians, π/2 - 9° = 1.4661
cos(9) = 0.9781
Therefore, sin(90° - 9) = 0.9781, which is equivalent to 11/15 when simplified.
To learn more on trigonometry click:
https://brainly.com/question/25122835
#SPJ7
You want to buy a computer. The computer costs $1,200. How much
would you have to save every month for 6 months to be able to buy the computer? For 8 months?
Answers
Answer:
6 months: 7200
8 months: 9600
Step-by-step explanation:
Given equations:
1200 * 6
1200 * 8
Solve 6 months:
1200 * 6
= 7200
Solve 8 months:
1200 * 8
= 9600.
FILL IN THE BLANK. To find the area between two z-scores on a calculator, use the _____ To find the area between two z-scores on a calculator, use the command V command invNorm normalcdf Click to select your answer(s)
Answers
To find the area between two z-scores on a calculator, we use the command "normalcdf" on most scientific calculators.
This command calculates the area under the normal distribution curve between two specified z-scores. We need to input the two z-scores and the mean and standard deviation of the normal distribution, which can be obtained from the problem statement or by calculating them from the given data.
Another command that is used in conjunction with "normalcdf" is "invNorm". This command can be used to find the z-score corresponding to a given area under the normal distribution curve. It is used when we are given the area and we need to find the corresponding z-score.
Together, these two commands are useful for solving problems that involve normal distributions, such as finding probabilities, finding critical values, or constructing confidence intervals. It is important to understand how to use these commands properly in order to perform accurate and efficient calculations.
To know more about scientific calculators refer to-
https://brainly.com/question/29020266
#SPJ11
the life expectancy of a pug is 7.48 years. compute the residual. give your answer to two decimal places.
Answers
The residual life expectancy of a pug is approximately 2.52 years.
To compute the residual, we need to subtract the observed value (life expectancy of a pug) from the predicted value. In this case, the predicted value is 7.48 years.
Let's assume that the observed value is the average life expectancy of pugs. Please note that life expectancies can vary depending on various factors, and this figure is used here for illustration purposes.
Let's say the observed value is 10 years.
The residual can be calculated as follows:
Residual = Observed Value - Predicted Value
Residual = 10 years - 7.48 years
Residual ≈ 2.52 years
Therefore, the residual is approximately 2.52 years.
To learn more about residual
https://brainly.com/question/30243733
#SPJ11
at how many points on the curve x^2/5 y^2/5 = 1 in the xy-plane does the curve have a tangent line that is horizontal
Answers
To determine the number of points on the curve x^2/5 + y^2/5 = 1 in the xy-plane where the curve has a horizontal tangent line, we can analyze the equation and its derivative.
First, let's differentiate the equation implicitly with respect to x:
d/dx(x^2/5) + d/dx(y^2/5) = d/dx(1)
(2x/5) + (2y/5) * dy/dx = 0
Next, we solve for dy/dx:
(2y/5) * dy/dx = -(2x/5)
dy/dx = -(2x/5) / (2y/5)
dy/dx = -x / y
For a tangent line to be horizontal, the slope dy/dx must equal zero. In this case, we have:
-x / y = 0
Since the numerator is zero, we can conclude that x = 0 for a horizontal tangent line.
Substituting x = 0 back into the original equation x^2/5 + y^2/5 = 1:
0 + y^2/5 = 1
y^2/5 = 1
y^2 = 5
Taking the square root of both sides:
y = ±√5
Hence, there are two points on the curve x^2/5 + y^2/5 = 1 where the tangent line is horizontal, corresponding to the coordinates (0, √5) and (0, -√5) in the xy-plane.
Learn more about tangent here:
https://brainly.com/question/10053881
#SPJ11
Melissa had $20 to purchase candy for a party. She purchased 3.6 pounds of candy that cost $2.50 per pound. How much money does Melissa have remaining after this purchase?
Answers
Answer:
1738
Step-by-step explanation:
Melissa has $11 remaining after purchasing 3.6 pounds of candy that cost $2.50 per pound.
What is Equation?Two or more expressions with an Equal sign is called as Equation.
Melissa had $20 to purchase candy for a party.
She purchased 3.6 pounds of candy that cost $2.50 per pound
Melissa spent 3.6 x $2.50
= 9 on candy.
Subtracting this amount from her initial $20, we get:
$20 - $9 = $11
Therefore, Melissa has $11 remaining after purchasing 3.6 pounds of candy that cost $2.50 per pound.
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ2
Whos ready for finals!!!!!!!
Answers
Not really ready. But will be! FYI that's not really a question.
how much 500 grams to pounds?
Answers
500 grams is approximately equal to 1.1023 pounds ( rounded to four decimal places )
The conversion factor to convert grams to pounds is 0.00220462
1 gram = 0.00220462 pounds
The conversion is the process of changing the unit of one quantity to another units
The conversion factor is defined as the number that is used to change one unit to another units by multiplying or dividing
The mass in pounds = The mass in grams × conversion factor
Substitute the values in the equation
1 gram = 0.00220462 pounds
500 grams = 500 × 0.00220462
Multiply the numbers
= 1.1023 pounds ( rounded to four decimal places )
Therefore, 250 grams is 0.5511 pounds
Learn more about conversion factor here
brainly.com/question/23718955
#SPJ4
7. According to Maryland Motor Vehicle Administration [MVA] data, Gary Turgeon, a clerk at the Beltsville, Maryland, MVA location, assists three customers per hour, on average. a. Determine the probability the amount of time Gary takes to assist the next customer is between 6 and 12 minutes (in the interval 6 to 12 minutes). b. Determine the probability the amount of time Gary takes to assist the next customer is between 26 and 35 minutes (in the interval 26 to 35 minutes). c. Determine the probability the amount of time Gary takes to assist the next customer is either less than 14 minutes or greater than 24 minutes.
Answers
The probability that the amount of time Gary takes to assist the next customer is:
a) between 6 and 12 minutes is approximately 0.4168.b) between 26 and 35 minutes is approximately 0.0404.c) either less than 14 minutes or greater than 24 minutes is approximately 0.6032.How to determine probability?To solve this problem, assume that the time it takes Gary to assist a customer follows an exponential distribution with a rate parameter λ = 1/3 customers per minute (since he assists three customers per hour on average).
a) To determine the probability that the time is between 6 and 12 minutes, calculate the cumulative distribution function (CDF) of the exponential distribution at t = 12 and subtract the CDF at t = 6.
P(6 < X < 12) = F(12) - F(6) = (1 - exp(-λ × 12)) - (1 - exp(-λ × 6))
Substituting λ = 1/3:
P(6 < X < 12) = (1 - exp(-(1/3) × 12)) - (1 - exp(-(1/3) × 6))
= 0.4168.
b) To determine the probability that the time is between 26 and 35 minutes, use the same approach:
P(26 < X < 35) = F(35) - F(26) = (1 - exp(-λ × 35)) - (1 - exp(-λ × 26))
Substituting λ = 1/3:
P(26 < X < 35) = (1 - exp(-(1/3) × 35)) - (1 - exp(-(1/3) × 26))
= 0.0404.
c) To determine the probability that the time is either less than 14 minutes or greater than 24 minutes, calculate the complementary probabilities:
P(X < 14) = 1 - exp(-λ × 14)
P(X > 24) = 1 - F(24) = 1 - (1 - exp(-λ × 24))
Substituting λ = 1/3:
P(X < 14) = 1 - exp(-(1/3) × 14)
P(X > 24) = 1 - (1 - exp(-(1/3) × 24))
= 0.6032
Find out more on probability here: https://brainly.com/question/30390037
#SPJ4
g The college hiking club is having a fund raiser to buy new equipment for fall and winter outings. The club is selling Chinese fortune cookies at a price of $3 per cookie. Each cookie contains a piece of paper with a different number written on it. A random drawing will determine which number is the winner of a dinner for two at a local Chinese restaurant. The dinner is valued at $35. Since fortune cookies are donated to the club, we can ignore the cost of the cookies. The club sold 717 cookies before the drawing. Lisa bought 31 cookies. What is the probability she will win the dinner for two
Answers
To determine the probability that Lisa will win the dinner for two, we need to compare the number of cookies she bought to the total number of cookies sold.
The total number of cookies sold is 717, and Lisa bought 31 cookies. Therefore, the probability that Lisa's cookie will be chosen as the winner depends on the ratio of the number of cookies she bought to the total number of cookies sold.
Probability = Number of Lisa's Cookies / Total Number of Cookies Sold
Probability = 31 / 717
Probability ≈ 0.0432
Therefore, the probability that Lisa will win the dinner for two is approximately 0.0432 or 4.32%.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
out of 5 mathematicians and 7 physicist a complete consisting 2 two mathematicians and three physicist is to form in how many ways can this be done any physicist can be included
Answers
Answer:
What does this mean?
Step-by-step explanation:
......
in analysis of variance, a factor is defined as multiple choice question. a categorical independent variable that explains variation in a response, or dependent, variable. a quantitative dependent variable which has variation that we are attempting to explain. a categorical variable that we are using to determine proportions. a categorical dependent variable which has variation that we are attempting to explain.
Answers
A factor in analysis of variance is defined as a categorical independent variable that explains variation in a response, or dependent, variable.
This means that the factor is a grouping variable that separates the observations into distinct categories or levels that we believe may have an effect on the response variable. The response variable is a quantitative dependent variable which has variation that we are attempting to explain. We use the factor to explain the differences or variability in the response variable. It is important to note that the factor can only explain differences if there is variation in the response variable to begin with. If there is no variation in the response variable, then the factor will not have an effect. In summary, the factor is a categorical variable that we use to explain the variation in a quantitative dependent variable. This is a long answer but I hope it helps clarify the concept of a factor in analysis of variance.
In analysis of variance, a factor is defined as a categorical independent variable that explains variation in a response, or dependent, variable.
To know more about variance visit :-
https://brainly.com/question/20038903
#SPJ11
Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line, using the disk/washer method. Sketch the region, the solid, and a typical disk or washer.y = (x - 2)^2 ; y=2x-1 ; about the line y = -1
Answers
Check the picture below.
to check where the functions intersect, we can simply set them equal to each other so (x-2)² = 2x - 1, anyhow, not to bore you to death with that, it's as the picture shows it, at x = 1 and x = 5, so those are our bounds.
to get the R² part of the washer, what I do is using the "area under the curve" method of f(x) - g(x), where g(x) is the axis of rotation and f(x) is the farthest radius, so to get R² I'd process (x-2)² - (-1), that'd give me R and then I'd square that.
to get r², I do pretty much the same thing, f(x) - g(x) where g(x) is the axis of rotation and f(x) is the closest radius, in this namely (2x - 1) - (-1), and that'd give "r" and then we can square that to get r².
\(\begin{cases} R = 2x\\ r = x^2-4x+5 \end{cases}\hspace{5em} \begin{array}{llll} \stackrel{R^2}{4x^2}~~ - ~~\stackrel{r^2}{(x^4-8x^3+26x^2-40x+25)} \\\\\\ -x^4+8x^3-22x^2+40x-25 \end{array} \\\\[-0.35em] ~\dotfill\\\\ \displaystyle \pi \int\limits_{1}^{5}(-x^4+8x^3-22x^2+40x-25)dx \\\\\\ \pi \left[ -\cfrac{x^5}{5}+2x^4-\cfrac{22x^3}{3} +20x^2-25x\right]_{1}^{5}\implies \cfrac{1408\pi }{15}\)

simplify: 5w(1-8h)+12hw+5w+3-w
Answers
Answer:
−28hw+9w+3
Step-by-step explanation:
5w(1-8h) = 5w-40wh
+12wh = -28hw
-28hw+5w+5w = -28hw+10w
-w = -28hw+9w
+3 = -28hw+9w+3