Kayla and her children went into a restaurant and she bought $63 worth of hotdogs and tacos. Each hotdog costs $3.50 and each taco costs $4. She bought 3 more hotdogs than tacos. Write a system of equations that could be used to determine the number of hotdogs and the number of tacos that Kayla bought. Define the variables that you use to write the system.
Answers
Answer:
x= hotdogs
y=tacos
Step-by-step explanation:
(3.50)x+ 3x + 4y= 63
Related Questions
Which expression is equivalent to 8-(6r+2)
Answers
Answer: The expression 8-(6r+2) is equivalent to 8-6r-2.
When you subtract 6r + 2 from 8, you first subtract 2 from 8, which gives you 6. Then you subtract 6r from 6, which gives you 8-6r.
So 8-(6r+2) = 8-6r-2 = 8-6r
Step-by-step explanation:
The table shows the relationship between the diameter in kilometers of an oil spill and the time in days. A quadratic function can be used to model this relationship.What is the best prediction of the time required for the oil spill to reach a diameter of 10 km?

Answers
We can use the general form of a quadratic model:
\(y=ax^2+bx+c\)We can find the parameters a, b and c by taking some pair of values from the table, like this:
Let's take the pair (0,0), if we replace these values for y and x into the above model we get:
\(\begin{gathered} 0=a\times(0)^2+b\times(0)+c \\ 0=c \\ c=0 \end{gathered}\)Now let's take the pair (1, 2.4), by replacing these values into the above model for x and y, we get:
\(\begin{gathered} 2.4=a\times(1)^2+b\times(1) \\ 2.4=a+b \end{gathered}\)From this equation, we can solve for a to get:
\(\begin{gathered} 2.4=a+b \\ 2.4-b=a+b-b \\ a=2.4-b \end{gathered}\)By taking the pair (2, 9.4) we get:
\(\begin{gathered} 9.4=a(2)^2+b\times2 \\ 9.4=4a+2b \end{gathered}\)We can replace the expression that we got previously a = 2.4 - b into the above equation to get:
\(9.4=4(2.4-b)+2b\)From this expression, we can solve for b like this:
\(\begin{gathered} 9.4=4(2.4-b)+2b \\ 9.4=9.6-4b+2b \\ 9.4-9.6=9.6-9.6-2b \\ -0.2=-2b \\ -2b=-0.2 \\ b=\frac{-0.2}{-2} \\ b=0.1 \end{gathered}\)Now we can replace it into the equation a = 2.4 - b, then we get:
a = 2.4 - 0.1 = 2.3
Then we get the expression:
\(y=2.3x^2+0.1x\)Now we just have to evaluate 10 km into the equation, then we get:
\(y=2.3\times(10)^2+0.1\times(10)=231\)Then, the best prediction of the time required for the oil spill to reach a diameter of 10 km is 233 days
Suppose we have the following data given to us in this table. Given this data, we would expect the quality of life to have increased by what percentage over the last 10 years on average? Answer this as a percentage and round your answer to two digits after the decimal without the percentage sign. ex. If you found the rate to be 5.125%, answer 5.13.
Answers
The quality of life has increased by an average percentage of X.XX% over the last 10 years.
To calculate the percentage increase in the quality of life over the last 10 years, we can use the formula:
Percentage Increase = [(Final Value - Initial Value) / Initial Value] * 100
1. Identify the initial value and the final value: Look at the data table provided and determine the initial quality of life value and the final quality of life value over the 10-year period.
2. Calculate the difference between the final and initial values: Subtract the initial quality of life value from the final quality of life value.
3. Divide the difference by the initial value: Divide the difference obtained in step 2 by the initial quality of life value.
4. Multiply by 100 to get the percentage: Multiply the result from step 3 by 100 to obtain the percentage increase.
5. Round the percentage to two decimal places: Round the percentage to two digits after the decimal point, as instructed in the question.
By following these steps and performing the calculations using the given data, you will determine the average percentage increase in the quality of life over the last 10 years.
To learn more about percentage, click here: brainly.com/question/24877689
#SPJ11
Solve the differential equation (Show your work). \[ 7 x^{6} \cos y d x-d y=0 \]
Answers
The solution to the given differential equation is: x⁷ cos y = y + C
where C is the constant of integration
To solve the given differential equation:
\(\[7x^6\cos y dx - dy = 0\]\)
We can separate the variables and integrate both sides.
Separating variables, we can write the equation as:
\(\[7x^6\cos y dx = dy\]\)
Now, we can integrate both sides with respect to their respective variables:
\(\[\int 7x^6\cos y dx = \int dy\]\)
Integrating the left side:
\(\[\int 7x^6\cos y dx = 7 \int x^6 \cos y dx\]\)
To integrate \(\(x^6 \cos y\)\)with respect to x, we can use integration by parts.
Let's take u = x⁶ and \(\(dv = \cos y dx\)\).
Differentiating u with respect to \(\(x\) gives \(du = 6x^5 dx\).\)
Integrating dv with respect to x gives \(\(v = \int \cos y dx = \cos y \cdot x\).\)
Applying the integration by parts formula:
\(\[\int x^6 \cos y dx = u \cdot v - \int v \cdot du\]\)
Substituting the values:
\(\[\int x^6 \cos y dx = x^6 \cdot \cos y \cdot x - \int (\cos y \cdot x) \cdot (6x^5 dx)\]\)
Simplifying:
\(\[\int x^6 \cos y dx = x^7 \cos y - 6 \int x^6 \cos y dx\]\)
Moving the integral term to the left side:
\(\[7 \int x^6 \cos y dx = x^7 \cos y\]\)
Dividing both sides by 7:
\(\[\int x^6 \cos y dx = \frac{x^7 \cos y}{7}\]\)
Now, substituting this result back into our original equation:
\(\[7 \int x^6 \cos y dx = dy\]\)
\(\[\frac{7x^7 \cos y}{7} = dy\)
Simplifying:
x⁷ cos y = dy
Finally, the solution to the given differential equation is:
x⁷ cos y = y + C
where C is the constant of integration.
To learn more about differential equations visit:
brainly.com/question/25731911
#SPJ11
PLS HELP
Given the following diagram, find the required measures.
Given: l || m
m∠1=120
m∠3=40
m∠4=
120
50
140

Answers
definition of a supplementary angle:
angles that when added together, equal 180.
Hera are 4 fractions labelled A,B,C and D 3/4 5/6 16/25 9/15 A B C D Write them in order starting from the smallest
Answers
Answer: 9/15, 16/25, 3/4 and 5/6.
Step-by-step explanation:
From the question, we have been given four fractions which are 3/4, 5/6, 16/25 and 9/15. We are told to write them in order starting from the smallest. For this to be done, we will have to change the fractions to percentages. This will be:
3/4 = 3/4 × 100 = 75%
5/6 = 5/6 × 100 = 83.3%
16/25 = 16/25 × 100 = 64%
9/15 = 9/15 × 100 = 60%
From the above percentages, arranging the fractions from the smallest will be:
9/15, 16/25, 3/4 and 5/6.
Two numbers are given below.
34,856
39,670
a) Approximate the sum of these numbers
by first rounding each number to the
nearest hundred.
b) Find the exact sum of these numbers,
then round this value to the nearest
hundred.
Answers
a) The approximate sum of the numbers by first rounding each number is 74,600
b) The exact sum of the numbers rounded to the nearest hundred is 74,500
From the question, we are determine the approximate sum of the given numbers
The given numbers are
34,856 and 39,670
a) Round 34,856 to the nearest hundred
34,856 to the nearest hundred is 34,900
Also,
Round 39,670 to the nearest hundred
39,670 to the nearest hundred is 39,700
Now,
Add the rounded numbers
34,900 + 39,700 = 74,600
b) The exact sum of the numbers is
34,856 + 39,670 = 74,526
Rounding the result to the nearest hundred
74,526 rounded to the nearest hundred is 74,500
Hence, the exact sum of the numbers rounded to the nearest hundred is 74,500
Learn more on Addition of numbers here: https://brainly.com/question/3026759
#SPJ1
This graph represents the positions of two turtles in a race.On the same axes, draw a line for a third turtle that is going half as fast as the turtle described by line g.
Answers
Answer:
step g
Step-by-step explanation:
it axis is giong up more than other turtle which makes more sense.
cpt-memorial is normally distributed with a mean of 23 minutes and a standard deviation of 10 minutes. what is the z-score for a 34 minute wait?
Answers
The z-score for a 34-minute wait time in the cpt-memorial distribution is 1.1.
The z-score is a measure of how many standard deviations away from the mean a particular value falls. It is calculated by subtracting the mean from the value of interest and then dividing by the standard deviation.
In this case, we want to find the z-score for a 34 minute wait when the mean is 23 minutes and the standard deviation is 10 minutes.
z = (34 - 23) / 10
z = 1.1
So the z-score for a 34 minute wait is 1.1. This means that a 34 minute wait is 1.1 standard deviations above the mean wait time for cpt-memorial.
We can use this z-score to determine the percentage of wait times that fall below or above 34 minutes by using a standard normal distribution table. For example, a z-score of 1.1 indicates that approximately 86.42% of wait times are below 34 minutes, while 13.58% of wait times are above 34 minutes.
Overall, the z-score is a useful tool for understanding how a particular value relates to the distribution of a dataset.
for more questions on z-score
https://brainly.com/question/25638875
#SPJ11
if a super set Y involves a proper subset x......is that, the proper subset x, integral, to Y as a superset? or can Y as superset Y be without a proper subset in the set superset Y?
Answers
Whenever a set X is a subset of set Y, we say the Y is a superset of X and we write, Y ⊇ AX.
Symbol ⊇ is used to denote ‘is a super set of’
find the angles of this

Answers
Angles of ∠y is 45° and ∠x is 135°.
What are angles?An angle is a figure in Euclidean geometry made up of two rays that share a common terminal and are referred to as the angle's sides and vertices, respectively. Angles created by two rays are in the plane where the rays are located. The meeting of two planes also creates angles. We refer to these as dihedral angles.
Given Data
SRQ = 130°
∠R = 130°
As PR is the same line
So. angles of the line is 180°.
∠Y + ∠R = 180
∠y = 180 - 135
∠y = 45°
Now, PQ is the straight line
∠y +∠x = 180
∠x = 180-45
∠x = 135°
Angles of ∠y is 45° and ∠x is 135°.
To learn more about angles, visit:
https://brainly.com/question/28451077
#SPJ13
five times a number is 120
Answers
Answer: The Number is 24.
Step-by-step explanation:
1) Set unknown number to a variable (I'm going to do x).
2) Set up equation: 5x = 120.
3) Simplify by dividing both sides by 5: 5x/5 = 120/5 = 24.
f(x) = (-9-3x)(x+4). Is this equation in factored form? If not, how do you convert it to that form?
Answers
The equation f(x) = (-9 - 3x)(x + 4), as represented is in its factored form
Checking if the equation is in factored form?From the question, we have the following parameters that can be used in our computation:
f(x) = (-9-3x)(x+4)
Express properly
f(x) = (-9 - 3x)(x + 4)
The above equation is a quadratic function
As a general rule, a quadratic function in factored form is represented as
f(x) = (ax + b)(cx + d)
When the equation are compared, we have
a = -3, b = -9
c = 1 and d = 4
This means that the equation f(x) = (-9 - 3x)(x + 4) is in factored form
Read more about quadratic function at
https://brainly.com/question/25841119
#SPJ1
Examine Carmen's plans for rail lines at a train station.
2
(6x + 5)°
X
48%
What is the measure of angle 2? m/2 =
K
m
(7x-4)°
t
Answers
The measure of angle 2 is 73.
What is angle?An angle is a combination of two rays (half-lines) with a common endpoint.
Given:
As, angle 1 and 2 are supplementary
<1 + <2 + (6x +5) =180
And, by corresponding angle, <1= 48
So, 48 + <2 + (6x +5)= 180
<2 + (6x +5) = 132
Also x= 9
then, <2 = 132 - 59
<2= 73.
Hence, measure of <2 is 9.
Learn more about this concept here:
https://brainly.com/question/16198083
#SPJ1
In the largest clinical trial ever conducted, 401,974 children were randomly assigned to two groups. The treatment group consisted of 201,229 children given the Salk vaccine for polio, and the other 200,745 children were given a placebo. Among those in the treatment group, 33 developed polio, and among those in the placebo group, 115 developed polio. If we want to use the methods for testing a claim about two population proportions to test the claim that the rate of polio is less for children given the Salk vaccine, are the requirements for a hypothesis test satisfied?a. The requirements are satisfied; the samples are simple random samples that are independent, and for each of the two groups, the sample size is at least 1000.b. The requirements are not satisfied; the difference between the rates of those that developed polio in the two groups is not statistically significant.
Answers
The requirements for a hypothesis test are satisfied.
To test the claim that the rate of polio is less for children given the Salk vaccine, we need to check if the requirements for a hypothesis test about two population proportions are met. The requirements are:
1. The samples are simple random samples and independent.
2. For each of the two groups, the sample size is at least 1000.
In this case, the study involved 401,974 children who were randomly assigned to two groups: the treatment group with 201,229 children and the placebo group with 200,745 children. This satisfies the first requirement, as the samples are simple random samples and independent. The sample size for both groups is also larger than 1000, meeting the second requirement.
Therefore, the requirements for a hypothesis test are satisfied, and we can proceed with testing the claim that the rate of polio is less for children given the Salk vaccine.
To know more about proportions, visit
https://brainly.com/question/30657439
#SPJ11
gement System Grade 0.00 out of 10.00 (0%) Plainfield Electronics is a New Jersey-based company that manufactures industrial control panels. The equation gives the firm's production function Q=-L³+15
Answers
The equation Q = -L³ + 15 represents the production function of Plainfield Electronics, where Q is the quantity of industrial control panels produced and L is the level of labor input.
In this production function, the term -L³ indicates that there is diminishing returns to labor. As the level of labor input increases, the additional output produced decreases at an increasing rate. The term 15 represents the level of output that would be produced with zero labor input, indicating that there is some fixed component of output. To maximize production, the firm would need to determine the optimal level of labor input that maximizes the quantity of industrial control panels produced. This can be done by taking the derivative of the production function with respect to labor (dQ/dL) and setting it equal to zero to find the critical points. dQ/dL = -3L². Setting -3L² = 0, we find that L = 0.
Therefore, the critical point occurs at L = 0, which means that the firm would need to employ no labor to maximize production according to this production function. However, this result seems unlikely and may not be practically feasible. It's important to note that this analysis is based solely on the provided production function equation and assumes that there are no other factors or constraints affecting the production process. In practice, other factors such as capital, technology, and input availability would also play a significant role in determining the optimal level of production.
To learn more about Plainfield click here: brainly.com/question/30135800
#SPJ11
ou go to the doctor and he gives you 11 milligrams of radioactive dye. after 20 minutes, 5.5 milligrams of dye remain in your system. to leave the doctor's office, you must pass through a radiation detector without sounding the alarm. suppose the detector will sound the alarm if more than 2 milligrams of the dye are in your system. how long will your visit to the doctor take, assuming you were given the dye as soon as you arrived? give your answer to the nearest minute.
Answers
Suppose the detector will sound the alarm if more than 2 milligrams of the dye are in your system. It will take 56 minutes for the visit of the doctor
The amount of radioactive dye remaining in your system after t minutes can be modeled as:
A(t) = 11 * (1/2)^(t/20)
where A(t) is the amount of dye remaining after t minutes. We want to find the time t when A(t) = 2 milligrams.
A(t) = 11 * (1/2)^(t/20) = 2
Solving for t:
(1/2)^(t/20) = 2/11
Taking the natural logarithm of both sides:
(t/20) = ln(2/11) / ln(1/2)
Multiplying both sides by 20:
t = 20 * ln(2/11) / ln(1/2)
Using a calculator or logarithm tables, we can estimate t to be approximately 56 minutes. So, your visit to the doctor would take about 56 minutes.
To learn more about logarithm click on,
https://brainly.com/question/28081645
#SPJ4
6. You are flying a kite and have let out 80 m of string. The kite's angle of elevation with the ground is 40°. If the string is stretched straight, how high is the kite above the ground?
Answers
To find out how high the kite is above the ground, we need to use trigonometry. Specifically, we can use the tangent function since we have the opposite and adjacent sides of a right triangle.
First, let's label the triangle. The kite is at the top, and the ground is at the bottom. The string is the hypotenuse of the triangle, and the height of the kite is the opposite side. The angle of elevation is the angle between the string and the ground, so it is the angle opposite the height.
Using the tangent function, we get:
tan(40°) = opposite/80m
To solve for the height, we can rearrange the formula:
opposite = 80m * tan(40°)
opposite = 80m * 0.839
opposite = 67.1m
Therefore, the kite is approximately 67.1 meters above the ground. It's important to note that this answer is an approximation since the kite may not be perfectly vertical and other factors could affect the height. Nonetheless, the calculation gives us a good estimate of how high the kite is flying.
Learn more about trigonometry here:
https://brainly.com/question/15274772
#SPJ11
Find em when em = 7x and the midpoint is m and mg = 8x-6

Answers
Answer:
EM = 42
Step-by-step explanation:
If M is the midpoint, then we can say that EM = MG.
So now, I can set up an equation:
7x = 8x - 6
And solve for x.
7x = 8x - 6
-8x -8x
-x = -6
x = 6
Since we are trying to find EM, and EM is 7x, we can multiply x by 7 to find our answer:
7x
7(6)
42
EM = 42
Guys can you please help. I dont understand. Thank you. :))))
Lines AB and CD intersect at E. If the measure of angle AEC=5x-20 and the measure of angle BED=x+50, find, in degrees, the measure of angle CEB.
Answers
Answer: 112.5
Step-by-step explanation: When line AB and CD intersect at point E, angle AEC equals BED so you set them equal to each other and find what x is. 5x -20 = x + 50, solving for x, which gives you 17.5. Finding x will tell you what AEC and BED by plugging it in which is 67.5. Angle BED and BEC are supplementary angles which adds up to 180 degrees. So to find angle CEB, subtract 67.5 from 180 and you get 112.5 degrees.
14. Una empresa necesita 2500 focos. En una tienda compran 2/5 partes y en otra 2/10 partes. ¿Cuántos focos ha comprado la empresa?
Answers
The company purchased 2000 light bulbs, buying 2/5 of the quantity at one store and 2/10 of the quantity at another store.
The company needed to purchase 2500 light bulbs. They bought 2/5 of that quantity at one store and 2/10 of that quantity at another store. To calculate how many bulbs the company bought, we can use the formula for adding fractions with the same denominator:
A/B + C/B = (A+C)/B
In this case, A = 2, B = 5, and C = 2. Applying the formula, we get:
2/5 + 2/5 = (2+2)/5 = 4/5
Therefore, the company bought 4/5 of 2500, or 2000 light bulbs.
Learn more about fractions here:
https://brainly.com/question/30340112
#SPJ1
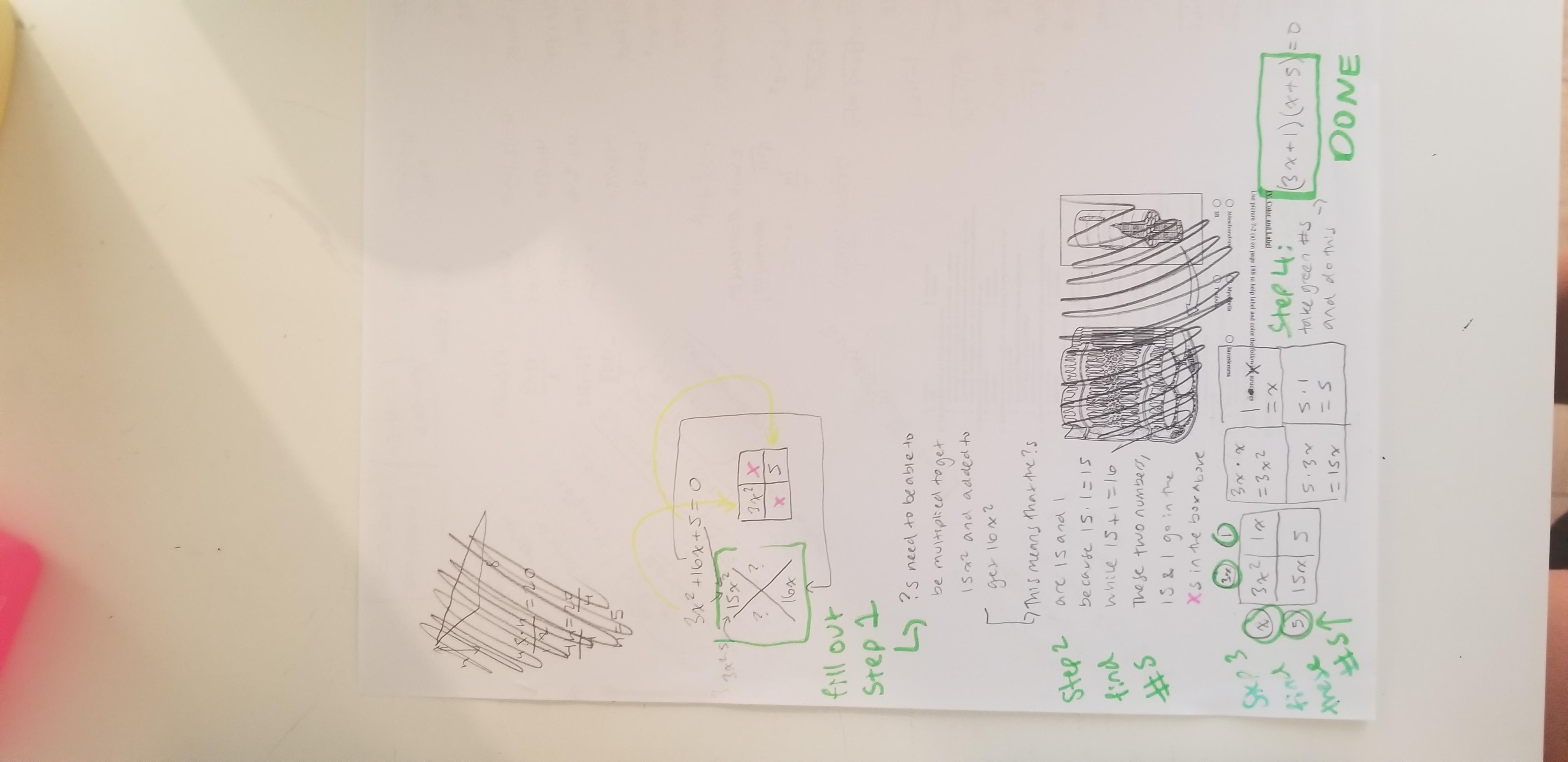
solve: 3x^2+16x+5=0
I did it but apparently its wrong so, please help it would literally probably help me finish high school.
Answers
Answer:
(3x+1)(x+5)
Step-by-step explanation:
Sorry for my handwriting lol hope this makes sense
find the differential dy of the given function. y = csc 6x
Answers
The differential dy of the given function y = csc(6x) is dy = -6csc(6x)cot(6x)dx.
To find the differential dy, we first need to find the derivative of the function y with respect to x. We will use the chain rule and the derivative of the cosecant function in this process.
Step 1: Identify the inner function.
In this case, the inner function is 6x.
Step 2: Identify the outer function.
The outer function is csc(u), where u is the inner function.
Step 3: Find the derivative of the inner function.
The derivative of 6x with respect to x is 6.
Step 4: Find the derivative of the outer function.
The derivative of csc(u) with respect to u is -csc(u)cot(u).
Step 5: Apply the chain rule.
dy/dx = (derivative of outer function) * (derivative of inner function)
dy/dx = (-csc(u)cot(u)) * 6
Step 6: Replace u with the inner function.
dy/dx = (-csc(6x)cot(6x)) * 6
Step 7: Simplify the expression.
dy = -6csc(6x)cot(6x)dx
So, the differential dy of the given function y = csc(6x) is dy = -6csc(6x)cot(6x)dx.
To know more about differential refer here:
https://brainly.com/question/24898810
#SPJ11
Find the lenght of side BC. give your answer to 3 significant figures

Answers
Answer:
BC ≈ 19.4 cm
Step-by-step explanation:
Using the cosine ratio in the right triangle
cos71° = \(\frac{adjacent}{hypotenuse}\) = \(\frac{AB}{BC}\) = \(\frac{6.3}{BC}\) ( multiply both sides by BC )
BC × cos71° = 6.3 ( divide both sides by cos71° )
BC = \(\frac{6.3}{cos71}\) ≈ 19.4 cm ( to 3 significant figures )
BRAINLIEST EASY 6TH GRADE MATH HELP PLS (decimals)

Answers
1
0.95
0.9
0.71
0.7
0.5
0.07
Smallest (least)
Josh mixes blue and white paint to make a lighter shade of white. He needs the ratio of blue to white paint to be 3:2 to get the desired color. If he uses 15 drops of blue paint, how many drops of white paint does he need to use
Answers
Answer:
15 drops of blue to 10 drops of white paint.
Step-by-step explanation:
multiply 3 by 5 to get 15
multiply 2 by 5 to get 10
so 10 drops of white paint.
Someone please help I really appreciate it

Answers
Answer:
The 12 represents the length by width (the 4 by 3).
The 5 represents the height of the figure.
We would use 12 x 5 if we wanted to find the volume. (W x L x H)
What is the area, in square meters, of the trapezoid below?

Answers
Step-by-step explanation:
A = 1/2*h(base + base)
Plugging everything in gives you:
1/2*(6.8)(7.5 + 13.7 + 5.3)
((13.7 + 5.3) gives you the bottom base)
First, adding inside the parentheses:
1/2*(6.8)(26.5)
Multiply 6.8 by 26.5(h times bases):
1/2*(180.2)
Lastly, multiply:
A= 90.1 m^2
Hope this helps :)
Solve: startfraction 2 over 3 endfraction minus 4 x plus startfraction 7 over 2 endfraction equals negative 9 x plus startfraction 5 over 6. endfraction. â€"" 4x = â€""9x x = x equals negative startfraction 3 over 2 endfraction. x = x equals negative startfraction 2 over 3 endfraction. x = x equals startfraction 2 over 3 endfraction. x = x equals startfraction 3 over 2 endfraction.
Answers
The solution to the equation is x = -2/3.
To solve the equation:
(2/3) - 4x + (7/2) = -9x + (5/6)
We can simplify it by combining like terms:
-4x + (7/2) = -9x + (5/6) - (2/3)
To eliminate the fractions, we can multiply every term by 6 to get rid of the denominators:
6 * (-4x) + 6 * (7/2) = 6 * (-9x) + 6 * (5/6) - 6 * (2/3)
Simplifying further:
-24x + 21 = -54x + 5 - 4
Combining like terms:
-24x + 21 = -54x + 1
To isolate the variable x, we can bring all terms containing x to one side and the constant terms to the other side:
-24x + 54x = 1 - 21
30x = -20
Finally, we solve for x by dividing both sides of the equation by 30:
x = -20/30
Simplifying the fraction:
x = -2/3
Learn more about equation here: https://brainly.com/question/29538993
#SPJ11
A rainwater system is structured as shown. The radii are the same for both rain barrels. The shorter rain barrel has a height equal to its radius. The
taller rain barrel has a height twice its radius. The total surface area for both barrels with no top is about 40,212 square centimeters.
Answers
The radius is 1,264 cm
What is the total Surface Area of Cylinder ?The area of the two circular bases and the area of the curving surface together make up the cylinder's total surface area. The area of the circular top and base, as well as the curved surface area, are included in the overall surface area (CSA).
According to the given information
Let radius = r
Height of shorter rain barrel \(h_{1}\) = r
Height of taller rain barrel \(h_{2}\) = 2r
We know that
Each Barrel is a cylinder without top
So
Total Surface area for each = 2\(\pi\)rh + \(\pi\)\(r^{2}\)
TSA for both Barrels = \(2\pi rh_{1} + \pi r^{2}+ 2\pi rh_{2} + \pi r^{2}\)
= \(2 \pi r^{2} + 2\pi r^{2} + 4\pi r^{2}\) ( put \(h_{1}\) = r , \(h_{2}\) = 2r )
= \(8\pi r^{2}\)
r = \(\sqrt{\frac{TSA}{8\pi } }\)
Total surface area is 40 ,212 \(cm^{2}\)
r = \(\sqrt{\frac{40,212}{8\pi } }\)
So
The radius is 1,264 cm
To know more about Surface Area
https://brainly.com/question/29298005
#SPJ1
Answer: cylinder , 20
Step-by-step explanation: