Kathleen made 29, 38, 45, 42, and 36 points on her assignments. What is the mean number of points Kathleen made?
Answers
The mean number of points Kathleen made is 38.
To calculate the mean number of points Kathleen made, we will use the following terms: mean, sum, and total number of assignments.
The mean is the average value of a set of numbers. To find the mean, we need to sum all the given values and then divide the sum by the total number of values in the set.
Kathleen's assignment scores are 29, 38, 45, 42, and 36 points. To find the sum, we add these numbers together: 29 + 38 + 45 + 42 + 36 = 190 points.
Now, we need to determine the total number of assignments. Kathleen has completed five assignments. So, we will divide the sum of her points (190) by the total number of assignments (5) to find the mean.
Mean = Sum / Total number of assignments
Mean = 190 / 5
Mean = 38
The mean number of points Kathleen made on her assignments is 38 points. This indicates that on average, she scored 38 points per assignment. Calculating the mean gives us a general idea of her performance across all assignments, allowing us to gauge her overall progress.
Learn more about mean here: https://brainly.com/question/19243813
#SPJ11
Related Questions
you take a random of twenty ksu students and find that 16 of them have jobs. what is the probability that you would find exactly 16 out of twenty have jobs if the .50 conjectured by the professor was correct? what is the probability that you would find 16 or more have jobs? what will you say to the professor?
Answers
The probability of exactly 16 students having jobs in the sample is 0.204 and the probability of 16 or more students having jobs in the sample is 0.334.
Let X be the number of KSU students with jobs in a random sample of 20 students. Since each student in the sample can be either employed or not employed, X follows a binomial distribution with parameters n = 20 (the sample size) and p = 0.50 (the probability of a student having a job).
To find the probability of exactly 16 students having jobs in the sample, we can use the binomial probability mass function
P(X = 16) = (20 choose 16) * 0.5^16 * 0.5^(20-16) = 0.204
To find the probability of 16 or more students having jobs in the sample, we can use the cumulative distribution function
P(X ≥ 16) = 1 - P(X < 16) = 1 - ∑(i=0 to 15) (20 choose i) * 0.5^i * 0.5^(20-i) = 0.334
Based on the sample data, it appears that the proportion of KSU students with jobs is higher than the professor's conjectured value of 0.50. However, we cannot conclusively reject the professor's conjecture based on a single sample of 20 students.
We would need to conduct a hypothesis test with appropriate statistical significance level to determine if the difference between the sample proportion and the conjectured value is statistically significant or not.
To know more about probability here
https://brainly.com/question/28813679
#SPJ4
Represent this statement as an equation: The difference of twice a number and 3 is 11.
Answers
Answer:
2x - 3 = 11
Step-by-step explanation:
"difference" means subtraction, so it is subtraction.
"twice a number" simply means 2x, since you do not know what the specified number is, it is x. and the 2 and just making it twice the number.
"Is 11" just means equals 11.
so, 2x - 3 = 11.
hope this helps!
7.) Thazzie solved 5 math problems while Zhaniyah finished all the remaining 8problems. What percent of the math problems was Thazzie able to solve?
Answers
ANSWER:
38.46%
STEP-BY-STEP EXPLANATION:
Given:
Problems solved by Thazzie: 5 problems
Problems solved by Zhaniyah: 8 problems
Which means that there are 13 problems in total.
Therefore, those 5 represent the following percent:
\(\begin{gathered} p=\frac{5}{13}\cdot100 \\ \\ p=38.46\% \end{gathered}\)Therefore, it represents 38.46% of the problems solved by Thazzie
8. true or false: the population parameter will always be between the lower and upper bounds of the confidence interval. 9. true or false: the sample statistic will always be between the lower and upper bounds of the confidence interval.
Answers
The population parameter will always be between lower and upper bounds of the confidence interval. - True, whereas sample statistic will always be between lower and upper bounds of the confidence interval - False
With a certain degree of certainty, the population parameter is anticipated to lie between the lower and higher limits of the confidence interval. The confidence interval, which gives an interval estimate of the unidentified population parameter, is created based on the sample data. The interval's level of confidence shows the amount of ambiguity we are prepared to accept when determining the actual population parameter.
The confidence interval's lower and upper limits may or may not be met by the sample statistic used to compute them. A single point estimate, the sample figure is susceptible to sampling error. On the other hand, based on the observed sample data and the selected degree of confidence, the confidence interval is a range of values that we can be fairly confident includes the true population parameter.
Read more about population parameter on:
https://brainly.com/question/28046080
#SPJ4
what is the shift
y = log(x+4) -3
Answers
The shift of the function y = log(x+4) -3 is 4 units left and 3 units down
How to determine the shiftFrom the question, we have the following parameters that can be used in our computation:
y = log(x + 4)
The above equation is a logarithmic equation
So, the parent function is
y = log(x)
When the parent function is compared to the given function, we have
3 units down and 4 units left
Read more about transformation at
https://brainly.com/question/1548871
#SPJ1
Hey guys since nobody ever helps me and my mom doesn’t I need help on this assiment thanks :)

Answers
A bit string of length 8 is generated at random. Assume that all outcomes are equally likely. What is the probability that the number of 0's in the bit string is different from the number of 1's
Answers
The probability that the number of 0's in a randomly generated bit string of length 8 is different from the number of 1's is 56/256, or 7/32.
To understand why, let's consider the possible combinations of 0's and 1's in an 8-bit string. There are a total of 2^8 = 256 possible outcomes. Out of these, we need to determine the number of outcomes where the number of 0's and 1's is different.
One way to approach this is by counting the number of strings with 4 zeros and 4 ones, and then subtracting it from the total number of outcomes. The number of ways to arrange 4 zeros and 4 ones is given by the binomial coefficient C(8,4) = 70. Thus, there are 70 outcomes where the number of 0's and 1's is equal.
Subtracting this from the total number of outcomes, we get 256 - 70 = 186 outcomes where the number of 0's and 1's is different. Therefore, the probability of having an unequal number of 0's and 1's is 186/256, which simplifies to 7/32, or approximately 21.9%.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
Can someone please help

Answers
Answer: Small Campground: 15 garbage cans
Large Campground: 45 garbage cans
Step-by-step explanation: If there are 40 picnic tables in a small campground, there should be 15 garbage cans. Because 40/8=5 and 5*3=15. If there are 120 picnic tables in a large campground, there should be 45 garbage cans. Because 120/8=15 and 15*3=45
in a frequency distribution for a numerical variable, the total number of intervals in a frequency distribution usually ranges from to .
Answers
The total number of intervals in a frequency distribution for a numerical variable can vary depending on the range and nature of the data, typically ranging from a minimum of 5 to a maximum of 20 intervals.
A frequency distribution is a representation of data that organizes values into intervals or bins and shows the number of occurrences or frequencies within each interval. The choice of the number of intervals depends on the characteristics of the data and the desired level of detail in the distribution. Generally, it is recommended to have at least five intervals to capture the overall pattern of the data. Too few intervals may oversimplify the distribution, while too many intervals may result in excessive detail and difficulty in interpretation.
The maximum number of intervals, often around 20, is determined by the data range and the desired level of granularity. When the range of values is large or the data contains outliers, more intervals may be needed to capture the variations accurately. On the other hand, if the range is small or the data is relatively homogenous, a smaller number of intervals may suffice. Balancing the level of detail with the readability and interpretability of the distribution is essential to effectively communicate the information contained in the data.
Learn more about distribution here:
https://brainly.com/question/29664127
#SPJ11
A frequency distribution for a numerical variable is a statistical tool that groups the data into intervals and counts the frequency of observations within each interval. The total number of intervals typically ranges from 5 to 20. However, the choice of how many intervals to use depends on the total number of observations in the dataset and the need to balance detail with complexity.
Explanation:In the realm of statistics, creating a frequency distribution for a numerical variable is a common task. In a frequency distribution, data is grouped into intervals or classes, and the frequency of observations within each interval is counted. When determining the number of intervals, it often depends on the total number of observations in the dataset.
Typically, the total number of intervals in a frequency distribution may range from 5 to 20. These are rough guidelines though, and the number of intervals you decide upon should best represent the data and make it easier to interpret.
Learn more about Frequency Distribution here:https://brainly.com/question/32438359
#SPJ12
Let u=In(x) and v=ln(y), for x>0 and y>0.. Write In (x³ Wy) in terms of u and v. Find the domain, the x-intercept and asymptotes. Then sketch the graph for f(x)=In(x-3).
Answers
To find ln(x³y) in terms of u and v, we can use the properties of logarithms. ln(x³y) can be rewritten as ln(x³) + ln(y), and using the property ln(a^b) = bˣ ln(a), we have 3ln(x) + ln(y) = 3u + v.
How can ln(x³y) be written in terms of u and v, where u = ln(x) and v = ln(y)?To find ln(x³y) in terms of u and v, we can use the properties of logarithms. ln(x³y) can be rewritten as ln(x³) + ln(y), and using the property ln(a^b) = bˣ ln(a), we have 3ln(x) + ln(y) = 3u + v.
The domain of the function f(x) = ln(x-3) is x > 3, since the natural logarithm is undefined for non-positive values. The x-intercept occurs when f(x) = 0, so ln(x-3) = 0, which implies x - 3 = 1. Solving for x gives x = 4 as the x-intercept.
There are no vertical asymptotes for the function f(x) = ln(x-3) since the natural logarithm is defined for all positive values. However, the graph approaches negative infinity as x approaches 3 from the right, indicating a vertical asymptote at x = 3.
To sketch the graph of f(x) = ln(x-3), we start with the x-intercept at (4, 0). We can plot a few more points by choosing values of x greater than 4 and evaluating f(x) using a calculator.
As x approaches 3 from the right, the graph approaches the vertical asymptote at x = 3. The graph will have a horizontal shape, increasing slowly as x increases. Remember to label the axes and indicate the asymptote on the graph.
Learn more about terms
brainly.com/question/28730971
#SPJ11
how many subsets of {1, 2, 3, 4, 5, 6, 7, 8} of size two (two elements) contain at least one of the elements of {1, 2, 3}?
Answers
There are 42 subsets of size two that contain at least one of the elements of {1, 2, 3}.
There are \(${8\choose2}=28$\) subsets of size two that can be formed from the set {1, 2, 3, 4, 5, 6, 7, 8}.
To count the number of subsets of size two that contain at least one of the elements of {1, 2, 3}, we can use the principle of inclusion-exclusion.
Let A be the set of subsets of size two that contain 1, B be the set of subsets of size two that contain 2, and C be the set of subsets of size two that contain 3. We want to count the size of the union of these three sets, i.e., the number of subsets of size two that contain at least one of the elements of {1, 2, 3}.
By the principle of inclusion-exclusion, we have:
|A ∪ B ∪ C| = |A| + |B| + |C| - |A ∩ B| - |A ∩ C| - |B ∩ C| + |A ∩ B ∩ C|
To calculate the sizes of these sets, we can use combinations. For example, |A| is the number of subsets of size two that can be formed from {1, 2, 3, 4, 5, 6, 7, 8} with 1 as one of the elements. This is equal to \(${3\choose1}{5\choose1}=15$\), since we must choose one of the three elements in {1, 2, 3} and one of the five remaining elements.
Similarly, we have:
|A| = \(${3\choose1}{5\choose1}=15$\)
|B| = \(${3\choose1}{5\choose1}=15$\)
|C| = \(${3\choose1}{5\choose1}=15$\)
|A ∩ B| = \(${2\choose1}{5\choose0}=2$\), since there are two elements in {1, 2} that must be included in the subset, and we can choose the other element from the remaining five.
|A ∩ C| = \(${2\choose1}{5\choose0}=2$\)
|B ∩ C| = \(${2\choose1}{5\choose0}=2$\)
|A ∩ B ∩ C| = \(${3\choose2}=3$\), since there are three elements in {1, 2, 3} and we must choose two of them.
Substituting these values into the inclusion-exclusion formula, we get:
|A ∪ B ∪ C|\(= 15 + 15 + 15 - 2 - 2 - 2 + 3 = 42\)
Therefore, there are 42 subsets of size two that contain at least one of the elements of {1, 2, 3}.
To learn more about subsets visit: https://brainly.com/question/24138395
#SPJ11
A B What is the converse of the following statement? "If I studied for it, then I did well on the exam." "If I did well on the exam, then I studied for it." "If I did not do well on the exam, then I did not study for it."

Answers
Answer:
A
I believe because p→q
q→p
Determine whether the nonhomogeneous system Ax = b is consistent, and if so, write the solution in the form x = xn + xp where xh is a solution of Ax = 0 and xp is a particular solution of Ax = b.
2x - 4y + 5z = 8
-7x + 14y + 4z = -28
3x - 6y + z = 12
Answers
The general solution of non-homogeneous system can be written as:
x = xh + xp = [2t + 1, t, -2s - 2] + [-1, -28, 1]
We can now write the augmented matrix of the system as:
[2 -4 5 8]
[-7 14 4 -28]
[3 -6 1 12]
We can use row reduction to determine whether the system is consistent and to find its solutions.
Performing the row reduction, we get:
[1 -2 0 2]
[0 0 1 -2]
[0 0 0 0]
From the last row of the row-reduced matrix, we can see that the system has a dependent variable, which means that there are infinitely many solutions. We can write the general solution as:
x = x1 = 2t + 1
y = y1 = t
z = z1 = -2s - 2
Here, t and s are arbitrary parameters.
To find a particular solution, we can use any method we like. One method is to use the method of undetermined coefficients. We can guess that xp is a linear combination of the columns of A, with unknown coefficients:
xp = k1[2 -7 3] + k2[-4 14 -6] + k3[5 4 1]
where k1, k2, and k3 are unknown coefficients.
We can substitute this into the system and solve for the coefficients. This gives:
k1 = -1
k2 = -2
k3 = 1
Therefore, a particular solution is:
xp = [-1 -28 1]
So the general solution can be written as:
x = xh + xp = [2t + 1, t, -2s - 2] + [-1, -28, 1]
where t and s are arbitrary parameters.
To know more about non-homogeneous system refer here:
https://brainly.com/question/13720217
#SPJ11
Will give brainliest, thanks, and 5 stars! LOTS OF POINTS! 50 POINTS!
I need help with these questions! Please help me. The choices are all true/false.
Please help me!!!!!!
Please provide in depth explanation too!!

Answers
Answer in order:
False
True
False
False
False
False
False
True
True
Step-by-step explanation:
All of the solutions to the equation\(3x^2 - 12 = 0\)are x = 12 and x = -12
Solve:
Common factor - \(3(x^2-4)=0\)
Divide both sides
\(x^2-4=0\)
Use the quadratic formula
\(x=\sqrt{4,x}=\sqrt{-4\)
x = 2, x = -2
Thus, This is false..
-------------------------------------------------------------------------------------------------------------
There are two unique solutions to the equations (x-3)^2 = 16
one variable in matrix = one possible value.
Therefore, x = 7, x = -1
Hence this is True
-------------------------------------------------------------------------------------------------------------
The solutions for the equation 2(x-3)^2-18 = 0 are x = 6 and x = 0
\(2x^3-18x^2+54x-72=0\)
\(x=5.080084\)
Hence this is false
-------------------------------------------------------------------------------------------------------------
The solutions for the equation 2(x-5)^2-8=0 are x = 7 and x = -7
Add both sides by 8
2(x-5)^2-8+8=0+8
2(x-5)^2=8
(x-5)^2=4
x = 7, x = 3
Hence, this is false
-------------------------------------------------------------------------------------------------------------
The solutions for the equation (x + 3)^2-25 = -8 are x = 2 and x = -8
\((x+3)^2=17\)
\(x=\sqrt{17-3,}=-\sqrt{17}-3\)
Hence this is false.
-------------------------------------------------------------------------------------------------------------
The solutions for the equation 2(2x-1)^2=18 are x = 5 and x = -4
\((2x-1)^2=9\)
x=2, x = -1
Hence this is false.
-------------------------------------------------------------------------------------------------------------
The only solution for equation (2x-1)^2-49=0 is x = 4
\((2x-1)^2=49\)
x = 4, x = -3
Hence, this is false
-------------------------------------------------------------------------------------------------------------
The solutions for the equation 3(x+2)^2 - 3 = 0 are x = -3 and x = -1
\(3(x+2)^2=3\)
\((x+2)^2=1\)
x = -1, x = -3
Hence, this is true
-------------------------------------------------------------------------------------------------------------
The solutions for the equation 5x^2 - 180 = 0 are x = 6 and x = -6
Add 180 to both sides
\(5x^2-180+180=0+180\)
\(5x^2 = 180\)
\(x^2 = 36\)
\(x=\sqrt{36},x=-\sqrt{36}\)
x = 6, x = -6
Hence, this is true.
-------------------------------------------------------------------------------------------------------------
[RevyBreeze]
Someone please help me. I'm stuck
what does 3/4 • 1/2 mean? (i.e. how else can it be said). Give an example of a word problem that is solved by calculating 3/4 • 1/2.
Answers
ps dont pay attention to the units theyre just there for an example
Hailey had 3/4 feet of a ribbon, she wanted to keep 1/2 of it and give 1/2 of it to her friend. How much does each person get?
The answer is 3/8
a rectangular garden is 24 feet long. if you walk diagonally across the garden, you would walk 30 feet. how many feet wide is the garden?
Answers
The width of the garden is 18 feet. In this case, the length of the diagonal of the rectangular garden is the hypotenuse, and the length and width of the garden are the other two sides. Let's denote the width of the garden as "w".
Given:
Length of the garden = 24 feet
Diagonal of the garden = 30 feet
Using the Pythagorean theorem, we can set up the following equation:
\(24^2\) + \(w^2\) = \(30^2\)
Simplifying:
576 + \(w^2\) = 900
Subtracting 576 from both sides:
\(w^2\) = 900 - 576
\(w^2\) = 324
Taking the square root of both sides:
w = √324
w = 18
So, the width of the garden is 18 feet.
Learn more about “ Pythagorean theorem, “ visit here;
https://brainly.com/question/14930619
#SPJ4
we have:24² + w² = 30²Solve the equation:576 + w² = 900Subtract 576 from both sides:w² = 324 Take the square root of both sides:w = √324w = 18So, the width of the rectangular garden is 18 feet.
Using the Pythagorean theorem, we can find the width of the garden. If the length is 24 feet and the diagonal is 30 feet, then the width can be found by taking the square root of (30^2 - 24^2), which is approximately 18.97 feet.
Therefore, the garden is about 18.97 feet wide. We can use the Pythagorean theorem to find the width of the rectangular garden.
The Pythagorean theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
In this case, the diagonal across the garden is the hypotenuse, and the length and width of the garden are the other two sides.
The diagonal is 30 feet, and the length is 24 feet. We need to find the width (w).
The Pythagorean theorem formula is:a² + b² = c²Where 'a' and 'b' are the two shorter sides, and 'c' is the hypotenuse.
In this case, we have:24² + w² = 30²Solve the equation:576 + w² = 900Subtract 576 from both sides:w² = 324Take the square root of both sides:w = √324w = 18So, the width of the rectangular garden is 18 feet.
to learn more about the Pythagorean theorem click here:
brainly.com/question/15624595
#SPJ11
marcella read 100 books over the school year. 60 of the books were mysteries. she said the mysteries equal 0.06 of the total books. is she correct? explain your thinking. describe a model to help support your answer.
Answers
Yes, the mysteries equal 0.06 of the total books.
Marcella said that the mysteries equal 0.06 of the total books.
To check the mysteries equal 0.06 of the total books is correct or not.
We can follow these steps:
1. Identify the total number of books and the number of mysteries: Marcella read 100 books, and 60 of them were mysteries.
2. Calculate the fraction of mysteries: Divide the number of mysteries (60) by the total number of books (100) to find the fraction of mysteries.
3. Compare the fraction with Marcella's claim: If the calculated fraction equals 0.06, then she is correct.
Now let's perform the calculations:
60 mysteries ÷ 100 total books = 0.6
Since 0.6 ≠ 0.06, Marcella's claim that the mysteries equal 0.06 of the total books is incorrect. In reality, mysteries make up 0.6 or 60% of the total books she read.
A model to support this answer could be a pie chart, where the circle represents the 100 books, and the mysteries portion is shaded in. By dividing the circle into 10 equal sections, the mysteries would fill 6 of those sections, which represents 60% of the total books.
Learn more about books here,
https://brainly.com/question/31410086
#SPJ11
It says Find out the value of x

Answers
34) 31
35) 21
Check the last one to make sure it’s right . The first 2 I’m 100% sure they are correct
Answer:
x=31, x=31, x=21.
Step-by-step explanation:
So for number 33, we see that 2x+28=90 degrees so you just simplify the equation to 2x=62, x=31.
For number 34, we see that 4x+56=180 (flat line), so we simplify the equation again and get 4x=124, x=31 degrees.
For number 35, according to the vertical angle theorem, 43=2x+1, so we simplify that too and we get 42=2x, 21=x, x=21.
Which number is a factor of the prime factorization of 60
1. 6
2. 15
3. 9
4. 3
Answers
Answer:
answer is »»»4. 3
Step-by-step explanation:
Use a factor tree to express 60 as a product of prime factors. So the prime factorization of 60 is 2 × 2 × 3 × 5, which can be written as 2 2 × 3 × 5. The actual prime factors of 60 are 2, 3, and 5.
Which expression is equivalent to cos(4x)?
2(2cos2(x) – 1)2 – 1
2cos2(2x) – 1
2cos2(x) – 4
4cos2(x)
Answers
Answer:
the answer is a. 2cos2(x) - 1) 2 -1
Step-by-step explanation:
an easy way to check is to graph every equation and see which ones line up. i did this and a was the right answer :) (edge 2020)
Trigonometric Identities are equalities that utilize trigonometry functions and hold true for all variables in the equation. The correct option is B.
What are Trigonometric Identities?Trigonometric Identities are equalities that utilize trigonometry functions and hold true for all variables in the equation. There are several trigonometric identities relating to the side length and angle of a triangle.
Cos2x is a double angle trigonometric identity because the angle under consideration is a multiple of 2, or the double of x.
Therefore, The expression that is equivalent to cos(4x) is 2cos²(2x) – 1.
Hence, the correct option is B.
Learn more about Trigonometric Identities:
https://brainly.com/question/13094664
#SPJ2
Which finds the solution to the equation represented by the model below?
F
O removing 1 x-tile from each side
O removing 3 unit tiles from the right side
O adding 3 positive unit tiles to each side
O arranging the tiles into equal groups to match the number of x-tiles
Answers
Answer: A. removing 1 x-tile from each side
Step-by-step explanation: To solve the equation represented by the model, we need to remove 3 unit tiles from the right side, since each unit tile represents a value of 1. Then, we need to arrange the tiles into equal groups to match the number of x-tiles. We can see that there are 2 x-tiles and 2 unit tiles on the left side, which means that each x-tile represents a value of 1.
Therefore, the solution is x = 1. Answer choice A.
Find the volume of this sphere.
Use 3 for TT.
V
V [?]ft3
V = Tr3
16ft
![Find the volume of this sphere.Use 3 for TT.VV [?]ft3V = Tr316ft](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/4D1MLXy7APezVY5RZI2Lfv6wmnNsv98V.png)
Answers
Answer:
well the volume of a sphere is V = 4/3 x pie x r3 so the radius is half of the diameter so that would be 8 not going to show work but the answer is 2144.66
Flyer Co. buys back 5102 shares of their $3 par value common stock for $17 per share. The amount debited to the treasury stock account to record the purchase would be $ ___. Enter zero if the treasury stock account should be credited. Show whole numbers only, no commas, decimals, etc. Mark for Review What's This?
Answers
If Flyer Co. buys back 5102 shares of their $3 par value common stock for $17 per share. The amount debited to the treasury stock account to record the purchase would be $ 86,834.
To calculate the amount debited to the treasury stock account, we need to multiply the number of shares bought back by the price per share.
In this case, Flyer Co. buys back 5102 shares at $17 per share.
The amount debited to the treasury stock account is calculated as follows:
Amount = Number of shares bought back * Price per share
Amount = 5102 * $17
Amount = $86,834
Therefore, the amount debited to the treasury stock account to record the purchase would be $86,834.
To learn more about stock click on,
https://brainly.com/question/15712198
#SPJ4
Instructions: Using the image, find the slope of the line. Reduce all fractions and enter using a forward slash (i.e.
"/"). If the slope is undefined, enter "undefined

Answers
Answer:
Δy = 5 Δx = 1
slope = \(\frac{5}{1}\) = 5
Step-by-step explanation:
I need some help in geometry
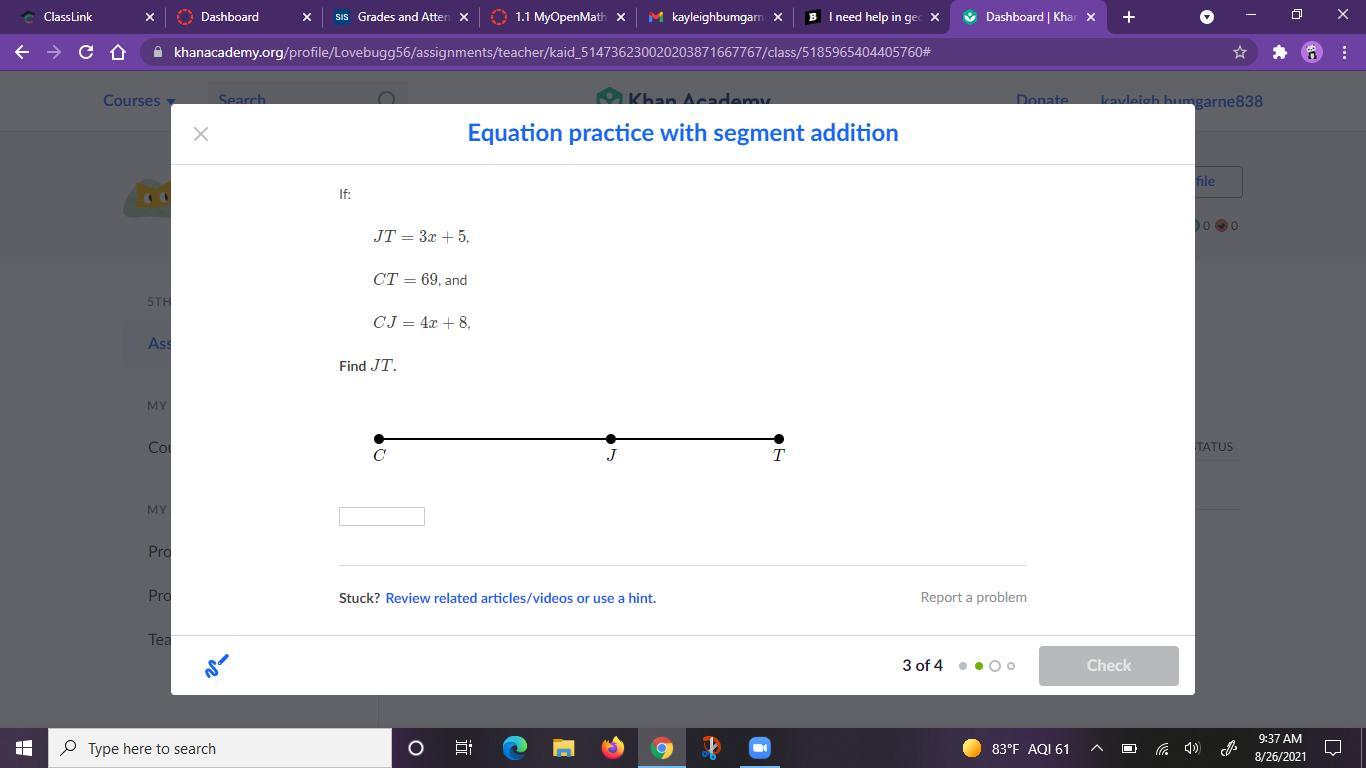
Answers
Answer:
JT = 29
Step-by-step explanation:
CT=CJ+JT
69= (4x+8)+ ( 3x+5)
69= 7x +13
7x= 69-13
7x= 56
x=56/7
x=8
JT=3x+5=3(8)+5= 24+5=29
I hope I helped you^_^
Find the slope of the line.
Give brainiest if correct
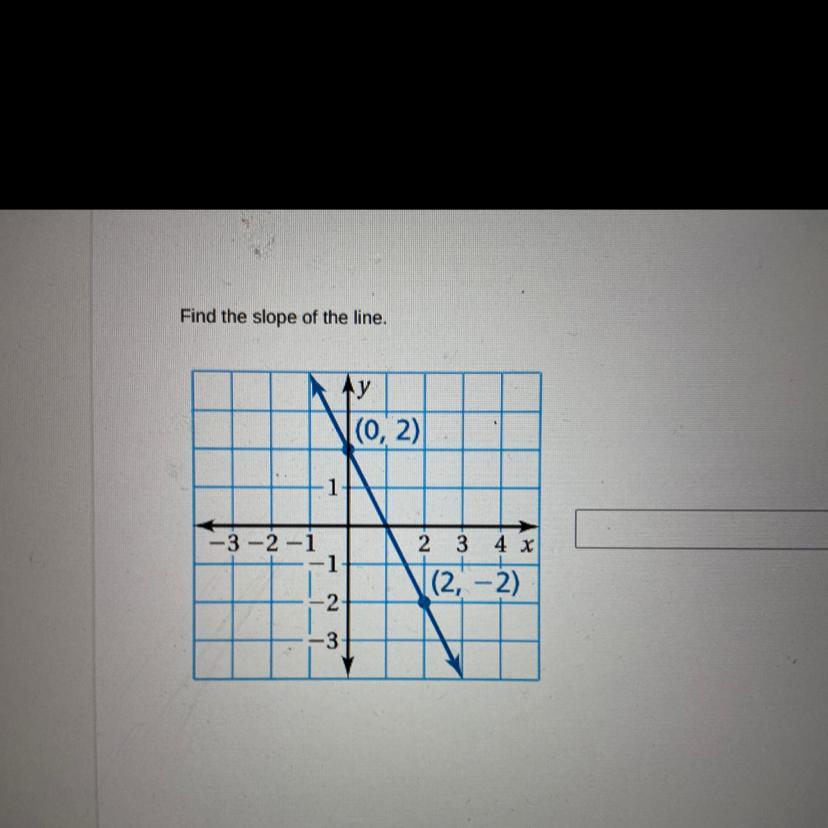
Answers
Answer:
\(m=-2\)
Step-by-step explanation:
\(\left(x_1,\:y_1\right)=\left(0,\:2\right),\:\left(x_2,\:y_2\right)=\left(2,\:-2\right)\)
Answer:
-2 is the answer .
Step-by-step explanation:
Good luck ^^
What is the solution to this equation?
5(x-3) = 21
A x =
OB x=
36
5
D x=
65
6
5
24
OC X= 5
18
5
Answers
Answer:
x = 7.2
Step-by-step explanation:
\(5(x - 3) = 21\)
\(x - 3 = 4.2\)
\(x = 7.2\)
5/7 + 3/8?
1/6 + 5/6?
5/6 + 1/3?
3 4/5 + 7 1/2?
3 3/4 + 5 1/3?
2/3 - 5/8?
3/7 - 1/6?
2/3 - 2/4?
16 2/3 - 12 2/5?
7 5/6 - 3 1/4?
Answers
Answer:
5/7+3/8=40/56+21/56
=61/56=1/5/56
1/6+5/6=6/6=1
5/6+1/3=5/6+2/6
=7/6=1/1/6
3/4/5+7/1/2=19/5+15/2
=38/10+75/10
=113/10=11/3/10
3/3/4+5/1/3=15/4+16/3
=45/12+64/12
=109/12=9/1/12
2/3-5/8=16/24-10/24
=6/24=1/4
3/7-1/6=18/42-7/42
=11/42
2/3-2/4=8/12-6/12
=2/12=1/6
16/2/3-12/2/5=50/3-62/5
=250/15-186/15
=64/15=4/4/15
7/5/6-3/1/4=47/6-13/4
=94/12-39/12
=55/12=4/7/12
The Center for Disease Control and Prevention reports that 25% of bay boys 6-8 months old in the United States weigh more than 20 pounds. A sample of 16 babies is studied.
Answers
Okay, it seems like you want to analyze a sample of 16 babies based on their weight.
The information you provided states that the Center for Disease Control and Prevention reports that 25% of baby boys aged 6-8 months in the United States weigh more than 20 pounds.
However, you haven't mentioned the specific question or analysis you want to perform on the sample. Could you please clarify what you would like to know or do with the given information?
To know more about Prevention visit-
brainly.com/question/30892272
#SPJ11
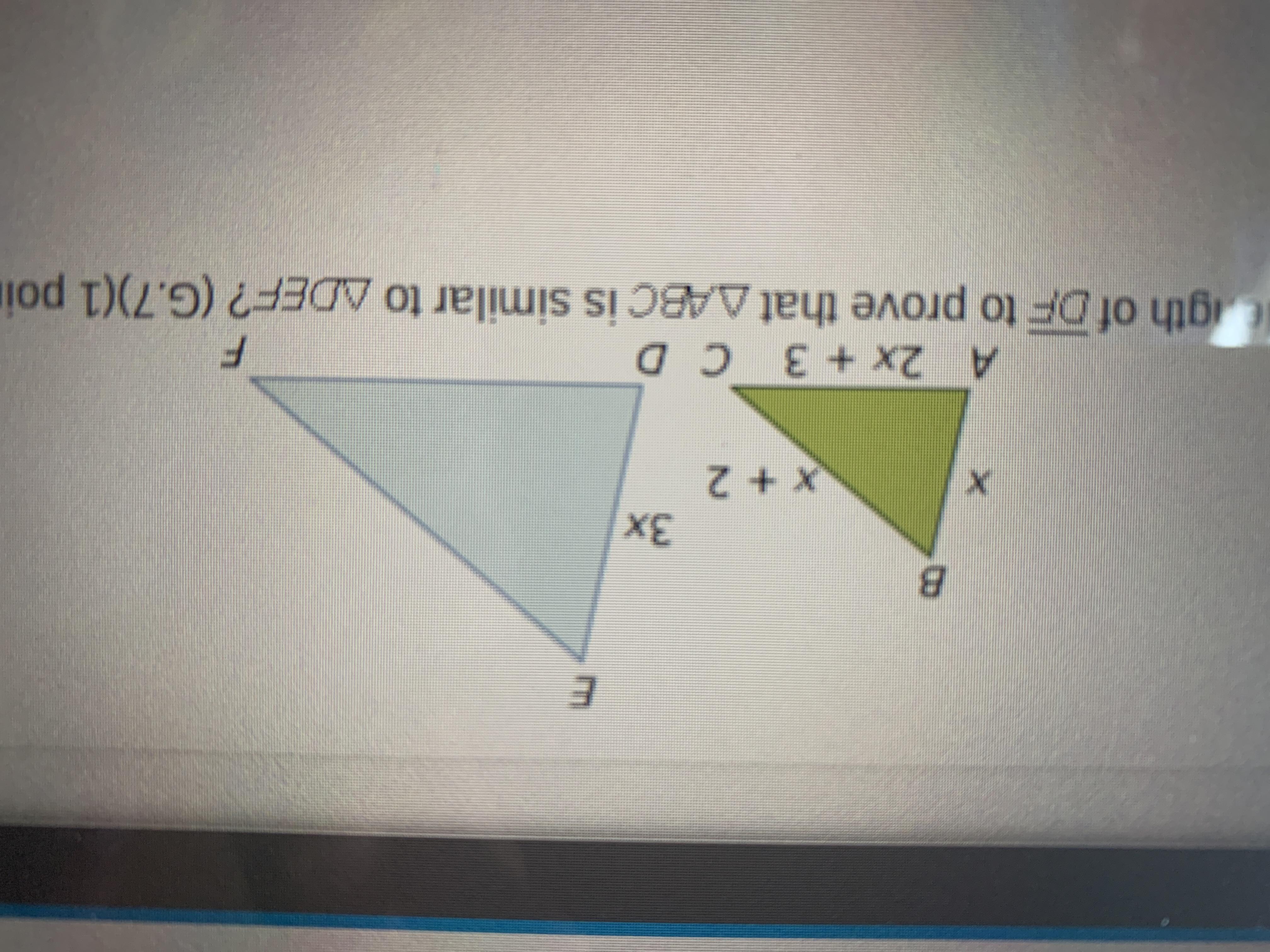
White expression can be used to represent the length of DF to prove that ABC is similar to DEF