Justin paid
$10. 47
for a
6. 08
-
kg
bag of dog food. A few weeks later, he paid
$13. 88
for a
7. 48
-
kg
bag at a different store.
Find the unit price for each bag. Then state which bag is the better buy based on the unit price.
Round your answers to the nearest cent.
Unit price for the
6. 08
-
kg
bag:
$perkg
Unit price for the
7. 48
-
kg
bag:
$perkg
The better buy:The
6. 08
-
kg
bagThe
7. 48
-
kg
bagNeither (They have the same unit price)
Answers
The Unit-Price for first-bag is $1.72/kg and for second-bag is $1.86/kg, then the first-bag is cheaper compared to the second-bag with a unit-price.
The "Unit-Price" refers to the cost of dog food per kilogram. It is calculated by dividing the "total-cost" of the bag of dog-food by its weight in kilograms.
⇒ For the first bag of dog food:
The Cost is = $10.47,
The Weight is = 6.08 kg,
So, the Unit-Price is = Cost/Weight = $10.47/6.08 kg ≈ $1.72/kg,
⇒ For the second bag of dog food:
The Cost is = $13.88,
The Weight is = 7.48 kg,
So, the Unit Price will be = Cost/Weight = $13.88/7.48 kg ≈ $1.86/kg,
Based on the "unit-prices" calculated, the first bag of dog food has a unit price of $1.72 per kilogram, and the second bag has a unit price of $1.86 per kilogram.
Therefore, the first bag of dog food is the better-buy as it is cheaper compared to the second bag.
Learn more about Unit Price here
https://brainly.com/question/29023044
#SPJ4
The given question is incomplete, the complete question is
Justin paid $10.47 for a 6.08-Kg bag of dog food. A few weeks later, he paid $13.88 for a 7.48-kg bag at a different store. Find the unit price for each bag. Then state which bag is the better buy based on the unit price.
Related Questions
M<7=100 find measure of <11
Answers
Answer:i think its 115 degres
Step-by-step explanation:
What is the correct answer?

Answers
Answer:
a
Step-by-step explanation:
simplify
y-(-5) = -(x-7)what is y
Answers
open the parenthesis
y + 5 = -x + 7
subtract 5 from both-side of the equation
y + 5 - 5 = -x + 7 - 5
y = -x + 2
or
y= 2 - x
simplify the expression, and show your work: (4 - 3)^2 x (5 x 4)^0
Answers
Step-by-step explanation:
(4 - 3)^2 x (5 x 4)^0 =
(1)^2 × (20)^0 =
1 × 1 =
1
respusta 1
corazon esterllsa 5
On average, Caryl's school bus arrives on time, although sometimes it is a bit early or late. If the arrival times are distributed on a normal curve, which of the following statistics would enable Caryl to estimate the probability that her bus will arrive within 5 minutes of its scheduled arrival time on any given day?
a. median
b. mean
c. standard deviation
d. correlation coefficient
Answers
If the arrival times of Caryl's school bus are distributed on a normal curve, the standard deviation would enable Caryl to estimate the probability that her bus will arrive within 5 minutes of its scheduled arrival time on any given day.
The standard deviation is a statistic that measures the amount of variation or dispersion from the central tendency of a set of data values. A low standard deviation indicates that the data is tightly clustered around the mean or average, while a high standard deviation indicates that the data is more spread out.
The standard deviation is particularly useful when dealing with normally distributed data, as it allows us to estimate the probability of a certain range of values occurring. In this case, Caryl can use the standard deviation to estimate the probability that her bus will arrive within 5 minutes of its scheduled arrival time on any given day.
Hence, option c. standard deviation would enable Caryl to estimate the probability that her bus will arrive within 5 minutes of its scheduled arrival time on any given day.
To learn more about deviation visit;
https://brainly.com/question/31835352
#SPJ11
What is the vertical change from Point A to Point B?
What is the horizontal change from Point A to Point B?
What is the rate of change shown on the graph? Give
the answer as a decimal rounded to the nearest tenth, if
necessary
Answers
The vertical change from point A to point B is 1. The horizontal change from point A to point B is 2. The rate of change in the graph is 0.5.
What is a graph?A graph is a diametrical representation of any function between the dependent and independent variables.
For example y = x² form a parabola now by looking at only the graph we can predict that it has only a positive value irrespective of the interval of x.
As per the given,
Point A translate to point B on a straight line.
The Coordinate of point A is (2,1).
The Coordinate of point B is (4,2).
Vertical change = 2 - 1 = 1
Horizontal change = 4 - 2 = 2
Slope = vertical change / horizontal change
Slope = 1/2 = 0.5
Hence "The vertical change from point A to point B is 1. The horizontal change from point A to point B is 2. The rate of change in the graph is 0.5".
To learn more about graphs,
brainly.com/question/16608196
#SPJ1
help me with parallel and prependicular please

Answers
parallel option a
its parallel to each other
Sandhill Corporation sells three different models of a mosquito "zapper." Model A12 sells for $60 and has unit variable costs of $42. Model B22 sells for $120 and has unit variable costs of $84. Model C124 sells for $480 and has unit variable costs of $360. The sales mix(as a percentage of total units) of the three models is A12,60\%; B22, 15\%; and C124,25%. What is the weighted-average unit contribution margin? (Round answer to 2 decimal places, es. 15.50.)
Answers
The weighted-average unit contribution margin is $46.20.
The weighted-average unit contribution margin can be calculated by multiplying the unit contribution margin of each model by its respective sales mix percentage, and then summing up the results.
To find the weighted-average unit contribution margin, we first calculate the unit contribution margin for each model by subtracting the unit variable costs from the selling price:
For Model A12:
Unit contribution margin = Selling price - Unit variable cost
= $60 - $42
= $18
For Model B22:
Unit contribution margin = Selling price - Unit variable cost
= $120 - $84
= $36
For Model C124:
Unit contribution margin = Selling price - Unit variable cost
= $480 - $360
= $120
Next, we multiply each unit contribution margin by its respective sales mix percentage:
Weighted contribution margin for Model A12 = 60% * $18 = $10.80
Weighted contribution margin for Model B22 = 15% * $36 = $5.40
Weighted contribution margin for Model C124 = 25% * $120 = $30.00
Finally, we sum up the weighted contribution margins:
Weighted-average unit contribution margin = $10.80 + $5.40 + $30.00 = $46.20. Therefore, the weighted-average unit contribution margin is $46.20.
Learn more about percentage here:
brainly.com/question/32197511
#SPJ11
Need 6 and 7 done please and thank you

Answers
Answer:
black
black
Step-by-step explanation:
If the following data were transformed, and points with the coordinates
(x, log())) were plotted, what points would be plotted? Round log() to three
decimal places.
х
у
4.
81
5 243
6 729
O A. (81, 1.908), (243, 2.386), (729, 2.863)
O B. (4,1.908), (5,2.386)(6,2.863)
O c. (1.908, 4), (2.386,5), (2.863, 6)
O D. (1.908, 81), (2.386, 243), (2.863, 729)

Answers
Answer: B
Step-by-step explanation:
in 2010, $1.00 u.s. bought 8.24 chinese yuan and in 2012 it bought 6.64 chinese yuan. how many u.s. dollars could 1 chinese yuan purchase in 2010 and 2012?
Answers
1 Chinese yuan could purchase $0.12 and $0.15 in the year 2010 and 2012 respectively.
For the year 2010; we can calculate as follows;
1 US dollar = 8.24 Chinese yuan
x US dollar = 1 Chinese Yuan
using cross multiplication to find x;
8.24x = 1 ×1
8.24x = 1
x = 1 / 8.24
x = $0.12
For the year 2012; we can calculate as follows;
1 US dollar = 6.64 Chinese Yuan
x US dollar = 1 Chinese Yuan
Using cross multiplication to find x;
6.64x = 1
x = 1 / 6.64
x = $0.15
Therefore, one Chinese yuan could purchase $0.12 in 2010 and $0.15 in the year 2012.
To learn more about cross multiplication; click here:
https://brainly.com/question/23064464
#SPJ4
solve the differential equation by variation of parameters. y'' + y = cos2(x)
Answers
Answer:
\(y=c_1\cos(x)+c_2\+\sin(x)+\sin^2(x)-\frac{1}{3}\sin^4(x)+\frac{1}{3}\cos^4(x)}}}\)
Step-by-step explanation:
Given the second-order differential equation, \(y'' + y = cos2(x)\), solve it using variation of parameters.
(1) - Solve the DE as if it were homogenous and find the homogeneous solution\(y'' + y = cos2(x) \Longrightarrow y'' + y =0\\\\\text{The characteristic equation} \Rightarrow m^2+1=0\\\\m^2+1=0\\\\ \Longrightarrow m^2=-1\\\\\ \Longrightarrow m=\sqrt{-1} \\\\\Longrightarrow \boxed{m=\pm i} \\ \\\text{Solution is complex will be in the form} \ \boxed{y=c_1e^{\alpha t}\cos(\beta t)+c_2e^{\alpha t}\sin(\beta t)} \ \text{where} \ m=\alpha \pm \beta i\)
\(\therefore \text{homogeneous solution} \rightarrow \boxed{y_h=c_1\cos(x)+c_2\sin(x)}\)
(2) - Find the Wronskian determinant
\(|W|=\left|\begin{array}{ccc}y_1&y_2\\y'_1&y'_2\end{array}\right| \\\\\Longrightarrow |W|=\left|\begin{array}{ccc}\cos(x)&\sin(x)\\-sin(t)&cos(x)\end{array}\right|\\\\\Longrightarrow \cos^2(x)+\sin^2(x)\\\\\Longrightarrow \boxed{|W|=1}\)
(3) - Find W_1 and W_2
\(\boxed{W_1=\left|\begin{array}{ccc}0&y_2\\g(x)&y'_2\end{array}\right| and \ W_2=\left|\begin{array}{ccc}y_2&0\\y'_2&g(x)\end{array}\right|}\)
\(W_1=\left|\begin{array}{ccc}0&\sin(x)\\\cos^2(x)&\cos(x)\end{array}\right|\\\\\Longrightarrow \boxed{W_1= -\sin(x)\cos^2(x)}\\\\W_2=\left|\begin{array}{ccc}\cos(x)&0\\ -\sin(x)&\cos^2(x)\end{array}\right|\\\\\Longrightarrow \boxed{W_2= \cos^3(x)}\)
(4) - Find u_1 and u_2
\(\boxed{u_1=\int\frac{W_1}{|W|} \ and \ u_2=\int\frac{W_2}{|W|} }\)\
u_1:
\(\int(\frac{-\sin(x)\cos^2(x)}{1}) dx\\\\\Longrightarrow-\int(\sin(x)\cos^2(x)) dx\\\\\text{Let} \ u=\cos(x) \rightarrow du=-sin(x)dx\\\\\Longrightarrow\int u^2 du\\\\\Longrightarrow \frac{1}{3}u^3\\ \\\Longrightarrow \boxed{u_1=\frac{1}{3}\cos^3(x)}\)
u_2:
\(\int\frac{\cos^3(x)}{1}dx\\ \\\Longrightarrow \int \cos^3(x)dx\\\\ \Longrightarrow \int (\cos^2(x)\cos(x))dx \ \ \boxed{\text{Trig identity:} \cos^2(x)=1-\sin^2(x)}\\\\\Longrightarrow \int[(1-\sin^2(x)})\cos(x)]dx\\\\\Longrightarrow \int \cos(x)dx-\int (\sin^2(x)\cos(x))dx\\\\\Longrightarrow \sin(x)-\int (\sin^2(x)\cos(x))dx\\\\\text{Let} \ u=\sin(x) \rightarrow du=cos(x)dx\\\\\Longrightarrow \sin(x)-\int u^2du\\\\\Longrightarrow \sin(x)-\frac{1}{3} u^3\)\
\(\Longrightarrow \boxed{u_2=\sin(x)-\frac{1}{3} \sin^3(x)}\)
(5) - Generate the particular solution
\(\text{Particular solution} \rightarrow y_p=u_1y_1+u_2y_2\)
\(\Longrightarrow y_p=(\frac{1}{3}\cos(x))(\cos(x))+(\sin(x)-\frac{1}{3} \sin^3(x))(\sin(x))\\\\ \Longrightarrow y_p=\frac{1}{3}\cos^4(x)+\sin^2(x)-\frac{1}{3}\sin^4(x)\\\\\Longrightarrow \boxed{y_p=\sin^2(x)-\frac{1}{3}\sin^4(x)+\frac{1}{3}\cos^4(x)}\)
(6) - Form the general solution
\(\text{General solution} \rightarrow y_{gen.}=y_h+y_p\)
\(\boxed{\boxed{y=c_1\cos(x)+c_2\+\sin(x)+\sin^2(x)-\frac{1}{3}\sin^4(x)+\frac{1}{3}\cos^4(x)}}}\)
Thus, the solution to the given DE is found where c_1 and c_2 are arbitrary constants that can be solved for given an initial condition. You can simplify the solution more if need be.
AA similarity theorem

Answers
The prove that has the statements is given in the image attached.
What is the prove?The given table presents a step-by-step explanation of the proof that ΔPQR and ΔSTU are similar triangles. The proof uses the definition of similar polygons, the congruence and similarity postulates, and the properties of equality.
The first two statements state that ΔPQR and ΔSTU are given and that ∠P ≅ ∠S, ∠Q ≅ ∠T, ∠R ≅ ∠U, respectively. These are given as part of the problem.
The third statement asserts that ΔPQR is similar to ΔSTU. This follows from the fact that the corresponding angles of the two triangles are congruent, which is stated in the second statement. This is one of the criteria for the similarity of two triangles, known as the Angle-Angle (AA) Similarity Theorem.
Therefore, the fourth statement defines the concept of similar polygons, which are polygons that have the same shape but may differ in size.
Read more about SSS Similarity Theorem here:
https://brainly.com/question/4163594
#SPJ1
See text below
SSS Similarity Theorem
If the corresponding sides of two triangles are in proportion, then the two
triangles are similar.
PQ/ST ≅ QR/TU ≅ PR SU
Given:
Prove: Δ PQR ~ ΔSTU
STATEMENT
1
2.
3.
4.
5.
6.
7.
8.
6
9.
10.
11.
12.
13.
14.
REASON
1. By construction
2. Corresponding angles
are congruent
3. -------- Theorem Similarity
4. Definition of Similar Polygons
5. Given
6. By construction
7. Substitution
8. Transitive Property of Equality
9. Multiplication Property of Equality
10. SSS Triangle
Congruence Postulate
11. Definition of Congruent Triangles
12) Substitution
13. Definition of Similar Polygons
14. Transitivity


How do I solve (3.4) (6.7) using standard algorithm?
Answers
To solve the equation (3.4)(6.7) using the standard algorithm, first multiply 3.4 and 6.7. Then, the result is 22.78.
How to solve for the standard algorithm?The standard algorithm for multiplication is a step-by-step process that involves breaking down the numbers being multiplied into simpler parts, and then multiplying those parts together.
First, you would need to multiply the ones place of the first number (4) by the ones place of the second number (7), which would give you 28.
Next, you would need to multiply the ones place of the first number (4) by the tens place of the second number (6), which would give you 24.
Then, you would add the two products from steps 1 and 2 to get the result: 28 + 24 = 52.
Alternatively, you can use the distributive property of multiplication to simplify the problem.
(3.4)(6.7) = 3.46 + 3.40.7 = 22.8
Read more about standard algorithm here:
https://brainly.com/question/25232442
#SPJ1
the half-life of radium-226 is 1600 years. suppose we have a 27-mg sample. (a) how much of the sample will remain after 4500 years? (round your answer to one decimal place.) mg (b) after how many years will only 15 mg of the sample remain? (round your answer to one decimal place.) yr
Answers
(a) After 4500 years, the sample will remain 3.9 mg.
(b) The sample will remain 15 mg after 1369 years.
The result is obtained by using the exponential decay equation.
What is the exponential decay equation?The exponential decay equation can be used to calculate radioactive decay for the activity, the nuclei, and also the mass. The exponential decay equation for the mass is
\(m = m_{o} e^{-\lambda t}\)
Where
m = the initial massm₀ = the remaining massλ = decay constant (0.693/T½)T½ = half-lifet = decay timeThe half-life of radium-226 is 1600 years and the mass of a sample is 27 mg.
(a) What is the remaining mass after 4500 years?
(b) What is the decay time if the remaining mass is 15 mg?
First, let's calculate the decay constant.
λ = 0.693/T½
λ = 0.693/1600
λ = 0,000433
After 4500 years, the remaining mass is
\(m = m_{o} e^{-\lambda t}\)
\(m = 27 e^{-0.000433 \times 4500}\)
m = 27 × 0.142
m = 3.8 mg
If the remaining mass is 15 mg, the decay time is
\(m = m_{o} e^{-\lambda t}\)
\(15 = 27 e^{-0.000433 t}\)
\(ln \frac{15}{27} = ln (e^{-0.000433 t})\)
\(ln \frac{15}{27} = -0.000433 t\)
-0.588 = - 0.000433t
t = 1357.9 years
Hence,
(a) After 4500 years, the sample will remain 3.9 mg.
(b) The sample will remain 15 mg after 1369 years.
Learn more about radioactive decay here:
brainly.com/question/9796067
#SPJ4
Enter an equation in point-slope form for the line.
Slope is 1 and (−7, −1) is on the line.
The equation of the line in point slope form is: ________
Answers
9 is the y intercept
each score in a set of data is multiplied by 5, and then 7 is added to the result. if the original mean is 8 and the original standard deviation is 2, what are the new mean and new standard deviation? a. μ
Answers
The new mean of the given data is 47, and the new standard deviation for the same data is 10.
When each score in a set of data is multiplied by 5 and then 7 is added to the result, the transformation can be described as follows:
New Score = (Original Score * 5) + 7
To find the new mean, we need to apply this transformation to the original mean. Since the original mean is 8, the new mean can be calculated as:
New Mean = (Original Mean * 5) + 7
= (8 * 5) + 7
= 40 + 7
= 47
Next, to find the new standard deviation, we need to consider the effect of the transformation on the original standard deviation. Since multiplying the data by a constant (5 in this case) scales the standard deviation, the new standard deviation can be calculated as:
New Standard Deviation = Original Standard Deviation * 5
= 2 * 5
= 10
Therefore, the new mean of the data is 47, and the new standard deviation is 10.
Learn more about mean here:
https://brainly.com/question/1136789
#SPJ11
Faizah is paid $11 per hour for her work at a factory. She works 9 hours a day and 24 days a month. She saves $594 a month. Express the amount she saves as a percentage of her income.
Answers
Answer:
The amount she saves is 25% of her income
Step-by-step explanation:
She is paid $11 per hour
She works 9 hours per day
and for 24 days per month
So, she works 9(24) hours per month
= 216 hours per month
Now, she is paid $11 hourly, so for 216 hours,
she will have 11(216) = $2376
Total income = $2376 per month
Saving = $594 per month
As a percentage, we divide the savings by the total income,
savings/(total income) = 594/2376 = 1/4 = 0.25
Hence we get 25%
If this trend continues, in which week will she give a 12-minute speech?
The week that Alyssa gives a 12-minute speech is week ____
What the answer
Help ASAP

Answers
Answer:
420
Step-by-step explanation:
if we add 30 to each of the length of speech, we get 420 seconds
Tablets are on sale for 15% off the original price (t), which can be expressed with the function p(t) = 0. 85t. Local taxes are an additional 8% of the discounted price (p), which can be expressed with the function c(p) = 1. 08p. Using this information, which of the following represents the final price of a tablet, with the discount and taxes applied, based on its original price? c[p(t)] = 0. 918t t[c(p)] = 0. 918t c[p(t)] = 1. 93p t[c(p)] = 1. 93p.
Answers
Taxation is done on the discounted price. The equation representing the final price of a tablet for this condition is : Option A: c[p(t)] = 0. 918t
What are composite functions?Functions which are formed by composing two or more functions in a way that one's input is another's output unless its the last and first function is called composite functions.
For given case, it is given that
Discounted price for original 't' price of a tablet is
\(p(t) = 0.85t\)
This discounted price is then passed as input to the tax calculating function as taxation is specified to be done on the discounted price and not on the original price.
The total cost calculating function is \(c(p) = 1. 08p\)
Thus, for original price t, the total cost is given as:
\(c(p(t)) = 1.08(p(t)) = 1.08 \times 0.85t = 0.918t\)
We composed the two available function to get the direct final cost from value of t.
Thus,
The equation representing the final price of a tablet for this condition is Option A: c[p(t)] = 0. 918t
Learn more about composite functions here:
https://brainly.com/question/24780056
Which numbers are solutions of x2+20=9x+2?
Choose exactly 2 awnsers.
2
3
5
6
Answers
Answer:
my answer is gonna be 2 and 5
Brett's fish tank can hold up to 10.5 gallons of water before it overflows. Brett has poured 9 gallons of water into his fish tank so far.
Let x represent how many more gallons of water Brett can pour into his fish tank. Which inequality describes the problem?
Answers
Answer:
x=1.5
Step-by-step explanation:
Find F'(x): F(x) = Sx 3 t^1/3 dt
Answers
The derivative of F(x) is \(F'(x) = x^{(1/3)\).
What is function?A relation between a collection of inputs and outputs is known as a function. A function is, to put it simply, a relationship between inputs in which each input is connected to precisely one output.
To find the derivative of the given function F(x), we will apply the fundamental theorem of calculus and differentiate the integral with respect to x.
Let's compute F'(x):
F(x) = ∫[0 to x] \(t^{(1/3)} dt\)
To differentiate the integral with respect to x, we'll use the Leibniz integral rule:
F'(x) = d/dx ∫[0 to x] \(t^{(1/3)} dt\)
According to the Leibniz integral rule, we have to apply the chain rule to the upper limit of the integral.
\(F'(x) = x^{(1/3)} d(x)/dx - 0^{(1/3)} d(0)/dx\) [applying the chain rule to the upper limit]
Since the upper limit of the integral is x, the derivative of x with respect to x is 1, and the derivative of 0 with respect to x is 0.
\(F'(x) = x^{(1/3)} (1) - 0^{(1/3)} (0)\)
\(F'(x) = x^{(1/3)\)
Therefore, the derivative of F(x) is \(F'(x) = x^{(1/3)\).
Learn more about function on:
https://brainly.com/question/7693326
#SPJ4
Six friends are selling crafts at a flea market. they each need to pay $7. 20 to pay
for the table rental. they each sell 3 items. if every item is the same price, and the
6 friends make a total profit of $25. 20, what was the sale price of each item?
Answers
To find the sale price of each item, we need to use some basic algebra. Let's call the sale price of each item "x".
First, we need to find the total cost of the table rental for all six friends. Since each friend needs to pay $7.20, the total cost of the table rental is 6 * $7.20 = $43.20.
Next, we need to find the total revenue from selling the items. Each friend sells 3 items, so the total number of items sold is 6 * 3 = 18. The total revenue is the number of items sold multiplied by the sale price, so the total revenue is 18x.
We know that the total profit is $25.20, which is the total revenue minus the total cost of the table rental. So we can set up the equation:
18x - $43.20 = $25.20
Simplifying this equation, we get:
18x = $68.40
Dividing both sides by 18, we get:
x = $3.80
Therefore, the sale price of each item is $3.80.
To know more about algebra refer here
https://brainly.com/question/24875240#
#SPJ11
The sum of the interior angles of a polygon is 9x². If x is 3 greater than the number of side of the polygon, how many sides does the polygon have?
Answers
Answer:
17
Step-by-step explanation:
This is a very neat problem -- for teachers.
Let the number of sides = y
The sum of the interior angles is 180*(y - 2)
We are told that this sum equals 9x^2
So far the equation is
(y - 2)*180 = 9x^2 Divide both sides by 9
(y - 2)*20 = x^2 Remove the brackets on the left.
20*y - 40 = x^2
We need another fact. We get that from the statement that x is three greater than the number of sides (y). Therefore y = x - 3
20*(x - 3) - 40 = x^2
20x - 60 - 40 = x^2 Combine like terms on the left
20x - 100 = x^2 Bring the left side to the right side.
0 = x^2 - 20x + 100 You have a quadratic.
a = 1
b = - 20
c = 100
When you solve the quadratic equation, you get
x = 20
Therefore the number of sides is 17.
what is the slope of the line that contains these points?
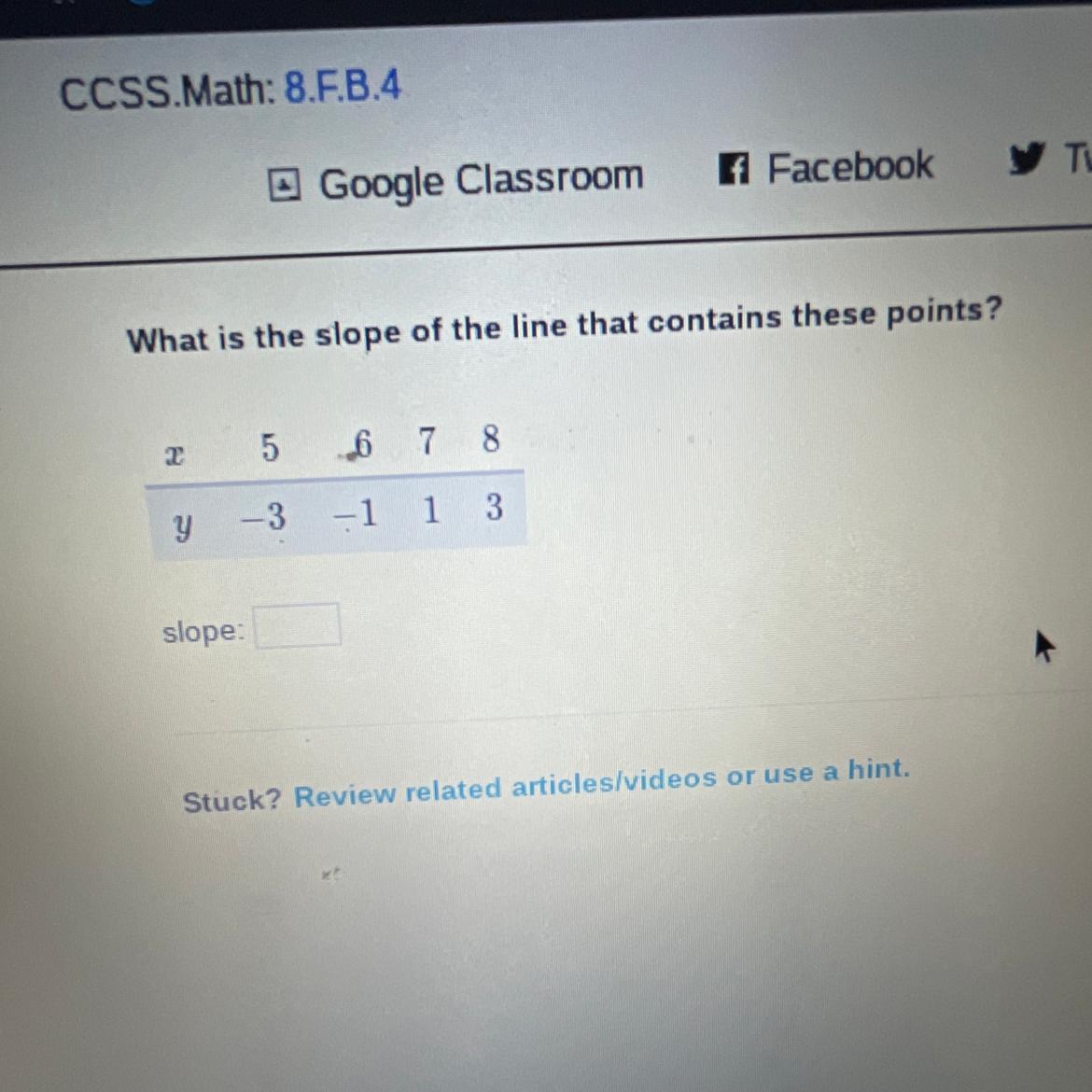
Answers
Answer:
2
Step-by-step explanation:
When finding the slope of a line, only two points are needed. Four points are listed here. I'm going to use the first one and the second one.
The slope formula is m= (y2-y1)/(x2-x1) when m=the slope, or your answer. It is used to determine the slope with two points. The numbers after the ys and xs represent which set of points to take them from, so you don't get confused.
(5, -3) and (6, -1)
First, you take the y value of the second point (y2), and you subtract the y value of the first point (y1) from it. -1-(-3)=-1+3=2
Then, take the x value of the second point (x2) and subtract the x value of the first point (x1). 6-5=1
2 (the difference of the y values) / 1 (the difference of the x values) = 2/1 = 2. m=2. Your slope is 2. This can then be plugged into a slope/intercept equation, y=mx+b, where m=slope (solved above) and b=the y intercept, hence the name, slope/intercept form.
find the distaance between the points (-5,7) and (-5,2)
Answers
Answer: The distance between these two points is 5.
Step-by-step explanation:
Yay! Love doing distance formula questions!
Okay, so first off, the distance formula goes as follows:
d = \(\sqrt(x^{2} - x^1)^2 + (y^{2}-y^1)^2\)
Basically you just plug in your coordinates to the formula.
Step 1:
\(\sqrt(-5 + 5)^{2} + (2-7)^{2}\)
Step 2: Distribute the exponent to both parenthesis to get \(\sqrt{25}\).
Step 3: Factor the number, which would result in \(\sqrt{5^2}\).
As a result of this, your answer would be 5.
Write equations for the horizontal and vertical lines passing through the point , −8−5.
Answers
Combine the like terms to create an equivalent expression:
2r+1+(−4r)+7
Answers
Answer:
-2r+8
Step-by-step explanation:
Hope this helps :)
Margo bought the following lengths of ribbon: 3/4 yd, 1/3 yd, 1/2 yrd. How much ribbon did she buy?
Answers
Answer:
she bought 19/12 lengths of ribbon or aka 1 7/12
Step-by-step explanation:
3/4 + 1/3 + 1/2 = 13/12 + 1/2
13/12 +1/2 = 19/12
19/12 simplify is 1 7/12
Margo bought \(1\frac{2}{3}\) yards of ribbon.
What is a fraction ?A fraction represents how much part of total quantity is present.Fractions are of two types proper fraction and improper fraction.
According to the question given Margo bought some ribbons of length 3/4 yd, 1/3 yd and 1/2 yd.
To find the total ribbon she bought in yards we have to take the sum of all the fractions.
∴ (3/4) + (1/3) + (1/2) yards.
Now to sum these fractions we have to take LCM of the denominators which is 12.
So, { (3×3) + (1×4) + (1×6) }/12.
= (9 + 4 + 6)/12.
= 19/12 or 1 whole 2/3 yards of ribbon.
learn more about fractions here :
https://brainly.com/question/8482939
#SPJ2