Jonah has 12$ to spend on lunch he decides to buy 1 sandwich, 1 beverage, and some bags of chips.
What is the greatest number of bags of chips Jonah can buy?

Answers
Answer:
He can buy up to 3 bags of chips
Step-by-step explanation:
Depending what sandwich and drink he gets is what this problem is about. I just took the cheapest sandwich and cheapest drink and took those from his money leaving $4.88 left. Since a bad of chips costs 1.50 I took that and added them to see how many he could buy or whatever and I got 3 bags of chips leaving him with 0.38 cents to spare
Related Questions
The actual tracking weight of a stereo cartridge that is set to track at 3 g on a particular changer can be regarded as a continuous rv X with the following pdf. Sketch the graph of f(x). Find the value of k. What is the probability that the actual tracking weight is greater than the prescribed weight? What is the probability that the actual weight is within 0.5 g of the prescribed weight? What is the probability that the actual weight differs from the prescribed weight by more than 0.55 g?
Answers
The sketch of graph of f(x) is downward-facing parabola. The value of K is 1/6. The probability that the actual tracking weight is greater than the prescribed weight is 2/9. The probability that the actual weight is within of the .25g prescribed weight is 1/2. The probability that the actual weight differs from the prescribed weight by more than 0.5 g is approximately 0.3334.
To sketch the graph of f(x), we first note that the function is defined only on the interval [2, 4], and it is zero everywhere else. On this interval, the function is a downward-facing parabola centered at x = 3. We can plot the graph.
To find the value of k, we need to use the fact that the total area under the curve of f(x) must be equal to 1, since f(x) is a probability density function. Therefore, we can integrate f(x) over the interval [2, 4] and set the result equal to 1:
1 = ∫[2,4] k(1 - (x-3)^2) dx
= k[x - (x-3)^3/3] evaluated from 2 to 4
= k[(4 - (4-3)^3/3) - (2 - (2-3)^3/3)]
= k(4 - 8/3 + 2 + 8/3)
= k(6)
Thus, k = 1/6.
To find the probability that the actual tracking weight is greater than the prescribed weight of 3g, we need to integrate f(x) over the interval [3, 4]:
P(X > 3) = ∫[3,4] f(x) dx
= ∫[3,4] 1/6(1 - (x-3)^2) dx
= 1/6[x - (x-3)^3/3] evaluated from 3 to 4
= 1/6[(4 - (4-3)^3/3) - (3 - (3-3)^3/3)]
= 1/6(4 - 8/3)
= 2/9
Therefore, the probability that the actual tracking weight is greater than the prescribed weight.
The given pdf is:
f(x) = k(1 - (x-3)^2) 2 <= x <= 4
0 otherwise
To find the value of k, we need to integrate the pdf over its support, which is from 2 to 4, and set the result equal to 1:
1 = ∫₂⁴ k(1 - (x-3)^2) dx
= k ∫₂⁴ (1 - (x-3)^2) dx
= k [x - (x-3)^3/3] ₂⁴
= k [4 - (4-3)^3/3 - 2 + (2-3)^3/3]
= k [8/3 - 2/3]
= 2k
Therefore, k = 1/2.
To find the probability that the actual weight differs from the prescribed weight by more than 0.5 g, we need to calculate the probability of the event { |X - 3| > 0.5 }. This event represents the set of all values of X that are more than 0.5 g away from the prescribed weight of 3 g.
We can calculate this probability as follows:
P(|X - 3| > 0.5) = P(X < 2.5 or X > 3.5)
= P(X < 2.5) + P(X > 3.5) (by the addition rule of probability)
Now, using the given pdf of X, we can find these probabilities as:
P(X < 2.5) = 0 (since f(x) = 0 for x < 2.0)
P(X > 3.5) = ∫(3.5 to 4) f(x) dx
= ∫(3.5 to 4) k(1-(x-3)^2) dx (using the given pdf)
= k ∫(0.5 to 1) (1-t^2) dt (where t = x-3)
= k [t - (1/3)t^3] (evaluating the integral)
= k [(4-3.5) - (1/3)((1-0.5^3)]
= k [0.1667]
Therefore, the required probability is:
P(|X - 3| > 0.5) = P(X < 2.5 or X > 3.5) = P(X > 3.5) = k [0.1667]
We need to find the value of k to calculate the probability. The pdf of X must integrate to 1 over its entire domain, so we have:
1 = ∫(2 to 4) f(x) dx
= k ∫(2 to 4) (1-(x-3)^2) dx
= k ∫(-1 to 1) u (1-u^2) du (where u = x-3)
= k [u^2/2 - u^4/4] (evaluating the integral)
= k [(1/2) - (1/4)]
= k [0.5]
Thus, k = 2.
Substituting this value of k in the expression we derived earlier, we get:
P(|X - 3| > 0.5) = P(X < 2.5 or X > 3.5) = P(X > 3.5) = k [0.1667]
= 2 [0.1667]
= 0.3334
Therefore, the probability is more than 0.5 g is approximately 0.3334.
To know more about Probability:
https://brainly.com/question/11234923
#SPJ4
_____The given question is incomplete, the complete question is given below:
The actual tracking weight of a stereo cartridge that is set to track at 3g
on a particular changer can be regarded as a continuous rv X
with pdf f(x) = k(1-(x-3)^2) 2less than equal to x less than equal to 4, f(x) = 0 otherwise
a. Sketch the graph of f(x)
.
b. Find the value of k.
.
c. What is the probability that the actual tracking weight is greater than the prescribed weight?
d. What is the probability that the actual weight is within
of the .25g prescribed weight?
e. What is the probability that the actual weight differs from the prescribed weight by more than .5g
?

(7x-49x^2)/(7x) can smeone solve this? Thank you! I hope you have a great day!
Answers
Answer:
x = 1/7
Step-by-step explanation:
\(\frac{(7x-49x^2)}{7x}\\\\\frac{7x(1-7x)}{7x} \\\\1-7x=0\\\\1=7x\\\\\)
x = 1/7
Taxi A charges $0.20 per mile
Answers
Answer:
and what about the other Taxi's?
Step-by-step explanation:
If an artile bought for US $ 1 is sold for sterling £1, what is the gain percent? (Given, \$ 1 = Rs. 105.52, £1= Rs. 155.63)
Answers
Answer:
47.49%
Step-by-step explanation:
profit / selling price ×100% = gain percent
profit =selling price - cost price
therefore profit = 155.63 - 105.52 = 50.11
50.11/105.52 ×100% = gain percent
47.49% = gain percent
In kite ABCD, mZBAE = 28º and mZBCE = 58°. Find mZABE.
B
E
А
С
D
mLABE =

Answers
Answer:
m∠ABE = 62°
Step-by-step explanation:
Since, the given quadrilateral is a kite, diagonals will intersect at 90°.
Therefore, m∠AEB = m∠CEB = 90°
m∠BAE = 28° [Given]
m∠BCE = 58° [Given]
From ΔABE,
m∠BAE + m∠BEA + m∠ABE = 180°
28° + 90° + m∠ABE = 180°
m∠ABE = 180° - 118°
= 62°
Therefore, measure of angle ABE = 62°.
For each of the following operations, show the value of R0 in base-10 signed representation (e.g., If R0 = -64, then R0 ASR #1 = -32). In the questions below, it using logical operations on signed numbers is noted as abnormal. For these questions, assume that the register R0 contains a signed 32-bit integer (e.g., int32_t) with a value of -4 (0xFFFFFFFC) R0 ASR
Answers
R0 ROR #1 = 2147483645. LSR and ROR, being logical operations, may lead to different interpretations and should be used with caution when dealing with signed numbers.
To provide the value of R0 in base-10 signed representation after each operation, we'll assume that the initial value of R0 is -4 (0xFFFFFFFC). Let's calculate the values of R0 for the given operations:
a) R0 ASR #1:
ASR (Arithmetic Shift Right) performs a right shift operation on the binary representation of a signed number, preserving the sign bit. In this case, the shift is performed by 1 bit.
Starting with R0 = -4 (0xFFFFFFFC):
- The binary representation of -4 is 11111111111111111111111111111100.
- Performing an arithmetic right shift by 1 bit, we shift all bits to the right and preserve the sign bit.
- After the right shift, the binary representation becomes 11111111111111111111111111111110.
- Converting the binary representation back to base-10 signed representation, we have -2.
Therefore, R0 ASR #1 = -2.
b) R0 LSR #1:
LSR (Logical Shift Right) performs a right shift operation on the binary representation of a signed number, shifting all bits to the right and filling the leftmost bit with zero.
Starting with R0 = -4 (0xFFFFFFFC):
- The binary representation of -4 is 11111111111111111111111111111100.
- Performing a logical right shift by 1 bit, we shift all bits to the right and fill the leftmost bit with zero.
- After the right shift, the binary representation becomes 01111111111111111111111111111110.
- Converting the binary representation back to base-10 signed representation, we have 2147483646.
Therefore, R0 LSR #1 = 2147483646.
c) R0 ROR #1:
ROR (Rotate Right) performs a right rotation operation on the binary representation of a signed number. The rightmost bit is shifted to the leftmost position.
Starting with R0 = -4 (0xFFFFFFFC):
- The binary representation of -4 is 11111111111111111111111111111100.
- Performing a right rotation by 1 bit, we rotate all bits to the right and move the rightmost bit to the leftmost position.
- After the right rotation, the binary representation becomes 01111111111111111111111111111101.
- Converting the binary representation back to base-10 signed representation, we have 2147483645.
Therefore, R0 ROR #1 = 2147483645.
It's important to note that performing logical operations on signed numbers can yield unexpected results. In the given examples, ASR is the appropriate operation for maintaining the sign bit and preserving the signed representation. LSR and ROR, being logical operations, may lead to different interpretations and should be used with caution when dealing with signed numbers.
Learn more about logical operations here
https://brainly.com/question/14861063
#SPJ11
I don’t understand this question! Please help me find the answer they are compound shapes

Answers
The area of the shaded region in this problem is given as follows:
995.44 cm².
How to calculate the area of a circle?The area of a circle of radius r is given by the multiplication of π and the radius squared, as follows:
A = πr²
The radius of a circle represents the distance between the center of the circle and a point on the circumference of the circle, hence it's measure is given as follows:
r = 21 cm.
Then the area of the entire circle is given as follows:
A = π x 21²
A = 1385.44 cm².
The right triangle has two sides of length 39 cm and 20 cm, hence it's area is given as follows:
A = 0.5 x 39 x 10
A = 390 cm².
Then the area of the shaded region is given as follows:
1385.44 - 390 = 995.44 cm².
More can be learned about the area of a circle at https://brainly.com/question/15673093
#SPJ1
If
θ
θ
is an acute angle of a right triangle and
tan θ=
3
5
tan θ=35
, what is the value of
cosθ
cosθ
?
Answers
Given:
In a right angle triangle θ is an acute angle and \(\tan\theta =\dfrac{3}{5}\).
To find:
The value of \(\cos \theta\).
Solution:
In a right angle triangle,
\(\tan \theta=\dfrac{Perpendicular}{Base}\)
We have,
\(\tan\theta =\dfrac{3}{5}\)
It means the ratio of perpendicular to base is 3:5. Let 3x be the perpendicular and 5x be the base.
By using Pythagoras theorem,
\(Hypotenuse=\sqrt{Perpendicular^2+base^2}\)
\(Hypotenuse=\sqrt{(3x)^2+(5x)^2}\)
\(Hypotenuse=\sqrt{9x^2+25x^2}\)
\(Hypotenuse=\sqrt{34x^2}\)
\(Hypotenuse=x\sqrt{34}\)
In a right angle triangle,
\(\cos \theta=\dfrac{Base}{Hypotenuse}\)
\(\cos \theta=\dfrac{5x}{x\sqrt{34}}\)
\(\cos \theta=\dfrac{5}{\sqrt{34}}\)
Therefore, the value of \(\cos \theta\) is \(\dfrac{5}{\sqrt{34}}\).
Which graph shows the solution to y > x – 8?

Answers
Answer: Your answer is B.
Step-by-step explanation: y > x means y is bigger than x and also -8 means that you subtract 8 from x so its B
Factor by grouping.
64p2 – 48p – 27
(8p – 9)(8p – 3)
(8p – 9)(8p + 3)
(8p + 9)(8p + 3)
(8p + 9)(8p – 3)
Answers
Answer:
B
Step-by-step explanation:
hope this helps with the work
In proof by contradiction, you prove a statement by assuming its negation and obtaining a contradiction. true or false
Answers
The Statement "In proof by contradiction, you prove a statement by assuming its negation and obtaining a contradiction" is True.
In a proof by contradiction, you prove a statement by assuming its negation and obtaining a contradiction. This method is often used to establish the truth of a mathematical proposition or statement.
To begin a proof by contradiction, you assume the opposite of what you want to prove, known as the negation of the statement. Then, you proceed with logical deductions and mathematical reasoning to derive a contradiction. If you reach a point where you obtain a statement or conclusion that is clearly false or contradicts a known fact or assumption, then you can conclude that the original statement must be true.
The idea behind proof by contradiction is that if assuming the negation leads to a contradiction, then the original statement cannot be false. By negating the statement and showing that it leads to an impossible or contradictory situation, you establish the truth of the original statement.
Proof by contradiction is a powerful technique used in many areas of mathematics and logic to establish the validity of various theorems and propositions.
To know more about contradiction, refer here:
https://brainly.com/question/28568952#
#SPJ11
A triangle has an area of 30cm². The base and height are scaled by a factor of 3. What is the area of the resulting triangle? _cm²
Answers
Answer:
A triangle has an area of 30cm². The base and height are scaled by a factor of 3. What is the area of the resulting triangle? _cmA triangle has an area of 30cm². The base and height are scaled by a factor of 3. What is the area of the resulting triangle? _cm²²
A triangle in which one angle is greater than 90 degree is called______.
Answers
An obtuse angle is some angle x such that 90 < x < 180.
An obtuse triangle has one obtuse angle. The other two angles are acute (they are less than 90 degrees).
An obtuse triangle is a type of triangle that has one angle greater than 90 degrees.
An obtuse triangle is a type of triangle that has one angle greater than 90 degrees. In other words, one of the angles in an obtuse triangle is 'blunt' or 'dull' and measures more than 90 degrees. The other two angles in an obtuse triangle are acute angles, which means they are less than 90 degrees.
The sum of the measures of the three angles in any triangle is always 180 degrees. In an obtuse triangle, the sum of the measures of the three angles is greater than 180 degrees because one of the angles is greater than 90 degrees.
For example, if we have an obtuse triangle with angles measuring 100 degrees, 40 degrees, and 40 degrees, the sum of the angles would be 180 degrees, with one angle greater than 90 degrees.
Learn more:About obtuse triangle here:
https://brainly.com/question/2617159
#SPJ11
Which equation can be used to find the value of x?

Answers
Answer:
\(x=5.24\tan 41^{\circ}\)
Step-by-step explanation:
\(\tan 41^{\circ}=\frac{x}{5.24} \\ \\ x=5.24\tan 41^{\circ}\)
PLEASEEE HELP MEEEEE EASY 10 POINTSSS

Answers
Answer:
y = -3x + 3
Hope this helps, thank you !!

An equation is shown below: 4(x - 3) - 5(x + 1) = 3
Which statement shows a correct next step in solving the equation?

Answers
I think its the last one
Kiran ate breakfast in a café. His total check was $15.
a. What’s a 20% tip?
b. How much money did Kiran spend altogether for breakfast?
Answers
Answer:
A 20 percent tip is basically multiplying the price by 0.2
Percent means out of a hundred.
20/100 is 0.2
We have to find 0.2 of 15.
We can multiply 15 by 0.2 to find 20 percent of 15 and you would get 3.
20 percent of 15 is 3 dollars thats your answer to A
Now the total price would just be the percentage you found in A and add it to the total breakfast.
3 + 15 = 18
Kieran spend 18 dollars for brekfast.
Solve for x. (round to the nearest tenth)
This is for my high school final exam so please answer fast

Answers
Step-by-step explanation:
(sin90)/20= sin67)/x
x= 18
Write the slope-intercept form of the equation of each line.3) 6x - 8y = 404) -10 + 3x = -5y
Answers
Given data:
The expression for the equation of the line is 6x-8y=40.
The given equation can be written as,
6x-8y=40
8y=6x-40
y=6x/8-40/8
=3x/4-5
Thus, the slope intercept form is y=3x/4-5.
Please Help! 60 points for a rapid reply- please look at the question below= The Figure of circle A shown has a diameter of PR which intersects with QS at point B and the measurements shown, Calculate the following measures-


Answers
The measures in the circle given in the image above are calculated as:
1. m<PSQ = 130°; 2. m<AQS = 30°; 3. m(QR) = 100°; 4. m(PS) = 110°; 5. (RS) = 70°.
How to Find the Measures in the Circle?In order to find the measures in the circle shown, recall that according to the inscribed angle theorem, the measure of intercepted arc is equal to the central angle, but is twice the measure of the inscribed angle.
1. m<PSQ = m<PAQ
Substitute:
m<PSQ = 130°
2. Find m<PBQ:
m<PBQ = 1/2(m(PQ) + m(RS)) [based on the angles of intersecting chords theorem]
Substitute:
m<PBQ = 1/2(130 + 2(35))
m<PBQ = 100°
m<AQS = 180 - [m<BAQ + m<PBQ]
Substitute:
m<AQS = 180 - [(180 - 130) + 100]
m<AQS = 30°
3. m(QR) = m<QAR
Substitute:
m(QR) = 100°
4. m(PS) = 180 - m(RS)
Substitute:
m(PS) = 180 - 2(35)
m(PS) = 110°
5. m(RS) = 2(35)
m(RS) = 70°
Learn more about Measures in a Circle on:
https://brainly.com/question/27111486
#SPJ1
What is 1131 divided by 29?
Answers
Answer:
39
Step-by-step explanation:
used a calculator
Explaination:
A man is five times as old as his son. Four years ago the man was thirteen times as old as his son.
Find their present ages.
Answers
Answer:
Age of son = 6 years
Age of man = 5×6 = 30 years
Step-by-step explanation:
GIVEN :-
A man is 5 times as old as his son. (In Present)4 years ago , the man was 13 times as old as his sonTO FIND :-
The present ages of the man & his son.SOLUTION :-
Let the present age of son be 'x'.
⇒ Present age of man = 5x
4 years ago ,
Age of son = (Present age of son) - 4 = x - 4
Age of man = (Present age of man) - 4 = 5x - 4
The man was thirteen times as old as his son. So,
\(=> 5x - 4 = 13(x - 4)\)
Now , solve the equation.
Open the brackets in R.H.S.\(=> 5x - 4 = 13x - 52\)
Take 5x to R.H.S. and -52 to L.H.S. Also , take care of their signs because they are getting displaced from L.H.S. to R.H.S. or vice-versa.\(=> 13x - 5x = 52 - 4\)
\(=> 8x = 48\)
Divide both the sides by 8\(=> \frac{8x}{8} = \frac{48}{8}\)
\(=> x = 6\)
CONCLUSION :-
Age of son = 6 years
Age of man = 5×6 = 30 years
3. The system of equations for two liquid surge tanks in series is
A₁ dh'₁/dt = q'ᵢ - 1/R₁ h'₁, q'₁ = 1/R₁ h'₁
A₂ dh'₂/dt = 1/R₁ h'₁ - 1/R₂ h'₂ q'₂ = 1/R₂ h'₂
Using state-space notation, determine the matrices A,B,C, and D assuming that the level deviations are the state variables: h'₁ and h'₂. The input variable is q'ᵢ , and the output variable is the flow rate deviation, q'₂.
Answers
The surge tank is a vital component of a system in which the flow rate fluctuates significantly. The flow rate entering the tank varies significantly, causing the fluid level in the tank to fluctuate as a result of the compressibility of the liquid. The surge tank is utilized to reduce pressure variations generated by a rapidly fluctspace uating pump flow rate. To determine the matrices A,B,C, and D using state-space notation, here are the steps:State representation is given by:dx/dt = Ax + Bu; y = Cx + DuWhere: x represents the state variablesA represents the state matrixB represents the input matrixC represents the output matrixD represents the direct transmission matrixThe equation can be written asA = [ -1/R₁ 0; 1/R₁ -1/R₂]B = [1/A₁; 0]C = [0 1/R₂]D = 0Thus, the matrices A,B,C and D assuming that the level deviations are the state variables: h'₁ and h'₂. The input variable is q'ᵢ, and the output variable is the flow rate deviation, q'₂ are given by A = [ -1/R₁ 0; 1/R₁ -1/R₂]B = [1/A₁; 0]C = [0 1/R₂]D = 0.Hence, the required matrices are A = [ -1/R₁ 0; 1/R₁ -1/R₂], B = [1/A₁; 0], C = [0 1/R₂], and D = 0 using state-space notation for the given system of equations for two liquid surge tanks.
surge tank: https://brainly.com/question/14143728
#SPJ11
A company created a census to see the impact of pollution in its state. The company attempted to interview every resident of the state. The people it interviewed are an example of a _____.
A.) survey
B.) population
C.) sample
D.) census
Answers
Exclamation:
6²- (8 x 3)+2² (7 x 3)
Answers
BODMAS is an acronym to help children remember the order of mathematical operations – the correct order in which to solve maths problems. Bodmas stands for
B-Brackets,
O-Orders (powers/indices or roots),
D-Division,
M-Multiplication,
A-Addition,
S-Subtraction.
This is the order.
Answer is 96

Answer:96
Step-by-step explanation:36-8(-3)=9
Please solve this giving 150 points plus the crown
I have been looking everywhere for this and still can't find it so please help me please odnt spam/scam me because it took me a while to gt the points.

Answers
Answer:
money saved = 1.5 x time
Step-by-step explanation:
Find the gradient with rise over run
3/2 = 1.5
Answer:um i think money saved = 1.5 x time
im not 100% sure but i think it is right
Step-by-step explanation:
Solve for x.
X
A
=
2
C
1
B
1
E
X
D
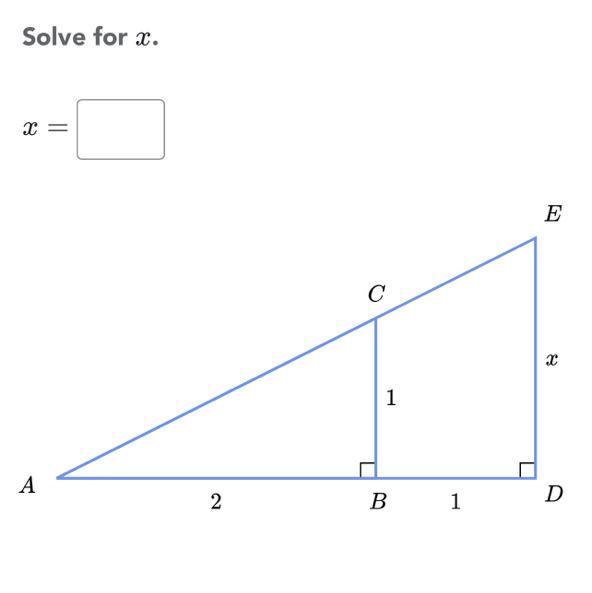
Answers
Step-by-step explanation:
ABC and ADE are similar triangles.
that means they have the same angles, and there is one scaling factor for all sides from one triangle to the other.
so, we see that AB = 2, AD = 2+1 = 3
the scaling factor f from AB to AD is then
AB × f = AD
2 × f = 3
f = 3/2
the same scaling factor now applies between BC and DE (= x).
BC × f = x
1 × 3/2 = x
x = 3/2 = 1.5
What is the probability of not drawing a queen from a standard deck of 52 cards?
Answers
The probability of not drawing a queen from a standard deck of 52 cards is 12/13
How to determine the probability of not drawing a queen from a standard deck of 52 cards?In a standard deck of 52 cards, we have
Total number of cards = 52
Queen cards = 4
The probability of not drawing a queen from a standard deck of 52 cards is calculated as
P = 1 - P(Queen)
Where
P(Queen) = Queen cards/Total number of cards
So, we have
P(Queen) = 4/52
Substitute P(Queen) = 4/52 in the equation P = 1 - P(Queen)
This gives
P = 1 - 4/52
Evaluate the difference
P = 48/52
Simplify
P = 12/13
Hence, the probability of not drawing a queen from a standard deck of 52 cards is 12/13
Read more about probability at
https://brainly.com/question/24756209
#SPJ1
Answer:
12/13
Step-by-step explanation:
Got it right on the test.
A growing number of thieves are using keylogging programs to steal passwords and other personal information from Internet
users. The number of keylogging programs reported grew approximately exponentially from 0.4 thousand programs in 2000 to
13.0 thousand programs in 2005. Predict the number of keylogging programs that will be reported in 2014.
There will be thousand keylogging programs in 2014.
(Round to the nearest integer as needed)
Answers
It is predicted that there will be approximately 122 thousand keylogging programs reported in 2014.
To predict the number of keylogging programs that will be reported in 2014, we can use the given information about the growth rate of keylogging programs from 2000 to 2005.
The data indicates that the number of keylogging programs grew approximately exponentially from 0.4 thousand programs in 2000 to 13.0 thousand programs in 2005.
To estimate the number of keylogging programs in 2014, we can assume that the exponential growth trend continued during the period from 2005 to 2014.
We can use the exponential growth formula:
N(t) = \(N0 \times e^{(kt)\)
Where:
N(t) represents the number of keylogging programs at time t
N0 is the initial number of keylogging programs (in 2000)
k is the growth rate constant
t is the time elapsed (in years)
To find the growth rate constant (k), we can use the data given for the years 2000 and 2005:
N(2005) = N0 × \(e^{(k \times 5)\)
13.0 = 0.4 × \(e^{(k \times 5)\)
Dividing both sides by 0.4:
\(e^{(k \times 5)\) = 32.5
Taking the natural logarithm (ln) of both sides:
k × 5 = ln(32.5)
k = ln(32.5) / 5
≈ 0.4082
Now, we can use this growth rate constant to predict the number of keylogging programs in 2014:
N(2014) = N0 × \(e^{(k \times 14)\)
N(2014) = 0.4 × \(e^{(0.4082 14)\)
Using a calculator, we can calculate:
N(2014) ≈ \(0.4 \times e^{5.715\)
≈ 0.4 × 305.28
≈ 122.112
Rounding to the nearest integer:
N(2014) ≈ 122
For similar questions on keylogging programs
https://brainly.com/question/28610948
#SPJ8
if shoulders bought twice as many footballs as basketballs and the footballs cost $60 and the basketballs cost $30 and he spends $450, then how many footballs did he purchase?
Answers
Using equations, we can find that he purchased 6 footballs.
What are equations?An equation is a mathematical statement that contains the symbol "equal to" between two expressions with identical values. As in 3x + 5 = 15, for example.
Here in the question,
Let the number of footballs purchased be f.
Let the number of basketballs purchased be b.
Cost of each football = $60.
Cost of each basketball = $30.
Total amount spent = $450
Now,
60f + 30b = 450
Given,
2b = f
⇒ b = f/2
Putting the value of b in the equation,
60f + 30(/2f) = 450
⇒ 60f + 15f = 450
⇒ 75f = 450
⇒ f = 6
Therefore, he purchased 6 footballs.
To know more about equations, visit:
https://brainly.com/question/29657983
#SPJ1