John went to the store and bought 4 pencils
and 10 binders and spent $64. Carmen went
to the same store and bought 7 pencils and 4
binders and spent $31. If Lisa wants to buy
pencils and binders from the same store,
how much should they tell her each item
costs?
Answers
X= pencils and Y= binders
4x + 10y = 64
7x + 4y= 31
Pencils are $1 each and binders are $6 each.
Related Questions
NRTW is a parallelogram whose diagonals intersect at point B. Some measurements are given. NW = 6x − 10. 5 BW = 6x − 7. 7 TB = 2x + 11. 6 TW = 6x + 16 WR = 221 What equation can be used to determine the value of x ?
Answers
Therefore , the solution of the given problem of parallelograms comes out to be x = -1.25.
What is parallelograms?
In Euclidean mathematics, a parallelogram is actually a simple hexagon with two distinct groups and equal distances. A specific kind of quadrilateral called a parallelogram is formed when both sets of sides equally share a horizontal path. Parallelograms come in four different varieties, three of which are mutually exclusive.
Here,
We know that NRTW's opposing sides are parallel and congruent because it is a parallelogram. As a result, we have:
=> NW = TR = 6x - 10.5
and
=> TW = RN = 6x plus 16
Additionally, since we are aware that a parallelogram's diagonals are bisectional, we have:
=> TB = BW + 5.7
=> TB = 6x - 7.7
Let's now construct an equation using the fact that the diagonals intersect at position B:
=>TB + BW = TW + RN
Inputting the numbers provided yields:
=> 6x - 7.7 + 5.7 = 6x + 16 + 6x - 10.5
When we simplify and find x, we obtain:
=> 6x - 2 = 12x + 5.5
=> -6x = 7.5
=> x = -1.25
However, the problem does not make logic given that this value of x is negative.
To know more about parallelograms visit:
https://brainly.com/question/29147156
#SPJ1
which of the following statements is true based on the function f(x), below
Answers
please help as quick as you can
Answers
Answer:
A≈188.5
Step-by-step explanation:
A=2πrh+2πr^2=2·π·3·7+2·π·3^2≈188.49556
A WSU student was interested in analyzing the time it takes the CUE Bus to complete her commute from the Vienna Metro to WSU. She collected data for 600 trips she took during her tenure at WSU. (c) Relative Frequency Normal: Mean 33.1, SD=1.835 Relative Frequency 02 0.15 0.05 0.05 01 3035 Time 2015 Time 1. (c)Using the histogram, determine the proportion of trips that took 32 minutes or less. 164 individual times are highlighted for trips that took 32 minutes or less. 2. (d) it is reasonable to use the normal probability model in this case? provide a reason why 600 18 Column Mean Std. dev. Time 33.1 4. assume that the distribution of trip times in the population is normal with the mean and standard deviation found in part (f) Note: you are using the normal distribution for the next three calculations. 5. Calculate the probability that a randomly selected trip time takes 32 minutes or less. Draw a picture with the mean labeled, shade the area representing the desired probability standardize, and use the Standard NormalTable to obtain this probability. Write one sentence to explain what the probability means in context of the question. 6. Compare this probability to the proportion you calculated in part 1 (c). Label each probability as a theoretical or an empirical probability in your comparison. 7. The student declared that the top 4% of times made her late to class. Find the minimum time where this time or higher would place the trip time in the top 4% of all times. Draw a picture or two), shade the area, and use the standard normal table to solve this problem, write one sentence to explain what the probability means in context of the question.
Answers
The probability that a randomly selected trip from Vienna Metro to WSU takes between 31 and 34 minutes is approximately 0.4857.
The probability that a randomly selected trip from Vienna Metro to WSU takes between 31 and 34 minutes can be calculated as follows:
Then, we want to find:
P(31 ≤ X ≤ 34)
We can standardize the random variable using the z-score formula:
z = (X - μ) / σ
z1 = (31 - 33.1) / 1.835 ≈ -1.14
z2 = (34 - 33.1) / 1.835 ≈ 0.49
Using a standard normal distribution table or calculator, we can find the probabilities for the corresponding z-scores:
P(-1.14 ≤ Z ≤ 0.49) ≈ 0.6602 - 0.1745 ≈ 0.4857
To know more about probability, here
brainly.com/question/30034780
#SPJ4
--The complete Question is, Assuming that the collected data follows a normal distribution with a mean of 33.1 and a standard deviation of 1.835, the question could be: What is the probability that a randomly selected trip from Vienna Metro to WSU takes between 31 and 34 minutes? --
(a)A line through (2,1) meets the curve x²-2x-y=3at A (-2,5)and at B. Find the coordinates of B
(b) A(3,1) lies on the curve (x-1)(y+1)=4. A line through A perpendicular to x+2y=7 meets the curve again at B. Find the coordinates of B.
Answers
The slope of the line passing through these two points is:
m = (y2 - y1) / (x2 - x1) = (1 - 5) / (2 - (-2)) = -4/4 = -1
Using the point-slope form of the equation of a line, the equation of the line passing through A and (2,1) is:
y - 5 = -1(x + 2)
y - 5 = -x - 2
y = -x + 3
To find the coordinates of point B, we need to solve the system of equations formed by the equation of the line and the equation of the curve:
x² - 2x - y = 3
y = -x + 3
Substituting the second equation into the first, we get:
x² - 2x - (-x + 3) = 3
x² - x - 6 = 0
Solving for x using the quadratic formula, we get:
x = (1 ± √(1 + 24)) / 2 = 3 or -2
When x = 3, y = -x + 3 = 0, which means that point B is (3,0).
When x = -2, y = -x + 3 = 5, which means that point B is (-2,5).
Therefore, the coordinates of point B are (3,0) and (-2,5).
(b) We know that point A (3,1) lies on the curve (x-1)(y+1)=4.
Substituting x=3 and y=1 into this equation, we get:
(3-1)(1+1) = 4
4 = 4
Therefore, point A satisfies the equation of the curve.
We need to find the equation of the line passing through point A that is perpendicular to the line x+2y=7.
The slope of the line x+2y=7 is:
m = -1/2
The slope of a line perpendicular to this line is the negative reciprocal, which is:
m' = 2
Using the point-slope form of the equation of a line, the equation of the line passing through A(3,1) with slope 2 is:
y - 1 = 2(x - 3)
y - 1 = 2x - 6
y = 2x - 5
To find the coordinates of point B, we need to solve the system of equations formed by the equation of the line and the equation of the curve:
(x-1)(y+1) = 4
y = 2x - 5
Substituting the second equation into the first, we get:
(x-1)(2x-4) = 4
2x³ - 6x² + 4x - 5 = 0
We can use numerical methods to solve this cubic equation to get the value of x, and then substitute it back into the equation y = 2x - 5 to get the value of y. One possible solution is:
x ≈ 2.632
y ≈ -0.736
Therefore, the coordinates of point B are approximately (2.632, -0.736).
e) What fraction is equal to 50% of
1/6
?
Answers
Answer:
1/12
Step-by-step explanation:
Answer:
1/12
Step-by-step explanation:
50/100*1/6
1/12
What is the mathematical expression for modified Reynolds Analogy, also known as Chilton-Colburn analogy?
Answers
The modified Reynolds analogy, also known as the Chilton-Colburn analogy, is expressed mathematically as Nu = f * Re^m * Pr^n. It relates the convective heat transfer coefficient (h) to the skin friction coefficient (Cf) in fluid flow. This equation is widely used in heat transfer analysis and design applications involving forced convection.
The modified Reynolds analogy is a useful tool in heat transfer analysis, especially for situations involving forced convection. It provides a correlation between the heat transfer and fluid flow characteristics. The Nusselt number (Nu) represents the ratio of convective heat transfer to conductive heat transfer, while the Reynolds number (Re) characterizes the flow regime. The Prandtl number (Pr) relates the momentum diffusivity to the thermal diffusivity of the fluid.
The equation incorporates the friction factor (f) to account for the energy dissipation due to fluid flow. The values of the constants m and n depend on the flow conditions and geometry, and they are determined experimentally or by empirical correlations. The modified Reynolds analogy is widely used in engineering calculations and design of heat exchangers, cooling systems, and other applications involving heat transfer in fluid flow.
Learn more about Prandtl number here:
https://brainly.com/question/32353670
#SPJ11
The data on the right represent the number of live multiple-delivery births (three or more babies) in a particular year for women 15 to 54 years old. Use the data to complete parts (a) through (d) below.
Age 15-19 20-24 25-29 30-34 35-39 40 44 45-54 Number of Multiple Births 89 508 1631 2822 1855 374 119 (a) Determine the probability that a randomly selected multiple birth for women 15-54 years old involved a mother 30 to 39 years old P(30 to 39) =______
(Type an integer or decimal rounded to three decimal places as needed.)
(b) Determine the probability that a randomly selected multiple birth for women 15-54 years old involved a mother who was not 30 to 39 years old. P(not 30 to 39)=_____ (Type an integer or decimal rounded to three decimal places as needed.) (c) Determine the probability that a randomly selected multiple birth for women 15-54 years old involved a mother who was less than 45 years old. P(less than 45)=_____
(Type an integer or decimal rounded to three decimal places as needed.) (d) Determine the probability that a randomly selected multiple birth for women 15-54 years old involved a mother who was at least 40 years old. Interpret this result. Is it unusual? Find the probability that a randomly selected multiple birth for women 15-54 years old involved a mother who was at least 40 years old. P(at least 40) =_____ (Type an integer or decimal rounded to three decimal places as needed.) Interpret this result. Select the correct choice below and fill in the answer box to complete your choice. (Type a whole number.) A. If 1000 multiple births for women 15-54 years old were randomly selected, we would expect about of them to involve a mother who was at least 40 years old. B. If 1000 multiple births for women 15-54 years old were randomly selected, exactly of them would involve a mother who was at least 40 years old. Is a multiple birth involving a mother who was at least 40 years old unusual? A. Yes, because the probability of a multiple birth involving a mother who was at least 40 years old is greater than 0.05.
B. Yes, because the probability of a multiple birth involving a mother who was at least 40 years old is less than 0.05. C. No, because the probability of a multiple birth involving a mother who was at least 40 years old is greater than 0.05. D. No, because the probability of a multiple birth involving a mother who was at least 40 years old is less than 0.05.
Answers
Using the given data on the number of live multiple-delivery births for women aged 15 to 54, we need to calculate probabilities related to the age groups of the mothers. The probability of a randomly selected multiple birth involving a mother aged 30 to 39 will be determined, as well as the probabilities of not being in the age range, being less than 45, and being at least 40. Finally, we need to interpret whether a multiple birth involving a mother aged at least 40 is unusual.
(a) To calculate the probability of a randomly selected multiple birth involving a mother aged 30 to 39, we sum the number of multiple births in that age group and divide it by the total number of multiple births for women aged 15 to 54.
P(30 to 39) = 2822 / (89 + 508 + 1631 + 2822 + 1855 + 374 + 119)
(b) To find the probability of a randomly selected multiple birth involving a mother who is not aged 30 to 39, we subtract the probability found in part (a) from 1.
P(not 30 to 39) = 1 - P(30 to 39)
(c) To determine the probability of a randomly selected multiple birth involving a mother aged less than 45, we sum the number of multiple births for age groups below 45 and divide it by the total number of multiple births for women aged 15 to 54.
P(less than 45) = (89 + 508 + 1631 + 2822 + 1855 + 374) / (89 + 508 + 1631 + 2822 + 1855 + 374 + 119)
(d) To find the probability of a randomly selected multiple birth involving a mother aged at least 40, we sum the number of multiple births for age groups 40-44 and 45-54, and divide it by the total number of multiple births for women aged 15 to 54.
P(at least 40) = (374 + 119) / (89 + 508 + 1631 + 2822 + 1855 + 374 + 119)
Interpretation: The answer to part (d) will determine whether a multiple birth involving a mother aged at least 40 is unusual. If the probability is less than 0.05, it can be considered unusual. Therefore, we need to compare the calculated probability to 0.05 and select the correct choice.
To know more about probability here: brainly.com/question/32117953
#SPJ11
Solve:
3x-5/2 +x+ 2x-3/3 = 5/6 - 3x/2
Answers
Answer:
x = 26/45
Step-by-step explanation:
Answer:
Given Question
Solve for x :
\(\rm :\longmapsto\:\dfrac{3x - 5}{2} + x + \dfrac{2x - 3}{3} = \dfrac{5}{6} - \dfrac{3x}{2} \)
\( \green{\large\underline{\sf{Solution-}}}\)
Given expression is
\(\rm :\longmapsto\:\dfrac{3x - 5}{2} + x + \dfrac{2x - 3}{3} = \dfrac{5}{6} - \dfrac{3x}{2} \)
On taking LCM of (2 and 3 = 6) on LHS and Taking LCM of ( 2 and 6 = 6) on RHS, we get\(\rm :\longmapsto\:\dfrac{3(3x - 5) + 6x + 2(2x - 3)}{6} = \dfrac{5 - 9x}{6}\)
\(\rm :\longmapsto\:9x - 15 + 6x + 4x - 6 = 5 - 9x\)
\(\rm :\longmapsto\:(9x + 6x + 4x) - 15 - 6 = 5 - 9x\)
\(\rm :\longmapsto\:19x - 21 = 5 - 9x\)
\(\rm :\longmapsto\:19x + 9x = 5 + 21\)
\(\rm :\longmapsto\:28x = 26\)
\(\rm :\longmapsto\:x = \dfrac{26}{28} \)
\(\bf\implies \:x = \dfrac{13}{14} \)
VERIFICATIONConsider LHS
\(\rm :\longmapsto\:\dfrac{3x - 5}{2} + x + \dfrac{2x - 3}{3}\)
On substituting the value of x, we get
\(\rm \: = \: \dfrac{\dfrac{39}{14} - 5}{2} + \dfrac{13}{14} + \dfrac{\dfrac{13}{7} - 3}{3}\)
\(\rm \: = \: \dfrac{39- 70}{28} + \dfrac{13}{14} + \dfrac{13 - 21}{21}\)
\(\rm \: = \: \dfrac{ - 31}{28} + \dfrac{13}{14} - \dfrac{8}{21}\)
\(\rm \: = \: \dfrac{ - 31 + 26}{28} - \dfrac{8}{21}\)
\(\rm \: = \: \dfrac{ -5}{28} - \dfrac{8}{21}\)
\(\rm \: = \: \dfrac{ -15 - 32}{84}\)
\(\rm \: = \: - \: \dfrac{47}{84}\)
Consider RHS
\(\rm :\longmapsto\: \dfrac{5}{6} - \dfrac{3x}{2} \)
On substituting the value of x, we get
\( \rm \: = \: \dfrac{5}{6} - \dfrac{39}{28} \)
\( \rm \: = \: \dfrac{70 - 117}{84}\)
\( \rm \: = \: - \dfrac{47}{84}\)
Hence, LHS = RHS
Hence, Verified.
histograms: answer a and b, find median and lower quartile
Answers
Answer:
A)median score = 116
b)lower quartile= 102
Find the diameter of a circle with a circumference of 167 yards.
32
4
8.
O 16
HELP PLEASE!!
Answers
Determine the nature of the roots of ax² + bx + c = 0 if a > 0, b < 0 and c < 0
Answers
Answer: Roots are real and distinct
Step-by-step explanation:
a = +ve b = -ve c = -ve
determinant = +ve
if determinant is positive then roots are real and distinct
How many powers of 7 are contained in 10?
Answers
There is only 1 power of 7 contained in 10.
Students use powers of numbers to solve this problem and learn what is occurring to the numbers as a result.
Students also learn how to divide a seemingly vast and challenging equation into smaller, more accessible components. The pupils should understand that raising 7 to a power only produces a finite number of unit digits. Furthermore, as the power of 7 rises, these particular numbers "circle round." 7, 9, 3, and 1 make up this cycle.
The digit in the tens place is the same.
The total number of times we multiply a number is known as its exponent or power. For instance, 2 to the power 3 denotes a 3x3 multiplication of 2.
The largest power of 7 that is less than 10 is 7^1 = 7, therefore there is only 1 power of 7 contained in 10.
To know more about exponents visit :
https://brainly.com/question/30066987?referrer=searchResults
#SPJ4
There is only 1 power of 7 contained in 10.
Students use powers of numbers to solve this problem and learn what is occurring to the numbers as a result.
Students also learn how to divide a seemingly vast and challenging equation into smaller, more accessible components. The pupils should understand that raising 7 to a power only produces a finite number of unit digits. Furthermore, as the power of 7 rises, these particular numbers "circle round." 7, 9, 3, and 1 make up this cycle.
The digit in the tens place is the same.
The total number of times we multiply a number is known as its exponent or power. For instance, 2 to the power 3 denotes a 3x3 multiplication of 2.
The largest power of 7 that is less than 10 is 7^1 = 7, therefore there is only 1 power of 7 contained in 10.
To know more about exponents visit :
brainly.com/question/30066987?referrer=searchResults
#SPJ4
PLEASE HELP I DO NOT UNDERSTAND THIS
Answers
Answer:a=20 b=16 c=18
Step-by-step explanation:
the ration 4/3 , a=15*4/3=20 b=12*4/3=16. C=24/4/3=18
The population on a certain island increased from 1500 in 2000 to 1577 in 2001 a. Determine the growth rate b. Write a general equation for the popolation p(t) c. Estimate the population in 2010 d. How many years will it take for the population to double?
Answers
Therefore, it will take approximately 13.7 years for the population to double.
a. To determine the growth rate, you need to calculate the percentage increase in population. The formula for growth rate is:
Growth Rate = (New Value - Old Value) / Old Value * 100
Using the given values, we have:
Growth Rate = (1577 - 1500) / 1500 * 100
Growth Rate = 77 / 1500 * 100
Growth Rate ≈ 5.13%
b. To write a general equation for the population, you can use the formula:
p(t) = p(0) * (1 + r/100)^t
where p(t) is the population at time t, p(0) is the initial population, r is the growth rate, and t is the number of years.
c. To estimate the population in 2010, we need to find the population at time t = 2010 - 2000 = 10 years. Using the general equation from part b, and substituting the given values:
p(10) = 1500 * (1 + 5.13/100)^10
p(10) ≈ 1500 * (1.0513)^10
p(10) ≈ 1500 * 1.6436
p(10) ≈ 2465.4
Therefore, the estimated population in 2010 is approximately 2465.
d. To find out how many years it will take for the population to double, we need to solve the equation:
2 * p(0) = p(0) * (1 + r/100)^t
Simplifying the equation, we have:
2 = (1 + r/100)^t
Taking the logarithm of both sides, we get:
log(2) = t * log(1 + r/100)
Finally, solving for t, we have:
t = log(2) / log(1 + r/100)
Substituting the growth rate from part a, we have:
t = log(2) / log(1 + 5.13/100)
t ≈ log(2) / log(1.0513)
t ≈ 13.7 years
Therefore, it will take approximately 13.7 years for the population to double.
To know more about population visit :
https://brainly.com/question/19169926
#SPJ11
what is the rule for the reflection
Answers
Step-by-step explanation:
We reflect We triangle across both axis so the x and y values will both switch.
Our triangle is originally in the second quadrant but then go to the 4the after we reflect it.
Second Quadrant are
^;8+1—](
Grade 10 Math. Solve for y. Will mark right answer brainliest :)
Answers
Answer:
y=5, y=\(\frac{38}{11}\)
Step-by-step explanation:
Hi there!
We are given the equation
\(\frac{y+2}{y-3}\)+\(\frac{y-1}{y-4}\)=\(\frac{15}{2}\) and we need to solve for y
first, we need to find the domain, which is which is the set of values that y CANNOT be, as the denominator of the fractions cannot be 0
which means that y-3≠0, or y≠3, and y-4≠0, or y≠4
\(\frac{y+2}{y-3}\) and \(\frac{y-1}{y-4}\) are algebraic fractions, meaning that they are fractions (notice the fraction bar), but BOTH the numerator and denominator have algebraic expressions
Nonetheless, they are still fractions, and we need to add them.
To add fractions, we need to find a common denominator
One of the easiest ways to find a common denominator is to multiply the denominators of the fractions together
Let's do that here;
on \(\frac{y+2}{y-3}\), multiply the numerator and denominator by y-4
\(\frac{(y+2)(y-4)}{(y-3)(y-4)}\); simplify by multiplying the binomials together using FOIL to get:
\(\frac{y^{2}-2y-8}{y^{2}-7y+12}\)
Now on \(\frac{y-1}{y-4}\), multiply the numerator and denominator by y-3
\(\frac{(y-1)(y-3)}{(y-4)(y-3)}\); simplify by multiplying the binomials together using FOIL to get:
\(\frac{y^{2}-4y+3}{y^{2}-7y+12}\)
now add \(\frac{y^{2}-2y-8}{y^{2}-7y+12}\) and \(\frac{y^{2}-4y+3}{y^{2}-7y+12}\) together
Remember: since they have the same denominator, we add the numerators together
\(\frac{y^{2}-2y-8+y^{2}-4y+3}{y^{2}-7y+12}\)
simplify by combining like terms
the result is:
\(\frac{2y^{2}-6y-5}{y^{2}-7y+12}\)
remember, that's set equal to \(\frac{15}{2}\)
here is our equation now:
\(\frac{2y^{2}-6y-5}{y^{2}-7y+12}\)=\(\frac{15}{2}\)
it is a proportion, so you may cross multiply
2(2y²-6y-5)=15(y²-7y+12)
do the distributive property
4y²-12y-10=15y²-105y+180
subtract 4y² from both sides
-12y-10=11y²-105y+180
add 12 y to both sides
-10=11y²-93y+180
add 10 to both sides
11y²-93y+190=0
now we have a quadratic equation
Let's solve this using the quadratic formula
Recall that the quadratic formula is y=(-b±√(b²-4ac))/2a, where a, b, and c are the coefficients of the numbers in a quadratic equation
in this case,
a=11
b=-93
c=190
substitute into the formula
y=(93±√(8649-4(11*190))/2*11
simplify the part under the radical
y=(93±√289)/22
take the square root of 289
y=(93±17)/22
split into 2 separate equations:
y=\(\frac{93+17}{22}\)
y=\(\frac{110}{22}\)
y=5
and:
y=\(\frac{93-17}{22}\)
y=\(\frac{76}{22}\)
y=\(\frac{38}{11}\)
Both numbers work in this case (remember: the domain is y≠3, y≠4)
So the answer is:
y=5, y=\(\frac{38}{11}\)
Hope this helps! :)
a spherical balloon has volume v and radius r . by what factor is its radius reduced if you let enough air out of the balloon to reduce its volume by a factor of 27.0?
Answers
The factor of its radius reduced is 3. The result is obtained by comparing the spherical volumes.
What is the formula for a spherical volume?The volume of a spherical can be calculated by
V = 4/3 πr³
Where
V = volumeπ = 3.14 or 22/7r = radius of sphereA spherical balloon has volume v and radius r. Its volume is reduced by a factor of 27.0.
Find the factor of its radius reduced!
The factor of its volume is
V₁/V₂ = 27
We use the formula for spherical volume to find r₁/r₂.
V₁/V₂ = (4/3 πr₁³)/(4/3 πr₂³)
27 = (r₁/r₂)³
r₁/r₂ = ∛27
r₁/r₂ = 3
Hence, the radius is reduced by a factor of 3.
Learn more about volume of a sphere here:
brainly.com/question/9994313
#SPJ4
Area of lawn pls don’t send link for a website and explain here
Answers
Answer:
area of lawn = 15.708 square meters
Step-by-step explanation:
pi 3 squared (area of lawn and flower bed) - pi 2 squared (area of flower bed)= area of lawn
A 12-sided solid has faces numbered 1 to 12. The table shows the results of rolling the solid 200 times. Find the experimental probability of rolling a number less than 3
Answers
The experimental probability of rolling a number less than 3 is 0.11 or 11% when rolling a 12-sided solid numbered from 1 to 12, based on the provided data.
The number of faces that are numbered less than 3 on a 12-sided solid is 2, i.e., 1 and 2. Therefore, the probability of rolling a number less than 3 can be calculated by adding the frequencies of rolls that resulted in 1 and 2, and then dividing the sum by the total number of rolls.
From the table, we can see that the frequency of rolling a 1 is 10 and the frequency of rolling a 2 is 12. Therefore, the total frequency of rolling a number less than 3 is 10 + 12 = 22.
The total number of rolls is 200.
The experimental probability of rolling a number less than 3 is the frequency of rolling a number less than 3 divided by the total number of rolls:
Experimental probability = Frequency of rolling a number less than 3 / Total number of rolls
Experimental probability = 22 / 200
Experimental probability = 0.11
For such more questions on probability
https://brainly.com/question/25839839
#SPJ8
Dell Eatery employs one worker whose job it is to load apple pies on outgoing company cars. Cars arrive at the loading gate at an average of 48 per day, or 6 per hour, according to a Poisson distribution. The worker loads them at a rate of 8 per hour, following approximately the exponential distribution in service times. a. Determine the operating characteristics of this loading gate problem. [6 Marks] b. What is the probability that there will be more than six cars either being loaded or waiting? [2 Marks] Formulae L= μ−λ
λ
W= μ−λ
1
L q
W q
rho
P 0
= μ(μ−λ)
λ 2
= μ(μ−λ)
λ
= μ
λ
=1− μ
λ
P n>k
=( μ
λ
) k+1
Answers
The required probability is 0.4408.
The operating characteristics of the loading gate problem are:
L = λ/ (μ - λ)
W = 1/ (μ - λ)
Lq = λ^2 / μ (μ - λ)
Wq = λ / μ (μ - λ)
ρ = λ / μ
P0 = 1 - λ / μ
Where, L represents the average number of cars either being loaded or waiting.
W represents the average time a car spends either being loaded or waiting.
Lq represents the average number of cars waiting.
Wq represents the average waiting time of a car.
ρ represents the utilization factor.
ρ = λ / μ represents the ratio of time the worker spends loading cars to the total time the system is busy.
P0 represents the probability that the system is empty.
The probability that there will be more than six cars either being loaded or waiting is to be determined. That is,
P (n > 6) = 1 - P (n ≤ 6)
Now, the probability of having less than or equal to six cars in the system at a given time,
P (n ≤ 6) = Σn = 0^6 [λ^n / n! * (μ - λ)^n]
Putting the values of λ and μ, we get,
P (n ≤ 6) = Σn = 0^6 [(6/ 48)^n / n! * (8/ 48)^n]
P (n ≤ 6) = [(6/ 48)^0 / 0! * (8/ 48)^0] + [(6/ 48)^1 / 1! * (8/ 48)^1] + [(6/ 48)^2 / 2! * (8/ 48)^2] + [(6/ 48)^3 / 3! * (8/ 48)^3] + [(6/ 48)^4 / 4! * (8/ 48)^4] + [(6/ 48)^5 / 5! * (8/ 48)^5] + [(6/ 48)^6 / 6! * (8/ 48)^6]P (n ≤ 6) = 0.5592
Now, P (n > 6) = 1 - P (n ≤ 6) = 1 - 0.5592 = 0.4408
Therefore, the required probability is 0.4408.
Learn more about loading gate visit:
brainly.com/question/33562503
#SPJ11
Find the value of the constant k such that the function is a probability density function on the indicated interval. f(x) = k√x; (0,9) k =
Answers
The value of the constant k for the function to be a probability density function on the interval (0, 9) is k = 1/18.
To find the value of the constant k such that the function \(f(x) = k\sqrt{x}\) is a probability density function on the interval (0, 9), you need to make sure that the total probability is equal to 1. This means that the integral of f(x) from 0 to 9 must be equal to 1.
Step 1: Write the integral for the function f(x) from 0 to 9.
∫(0 to 9) k√x dx
Step 2: Find the antiderivative of k√x with respect to x.
Antiderivative of \(k\sqrt{x} =\frac{2}{3} k x^{\frac{3}{2} }\)
Step 3: Evaluate the antiderivative at the limits 0 and 9.
((2/3)k(9)^(3/2)) - ((2/3)k(0)^(3/2)) = (2/3)k(27) - 0 = (2/3)k(27)
Step 4: Set the integral equal to 1 and solve for k.
(2/3)k(27) = 1
k = 1 / (2/3 * 27) = 1 / 18
So, the value of the constant k for the function to be a probability density function on the interval (0, 9) is k = 1/18.
To know more about "PROBABILITY DENSITY FUNCTION" refer here:
https://brainly.com/question/30403935#
#SPJ11
How do you determine a rational number calculate?
Answers
If all the numbers involved are rational, then the result will be rational. If one or more of the numbers are irrational, the result may or may not be rational, depending on the specific numbers involved in the calculation.
A rational number is a number that can be expressed as a ratio of two integers, where the denominator is not zero. In this answer, we will explain how to determine whether a calculation involving numbers results in a rational number or not.
To determine whether a calculation results in a rational number or not, we need to follow a few steps. First, we need to identify the numbers involved in the calculation. If all the numbers are rational, then the result will also be rational.
However, if one or more of the numbers involved in the calculation is not a rational number, then the result may or may not be a rational number. For example, if we divide a rational number by an irrational number, the result will be an irrational number. This is because dividing a rational number by an irrational number results in a number that cannot be expressed as a ratio of two integers.
On the other hand, if we multiply a rational number by an irrational number, the result may or may not be a rational number. It depends on the specific numbers involved in the calculation.
To know more about rational number here.
https://brainly.com/question/24540810
#SPJ4
Complete Question:
How do you solve rational number calculation?
we find t=2.73 with 5 degrees of freedom. what is the appropriate p-value.
Answers
The appropriate p-value for a t-value of 2.73 with 5 degrees of freedom is approximately 0.05. This indicates that there is a 5% chance of observing a t-value as extreme as 2.73 or more extreme, assuming the null hypothesis is true.
In statistics, the p-value measures the strength of evidence against the null hypothesis. The null hypothesis states that there is no significant difference or effect in the population being studied. The p-value is calculated by determining the probability of obtaining a test statistic (in this case, the t-value) as extreme as or more extreme than the observed value, assuming the null hypothesis is true.
To determine the appropriate p-value for a t-value, we typically consult a t-distribution table or use statistical software. In this case, with 5 degrees of freedom and a t-value of 2.73, we look up the critical value or use software to find the corresponding p-value. The p-value associated with a t-value of 2.73 and 5 degrees of freedom is approximately 0.05.
The p-value of 0.05 indicates that there is a 5% chance of obtaining a t-value as extreme as 2.73 or more extreme, assuming the null hypothesis is true. Generally, a p-value of 0.05 or lower is considered statistically significant, implying that the observed result is unlikely to have occurred by chance alone. If the p-value is below a predetermined significance level (often denoted as α, commonly set at 0.05), we reject the null hypothesis in favor of an alternative hypothesis. If the p-value is above the significance level, we fail to reject the null hypothesis.
Learn more about Null hypothesis:
brainly.com/question/19263925
#SPJ11
QUESTION 5
Given the following two functions:
f(x)=x2+1 and g(x)=x+ 1, find (g+f) (-1)
Answers
Answer:
(g+f)(-1)=2
Step-by-step explanation:
f(x)x²+1
g(x)=x+1
(g+f)(x)= x+1+x²+1
(g+f)(-1)=(-1)+1(-1)²+1
(g+f)(-1)=(-1)+1+(-1)²+1
(g+f)(-1)=2
Hope this helps u! :)
expand 3a(2b+c) .............
Answers
Answer:
We know that the distributive property says this:
a(b+c) = ab + ac
If we apply this to our case, we can put
3a(2b+c) = 3a * 2b + 3a * c
When we multiply numbers and letters, we should multiply both of them:
3a * 2b + 3a * c = 3*2*a*b + 3*a*c = 6ab +3ac
We can use this when we find a number multiplied by a parenthesis..
Answer:
6ab + 3ac
Step-by-step explanation:
3a(2b) + 3a(c)
6ab + 3ac
Complete the square. Fill in the number that makes the polynomial a perfect-square quadratic. X2+82x+
Answers
In completing the square method, considering the equation X^2 + 82x + the number to be added should be 1681 to make it a perfect square
How to know term that should addedThe quadratic equation is an equation of the form
ax^2 + bx + c
The completing the square method is on of the methods of solving equations of the form above
The factor to be added on the both sides of the equation while using the completing the square method is
(b / 2a)^2
compared to the equation in the problem X^2 +82x
= (b / 2a)^2
= (82 / 2)^2
= (41)^2
= 1681
Learn more on quadratic equations here:
https://brainly.com/question/29227857
#SPJ1
how many hours can cold food be held without refrigeration before it must be sold, served, or thrown out?
Answers
Quinn has assets of $50,000 and liabilities of $22,000. What is Quinn's net worth?
O $22,000
O $24,000
O $28,000
O $77,000
Please help me :,)
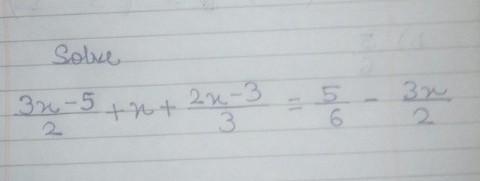
Answers
Pls help i will give 5 starts and brainliest question is down below 9:22
Answers
Answer:
D
Step-by-step explanation:
I have done this before
Top row units is 8 i then multiplied both sides so 5*2 which = 10 then multiplied 8*10 to get 80
Answer:
80 square units (D)
Step-by-step explanation:
Base is 16 units, height is 5 units. 16 * 5 = 80