John gets a new job and receives a $500 signing bonus. After that, he makes $200 a day. How much money does he make after 4 days?
Answers
Answer:
John makes a total of $1,300.
Step-by-step explanation:
We know that before his bonus, John already has $500. Then, he gets $200 every day for 4 days.
200 x 4 = $800
So, over the course of those 4 days, Johnny makes $800. Now, let's add this to the rest of his money.
800 + 500 = $1,300
Therefore, John makes a total of $1,300.
Hope this helps! :)
Related Questions
suppose that the average country song length in america is 4.75 minutes with a standard deviation of 1.10 minutes. it is known that song length is not normally distributed. suppose a sample of 25 songs is taken from the population. what is the approximate probability that the average song length will last more than 5.25 minutes? round to the nearest thousandth.
Answers
Answer:
4.75
+1.10
5.85
25
5.60
5.25
0.35
lines a and b are parallel in the diagram what is the measure of angle 1

Answers
Answer:
45
Step-by-step explanation:
Upon examining the graph, you can realize that angle 3x is the same as the angle directly to the left of 9x. Since that makes a straight line, we can realize that that sums up to 180. We call this a linear pair.
so you have:
3x+9x = 12x = 180
x = 15
A important concept to know here is vertical angles. Vertical angles occur when two lines intersect each other. The opposite angles formed at an intersection are congruent, which is why 1 is congruent to 3x.
Therefore, angle 1 is 45 degrees.
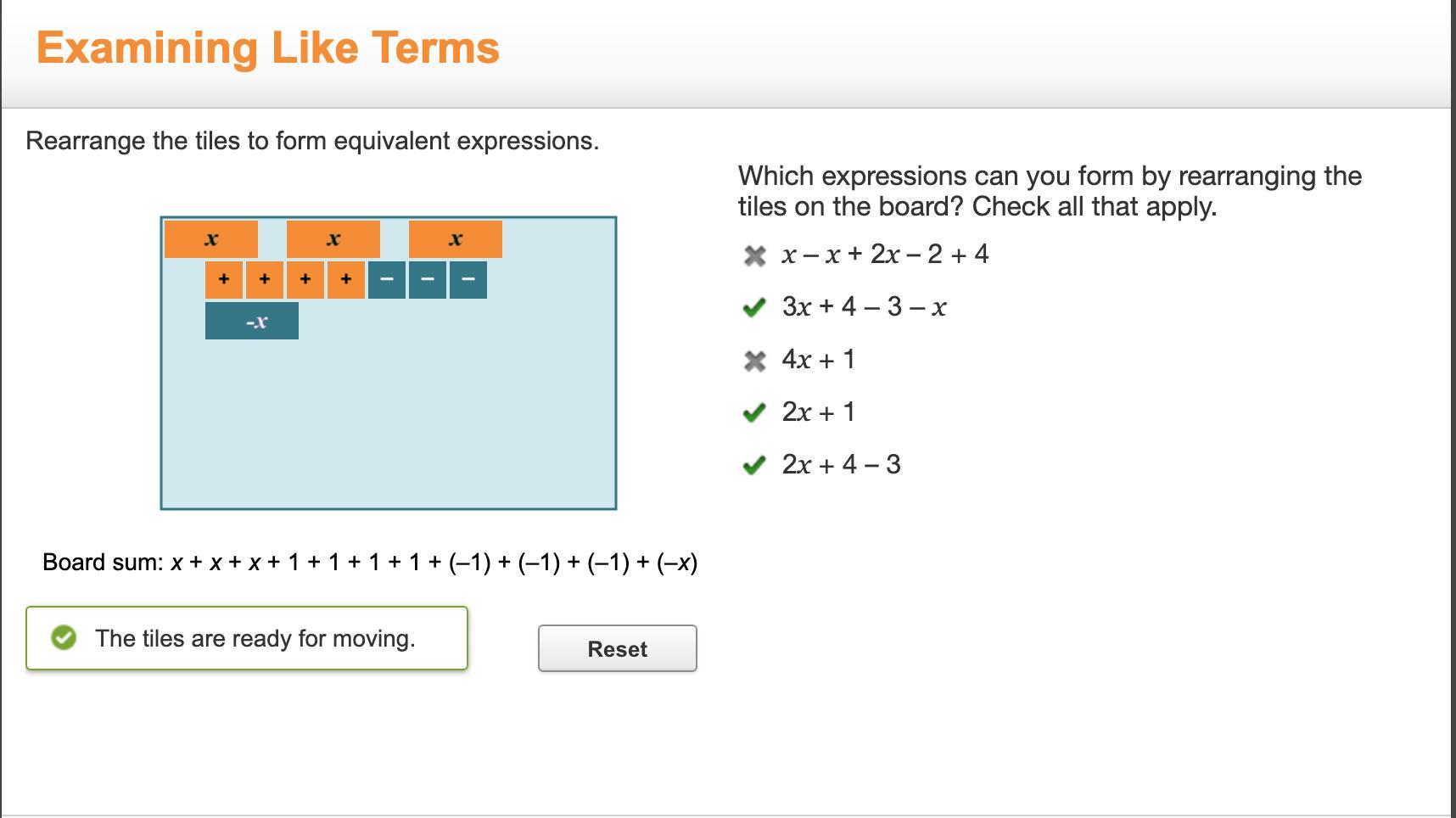
Which expressions can you form by rearranging x+x+x+1+1+1+1+(-1)+(-1)+(-1)+(-x) Check all that apply.
A) x – x + 2x – 2 + 4
B) 3x + 4 – 3 – x
C) 4x + 1
D) 2x + 1
E) 2x + 4 – 3
Answers
Answer:
The correct options are;
B) 3x + 4 – 3 – x
D) 2x + 1
E) 2x + 4 – 3
Step-by-step explanation:
Which expressions can you form by rearranging x+x+x+1+1+1+1+(-1)+(-1)+(-1)+(-x) Check all that apply.
A) x – x + 2x – 2 + 4
B) 3x + 4 – 3 – x
C) 4x + 1
D) 2x + 1
E) 2x + 4 – 3
x+x+x+1+1+1+1+(-1)+(-1)+(-1)+(-x)
positive sign multiply by negative sign will give a negative sign, hence;
x+x+x+1+1+1+1-1-1-1-x
Rearranging the equation;
x + x + x -x+ 1+1+1+1 -1-1-1
=3x -x + 4 -3
=2x + 1
We can also re-arrange it to give 3x + 4 - 3 -x
because
3x + 4 -3 -x
=3x -x + 4 -3
=2x + 1
Also, we can re-arrange it to give 2x + 4 - 3
since 2x + 4 - 3 = 2x + 1
The correct options are;
B) 3x + 4 – 3 – x
D) 2x + 1
E) 2x + 4 – 3
Answer:
Step-by-step explanation:
HELP ME PLEASEE TYYY

Answers
Answer: y-intercept=(0,19).
Drag the numbers to order them from least to greatest.
1/5
-0.4
-2 1/3
65%

Answers
1/5 is .2 and 65% is .65
from least to greatest this would be -2 1/3 , -.4 , 1/5, 65%
Answer:
-2 1/3, -0.4, 1/5 65%
Step-by-step explanation:
I think that's correct
how does a qualitative graph describe the relationship between quantities
Answers
As described in Analytical Geometry the relationship between quantities of a qualitative graph are explained below.
What is Analytical Geometry?
The area of algebra known as analytical geometry uses an ordered pair of numbers known as coordinates to determine the position of a point on a plane. It is utilised to model many plane objects, including points, lines, and others. The terms Coordinate geometry and Cartesian geometry are both used to refer to analytical geometry.
Cluster Use functions to model relationships between quantities. Standard Describe qualitatively the functional relationship between two quantities by analyzing a graph (e.g., where the function is increasing or decreasing, linear or nonlinear).
A linear relationship between two quantities will produce a graph of a straight line. The line represents every possible solution for the range of the function. In order to create the line, we use the function equation and evaluate the range, or output, values based upon several of the domain, or input, values.
To learn more about analytical geometry from the given link
https://brainly.com/question/23036034
#SPJ1
Circle the equivalent expressions: A. 3(2p + 2) B. 12p C. p(3 + 3) + 6 D. 5p + 6 E. 2p + 4p + 6 F. 3 + 6p + 3
Answers
Answer:
a,e,f
Step-by-step explanation:
a. 6p+6
b.12p
c.6p
d.5p+6
e.6p+6
f.6p+6
223
can be thought of as a whole number and a fraction.
Complete the statements below to show the number of wholes and the fractional part that make up 223
.
Answers
The second statement is the most commonly used way of writing 223 as a combination of a whole number and a fraction, but there are many other ways to express it.
What is a fraction ?
A fraction is a mathematical concept used to represent a part of a whole. It is represented by two numbers separated by a line, called a fraction bar or a solidus. The number above the line is called the numerator, and the number below the line is called the denominator
223 can be written as:
223 wholes and 0/1 as the fraction
222 wholes and 1/1 as the fraction
221 wholes and 2/1 as the fraction
...
0 wholes and 223/1 as the fraction
Note that
Therefore, the second statement is the most commonly used way of writing 223 as a combination of a whole number and a fraction, but there are many other ways to express it.
To learn more about Fraction from given link.
https://brainly.com/question/10708469
#SPJ1
a(n) ____ is a transformation in which the size or the shape of a geometric figure is changed.
Answers
Dilations involve scaling the figure uniformly along a given center and factor. This process results in an enlarged or reduced version of the original figure, while maintaining the same proportions and shape.
A dilation is a type of geometric transformation that alters the size or shape of a figure while preserving its proportions. It involves scaling the figure uniformly in all directions from a specific center of dilation. The scaling factor determines whether the figure will be enlarged or reduced.
When dilating a figure, each point is moved along a line that passes through the center of dilation. The distance between the original point and the center is multiplied by the scaling factor to determine the new position of the point. If the scaling factor is greater than 1, the figure will be enlarged, while a scaling factor between 0 and 1 will result in a reduction.
The center of dilation can be any point on the plane, and it serves as the reference point from which the scaling occurs. If the center of dilation is outside the figure, the shape will change along with the size. However, if the center is inside the figure, only the size will be affected, and the shape will remain the same.
Learn more about geometric figure: brainly.com/question/31178455
#SPJ11
What is the equation on the line

Answers
Answer:
(1,1)
Step-by-step explanation:
The line is on the point
assume that for some statistic 1000 tests were performed. to avoid the situation of the incorrectly found significance, bonferroni correction was applied. the resulting p-value is 0.00013. what significance level was chosen for the tests? the significance level was:
Answers
The significance level chosen for the tests with total number of test performed as 1000 for given p-value is equal to 0.87 or 87%.
Total number of test performed = 1000
p-value is equal to 0.00013
The Bonferroni correction involves ,
Adjusting the significance level for multiple comparisons by dividing it by the number of comparisons performed.
Here, 1000 tests were performed and the resulting p-value is 0.00013.
The significance level that was chosen for the tests,
Reverse the Bonferroni correction by multiplying the p-value by the number of comparisons,
adjusted p-value = p-value / number of comparisons
number of comparisons = 1000
adjusted p-value = 0.00013
p-value = adjusted p-value x number of comparisons
⇒p-value = 0.00013 x 1000
⇒p-value = 0.13
So the original p-value before the Bonferroni correction was 0.13.
The significance level, we subtract the p-value from 1,
significance level = 1 - p-value
⇒significance level = 1 - 0.13
⇒significance level = 0.87
Therefore, the significance level chosen for the tests was 0.87 or 87%
learn more about significance level here
brainly.com/question/3487014
#SPJ4
Drag the tiles to the correct boxes to complete
pairs.
Given: U = <-2, -7>, V = <3,-4>, and w=<5, 1>
Based on the components of the given vectors, match each vector subtraction with the graph of the resulting vector.

Answers
Answer:
your correct answer is option ( A )
Answer:
graph 1 ----> u-v
graph 2 ----> u-w
graph 3 ----> w-v
graph 4 ----> v-u
Step-by-step explanation:
Made 100% on plato

1. Find the general solution to 4y′′+y=2sec(t/2) 2. Consider the ODE t2y′′−2y=3t2−1,t>0 (a) Show that t2 and t−1 are a fundamental set of solutions for the associated homogenous equation. (b) Find the particular solution to the equation (DO NOT FIND THE GENERAL SOLUTION).
Answers
The general solution to the differential equation 4y'' + y = 2sec(t/2) is y(t) = c1cos(t/2) + c2sin(t/2) + 2sec(t/2). For the associated homogeneous equation t²y'' - 2y = 0, t² and \(t^{(-1)\) are a fundamental set of solutions.
To find the general solution to the differential equation 4y'' + y = 2sec(t/2), we can first find the complementary solution by solving the associated homogeneous equation 4y'' + y = 0.
The characteristic equation is r² + 1/4 = 0. Solving this equation, we get r = ±i/2. Therefore, the complementary solution is given by \(y_c\)(t) = c1cos(t/2) + c2sin(t/2), where c1 and c2 are arbitrary constants.
Next, we find a particular solution to the non-homogeneous equation. Since the right-hand side is 2sec(t/2), we can guess a particular solution of the form \(y_p\)(t) = A×sec(t/2), where A is a constant to be determined.
We differentiate \(y_p\)(t) twice and substitute into the differential equation to find the value of A. After simplification, we find that A = 2.
Therefore, the particular solution is \(y_p\)(t) = 2sec(t/2).
The general solution is the sum of the complementary solution and the particular solution:
y(t) = \(y_c\)(t) + \(y_p\)(t) = c1cos(t/2) + c2sin(t/2) + 2sec(t/2).
(a) To show that t² and \(t^{(-1)\) are a fundamental set of solutions for the associated homogeneous equation t²y'' - 2y = 0, we need to show that they are linearly independent solutions.
We can start by assuming that there exist constants c1 and c2 such that c1t² + c2\(t^{(-1)\) = 0 for all t > 0. This implies that c1t² = -c2\(t^{(-1)\).
Taking the derivative twice, we get 2c1 - 2c2\(t^{(-3)\) = 0. Integrating twice, we find c1t² + c3 = 0, where c3 is an integration constant.
If c1 is non-zero, then the equation c1×t² + c3 = 0 cannot hold for all t > 0, which contradicts our assumption. Therefore, c1 must be zero.
If c2 is non-zero, then the equation c2×\(t^{(-1)\) = 0 cannot hold for all t > 0, which contradicts our assumption. Therefore, c2 must be zero.
Since both c1 and c2 must be zero, t² and \(t^{(-1)\) are linearly independent solutions, making them a fundamental set of solutions.
(b) To find the particular solution to the equation t²y'' - 2y = 3t² - 1, we can use the method of undetermined coefficients.
We guess a particular solution of the form \(y_p\)(t) = At² + Bt + C, where A, B, and C are constants to be determined.
We differentiate \(y_p\)(t) twice and substitute them into the differential equation to find the values of A, B, and C. After simplification, we find A = 1 and B = 0.
Therefore, the particular solution is \(y_p\)(t) = t² + C.
Learn more about the general solution at
https://brainly.com/question/32062078
#SPJ4
Two trains, train A and train B, weigh a total of 526 tons. Train A is heavier than train B. The difference of their weights is 368 tons. what is the weight of each train? How much does train A weigh?
Answers
Laquan will give each guest at his party ¹⁄₂ of a cake. How many cakes should he order if 17 people are attending his party?
Answers
Answer:
9 cakes
Step-by-step explanation:
If each of the 17 people will eat 1/2 of a cake, you would 17*1/2 cakes. This is 17/2, or 8.5. You cannot usually order 8.5 cakes, so you would round up. 9 cakes.
Question 1 1 pts If g and h are both positive numbers, which statement is true about the x-intercepts of the function f(x) = (x - g)(x - h). the function has no x-intercepts both x-intercepts are negative one x-intercept is negative and one x-intercept is positive both x-intercepts are positive
Answers
for the function
f(x) = (x -g)(x - h)
To get the x-intercept, we can equate the function to zero
f(x) = (x -g)(x - h) = 0
so (x - g) = 0
which gives x = g
And (x - h) = 0
which gives x = h
Since we have been told that g and h are positive, then it follows that both intercepts are positive
The sales tax in mikes home city is 8.25% mike buys a sweater for 49.95
Answers
Answer:
54.07
Step-by-step explanation:
can anyone answer this with expanation?

Answers
18. ∆PQR =~ ∆RPA ( by SAS )
19. ∆DQR =~ ∆PQR ( by AAS )
20. ∆ARO =~ ∆PQO ( by AAS )
96 out of 200 animals treated by a veterinarian are horses. Write 96/200 as a decimal and as a percent.
Answers
Answer:
0.48
48%
Step-by-step explanation:
\( \frac{96}{200} = \frac{0.96}{2} = 0.48 \\ \\ \frac{96}{200} \times 100 = \frac{96}{2} = 48\% \)
aerobic dancing study: a researcher wants to know which exercise program is more effective in reducing body mass index (bmi) in 60 to 70 year-old individuals with diabetes: 1) a 20 minute aerobic dancing program or 2) a 20 minute walking program. the participants in the research project will be 60 volunteers living in a large gated retirement community. participants will be randomly assigned to either the aerobic dancing group or the walking group. participants will exercise for 20 minutes a day three days a week for six months. participants will have height and weight measurements taken (in order to calculate bmi) before and after this six-month program. changes in bmi between the two groups will be compared. in the aerobic dancing study, which is the dependent variable?
Answers
As per the BMI, the dependent variable is outcome
In this study, the researcher wants to compare the effectiveness of two different exercise programs in reducing BMI in individuals with diabetes. The participants will be randomly assigned to either the aerobic dancing group or the walking group, and their BMI will be measured before and after the six-month exercise program.
The changes in BMI between the two groups will be compared to determine which exercise program is more effective in reducing BMI in this population. The dependent variable in this study is the change in BMI, as it is the outcome that is being measured and compared between the two groups.
Overall, this study will provide valuable insights into the effectiveness of different exercise programs in reducing BMI in older adults with diabetes, which can have important implications for their overall health and wellbeing.
To know more about BMI here
https://brainly.com/question/18697844
#SPJ4
7
Where would the graph of 7 appear on a number line?
O between 4 and 7
O between 1 and 2
O to the right of 11
O between 2 and 3

Answers
Answer:
between 1 and 2.
Step-by-step explanation:
The issubset() method can be used to determine whether set1 is a subset of set2. Group of answer choices. True. False.
Answers
This will return `True`, since all the elements in `set1` are also present in `set2`.
How can we explain it?True.
The `issubset()` method in Python can be used to determine if a set is a subset of another set. It returns `True` if all the elements of the first set are also present in the second set, and `False` otherwise.
For example, if we have two sets `set1 = {1, 2, 3}` and `set2 = {1, 2, 3, 4, 5}`, we can use the `issubset()` method to check if `set1` is a subset of `set2` as follows:
```
set1.issubset(set2)
```
This will return `True`, since all the elements in `set1` are also present in `set2`.
Learn more about elements
brainly.com/question/30858299
#SPJ11
I need help very quickly please, i will give brainliest! |120-x| if x<120
Answers
The |120-x| simplifies to 120-x when x is less than 120.
S If x is less than 120, then the expression |120-x| simplifies to 120-x. This is because the absolute value bars mean that the result must be positive,
so if x is already less than 120, then subtracting x from 120 will give a positive result.
For example, if x is 115, then |120-x| would equal |120-115|, which simplifies to |5|, which equals 5.
To learn more about : simplifies
https://brainly.com/question/723406
#SPJ11
a 3x3x3 cube is made of 27 small cubes of which one is blue and 26 are white. the surface of the cube is formed by 3x3 squares. the small cubes are arranged in such a way that the surface is as much white as possible. what fraction of the surface of the cube is white
Answers
The fraction of the surface of the cube which is white is 14/27
Given 27 cubes of 1 centimetre are conjoined to form a large cube of 3x3x3
To maximise the value of the surface area, in this case, taken as white, other than the cube in the centre, the rest of the cubes must have their white surface area exposed.
• Total Number of cubes where white surface area is exposed is = 27 – 1 = 26
Although, on each surface of the 3x3x3 cube, there are 9 smaller cube surfaces, and there will be a total of 6 surfaces for the bigger cube.
• Total number of cube surfaces exposed in blue = 9 * 6 = 54
• Therefore, the greatest fraction in blue= 26/54 = 13/27
Therefore the fraction of the surface of the cube is white is = 1-\(\frac{13}{27}\)= 14/27
The fraction of the surface of the cube which is white is 14/27 is the answer
To learn more about cubes, tap here:
brainly.com/question/25338305
#SPJ4
The fraction of the surface area of the cube which is white is 14/27
Given 27 cubes of 1 centimetre are conjoined to form a large cube of 3x3x3
To maximise the value of the surface area, in this case, taken as white, other than the cube in the centre, the rest of the cubes must have their white surface area exposed.
• Total Number of cubes where white surface area is exposed is = 27 – 1 = 26
Although, on each surface of the 3x3x3 cube, there are 9 smaller cube surfaces, and there will be a total of 6 surfaces for the bigger cube.
• Total number of cube surfaces exposed in blue = 9 * 6 = 54
• Therefore, the greatest fraction in blue= 26/54 = 13/27
Therefore the fraction of the surface of the cube is white is = 1-(13/27)
= 14/27
The fraction of the surface of the cube which is white is 14/27 is the answer.
To learn more about cubes, tap here:
brainly.com/question/25338305
#SPJ4
A square pyramid has a slant height of 18cm and a lateral area of 216.find the total surface area
Answers
Answer:
Step-by-step explanation:
d mkdm .,
Laura and Rich have been approved for a $325,000, 15-year mortgage with an APR of 5.3%. Using the mortgage and interest formulas, complete the two-month amortization table.
Answers
First, let's calculate the monthly interest rate (i), which is the APR divided by 12 months:
i = APR / 12 months
i = 5.3% / 12
i = 0.00442 or 0.442%
Next, let's calculate the number of months (n) for the mortgage, which is 15 years multiplied by 12 months:
n = 15 years x 12 months/year
n = 180 months
Now, let's calculate the monthly payment (PMT) using the following formula:
PMT = P * i / \((1 - (1 + i)^(-n)\))
where P is the principal amount, i is the monthly interest rate, and n is the number of months.
PMT = $325,000 * 0.00442 / (1 - \((1 + 0.00442)^(-180)\)
PMT = $2,613.67 (rounded to the nearest cent)
Now, let's create the amortization table for the first two months:
Month | Payment | Interest | Principal | Remaining Balance
1 | $2,613.67 | $1,431.25 | $1,182.42 | $323,817.58
2 | $2,613.67 | $1,428.60 | $1,185.07 | $322,632.51
For each month, the Payment column shows the fixed monthly payment, the Interest column shows the calculated interest based on the remaining balance multiplied by the monthly interest rate, the Principal column shows the portion of the payment that goes towards reducing the principal, and the Remaining Balance column shows the remaining balance after subtracting the principal payment from the previous remaining balance.
The amortization table will continue in this manner for the remaining months until the mortgage is paid off.
Learn more about “ monthly interest rate “ visit here;
https://brainly.com/question/11916359
#SPJ4
The interest and principal amounts for the first payment are:
Interest = $325,000 * 0.0044167 = $1,426.25
Principal = $2,549.67 - $1,426.25 = $1,123.42
Balance = $325,000 - $1,123.42 = $323,876.58
For the second payment, we start with the new balance of $323,876.58 and apply the formulas again:
Interest = $323,876.58 * 0.0044167 = $1,420.47
Principal = $2,549.67 - $1,420.47 = $1,129.20
Balance = $323,876.58 - $1,129.20 = $322,747.38
To complete the two-month amortization table, we need to calculate the monthly payment, as well as the principal and interest amounts for each payment.
The formula for calculating a fixed-rate mortgage payment is:
\(Payment = P * r * (1 + r)^n / [(1 + r)^n - 1]\)
Where:
P = Principal amount borrowed
r = Monthly interest rate
n = Total number of payments
First, let's calculate the monthly interest rate.
Since the APR is an annual rate, we need to divide it by 12 to get the monthly rate:
Monthly interest rate = 5.3% / 12 = 0.0044167
Next, we need to calculate the total number of payments.
Since this is a 15-year mortgage, and we're completing a two-month amortization table, the total number of payments is:
Total number of payments = 15 years * 12 months per year = 180
Number of payments for two months = 2
Now we can plug these values into the formula to calculate the monthly payment:
Payment = \($325,000 * 0.0044167 * (1 + 0.0044167)^180 / [(1 + 0.0044167)^180 - 1]\)
= $2,549.67
So the monthly payment is $2,549.67
Now we can use this value to complete the two-month amortization table:
Payment Interest Principal Balance
Month 1 $1,426.25 $1,123.42 $323,876.58
Month 2 $1,420.47 $1,129.20 $322,747.38
To calculate the interest and principal amounts for each payment, we use the following formulas:
Interest = Balance * Monthly interest rate
Principal = Payment - Interest
Balance = Balance - Principal
We start with the initial balance of $325,000 and apply the formulas for each payment.
The interest and principal amounts for the first payment are:
Interest = $325,000 * 0.0044167 = $1,426.25
Principal = $2,549.67 - $1,426.25 = $1,123.42
Balance = $325,000 - $1,123.42 = $323,876.58
For the second payment, we start with the new balance of $323,876.58 and apply the formulas again:
Interest = $323,876.58 * 0.0044167 = $1,420.47
Principal = $2,549.67 - $1,420.47 = $1,129.20
Balance = $323,876.58 - $1,129.20 = $322,747.38
And so on, for each subsequent payment.
For similar question on amortization.
https://brainly.com/question/29485954
#SPJ11
College Algebra Applied Problem Four A medical professional is helping an individual balance their diet. The individual has asked for some certain foods to remain in their diet. They will always get 600 calories from carbohydrates. The individual says that they can be flexible about how many calories they consume in fats and proteins. The goal of the diet is to keep the individual at 1,800 calories per day ( 600 of which come from carbohydrates). Part One Write an equation that models the amount of calories from fats " f ' and protein "p" that the individual can consume in order to reach 1,800 calories. Part Two The diet being prescribed to the individual calls for calories from protein to be three times the calories from fat. Write an equation based on this information that relates calories from protein "p" to calories from fat " f ". Part Three Use your equations from parts "b" and "c" to solve this system of equations and determine the amount of calories that the individual should consume from fats and proteins. Part Four If the individual no longer required 600 calories from carbohydrates, and instead said that they would be flexible about how many carbohydrates they would consume, how many variables would there be for this problem on calories?
Answers
The system equation that models the amount of calories from fats (f) and proteins (p) that the individual can consume to reach 1,800 calories is: f + p = 1,200. The equation that relates calories from protein (p) to calories from fat (f) based on the prescribed diet is: p = 3f. Solving the system of equations, we find that the individual should consume 300 calories from fats and 900 calories from proteins.
To find the equation that models the amount of calories from fats and proteins that the individual can consume in order to reach 1,800 calories, we consider that 600 calories will come from carbohydrates. Since the total goal is 1,800 calories, the remaining calories from fats and proteins should add up to 1,800 - 600 = 1,200 calories. Therefore, the equation is f + p = 1,200.
Based on the prescribed diet, the individual is required to consume calories from protein that are three times the calories from fat. This relationship can be expressed as p = 3f, where p represents the calories from protein and f represents the calories from fat.
To solve the system of equations, we substitute the value of p from the second equation into the first equation: f + 3f = 1,200. Combining like terms, we get 4f = 1,200, and dividing both sides by 4 yields f = 300. Substituting this value back into the second equation, we find p = 3(300) = 900.
Therefore, the individual should consume 300 calories from fats and 900 calories from proteins to meet the diet requirements and achieve a total of 1,800 calories.
Learn more about system equation
brainly.com/question/32645146
#SPJ11
Determine if the statement is TRUE or FALSE. Justify your answer. a) Given matrix , and are orthogonal complements. b) If is an orthogonal matrix, then .
Answers
The statement in part b) is TRUE. If Q is an Orthogonal matrix, then Q^-1 is equal to its transpose, Q^T.
a) The statement "Given matrix A, A⊥ and A⊥⊥ are orthogonal complements" is FALSE.
To understand why, we need to define the terms "orthogonal complement" and "orthogonal matrix."
In linear algebra, the orthogonal complement of a subspace is the set of all vectors that are orthogonal (perpendicular) to every vector in that subspace. If we have a subspace A, its orthogonal complement is denoted by A⊥.
Now, the orthogonal complement of A⊥ is denoted as A⊥⊥. It consists of all vectors that are orthogonal to every vector in A⊥.
In general, it is not true that A⊥ and A⊥⊥ are orthogonal complements. A⊥⊥ is the subspace that contains all vectors orthogonal to the vectors in A⊥, not the original subspace A.
b) The statement "If Q is an orthogonal matrix, then Q^-1 = Q^T" is TRUE.
An orthogonal matrix is a square matrix in which the columns are mutually orthogonal unit vectors (orthonormal). The inverse of an orthogonal matrix is equal to its transpose.
By definition, if Q is an orthogonal matrix, then Q^T is the transpose of Q. The transpose of a matrix swaps its rows and columns.
When we take the inverse of an orthogonal matrix, Q^(-1), it is equivalent to Q^T. Therefore, Q^-1 = Q^T for an orthogonal matrix.
This property holds true for orthogonal matrices and is an important characteristic of these matrices. It ensures that the product of a matrix and its transpose (or inverse) preserves the orthogonality of the vectors in the matrix.
In summary, the statement in part b) is TRUE. If Q is an orthogonal matrix, then Q^-1 is equal to its transpose, Q^T. However, the statement in part a) is FALSE. A⊥ and A⊥⊥ are not orthogonal complements.
For more questions on Orthogonal .
https://brainly.com/question/28453791
#SPJ8
Given the definitions of f(x) and g(x) below, find the value of f(g(0)).
f(x) = 2x² − 5x + 12
g(x) = -3x - 3
Answers
Answer:
f(g(0)) = 45
Step-by-step explanation:
to evaluate f(g(0)) , evaluate g(0) then substitute the value obtained into f(x)
g(0) = - 3(0) - 3 = 0 - 3 = - 3 , then
f(- 3) = 2(- 3)² - 5(- 3) + 12
= 2(9) + 15 + 12
= 18 + 27
= 45
PLEASE HELP! THANKS!!

Answers
Answer:
\( = 10 {x}^{2} - 4x\)
Step-by-step explanation:
\(2x(5x - 2)\)
\( = 10 {x}^{2} - 4x\)
=(2x*5x)-(2x*-2)
=10x^2-4x