John and Dawn have been married for over 20 years. They have lived in their home in Northville, MI (a suburb of Detroit) with their three children for most of those years. According to the Census Bureau, which type of household do they live in
Answers
It is most likely that John and Dawn live in a "married couple with children" household. They have been married for over 20 years and have three children residing with them in their home in Northville, MI.
John and Dawn have been married for over 20 years and have lived in their home in Northville, MI with their three children for most of those years. To determine the type of household they live in, we can consider the various household classifications provided by the Census Bureau.
Married couple with children: This classification applies to households where a married couple resides with one or more children who are under the age of 18. Since John and Dawn have three children, it is possible that they fall under this category.
Married couple without children: This classification includes households where a married couple resides without any children under the age of 18. However, since John and Dawn have three children, this classification is not applicable to their situation.
Single-parent household: This classification applies when a single parent resides with one or more children under the age of 18. Since John and Dawn are married, this classification is not relevant in their case.
Other household types: There are several other household types defined by the Census Bureau, such as multi-generational households, unmarried partner households, and non-family households. However, based on the given information, none of these classifications seem to apply to John and Dawn's situation.
Considering the information provided, it is most likely that John and Dawn live in a "married couple with children" household. They have been married for over 20 years and have three children residing with them in their home in Northville, MI.
for such more question on residing
https://brainly.com/question/20492463
#SPJ11
Related Questions
.Given a term in an arithmetic sequence and the common difference find the first five terms.
1.a1=28, d=10
2.a1=-34, d=-10
3.a1=35, d=4
4.a1=2, d=3k
5.a1=1/6, d=1/2
Answers
The first five terms of the arithmetic sequence with a1 = 28 and d = 10 are 28, 38, 48, 58, and 68. The first five terms of the arithmetic sequence with a1 = -34 and d = -10 are -34, -44, -54, -64, and -74.
The first five terms of the arithmetic sequence with a1 = 35 and d = 4 are 35, 39, 43, 47, 51.The first five terms of the arithmetic sequence with a1 = 2 and d = 3k are: 2, 2 + 3k, 2 + 6k, 2 + 9k, 2 + 12k.The first five terms of the arithmetic sequence with a1 = 1/6 and d = 1/2 are: 1/6, 1/6 + 1/2, 1/6 + 1, 1/6 + 3/2, 1/6 + 2.
To find the first five terms of an arithmetic sequence, we start with the given first term (a1) and add the common difference (d) successively to obtain the subsequent terms. In each case, we use the given values of a1 and d to calculate the corresponding terms by adding the appropriate multiples of d to a1.
The resulting sequence of terms represents the arithmetic sequence. By applying this process to each given scenario, we obtain the first five terms for each arithmetic sequence as listed above.
Learn more about arithmetic sequence here: brainly.com/question/28882428
#SPJ11
Brayden bought a helium tank for $24. It will blow up 30 balloons. Write an equation relating the total cost y to the number of balloons x.
Answers
The equation relating the total cost (y) to the number of balloons (x) is y = 0.8x.
We are given the following information:
1. The cost of the helium tank is $24.
2. The tank can inflate 30 balloons.
We need to write an equation relating the total cost (y) to the number of balloons (x).
Since the helium tank cost is a fixed amount, we can divide this cost by the number of balloons it can inflate to find the cost per balloon.
Cost per balloon = Total cost of the tank / Number of balloons
Cost per balloon = $24 / 30
Now, we can write the equation relating y and x as follows:
y = (Cost per balloon) * x
Plug in the value for the cost per balloon calculated above:
y = ($24/30) * x
Simplify the equation:
y = $0.8 * x
So, the equation relating the total cost (y) to the number of balloons (x) is:
y = 0.8x
This equation shows that the total cost (y) is equal to the cost per balloon ($0.8) multiplied by the number of balloons (x). It helps us calculate the total cost for inflating any number of balloons using the helium tank.
For more about equation:
https://brainly.com/question/10413253
#SPJ4
where is the center of the face of the cube?
Answers
The center of the face of a cube is the midpoint of the face and lies along the line that runs between the opposite vertices of the face.
Where is the center of the face of a cube?This is the point of intersection of the two diagonals in a face. In other words, it is the point that is equidistant from all four corners of the face.
To visualize this, imagine dividing the face into four equal triangles by drawing lines from each corner to the center. The center of the face is at the intersection of these lines.
In three-dimensional space, the center of the face of a cube is also the center of the cube itself, as all faces of a cube are congruent (the same shape and size) and meet at the center of the cube.
Learn more about center of a cube at:
https://brainly.com/question/17437097
#SPJ1
a process used to manufacture paint yields, on the average, 70 tons of paint each day. yields, however , vary from day to day due to changes in raw materials and plant conditions. suppose, it is established that the daily yields are normally distributed, and that the variability from one day to the other is more or less independent , and the standard deviation is 3 tons. because of increasing demand for this type of paint, certain modifications are suggested , and we are interested in estimating the mean yield of this modified process. how many sample observations do we have to obtain if we want to be 98% confident that our estimate is within 1 ton of the true, but unknown mean?
Answers
Using the Sample size formula , the sample manufactuer of paints observations or sample size is 22 ton .
Sample size: It is defined as the number of participants or total observations in a study of sample.
we have provided that,
standard deviations of sample (σ)= 3 tons
mean of sample ( X) = 70 tons
confidence level = 98% = 0.98
Margin of error (M.E) = 1 ton
Using the sample size formula,
n = z²(σ)(1-σ) /( M.E)²[1+σ (1-σ)z²/(M.E)²X]
where, X---> population size
s.d --> standard deviations
M.E ---> margin of error
Z-value for confidence level
so, z-value corresponding to 98% of confidence level is 2.32 ..
putting all the values in above formula we get, n = (2.32)²(2)3/(1)²(1+ (2.32)²(6)70×1)
=> n= 32.29/(1+(0.46))= 32.29/ 0.46
= 22.1 ~ 22
Hence, sample size is 22 ton .
To learn more about sample size, refer:
ttps://brainly.com/question/24158610
#SPJ4
Find a Cartesian equation for the curve.r^2 cos(2θ) = 36
Answers
The equation of the given curve is given by r2 cos(2θ) = 36.
To find the Cartesian equation of the curve, we need to convert the polar equation into its equivalent Cartesian form. This can be done by substituting x = r cos θ and y = r sin θ into the given equation, yielding:
x2cos(2θ) + y2cos(2θ) - 36 = 0
Using the identity cos(2θ) = cos2θ - sin2θ, the equation can be rewritten as:
x2(cos2θ - sin2θ) + y2(cos2θ - sin2θ) - 36 = 0
Simplifying, we get:
x2 - y2 - 36 = 0
To know more about Cartesian equation refer here:
https://brainly.com/question/27927590
#SPJ11
Driving under the influence of alcohol (DUI) is a serious offense. The following data give the ages of a random sample of 50 drivers arrested while driving under the influence of alcohol. This distribution is based on the age distribution of DUI arrests given in the Statistical Abstract of the United States (112th Edition). 46 16 41 26 22 33 30 22 36 34 63 21 26 18 27 24 31 38 26 55 31 47 27 43 35 22 64 40 58 20 49 37 53 25 29 32 23 49 39 40 24 56 30 51 21 45 27 34 47 35 (a) Make a stem-and-leaf display of the age distribution. (Use the tens digit as the stem and the ones digit as the leaf. Enter numbers from smallest to largest separated by spaces. Enter NONE for stems with no values. )
Answers
To make a stem-and-leaf display, we will separate the ages into stems based on the tens digit and leaves based on the ones digit.
Therefore, the stem-and-leaf display of the age distribution is:
1 | 6
2 | 6 8 9
3 | 3 7 8
4 | 1 3 6 7 8 9
5 | 3 5
6 | 3 4 5 8
A stem-and-leaf display is a graphical representation of a set of data. It is a way to organize and display data in a way that allows for easy interpretation and comparison of the data.
In a stem-and-leaf display, the data is separated into two parts: the stem and the leaf. The stem represents the tens digit of each data point, and the leaf represents the ones digit. For example, the number 47 would be represented as a stem of 4 and a leaf of 7.
The stems are listed vertically, and the leaves are listed horizontally next to their respective stems. The leaves are usually listed in increasing order.
Learn more about Standard Distribution here:
https://brainly.com/question/27275125
#SPJ4
Consider the curve x³y + y³ = sin y - x². Find dy/dx
Answers
Considering the curve x³y + y³ = sin y - x, the final i is;\(\frac{dy}{dx} = \frac{-2x}{3y^2 - cos(y)} \div (x^3 - cos(y))\)
Implicit differentiation is a technique used to differentiate equations that are not explicitly expressed in terms of one variable. It is particularly useful when you have an equation that defines a relationship between two or more variables, and you want to find the derivatives of those variables with respect to each other.
To find dy/dx for the curve x³y + y³ = sin y - x², the implicit differentiation will be used which involves differentiating both sides of the equation with respect to x.
It is expressed as follows;
\(\frac{d}{dx} x^3y + \frac{d}{dx} y^3 = \frac{d}{dx} sin(y) - \frac{d}{dx} x^2\)
Then we'll differentiate each term:
For the first term, x^3y, we'll use the product rule
\(\frac{d}{dx} x^3y = 3x^2y + x^3 \frac{dy}{dx}\)
For the second term, y^3, we'll also use the chain rule
\(\frac{d}{dx} y^3 = 3y^2 \frac{dy}{dx}\)
For the third term, sin(y), we'll again use the chain rule
\(\frac{d}{dx} sin(y) = cos(y) \frac{dy}{dx}\)
For the fourth term, x², we'll use the power rule
\(\frac{d}{dx} x^2 = 2x\)
Substituting these expressions back into the original equation, we get:
3x²y + x³(dy/dx) + 3y²(dy/dx) = cos(y)(dy/dx) - 2x
Simplifying the equation:3x²y + x³(dy/dx) + 3y²(dy/dx) - cos(y)(dy/dx) = -2x
Dividing both sides by 3y² - cos(y), we get:(x³ - cos(y))(dy/dx) = -2x / (3y² - cos(y))
Hence, the final answer is;\(\frac{dy}{dx} = \frac{-2x}{3y^2 - cos(y)} \div (x^3 - cos(y))\)
To know more about implicit differentiation, visit:
https://brainly.com/question/11887805
#SPJ11
a square has 2x+3. if a rectangles made up of three of these squares , which expression would represent the perimeter of the rectangle ?
Answers
Answer:
The perimeter of the rectangle that contains the 3 squares is 24x + 36 units
Step-by-step explanation:
Here, we have a square with side length 2x + 3
The perimeter of this square would be calculated using the mathematical formula;
P = 4L
P = 4(2x + 3) = 8x + 12 units
Now, this particular rectangle is composed of three of these squares.
The expression which would represent the perimeter of the rectangle is equal to the sum of the perimeters of the 3 squares.
That would be 8x + 12 + 8x + 12 + 8x + 12 or simply 3(8x + 12) = 24x + 36
How many cups of water will Billy use to fill a 9-liter bucket if one cup holds of a liter of water
Answers
Answer:
9 cups!
Step-by-step explanation:
I cup = 1 liter
? cups = 9 liter
1 * 9 = 9
so ? * 1 = 9
? = 9
Answer:
The answer is
Step-by-step explanation:
59 cups
sry if im wrong
Help me with this, it’s due in a bit!

Answers
Answer:
64 square centimeters
Step-by-step explanation:
The surface are of a pyramid is found by finding the sum of the area of the four sides and the base.
Finding the triangular face:
Area of triangle = \(\frac{1}{2} b h\) = \(\frac{1}{2}*4*6 = 12\)
12 * 4 (4 sides) = 48 square cm
Finding the Base = \(w * l = 4 * 4 = 16\)
Finally, we add it together. 48 + 16 = 64
What are the endpoint coordinates for the midsegment of △BCD that is parallel to BC¯¯¯¯¯?
Enter your answer, as a decimal or whole number, in the boxes.
( , ) and ( , )

Answers
Answer:
(3,3) (-1,-3), you just have to look at the coordinates
Please help!!! Look at image. Excuse my answers I’m not sure if there right.

Answers
Quotient: 6x+2
Remainder: 20/x^2+3 (20 over x to the power of 2 plus 3)
18-
Quotient: x^2+3 (x to the power of 2 plus 3)
Remainder: 6/4x^2+2 (6 over 4 x to the power of 2 plus 2)

can someone help please
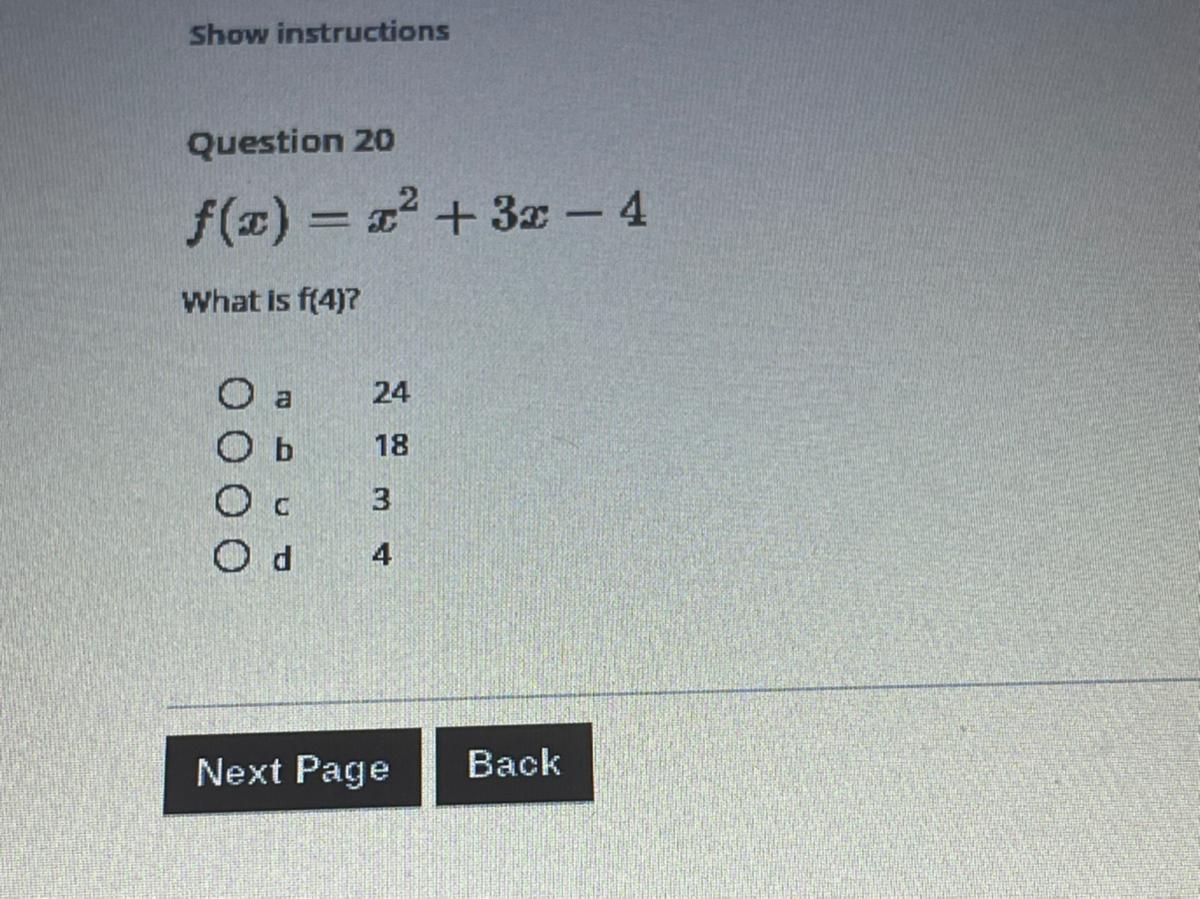
Answers
Answer:
isn't it b i remember doing something almost the same as this
Answer:
24
Step-by-step explanation:
f(4) means you plug the 4 into the equation so 4 x 4= 16
then 3(4)= 12
16+12-4=24
9000 invested at 8% compounded annually. In how many years will
the account have grown to $14500
Answers
It will take approximately 6.2 years for the account to grow to $14500 when $9000 is invested at 8% interest compounded annually.
What is the time needed to acquire the accrued amount?The compound interest formula is expressed as:
\(A = P( 1 + \frac{r}{t})^{nt}\)
\(t = \frac{In(\frac{A}{P} )}{n[In(1 + \frac{r}{n} )]}\)
Where A is accrued amount, P is the principal, r is the interest rate and t is time.
Given that:
Principal P = $9,000, compounded annually n = 1, interest rate r = 8%, Accrued amount A = $14500.
Plug these values into the above formula and solve for time t.
\(t = \frac{In(\frac{A}{P} )}{n[In(1 + \frac{r}{n} )]}\\\\t = \frac{In(\frac{14,500}{9,000} )}{1*[In(1 + \frac{0.08}{1} )]}\\\\t = \frac{In(\frac{14,500}{9,000} )}{[In(1 + 0.8 )]}\\\\t = \frac{In(\frac{14,500}{9,000} )}{[In(1.8 )]}\\\\t = 6.197 \ years\)
Therefore, the time required is 6.197 years.
Learn more about compound interest here: brainly.com/question/27128740
#SPJ1
which of the following is a probability sample?
a. Quota sample
b. Convenience sample
c. Cluster sample
d. Judgment sample
e. Snowball sample
Answers
The correct option is option (C) .
Cluster Sampling is a type of probability sampling and other options are non- probability sampling examples .
Sampling :
Sampling is defined as a technique that selects individual members or subsets from a population to help determine characteristics of the population as a whole.
Croach and Housden postulate that a sample is a finite number taken from a large group for testing and analysis, and that the sample can be taken as representative of the group as a whole.
There are two main types of sampling:
i) probability sampling
ii) Non-probability sampling
A) probability sampling:
It is defined as the sampling technique which researchers use a related method to draw probability theory samples from a larger population.
The most important requirement for probabilistic sampling is that everyone in the population has a known equal chance of being selected.
Probability Samples:
1. Stratified Sampling: Stratified sampling is a type of sampling technique that divides the total population into smaller groups or strata to complete the sampling process. Hierarchies are formed based on some common characteristics of demographic data.
2. Cluster Sampling: Cluster sampling is a probabilistic sampling technique in which researchers divide a population into multiple groups (clusters) for research purposes. Researchers then select random groups using simple sampling techniques for data collection and data analysis.
To learn more about Probability sample, refer:
https://brainly.com/question/29313175
#SPJ4
help please will give brainliest no question

Answers
Answer:
The penguins swan 2 2/5 miles in one hour
Step-by-step explanation:

NEW Conditional:
If it is raining, then it is spring.
Bill claims this conditional is not true,
can you write a counterexample for Bill?
Answers
what is 4.414*10’9 in standard form
Answers
Answer:
4,414,000,000
Step-by-step explanation:
4.414x10^9, move the decimal place 9 places to the left.
Answer:
4,414,000,000
Step-by-step explanation:
4.414 x 10⁹
= 4.414 x 1,000,000,000
= 4,414,000,000
What is the slope for y=200-5x
Answers
Answer:
5
Step-by-step explanation:
The slope is 5 because the equation is y = 200-5x where 5 is the slope because it is the rate of change.
y = -5x + 200
y = -5x + 200; m = -5
What’s the diameter of a circle that had a radius of 4cm
Answers
Answer:
8
Step-by-step explanation:
Answer is =8cm
Step-by-step explanation:
d=2r=2·4=8cm
Xavier performs the elementary row operation represented by Ri - R, on matrix A.
Answers
The elementary row operation \(R_i - R_j\) can be used to manipulate the rows of a matrix and is a fundamental tool in the process of row reduction (also known as Gaussian elimination) for solving systems of linear equations and computing matrix inverses.
A matrix is a rectangular array of numbers or other mathematical objects arranged in rows and columns. Matrices are used in many areas of mathematics, as well as in physics, engineering, and computer science. The dimensions of a matrix are given by the number of rows and columns it contains. For example, a matrix with three rows and two columns is called a 3x2 matrix.
The entries of a matrix can be any mathematical object, but they are usually real or complex numbers. Matrices can be added and multiplied, which leads to many useful operations and applications. Matrix addition and multiplication are defined element-wise, meaning that the corresponding entries of two matrices are added or multiplied. Matrices can also be used to represent transformations of geometric objects, such as rotations, translations, and scaling.
To learn more about Matrix visit here:
brainly.com/question/28180105
#SPJ4
Complete Question:
Xavier performs the elementary row operation represented by Ri - R, on matrix A.
A pyramid has a base that is a right triangle with legs measuring 10 cm and 14 cm. The height of the pyramid is 9 cm.
The volume of the pyramid is ___ cubic cm.
Answers
Explanation: Equation to find a pyramid is l x w x h / 3, so you multiply the length, width, and height to get 1260. Divide that by 3, and you get 420.
Joshua Murphy is planning on studying late into the night for his economics exam. How many cups of coffee should he buy tonight
Answers
Joshua should continue continue buying the coffee until the marginal benefit equals to the marginal cost.
What is marginal benefit?The marginal benefit simply means the maximum amount that a consumer is willing to pay for an additional good or service.
From the complete information, Joshua should keep buying coffee through the evening until the marginal benefit of purchasing one more coffee equals the marginal cost.
Learn more about marginal benefit on:
https://brainly.com/question/11937697
Enter the equation in standard form.
y = 4x − 2
Answers
Answer:
y-4x=-2
Step-by-step explanation:
standard form is just putting both variables on the same side.
hope this helps :)
sequoia can wash six dishes every two minutes. how long will it take her to wash a stack of 60 dishes?
Answers
If you divide 6/2, thats 3 dishes every minute. 60/3= 20 minutes to wash 60 dishes
Find the value of x. A. 0 B. 3 C.4 D. 12.

Answers
Answer:
B = 3
Step-by-step explanation:
3x + 15 = 4x + 12
= 15-12=4x-3x
= 3 = x
X = 3
An angle that measures from the horizontal upward to an object is called the angle of ________, whereas an angle that measures from the horizontal downward to an object is called the angle of ________.
Answers
An angle that measures from the horizontal upward to an object is called the angle of elevation, whereas an angle that measures from the horizontal downward to an object is called the angle of depression.
The angle of elevation is commonly used in surveying, navigation, and construction to determine the height of objects, such as buildings, towers, and mountains.
To find the height of an object using the angle of elevation, one needs to measure the distance between the observer and the object and the angle between the horizontal and the line of sight from the observer to the top of the object. By applying trigonometry, one can then calculate the height of the object.
On the other hand, the angle of depression is often used to measure the depth of objects, such as wells, valleys, and caves.
To find the depth of an object using the angle of depression, one needs to measure the distance between the observer and the object and the angle between the horizontal and the line of sight from the observer to the bottom of the object. Again, by applying trigonometry, one can then calculate the depth of the object.
To learn more about angle click on,
https://brainly.com/question/20352216
#SPJ4
The integral of [(x^2)(y^2)dx + x y dy] where C consists of the arc of the parabola y = x^2 from (0,0) to (1,1) and the line segments from (1,1) to (0,1) using line integral and Green theorem please
Answers
The line integral ∫[C] (Pdx + Qdy) over the given curve C consisting of the arc of the parabola y = x² from (0,0) to (1, 1), and the line segment from (1,1) to (0,1) is equal to 2/5.
What is integral?
The value obtained after integrating or adding the terms of a function that is divided into an infinite number of terms is generally referred to as an integral value.
To evaluate the line integral using Green's theorem, we need to find a vector field F = (P, Q) such that ∇ × F = Qₓ - Pᵧ, where Qₓ represents the partial derivative of Q with respect to x, and Pᵧ represents the partial derivative of P with respect to y.
Let's consider F = (P, Q) = (x²y², xy).
Now, let's calculate the partial derivatives:
Qₓ = ∂Q/∂x = ∂(xy)/∂x = y
Pᵧ = ∂P/∂y = ∂(x²y²)/∂y = 2x²y
The curl of F is given by ∇ × F = Qₓ - Pᵧ = y - 2x²y = (1 - 2x²)y.
Now, let's find the line integral using Green's theorem:
∫[C] (Pdx + Qdy) = ∫∫[R] (1 - 2x²)y dA,
where [R] represents the region enclosed by the curve C.
To evaluate the line integral, we need to parameterize the curve C.
The arc of the parabola y = x² from (0, 0) to (1, 1) can be parameterized as r(t) = (t, t²) for t ∈ [0, 1].
The line segment from (1, 1) to (0, 1) can be parameterized as r(t) = (1 - t, 1) for t ∈ [0, 1].
Using these parameterizations, the region R is bounded by the curves r(t) = (t, t²) and r(t) = (1 - t, 1).
Now, let's calculate the line integral:
∫∫[R] (1 - 2x²)y dA = ∫[0,1] ∫[t²,1] (1 - 2t²)y dy dx + ∫[0,1] ∫[0,t²] (1 - 2t²)y dy dx.
Integrating with respect to y first:
∫[0,1] [(1 - 2t²)(1 - t²) - (1 - 2t²)t²] dt.
Simplifying:
∫[0,1] [1 - 3t² + 2t⁴] dt.
Integrating with respect to t:
[t - t³ + (2/5)t⁵]_[0,1] = 1 - 1 + (2/5) = 2/5.
Therefore, the line integral ∫[C] (Pdx + Qdy) over the given curve C consisting of the arc of the parabola y = x² from (0,0) to (1,1), and the line segment from (1,1) to (0,1) is equal to 2/5.
To learn more about the integration visit:
brainly.com/question/30094386
#SPJ4
If a 98% confidence interval has bounds 73 and 80, which of the following could be the bounds for a 95% confidence interval? A. 73 and 81. B. 72 and 79. C. 72 and 81. D. 74 and 79.
Answers
The bounds for a 95% confidence interval could be option (B) 72 and 79
We know that the 98% confidence interval has bounds of 73 and 80. This means that if we were to repeat the same experiment many times, we would expect that 98% of the time, the true population mean would fall within this range.
To find the bounds for a 95% confidence interval, we can use the fact that a higher confidence level corresponds to a wider interval, and a lower confidence level corresponds to a narrower interval.
Since we want a narrower interval for a 95% confidence level, we can expect the bounds to be closer to the sample mean. We can calculate the sample mean as the midpoint of the 98% confidence interval
(sample mean) = (lower bound + upper bound) / 2 = (73 + 80) / 2 = 76.5
Next, we can use the formula for a confidence interval:
(sample mean) ± (z-score) × (standard error)
where the z-score depends on the desired confidence level, and the standard error depends on the sample size and sample standard deviation. Since we don't have this information, we can assume that the sample size is large enough (i.e., greater than 30) for the central limit theorem to apply, and we can use the formula
standard error = (width of 98% CI) / (2 × z-score)
For a 98% confidence interval, the z-score is 2.33 (found using a standard normal distribution table or calculator). Plugging in the values, we get
standard error = (80 - 73) / (2 × 2.33) = 1.70
Now, we can use this standard error to calculate the bounds for a 95% confidence interval
(sample mean) ± (z-score) × (standard error) = 76.5 ± 1.96 × 1.70
Simplifying, we get
(lower bound) = 76.5 - 3.33 = 73.17
(upper bound) = 76.5 + 3.33 = 79.83
Therefore, the correct option is (B) 72 and 79
Learn more about confidence interval here
brainly.com/question/24131141
#SPJ4
Lauren is given a 12% pay rise.Her new salary is £24,080. What was Lauren's salary before the pay rise?
Answers
Answer:
The base salary was £21,500.
Step-by-step explanation:
Giving the following information:
Increase rate (g)= 12%
New salary= £24,080
To calculate the base salary, we need to use the following formula:
Base salary= new salary / (1 + increase rate)
Base salary= 24,080 / (1.12)
Base salary= £21,500
The base salary was £21,500.