Jocelyn's car tires are spinning at a rate of 120 revolutions per


minute. If her car's tires are 28 inches in diameter, how many


miles does she travel in 5 minutes? Round to the nearest


hundredth. 63360 inches = 1 mile.

The answer to the question is 9±√21/2

By using the quadratic formula x=-b±√b²-4ac/2a

By comparing  x²-9 x+15=0  with ax²+bx+c

we get a=1 b=-9 c=15

x=-(-9)±√(-9)²-4×1×15/2×1

x=9±√81-60/2

x=9±√21/2

So the answer to the question is x=9+√21/2

and x=9-√21/2

Learn more about quadratic formula here:https://brainly.com/question/1214333

#SPJ4

The option B, "The adult male foot length of 23.8 cm is significantly low because it is less than 24.26 cm" is correct.

In the given question, a group of adult males has foot lengths with a mean of 26.84 cm and a standard deviation of 1.29 cm.

We have to find the adult male foot length of 23.8 cm significantly low or significantly​ high.

According to thumb rule, a value is significantly low if it is 2 standard deviations below mean and significantly high if it is 2 standard deviations above mean

Mean = 26.84 cm

Standard deviation = 1.29 cm

Significantly low value = 26.84 - 2*1.29 = 24.26 cm

Significantly high value = 26.84 + 2*1.29 = 29.42 cm

Significantly low values are 24.26 cm or lower.

Significantly high values are 29.42 cm or higher.

The adult male foot length of 23.8 is lower than the significant low value of 24.26.

So the option B, "The adult male foot length of 23.8 cm is significantly low because it is less than 24.26 cm" is correct.

To learn more about thumb rule link is here

brainly.com/question/607952

#SPJ4

Awnser:

-5,9

Step-by-step explanation:

if your looking for the roots of zeros.

Answer:

$1.70

PLEASE MARK BRAINLIEST

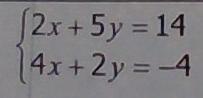
Answer:  

The answer to 52 divided by 91 calculated using Long Division is:

0

52 Remainder

Step-by-step explanation:

Answer: $3.96 per quart

Step-by-step explanation:

2 gallons = 8 quarts

Price per quart = 31.68/8 = $3.96

Therefore, price per quart = $3.96

Answer:

$3.36 per gallon

Step-by-step explanation:

So 2 gallons is equal to 8 quarts, so then you do $31.68 divided by 8 which gives you the answer of $3.36 per gallon

Answer:

\(\boxed{\underline{\tt B.\:x=-1}}\)

Step-by-step explanation:

\(\tt 8=2^{(x+4)}\)

(First, convert both sides to the same base):-

\(\tt 2^3=2^{x+4}\)

(Now, cancel the base of 2 on both sides):-

\(\tt 3=x+4\)

(Subtract 4 from both sides):-

\(x+4-4=3-4\)

\(\tt x=-1\)

~

We can see that the first component of the vector equation is always zero, so the parabola lies in the xz-plane.

Moreover, the second component is a quadratic function of t, which gives us a vertical parabola when plotted in the yz-plane. The third component is a linear function of t, so the curve extends infinitely in both directions. Therefore, we have a vertical parabola in the xz-plane.

This statement is referring to a specific vector-valued function, which we can write as:

f(t) = (0, t^2, ct)

where c is a constant.

The second component of this vector function is t^2, which is a quadratic function of t. When we plot this function in the yz-plane (i.e., we plot y = t^2 and z = 0), we get a vertical parabola that opens upward. This is because as t increases, the value of t^2 increases more and more quickly, causing the curve to curve upward.

The third component of the vector function is ct, which is a linear function of t. When we plot this function in the xz-plane (i.e., we plot x = 0 and z = ct), we get a straight line that extends infinitely in both directions. This is because as t increases or decreases, the value of ct increases or decreases proportionally, causing the line to extend infinitely in both directions.

To know more about parabola,

https://brainly.com/question/28973830

#SPJ11

Answer:

I had the same problem on imagine math too. The answer for the first part is 120=48+6p. The answer for the second one is 12 Because 12 x 6=72 + 48 = 120.

Step-by-step explanation:

Answer:

10.2π

Step-by-step explanation:

Given data

Area of circle=  81 ft^2

Also, the expression for the area of a circle is

A=πr^2

substitute

81=3.142*r^2

r^2= 81/3.142

r^2= 25.77

square both sides

r= √25.77

r= 5.1

Also, the expression for the circumference is

C= 2πr

substitute

C= 2*π*5.1

C= 10.2π

Hence the circumference is 10.2π

Answer: 5798

Step-by-step explanation:

Probability of \(1\) success as per given condition is equals to \(0.384475\) ≈ \(0.4\).

" Probability is defined as the ratio of number of favourable outcomes to the total number of outcomes.Probability is always less than or equals to one."

Formula used

For binomial experiment

Probability =  \(^n C_r p^{r} q^{n-r}\)

\(p =\)success rate

\(q=\) failure rate

\(p+q=1\)

\(n=\)Number of trials

\(r=\) number of success

According to the question,

Total number of trials \('n' =4\)

Number of success \('r' =1\)

\(p = 0.35\\\\q = 1-0.35\\ \\\implies q = 0.65\)

Substitute the value to get the required probability,

Probability \(= ^4C_1 (0.35)^{1}(0.65)^{4-1}\)

                   \(=\frac{4!}{(4-1)!1!} \times\frac{35}{100}\times(\frac{65}{100})^{3} \\\\= 4 \times \frac{35}{100}\times \frac{274625}{1000000} \\\\= 0.384475\)

                   ≈ \(0.4\)

Hence, probability of \(1\) success as per given condition is equals to \(0.384475\) ≈ \(0.4\).

Learn more about probability here

brainly.com/question/11234923

#SPJ2

To prove that f = g, we need to show that for any vector x in rn, f(x) = g(x).

We know that f and g have nonnegative eigenvalues, which means that there exist real numbers λ1, λ2, ..., λn such that:

f(x) = λ1x1v1 + λ2x2v2 + ... + λnxnv_n,

g(x) = μ1x1w1 + μ2x2w2 + ... + μnxnw_n,

where v1, v2, ..., vn and w1, w2, ..., wn are orthonormal bases of eigenvectors corresponding to the eigenvalues λ1, λ2, ..., λn and μ1, μ2, ..., μn respectively.

Since both f and g are positive semidefinite, we know that λi and μi are nonnegative for all i. We also know that f^2 = g^2, which means that (f^2 - g^2)(x) = 0 for all x in rn.

Expanding this equation using the expressions for f(x) and g(x) above, we get:

(λ1^2 - μ1^2)x1v1 + (λ2^2 - μ2^2)x2v2 + ... + (λn^2 - μn^2)xnvn = 0.

Since the vectors v1, v2, ..., vn form an orthonormal basis, we can take the inner product of both sides with each vi separately. This gives us n equations of the form:

(λi^2 - μi^2)xi = 0,

which implies that λi = μi for all i, since λi and μi are both nonnegative.

Now, since λi = μi for all i, we have:

f(x) = λ1x1v1 + λ2x2v2 + ... + λnxnv_n = μ1x1w1 + μ2x2w2 + ... + μnxnw_n = g(x),

which shows that f = g.

Learn more about numbers here

brainly.in/question/16165023

#SPJ11

1.  x² - 5x - 16 can be written as (x - 8)(x + 2).

2. 6an² - 3b²n² = n²(6a - 3b²).

3. This expression represents a perfect square trinomial, which can be factored as (2x - y)².

4. Combining like terms, we get -n³ - n² + n + 1 = -(n³ + n² - n - 1).

5. 17x³y⁴z⁶ = (x²y²z³)².

6. 12a²b³ = (2a)(6b³) = 12a6b³ = 12a⁷b³x⁶.

Let's simplify the given expressions:

Simplifying x² - 5x - 16:

To factorize this quadratic expression, we look for two numbers whose product is equal to -16 and whose sum is equal to -5. The numbers are -8 and 2.

Therefore, x² - 5x - 16 can be written as (x - 8)(x + 2).

Simplifying 6an² - 3b²n²:

To simplify this expression, we can factor out the common term n² from both terms:

6an² - 3b²n² = n²(6a - 3b²).

Simplifying 4x² - 4xy + y²:

This expression represents a perfect square trinomial, which can be factored as (2x - y)².

Simplifying n + 1 - n³ - n²:

Rearranging the terms, we have -n³ - n² + n + 1.

Combining like terms, we get -n³ - n² + n + 1 = -(n³ + n² - n - 1).

Simplifying 17x³y⁴z⁶:

To simplify this expression, we can divide each exponent by 2 to simplify it as much as possible:

17x³y⁴z⁶ = (x²y²z³)².

Simplifying 12a²b³:

To simplify this expression, we can multiply the exponents of a and b with the given expression:

12a²b³ = (2a)(6b³) = 12a6b³ = 12a⁷b³x⁶.

Learn more about  expression from

https://brainly.com/question/723406

#SPJ11

The solution of expression on algebraic fractions is,

⇒ y = 47/21

We have to given that;

Expression to simplify is,

⇒ 5/y + 1/7y - 2/3y = 2

Now, WE can simplify the expression as,

⇒ 5/y + 1/7y - 2/3y = 2

⇒ (35y + y)/7y² - 2/3y = 2

⇒ 36y/7y² - 2/3y = 2

⇒ 36/7y - 2/3y = 2

⇒ (108 - 14) / 21y = 2

⇒ 94 = 21y × 2

⇒ 94 = 42y

Divide both side by 42;

⇒ y = 94 / 42

⇒ y = 47/21

Therefore, The solution of expression on algebraic fractions is,

⇒ y = 47/21

Learn more about the fraction visit:

https://brainly.com/question/5454147

#SPJ1

Answer:

142.69

Step-by-step explanation:

142.70-0.01

is

142.69

Brainiest plz

Answer:

142.69

Step-by-step explanation:

A number 0.01 less than 142.7 is equal to 142.7 minus 0.01.

142.7 - 0.01 = 142.69.

Let me know if this helps!

The number of tickets sold on Friday were 66 children tickets and 97 adult tickets.

An equation is an expression that shows the relationship between two or more numbers and variables.

The equation of the parabola passing through (0, 0), (-3, 9) and (3, 9) is y = x²

The equation of the parabola with vertex at (4, 22) passing through (0, 6), (8, 6) and (3, 9) is y < -x² + 8x + 6

The solution to the system of equation is the darker region and it contains the point (-1, 6)

Find out more on equation at: https://brainly.com/question/2972832

#SPJ1

Answer:

(2,9)

Step-by-step explanation:

Got it on FlVS

Therefore, the solution to the system of equations is (x, y) = (-3, 4).

An equation is a mathematical statement that shows that two expressions are equal. It typically consists of two parts: the left-hand side (LHS) and the right-hand side (RHS), separated by an equal sign (=). The LHS and RHS can be composed of variables, constants, and mathematical operations such as addition, subtraction, multiplication, and division. Equations are used to solve problems in various fields such as physics, engineering, economics, and mathematics.

To solve the system of equations using elimination, we need to manipulate one or both equations so that one of the variables has the same coefficient with opposite signs. Here's how we can solve the system:

Multiply the first equation by -2 to get -4x - 10y = -28.

Add the second equation to the new equation to get -8y = -32.

Divide both sides by -8 to get y = 4.

Substitute y = 4 into either equation to solve for x.

Using the first equation:

\(2x + 5(4) = 14\)

\(2x + 20 = 14\)

\(2x = -6\)

\(x = -3\)

To learn more about equation, visit

https://brainly.com/question/10413253

#SPJ1

Answer:

I think -3

Step-by-step explanation:

Answer:

54 and 5

Step-by-step explanation:

56-2 is 54

7-5 is 2

have a good day my little friend learning his 1st addition

Answer:

Step-by-step explanation:

Answer:

\(H = \frac{V}{\pi r^{2} }\)

Step-by-step explanation:

So long as you have the volume and radius of a cylinder, it should be easy!

Simply divide the volume (V) of the cylinder by Pi Radius Squared (\(\pi r^{2}\)).

That is the formula for finding the height of a cylinder!

I hope this helped!

Answer:5

Step-by-step explanation:

Answer: \(x\leq -1\)

Step-by-step explanation: The closed point indicates that it can be equal to that number. The arrow is going back on the number line, meaning it is going to be less. Thus, it is less than or equal to -1.

The utility’s percent change from 2010 to 2020 is a decrease of 4.07%

How many years are between 2010 and 2020?

There are 10 years in between 2010 and the year 2020, which means that the total decline over a period of 10 years is the annual decrease multiplied by 10.

Total decrease in 10 years=2.6*10

Total decrease in 10 years=26.0

Utility industry jobs in 2020=639.5-26.0

Utility industry jobs in 2020=613.5

The percentage change 2010-2020=(2020 jobs/2010 jobs)-1

The percentage change 2010-2020=(613.5/639.5)-1

The percentage change 2010-2020=-4.07%

Find out more about percentage change on:https://brainly.com/question/17308462

#SPJ1

Answer:

1.22 grams of sugar

Step-by-step explanation:

8.54 divided by 7 is 1.22

The profit for the option writer is $3,900.

In this scenario, the option writer sold a put option on the Canadian dollar with an exercise price of USD 0.76/CAD. The premium received for the option was $0.039/CAD. The contract size is CAD 100,000, and the spot price at maturity is $0.76/CAD. However, since the spot price at maturity is equal to the exercise price of $0.76/CAD, the option is not exercised. As the option writer, the profit is determined by the premium received. In this case, the premium received per contract is $0.039/CAD. Multiplying this by the contract size of CAD 100,000, we get $3,900.

It's important to note that if the spot price at maturity had been lower than the exercise price, the option would have been exercised, resulting in a loss for the option writer equal to the difference between the exercise price and the spot price, multiplied by the contract size.

Learn more about price here:

https://brainly.com/question/19091385

#SPJ11

Answer:

The slope is 1/3 and the y intercept is 6

Step-by-step explanation:

The slope intercept form of a line is

y = mx+b where m is the slope and b is the y intercept

3y -x =18

Add x to each side

3y = x+18

Divide each side by 3

3y/3 = x/3 +18/3

y = 1/3x +6

The slope is 1/3 and the y intercept is 6

We need to solve for y (y = mx + b):

3y - x = 18

~Add x to both sides

3y = 18 + x

~Divide 3 to everything

y = 6 + x/3 or y = 6 + 1/3/x

So... 1/3 is the slope and 6 is the y-intercept.

Best of Luck!

We see that the measure of angle ORP is 80 degrees and the measure of angle ORN is (3x10) degrees. The statement that could be used in step 2 when proving x = 30 is "80 = 3x 10".

In step 2 of the proof, we need a statement that supports the claim that x is equal to 30. Looking at the given table, we see that the measure of angle ORP is 80 degrees and the measure of angle ORN is (3x10) degrees.

To prove that x is equal to 30, we can set up an equation based on the information provided:

80 = 3x 10

By simplifying the equation, we can solve for x:

80 = 30x

Dividing both sides of the equation by 30, we get:

x = 80/30

x = 8/3

x ≈ 2.67

However, the equation x = 30 is not satisfied by this value of x. Therefore, the given statement "80 = 3x 10" is incorrect or incomplete, and it cannot be used as a valid step in proving x = 30.

Learn more about measure of angle here:

https://brainly.com/question/31186705

#SPJ11

(t_{\text{half-empty}} = \frac{{50 - 2\sqrt{77}}}{{20 - 2\sqrt{77}}}) (days)

B. The remaining volume after 5 days:

(V(5) = \frac{{(4(20 - 2\sqrt{77}) + 2\sqrt{77})^2}}{4}) (liters)

[\frac{{dy}}{{dt}} - y = 8e^t + 12e^{5t}, \quad y(0) = 10]

To solve this, we use the method of integrating factors.

First, we rewrite the equation in the standard form:

[\frac{{dy}}{{dt}} - y = 8e^t + 12e^{5t}]

Next, we identify the integrating factor, which is the exponential of the integral of the coefficient of y.

In this case, the coefficient of y is −1, so the integrating factor is (e^{-t}).

Now, we multiply the entire equation by the integrating factor:

[e^{-t} \cdot \frac{{dy}}{{dt}} - e^{-t} \cdot y = 8e^t \cdot e^{-t} + 12e^{5t} \cdot e^{-t}]

Simplifying this equation gives:

[\frac{{d}}{{dt}} (e^{-t} \cdot y) = 8 + 12e^{4t}]

Integrating both sides with respect to t gives:

[\int \frac{{d}}{{dt}} (e^{-t} \cdot y) , dt = \int (8 + 12e^{4t}) , dt]

Integrating the left side gives:

[e^{-t} \cdot y = 8t + 3e^{4t} + C]

To find the constant of integration C, we use the initial condition y(0)=10:

[e^{-0} \cdot 10 = 8(0) + 3e^{4(0)} + C]

Solving this equation gives:

[10 = 3 + C]

So, C=7.

Substituting the value of C back into the equation gives:

[e^{-t} \cdot y = 8t + 3e^{4t} + 7]

Finally, solving for y gives:

[y = (8t + 3e^{4t} + 7) \cdot e^t]

Therefore, the solution to the initial value problem is:

[y = (8t + 3e^{4t} + 7) \cdot e^t]

(\frac{{dV}}{{dt}} = k \sqrt{V})

where (k) is the proportionality constant.

Given that 23 liters leak out during the first day, we can write the initial condition as:

(V(1) = 100 - 23 = 77) liters

To find the value of (k), we can substitute the initial condition into the differential equation:

(\frac{{dV}}{{dt}} = k \sqrt{V})

(\frac{{dV}}{{\sqrt{V}}} = k dt)

Integrating both sides:

(2\sqrt{V} = kt + C)

where (C) is the constant of integration.

Using the initial condition (V(1) = 77), we can find the value of (C) as follows:

(2\sqrt{77} = k(1) + C)

(C = 2\sqrt{77} - k)

Substituting back into the equation:

(2\sqrt{V} = kt + 2\sqrt{77} - k)

Now, let's answer the specific questions:

A. When will the tank be half empty? We want to find the time (t) when the volume (V(t)) is equal to half the initial volume.

(\frac{1}{2} \cdot 100 = 2\sqrt{77} + k \cdot t_{\text{half-empty}})

Simplifying:

(50 - 2\sqrt{77} = k \cdot t_{\text{half-empty}})

Solving for (t_{\text{half-empty}}):

(t_{\text{half-empty}} = \frac{{50 - 2\sqrt{77}}}{{k}})

When will the tank be half empty?

(t_{\text{half-empty}} = \frac{{50 - 2\sqrt{77}}}{{20 - 2\sqrt{77}}}) (days)

B. The remaining volume in the tank after 5 days can be found by substituting (t = 5) into the equation we derived:

(2\sqrt{V} = k \cdot 5 + 2\sqrt{77} - k)

Simplifying:

(2\sqrt{V} = 5k + 2\sqrt{77} - k)

(2\sqrt{V} = 4k + 2\sqrt{77})

Squaring both sides:

(4V = (4k + 2\sqrt{77})^2)

Simplifying:

(V = \frac{{(4k + 2\sqrt{77})^2}}{4})

The value of (k) can be determined from the initial condition:

(2\sqrt{100} = k \cdot 1 + 2\sqrt{77})

(20 = k + 2\sqrt{77})

(k = 20 - 2\sqrt{77})

The remaining volume after 5 days:

(V(5) = \frac{{(4(20 - 2\sqrt{77}) + 2\sqrt{77})^2}}{4}) (liters)

Learn more about initial value problem:

https://brainly.com/question/30883066

#SPJ11