Jeremy performs the same operations on 4 values for x. He records each resulting y-value in a table, which equation shows the operation Jeremy performs on x to get to y?
x: 2,4,6,8
y:5,13,21,29
Answers: y= 2x+1 , y= 4x-3 , y= x+3 , y= 3x-1
Answers
Answer:
y= 2x+1
Step-by-step explanation:
Related Questions
Consider a Markov chain which at each transition either goes up 1 with probability p or down 1 with probability q = 1 - p. Argue that (q/p)^Sn , n >= 1 is a martingale.
Answers
The (q/p)^Sn, n>=1 is a martingale.
To show that (q/p)^Sn, n>=1 is a martingale, we need to show that it satisfies the three conditions of a martingale:
The expected value of (q/p)^Sn is finite for all n.
For all n, E[(q/p)^Sn+1 | Fn] = (q/p)^Sn, where Fn is the sigma-algebra generated by the first n transitions.
(q/p)^Sn is adapted to the filtration Fn.
First, we note that the expected value of (q/p)^Sn is finite for all n since q/p < 1, and thus (q/p)^n approaches zero as n approaches infinity.
Next, we consider the second condition. Let F_n be the sigma-algebra generated by the first n transitions, and let X_n = (q/p)^Sn. We need to show that E[X_n+1 | F_n] = X_n.
We can write (q/p)^(n+1) = (q/p)^n * (q/p), so we have:
E[X_n+1 | F_n] = E[(q/p)^(n+1) | F_n]
= E[(q/p)^n * (q/p) | F_n]
= (q/p)^n * E[(q/p) | F_n]
= (q/p)^n * [(q/p) * P(up) + (p/q) * P(down)]
= (q/p)^n * [(q/p) * p + (p/q) * q]
= (q/p)^n * (p + q)
= (q/p)^n * 1
= X_n
Thus, the second condition is satisfied.
Finally, we need to show that X_n is adapted to the filtration F_n. This is true since X_n only depends on the first n transitions, which are included in F_n.
Therefore, we have shown that (q/p)^Sn, n>=1 is a martingale.
Learn more about markov chain at https://brainly.com/question/30544880
#SPJ11
Anyone know the answer to this question it’s about polynomials?!!?!

Answers
Answer:
Step-by-step explanation:
x+2) x^3+0x^2+0x-4(x^2-2x+4
x^3+2x^2
- -
_______________
-2x^2+0x
-2x^2-4x
+ +
____________
4x-4
4x+8
- -
______
-12
_____
\(\frac{x^3-4}{x+2} =x^2-2x+4+\frac{-12}{x+2}\)
Alice is going to make a cake for her mother's birthday. It will take 24 minutes to make the cake batter, and the cake needs to bake in the oven for 1 hour and 2 minutes. If Alice wants the cake to be out of the oven by 9:59 A.M., what is the latest time she can start making the cake batter?
Answers
The latest time Alice can start making the cake batter is 8:33 A.M
How to calculate the latest time ?Alice is making cake for her mother's birthday
It will take 24 minutes to make the cake batter
The cake also needs to be in the oven for 1 hour 2 minutes
The time needed to make the cake is
1 hour 2 minutes + 24 minutes
= 1 hour 26 minutes
The latest time to start making the cake batter is
9:59 - 1:26
= 8:33
Hence the latest time to start making the cake batter is 8:33 A.M
Read more on time here
https://brainly.com/question/18246829?referrer=searchResults
#SPJ1
Consider the polynomial function f(x) - x4 -3x3 + 3x2 whose domain is(-[infinity], [infinity]). (a) Find the intervals on which f is increasing. (Enter you answer as a comma-separated list of intervals.) Find the intervals on which f is decreasing. (Enter you answer as a comma-separated list of intervals.) (b) Find the open intervals on which f is concave up. (Enter you answer as a comma-separated list of intervals.) Find the open intervals on which f is concave down. (Enter you answer as a comma-separated list of intervals.) (c) Find the local extreme values of f. (If an answer does not exist, enter DNE.) local minimum value local maximum value Find the global extreme values of f onthe closed-bounded interval [-1,2] global minimum value global maximum value (e) Find the points of inflection of f. smaller x-value (x, f(x)) = larger x-value (x,f(x)) =
Answers
a. f is increasing on (-∞,0) and (1/2,∞), and decreasing on (0,1/2) and (1,∞).
b. f is concave down on (-∞,1/2) and (3/2,∞), and concave up on (1/2,3/2).
c. The local minimum value is 0 and the local maximum value is -5/16.
d. The global minimum value is -8 at x = 2, and the global maximum value is 8 at x = -1.
e. The smaller x-value inflection point is (1/2, -5/16) and the larger x-value inflection point is (3/2, 25/16).
What is inflexion point?
The point of inflection, also known as the inflection point, is when the function's concavity changes. Changing the function from concave down to concave up, or vice versa, signifies that.
(a) To find the intervals on which f is increasing or decreasing, we need to find the critical points of f and determine the sign of the derivative on the intervals between them.
The derivative of f(x) is:
f'(x) = 4x³ - 9x² + 6x = 3x(2x-1)(2x-2)
The critical points are the values of x where f'(x) = 0 or f'(x) is undefined.
Setting f'(x) = 0, we get:
3x(2x-1)(2x-2) = 0
This gives us the critical points x = 0, x = 1/2, and x = 1.
Since f'(x) is defined for all x, there are no other critical points.
Now we can test the sign of f'(x) on each interval:
On (-∞,0), f'(x) is negative because 3x, (2x-1), and (2x-2) are all negative.
On (0,1/2), f'(x) is positive because 3x is positive and (2x-1) and (2x-2) are negative.
On (1/2,1), f'(x) is negative because 3x is positive and (2x-1) and (2x-2) are positive.
On (1,∞), f'(x) is positive because 3x, (2x-1), and (2x-2) are all positive.
Therefore, f is increasing on (-∞,0) and (1/2,∞), and decreasing on (0,1/2) and (1,∞).
(b) To find the intervals on which f is concave up or down, we need to find the inflection points of f and determine the sign of the second derivative on the intervals between them.
The second derivative of f(x) is:
f''(x) = 12x² - 18x + 6 = 6(2x-1)(2x-3)
The inflection points are the values of x where f''(x) = 0 or f''(x) is undefined.
Setting f''(x) = 0, we get:
6(2x-1)(2x-3) = 0
This gives us the inflection points x = 1/2 and x = 3/2.
Since f''(x) is defined for all x, there are no other inflection points.
Now we can test the sign of f''(x) on each interval:
On (-∞,1/2), f''(x) is negative because 2x-1 and 2x-3 are both negative.
On (1/2,3/2), f''(x) is positive because 2x-1 is positive and 2x-3 is negative.
On (3/2,∞), f''(x) is negative because 2x-1 and 2x-3 are both positive.
Therefore, f is concave down on (-∞,1/2) and (3/2,∞), and concave up on (1/2,3/2).
(c) To find the local extreme values of f, we need to look at the critical points we found earlier and determine whether they correspond to local maximum or minimum values.
At x = 0, f(0) = 0⁴ - 3(0)³ + 3(0)² = 0, so this is a local minimum.
At x = 1/2, f(1/2) = (1/2)⁴ - 3(1/2)³ + 3(1/2)² = -5/16, so this is a local maximum.
At x = 1, f(1) = 1⁴ - 3(1)³ + 3(1)² = 1, so this is a local minimum.
Therefore, the local minimum value is 0 and the local maximum value is -5/16.
(d) To find the global extreme values of f on the closed-bounded interval [-1,2], we need to evaluate f at the critical points and endpoints of the interval.
At x = -1, f(-1) = (-1)⁴ - 3(-1)³ + 3(-1)² = 8.
At x = 0, f(0) = 0.
At x = 1/2, f(1/2) = -5/16.
At x = 1, f(1) = 1.
At x = 2, f(2) = 2⁴ - 3(2)³ + 3(2)² = -8.
Therefore, the global minimum value is -8 at x = 2, and the global maximum value is 8 at x = -1.
(e) To find the points of inflection of f, we can use the inflection points we found earlier: (1/2, -5/16) and (3/2, 25/16).
The smaller x-value inflection point is (1/2, -5/16) and the larger x-value inflection point is (3/2, 25/16).
To learn more about inflexion point from the given link
https://brainly.com/question/29249123
#SPJ4
180º represent chocolate, 90º represent vanilla and 90º represents other flavor draw the pie chart.
will be marked as brainliest
Answers
Answer:
Look at attached.
Step-by-step explanation:
A full circle is 360 degrees. So 180 represents half of the circle and 90 represents a quarter.

Answer:
chocolate 180°
Step-by-step explanation:
chocolate=180°
vanilla=90°
othere flavor=90°
the total degrees of the pie chart 360 °
Please hurry!! 50 points! I will mark brainliest!!!
What is the slope of the line on the graph?

Answers
Answer:
-12/6 or -2
Step-by-step explanation:

Answer:
-2
Step-by-step explanation:
Gradient = slop
(-3,6)
(3,-6)
\(gradient \: = \frac{difference \: of \: y \: }{difference \: of \: x} \)
\(gradient \: = \frac{6 - ( - 6)}{ - 3 - 3} \)
= 12/-6
= - 2
Solve the following logarithmic equation. (5 points) log2 (x2 - 6x + 20) = 3
Answers
The solutions to the logarithmic equation log2(x2-6x+20) = 3 are x = 3 + i√3 and x = 3 - i√3.
Given: log2(x2-6x+20) = 3
To solve this logarithmic equation, we use the basic definition of logarithms, which is a way of writing an exponential equation in a shorter form.
In this case, we can rewrite the equation as:
2³ = x² - 6x + 20
Since 2³ = 8, the equation becomes:
8 = x² - 6x + 20Subtracting 8 from both sides:
0 = x² - 6x + 12
We can now use the quadratic formula to solve for x,
which is given by:
x = (-b ± √(b² - 4ac)) / 2a
Where a = 1, b = -6, and c = 12.
Substituting these values into the formula, we get:
x = (-(-6) ± √((-6)² - 4(1)(12))) / 2(1)x = (6 ± √(36 - 48)) / 2x = (6 ± √(-12)) / 2x = (6 ± 2i√3) / 2x = 3 ± i√3
Thus, the solutions to the logarithmic equation log
2(x2-6x+20) = 3 are
x = 3 + i√3 and
x = 3 - i√3.
To know more about logarithmic visit:
https://brainly.com/question/30226560
#SPJ11
Andre is reviewing proportional relationships. He wants to practice using a graph that goes through a point so that each coordinate is between 1 and 10. a. For the point, how many outcomes are in the sample space? b. For how many outcomes are the x-coordinate and the y-coordinate the same number?
Answers
Answer:
1. 100
2. 10
Step-by-step explanation:
There are 100 different outcomes because each number can pair with another number 10 times or an easy way to do it is just to do 10x10 which is 100.
For number 2 the answer is 10 because each x and y have one number that is the same for example x and y both have 1,2,3,4,5... and so on. So therefore each number can pair to itself once and the numbers are 1-10.
Hope I could help.
PLS HELP!!!!
Select the correct comparison.
Set A
Set B
.
. . .
278 10
0268
A. The typical value is greater in set A. The spread is greater in set B.
B. The typical value and the spread are both greater in set A.
C. The typical value and the spread are both greater in set B.
D. The typical value is greater in set B. The spread is greater in set A.
Answers
Two friends, Carson and William, took summer jobs. Carson earned $451.50 in 21
hours. How much less per hour does William earn than carson
Answers
when conducting an analysis of variance, you are comparing two components of variance. which two components are you comparing? in order for you to reject the null hypothesis, which component has to be statistically larger?
Answers
The statistical analysis method known as analysis of variance (ANOVA) divides the observed aggregate variability within a data set into two parts:
Systematic factorsRandom factors.The presented data set is statistically affected by the systematic factors but not by the random ones.You reject the hull hypothesis if the difference between your data and the null hypothesis is greater than the critical value but not if it is less than the critical value.The variance components can be estimated using one of four distinct techniques: analysis of variance (ANOVA), maximum likelihood (ML), restricted maximum likelihood (RML), and minimum norm quadratic unbiased estimator (MINQUE) (REML). There are numerous specifications available for the various procedures.When the p-value is less than or equal to your significance level, reject the null hypothesis. The alternative theory, which contends that the effect is widespread, is supported by your sample data. As a mnemonic device, keep in mind that the null must be removed when the p-value is low.To learn more about analysis of variance
https://brainly.com/question/15062874
#SPJ4
Calculate the slope of the line that contains
(-2,-4) and (6, 7)
Answers
Answer:
m=11/8
Step-by-step explanation:
(x1,y1)=(−2,−4)
(x2,y2)=(6,7)
-Use slope formula-
m=y2−y1/x2−x1
=7− −4/ 6− −2
=11/8
6th grade please help!

Answers
Answer:
68
Step-by-step explanation:
F = 1.8(20)+32 = 68
Small earthworms travel at speeds of about 0.2 centimeters per second. What is this speed in meters per second? 0.0002 meters per second 0.002 meters per second 20 meters per second 200 meters per second
Answers
Answer: 0.002 meters per second
Step-by-step explanation:
Answer:
The answer is b.
Step-by-step explanation:
I took the test and got it right.
A soft drink manufacturing company produces tins with orange juice with a mean weight of 25 ounces. A sample of 50 tins is selected to test whether overfilling or underfilling is occurring and they should stop and adjust it. Sample statistics (mean and standard deviation) are calculated. Assume the population of interest is normally distributed
The p-value for this test can be calculated in Excel using the function
1 − NORM.S.DIST(|z-stat|, TRUE)
2 ∗ (1 − NORM.S.DIST(|z-stat|, TRUE))
T.DIST.RT(|t-stat|, 49)
2 ∗ (1 − T.DIST(|t-stat|, 49, TRUE))
Answers
The correct formula to calculate the p-value for this test would depend on whether a z-test or t-test is being used.
If the population standard deviation is known, then a z-test would be appropriate. The formula for the p-value using a z-test would be:
p-value = 2 (1 - NORM.S.DIST(|z-stat|, TRUE))
where z-stat is the calculated test statistic (in units of the standard error), and NORM.S.DIST is the standard normal cumulative distribution function in Excel.
If the population standard deviation is unknown and is estimated using the sample standard deviation, then a t-test would be appropriate. The formula for the p-value using a t-test would be:
p-value = 2 (1 - T.DIST(|t-stat|, df))
where t-stat is the calculated test statistic (in units of the standard error), df is the degrees of freedom (equal to n-1 for a sample of size n), and T.DIST is the cumulative distribution function for a t-distribution in Excel.
In this case, the sample size is 50 and the population standard deviation is unknown, so a t-test would be appropriate. The degrees of freedom would be 49, and the formula for the p-value would be:
p-value = 2 (1 - T.DIST(|t-stat|, 49, TRUE))
where T.DIST is the cumulative distribution function for a t-distribution in Excel, and the TRUE argument specifies that the cumulative distribution function should return the area to the right of the test statistic.
It's worth noting that the absolute value signs around the test statistic (|t-stat|) and the use of the two-sided test (multiplying by 2) are necessary because this is a two-tailed test to determine whether the mean weight of the tins is different from 25 ounces (i.e., whether there is either overfilling or underfilling).
To learn more about the z score;
https://brainly.com/question/15016913
#SPJ1
A university is researching the impact of including seaweed in cattle feed. They assign feed with and without seaweed to be fed to cows at two
different dairy farms. The two-way table shows randomly collected data on 200 dairy cows from the two farms about whether or not their feed
includes seaweed.
Based on the data in the table, if a cow is randomly selected from farm B, what is the probability that its feed includes seaweed?
Without Seaweed?
A. 0.649
B. 0.620
C. 0.370
D. 0.597

Answers
Based on the data in the table, if a cow is randomly selected from farm B, the probability that its feed includes seaweed is 0.597 (Option D) and without is 0.57
How did we arrive at this?Note that the total number of feed with sea weed is 74.
And the total number of cows on the farm B is 124.
Thus, the cows whose feed includes seaweed is 74/124
= 0.59677419354
≈ 0.597
The Probability of those whose feed is without sea weed is
Note that the total number of feed without sea weed is 40.
And the total number of cows on the farm B is 76.
Thus, the probability is 40/70
= 0.5714285714
≈ 0.571
Learn more about probability:
https://brainly.com/question/30034780
#SPJ1
Help me please
a) The upper bound for the area of the rectangle.
b) The lower bound for the perimeter of the rectangle.

Answers
Answers:
Part (a) upper bound for area = 4527.7056 square cmPart (b) lower bound for perimeter = 278 cm======================================================
Explanation:
Part (a)
The horizontal portion is shown to be 87.3 cm long. This is the result after rounding has occurred. Specifically, rounding to one decimal place (tenths). The question is: What could the number have been before rounding?
You have to think in reverse of the usual rounding process.
The values 87.25, 87.26, 8.27, ... 8.33, 87.34 all round to 87.3 when we round to one decimal digit. Note the hundredths digit is increasing by 1 each time. We can see that 87.34 is the largest possible value for the horizontal piece. After that, 87.35 will round to 87.4 which is just out of reach.
Through similar logic/reasoning, the vertical side can be at most 51.84 cm.
The area of the rectangle could be 87.34*51.84 = 4527.7056 which is the upper bound for the area. This is the largest possible area, given the values in the diagram, since we made each value as large as possible.
In short, 4527.7056 square cm is the max area.
-----------------------------------
Part (b)
We use the idea of part (a), but we'll use the smallest possible values this time.
So we go with 87.25 for the horizontal portion and 51.75 for the vertical portion.
Compute the perimeter with these smallest dimensions.
P = 2*(length + width)
P = 2*(87.25 + 51.75)
P = 278
The smallest perimeter possible is 278 cm which is the lower bound of the perimeter. This is guaranteed to be the smallest perimeter possible because we made the sides as small as possible, while staying in the restrictions as discussed in the previous section.
Given the function defined in the table below, find the average rate of change, in simplest form, of the function over the interval 4≤x≤8.
Answers
Answer:
No Solution
Step-by-step explanation:
It's false there's no solution
Find the volume of the triangular prism.
NO LINKS THEY WILL BE REPORTED
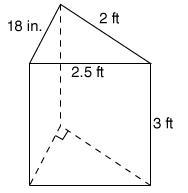
Answers
Answer:
4.5 ft³
Step-by-step explanation:
Volume = 1/2(LxWxH)
1/2( 1.5 x 2) * 3 = 1.5 x 3 = 4.5 ft ³
If my answer is incorrect, pls correct me!
If you like my answer and explanation, mark me as brainliest!
-Chetan K
Find the next 3 terms of the following sequence -4,-9,-14
Find the next 3 terms of the following sequence 3,12,48
Answers
Answer:
-19,-24,-29
192,768,3072
Step-by-step explanation:
for the first equation its going down by 5
for the second its multiplying by 4 everytime
Jack and Jill share £200 sweets in the ratio 7:3
Work out how much each person gets.
Answers
Answer:
jack= £140
Jill= £60
Step-by-step explanation:
7+3= 10= total amount of parts
200/10=20
1 part-20
7*20=140 (jack)
3*20=60(jill)
Mrs. Chen wrote two checks and made a deposit of $1,987.09 since her october statement. The october statement shows a balance of $3,611.08, and her checkbook shows she currently has $2,778.09. What is the total amount of the checks that Mrs. Chen wrote?
Answers
Rotate this figure 270 degrees clockwise

Answers
Answer:
it's the third answer
Step-by-step explanation:
360 degrees is a full circle so you subtract the 90 degrees from it and get 270. The only turn it would need to be a full 360 is 90 degrees. hope this helps
Answer:
its the one pointing to the right
Step-by-step explanation:
if its pointing down then goes 180 clockwise, then it will be pointing straight up, then 270-180 is 90 so it goes 90 degrees clockwise.
It is a Saturday morning, and Jeremy has discovered he has a leak coming from the water
heater in his attic. Since plumbers charge extra to come out on weekends. Jeremy is
planning to use buckets to catch the dripping water. Ile places a bucket under the drip and
steps outside to walk the dog. In half an hour, the bucket is 1/5 of the way full.
Answers
Answer:
He will need 9.6 buckets per day. If that was the question...
Step-by-step explanation:
If it takes half an hour for it to fill up 1/5 of the way, then in an hour it will have filled up 2/5 of the way.
2/5 x 24 = 9 3/5 or 9.6
Solve the inequality
|3x+4|>6
Answers
Answer:
x > 2/3 or x < -10/3
Step-by-step explanation:
|3x + 4| > 6
To solve an absolute value inequality of the form |X| > b, where X is an expression, and b is a number, change the inequality into this compound inequality:
X > b or X < -b
Here, X is 3x + 4.
b is 6.
We get the compound inequality:
3x + 4 > 6 or 3x + 4 < -6
3x > 2 or 3x + 4 < -6
x > 2/3 or 3x < -10
x > 2/3 or x < -10/3
Answer:
\(\left(- \infty, -\dfrac{10}{3}\right) \cup \left(\dfrac{2}{3}, \infty\right)\)
Step-by-step explanation:
To solve an inequality containing an absolute value:
Isolate the absolute value on one side of the equation.Apply the relevant absolute rule.Solve both cases.Given inequality:
\(|3x+4| > 6\)
Apply the absolute rule:
\(\textsf{If }\:|u| > a,\:a > 0\:\textsf{ then }\:u < -a \:\textsf{ or }\: u > a\)
Therefore:
\(\begin{aligned}\text{\underline{Case 1}} && \text{\underline{Case 2}}\\3x+4 & < -6 \quad & 3x+4 & > 6\\3x & < -10 \quad & 3x & > 2\\x & < -\dfrac{10}{3} \quad & x & > \dfrac{2}{3}\end{aligned}\)
So the solution to the inequality in interval notation is:
\(\left(- \infty, -\dfrac{10}{3}\right) \cup \left(\dfrac{2}{3}, \infty\right)\)
2. A triangle has a side length of 2 inch and a side length of 3 inches. What could be the length, in inches, of the third side of the triangle? Complete the response grid in the Answer Document.
Answers
Answer
the third side can measure 2 in, 3 in, or 4 in
Explanation
inequality theorem
a + b > c
a + c > b
b + c > a
2 = a
b = 3
c = x
a + b > c
2 + 3 > x
5 > x
x= 4, 3, 2, or 1 in
a + c > b
2 + x > 3
x = 4, 3, or 2
b + c > a
3 + x > 2
x = 4, 3, or 2
Determine the zero-state response, Yzs(s) and yzs(t), for each of the LTIC systems described by the transfer functions below. NOTE: some of the inverse Laplace transforms from problem 1 might be useful. (a) Î11(s) = 1, with input Êi(s) = 45+2 (b) Ĥ2(s) = 45+1 with input £2(s) (C) W3(s) = news with input £3(s) = 542. (d) À4(8) with input Ê4(s) = 1 s+3. s+3 2e-4 4s = s+3 = 4s+1 s+3.
Answers
In a linear time-invariant system, the zero-state response (ZSR) is the output of the system when the input is zero, assuming all initial conditions (such as initial voltage or current) are also zero.
(a) For H1(s) = 1, the zero-state response Yzs(s) is simply the product of the transfer function H1(s) and the input Ei(s):
Yzs(s) = H1(s) * Ei(s) = (45+2)
To find the time-domain zero-state response yzs(t), we need to take the inverse Laplace transform of Yzs(s):
yzs(t) = L^-1{Yzs(s)} = L^-1{(45+2)} = 45δ(t) + 2δ(t)
where δ(t) is the Dirac delta function.
(b) For H2(s) = 45+1, the zero-state response Yzs(s) is again the product of the transfer function H2(s) and the input E2(s):
Yzs(s) = H2(s) * E2(s) = (45+1)E2(s)
To find the time-domain zero-state response yzs(t), we need to take the inverse Laplace transform of Yzs(s):
yzs(t) = L^-1{Yzs(s)} = L^-1{(45+1)E2(s)} = (45+1)e^(t/2)u(t)
where u(t) is the unit step function.
(c) For H3(s) = ns, the zero-state response Yzs(s) is given by:
Yzs(s) = H3(s) * E3(s) = ns * 542
To find the time-domain zero-state response yzs(t), we need to take the inverse Laplace transform of Yzs(s):
yzs(t) = L^-1{Yzs(s)} = L^-1{ns * 542} = 542L^-1{ns}
Using the inverse Laplace transform from problem 1, we have:
yzs(t) = 542 δ'(t) = -542 δ(t)
where δ'(t) is the derivative of the Dirac delta function.
(d) For H4(s) = 2e^(-4s) / (s+3)(4s+1), the zero-state response Yzs(s) is given by:
Yzs(s) = H4(s) * E4(s) = (2e^(-4s) / (s+3)(4s+1)) * (1/(s+3))
Simplifying the expression, we have:
Yzs(s) = (2e^(-4s) / (4s+1))
To find the time-domain zero-state response yzs(t), we need to take the inverse Laplace transform of Yzs(s):
yzs(t) = L^-1{Yzs(s)} = L^-1{(2e^(-4s) / (4s+1))}
Using partial fraction decomposition and the inverse Laplace transform from problem 1, we have:
yzs(t) = L^-1{(2e^(-4s) / (4s+1))} = 0.5e^(-t/4) - 0.5e^(-3t)
Therefore, the zero-state response for each of the four LTIC systems is:
(a) Yzs(s) = (45+2), yzs(t) = 45δ(t) + 2δ(t)
(b) Yzs(s) = (45+1)E2(s), yzs(t) = (45+1)e^(t/2)u(t)
(c) Yzs(s) = ns * 542, yzs(t) = -542 δ(t)
(d) Yzs(s) = (2e^(-4s) /
To learn more about derivative visit:
brainly.com/question/30365299
#SPJ11
Find the area of this composite figure.

Answers
Answer: 242 in²
All the work is shown in the picture.

The figure is a parallelogram. m

Answers
Answer:
10
Step-by-step explanation:
a 4 side polygon has 360° interior angle
120 +120=240
360-240=120
120÷2=60
60÷6=10
Neeeed helpppp nowwww!!!!!

Answers
I think the answer is the second one?