Jason drops a tennis ball outside of his hotel balcony. He is standing 52 feet above the street. If the ball hits the hotel canopy 12 feet above street-level, how long after Jason releases the ball will it hit the canopy. Use the function h(t) = -16t2 + 52. Round your answer to the nearest tenth.
Jason drops a tennis ball outside of his hotel balcony. He is standing 52 feet above the street. If the ball hits the hotel canopy 12 feet above street-level, how long after Jason releases the ball will it hit the canopy. Use the function h(t) = -16t2 + 52. Round your answer to the nearest tenth.
1.6 seconds
2.0 seconds
0.4 seconds
4.0 seconds
Answers
1.6 seconds. The ball will hit the canopy after 1.58 seconds or -1.58 seconds. Since the time cannot be negative, the ball will hit the canopy after 1.58 seconds.
How to find time ?To find the time it takes for the ball to hit the canopy, we need to solve the equation h(t) = 12 for t.
The given equation for h(t) is h(t) = -16t^2 + 52, so we can substitute this into the equation h(t) = 12 to get:
12 = -16t^2 + 52
To solve this equation, we can move all the terms to one side of the equation to get:
-16t^2 + 40 = 0
We can then divide both sides of the equation by -16 to get:
t^2 - 2.5 = 0
We can then use the quadratic formula to solve for t:
t = +/- sqrt(2.5)
t = +/- 1.58
Thus, the ball will hit the canopy after 1.58 seconds or -1.58 seconds. Since the time cannot be negative, the ball will hit the canopy after 1.58 seconds.
Rounding this answer to the nearest tenth gives us 1.6 seconds, so the correct answer is 1.6 seconds.
To learn more about time refer :
brainly.com/question/13088717
#SPJ1
Related Questions
ABC is an equilateral triangle.
If the mZA-7x -9.1.
Find the value of x rounded to the nearest tenth. (If your answer is exact. nlease nut at the end

Answers
Answer:
x = 9.9Step-by-step explanation:
An equilateral triangle is the triangle with equal interior angles.
Each angle has measure of 60°, therefore:
m∠A = 60°Substitute and solve for x:
7x - 9.1 = 607x = 69.1x = 69.1/7x = 9.9 (rounded)Measure of all angles in equilateral triangle is 60°
So
m<A=607x-9.1=607x=69.1x=9.9A subcommittee is randomly selected from a committee of eight men and seven women. What is the probability that all three people on the subcommittee are men
Answers
Answer:
The probability that all three people on the subcommittee are men
= 20%
Step-by-step explanation:
Number of members in the committee = 15
= 8 men + 7 women
The probability of selecting a man in the committee
= 8/15
= 53%
The probability of selecting three men from eight men
= 3/8
= 37.5%
The probability that all three people on the subcommittee are men
= probability of selecting a man multiplied by the probability of selecting three men from eight men
= 53% x 37.5%
= 19.875%
= 20% approx.
This is the same as:
The probability of selecting 3 men from the 15 member-committee
= 3/15
= 20%
I need help completing this problem ASAP

Answers
Answer:
\(4\sqrt{5}\)
Step-by-step explanation:
Prime factorize 20 and 45
\(\sqrt{20}=\sqrt{2*2*5}=2\sqrt{5}\\\\\\\sqrt{45}= \sqrt{5*3*3}=3\sqrt{5}\)
\(\sqrt{20}-\sqrt{5}+\sqrt{45}=2\sqrt{5}-\sqrt{5}+3\sqrt{5}\)
\(=(2-1+3)\sqrt{5}\\\\\\= 4\sqrt{5}\\\)
Find the PERIMETER and AREA of each figure below
help ASPS
Find the perimeter and area 22-24 and only find the area for 25-26

Answers
Answer:
22)
\(2(length+breadth+h)\)\(2(5a^2b^2+3ab^2)\)\(Perimeter: 2ab^2(5a^2+31)\)\(Area:-\)
\(5a^2b^4 *3ab^2\)\(A=15a^2b^6\)-----------
23)
\(perimeter:-\)
\(4m^2+3mn^2+7mn\)\(4m^2+10mn^2\)\(answer: 2m(2m+5n^2)\)\(Area:-\)
\(\frac{1}{2}* base* height\)\(1/2*3mn^2*4m^2\)\(6mx^{2+1}n^2\)\(A=6m^3n^2\)----------
24)
\(1/2*b*h\)\(1/2x^24m^2*8mn\)\(A=16m^3n\)----------
25)
\(1/2*(7a^2b+11a^2b)*3ab\)\(1/2*18a^2b*3ab\)\(9a^2b*3ab\)\(A=27 a^3b^2\)------------
26)
\(A= 9\pi (x^3y)^2\)∴To calculate the perimeter , add the length of its sides.
∴To calculate the area, multiply its height by its width.
------------------------
hope it helps...
have a great day!!
What is the solution set of the equation (x – 2)(x – a) = 0?
A –2 and a
B –2 and –a
C 2 and a
D 2 and –a
E 2 only
Answers
C 2 and a
Simplify: 9( 1 - r ) + 3r

Answers
Answer:
9-6r
Step-by-step explanation:
9(1−r)+3r
Use the distributive property to multiply 9 by 1−r.
9−9r+3r
Combine −9r and 3r to get −6r.
Answer: 9−6r
Answer:
-6r + 9
Step-by-step explanation:
9( 1 - r ) + 3r
9 - 9r + 3r
9 - 6r
So, the answer is -6r + 9
Given two planes how do I find the vector equation?

Answers
The vector equation for the intersection of the two planes is given by:
9i + 36j - 24k.
What is the vector equation for the intersection of two planes?Suppose that we have two planes, defined as follows:
ax + by + cz = K1. (K1 constant).dx + ey + fz = K2. (K2 constant).The vector equation for the intersection between these two places is given by the determinant of the following matrix:
\(\left[\begin{array}{ccc}i&j&k\\a&b&c\\d&e&f\end{array}\right]\)
For this problem, the planes are:
6y + 9z = 39.4x + 3y + 6z = 10.Hence the matrix of which we have to find the determinant is:
\(\left[\begin{array}{ccc}i&j&k\\0&6&9\\4&3&6\end{array}\right]\)
The determinant of the 3 x 3 matrix is given by:
D = i x 6 x 6 + j x 9 x 4 + k x 0 x 3 - (k x 6 x 4 + j x 0 x 6 + i x 9 x 3).
D = 36i + 36j - (24k + 27i)
D = 36i + 36j - 24k - 27i
D = 9i + 36j - 24k.
Which is the vector equation.
More can be learned about the vector equation for the intersection of the two planes at https://brainly.com/question/8837203
#SPJ1
At an arcade, a book of 20 tickets costs $5, a book of 30 tickets costs $7, and a book of 50 tickets costs $10. Would a graph of the relationship between price and number of tickets in a book be a straight line? Explain.
Answers
Answer:
yes
Step-by-step explanation:
Which of the systems of linear equations will have no solution?
Question 15 options:
y = 12 – 3x
y = 2x – 3
y = x – 1
-5x + y = -5
2x + y = 9
2x + y = 5
y = 2x
3x + 2y = 21
Answers
The system of equations given in option 4, y = 2x and 3x + 2y = 21, will have no solution.
2x + y = 9
2x + y = 5
The graph is attached
How to find the equation without solutionA system of linear equations will have no solution if the lines represented by the equations are parallel, meaning they have the same slope but different y-intercepts.
Looking at the given options:
y = 12 – 3x
y = 2x – 3
y = x – 1
-5x + y = -5
2x + y = 9
2x + y = 5
y = 2x
3x + 2y = 21
Option 3, 2x + y = 9 and 2x + y = 5, represents parallel lines.
The slopes of the lines are the same (both equations have a coefficient of -2 for x and 1 for y), but the y-intercepts are different
Learn more about linear equation at
https://brainly.com/question/28732353
#SPJ1

Find a third degree polynomial that passes through the points (−3, 0),(−2, −3),(0, 3) and (2, −15). Using the form p(x) = ax3+bx2+cx+d.
Answers
Answer:
f(x)=3/16x^3-9/4x+3
Solve the given initial-value problem. The DE is a Bernoulli equation.
, 1/2 dy + y3/2 = 1, y(0) = 16
dx
2
3
x
2
|
co
y = 1 + 63e
x
Show all work correctly

Answers
Your solution seems fine. What does the rest of the error message say?
\(\displaystyle y^{1/2}\frac{\mathrm dy}{\mathrm dx} + y^{3/2} = 1\)
Substitute
\(z(x)=y(x)^{3/2} \implies \dfrac{\mathrm dz}{\mathrm dx}=\dfrac32y(x)^{1/2}\dfrac{\mathrm dy}{\mathrm dx}\)
to transform the ODE to a linear one in z :
\(\displaystyle \frac23\frac{\mathrm dz}{\mathrm dx} + z = 1\)
Divide both sides by 2/3 :
\(\displaystyle \frac{\mathrm dz}{\mathrm dx} + \frac32z = \frac32\)
Multiply both sides by the integrating factor, \(e^{3x/2}\) :
\(\displaystyle e^{3x/2}\frac{\mathrm dz}{\mathrm dx} + \frac32 e^{3x/2}z = \frac32 e^{3x/2}\)
Condense the left side into the derivative of a product :
\(\displaystyle \frac{\mathrm d}{\mathrm dx}\left[e^{3x/2}z\right] = \frac32 e^{3x/2}\)
Integrate both sides and solve for z :
\(\displaystyle e^{3x/2}z = \frac32 \int e^{3x/2}\,\mathrm dx \\\\ e^{3x/2}z = e^{3x/2} + C \\\\ z = 1 + Ce^{-3x/2}\)
Solve in terms of y :
\(y^{3/2} = 1 + Ce^{-3x/2}\)
Given that y (0) = 16, we have
\(16^{3/2} = 1 + Ce^0 \implies C = 16^{3/2}-1 = 63\)
so that the particular solution is
\(\boxed{y^{3/2} = 1 + 63e^{-3x/2}}\)
draw the line passing through the point (0,2) with a slope of -1
Answers
Answer:
y = -x + 2
Step-by-step explanation:
Given the function defined in the table below, find the average rate of change, in simplest form, of the function over the interval 0\le x \le 150≤x≤15.
x f(x)
0 9
3 39
6 69
9 99
12 129
15 159
Answers
So the average rate of change of the function over the interval 0 ≤ x ≤ 15 is 4.4.
What is function?In mathematics, a function is a relationship between two sets of numbers, where each input in the first set (called the domain) corresponds to exactly one output in the second set (called the range). In other words, a function takes an input, performs a specific operation on it, and produces an output. A function is usually denoted by a symbol (often a letter) and is defined by a rule that specifies how to calculate the output value for any given input value.
Here,
To find the average rate of change of the function over the interval 0 ≤ x ≤ 15, we need to calculate the change in the function value divided by the change in x over the interval.
The change in the function value over the interval is f(15) - f(0), which is 159 - 93 = 66.
The change in x over the interval is 15 - 0 = 15.
Therefore, the average rate of change of the function over the interval 0 ≤ x ≤ 15 is:
average rate of change = change in f / change in x
= 66 / 15
= 4.4
To know more about function,
https://brainly.com/question/28278699
#SPJ1
In KLM, KM is extended through point M to point N,
(3x +19)°, m/LMN = (7x + 5)°, and
m/KLM = (2x+8)°. What is the value of x?
Answers
The value of the variable "x" is 11.
We have a triangle. The vertices of the triangle are K, L, and M. The side KM is extended from point M to point N. The measures of the angles MKL, LMN, and KLM are (3x + 19)°, (7x + 5)°, and (2x + 8)°, respectively. We need to find out the value of the variable "x".
The angles LMK and LMN form a linear pair. It means they are supplementary angles. The sum of the angles is 180°.
∠LMK + ∠LMN = 180°
∠LMK + (7x + 5)° = 180°
∠LMK = 180° - (7x + 5)°
In the triangle KLM, we will use the angle sum property of a triangle. The sum of all the angles in a triangle is equal to 180°.
∠K + ∠L + ∠M = 180°
(3x +19)° + (2x + 8)° + [180° - (7x + 5)°] = 180°
3x +19 + 2x + 8 + 180 - 7x - 5 = 180
-2x + 22 = 0
2x = 22
x = 11
Hence, the value of the variable "x" is 11.
To learn more about variables, visit :
https://brainly.com/question/22277991
#SPJ9
f(x) = -2x^2+3x-6
how does the function open
Answers
4.1.3 Bathu Sneakers have been looking into different shoebox sizes: a large box for male shoes and small box for female shoes. The cost of the cardboard to make the boxes is 0,502 cents/cm². Calculate the percentage savings Bathu Sneakers will make if the smaller box is used compared to the normal larger box. Larger Box Total Surface Area = 4 093 cm² 19 cm 26 cm 34,5 cm Smaller Box Total Surface Area = 3 034 cm² 25 cm 17 cm 26 cm (6)
Answers
Answer:
Step-by-step explanation:To calculate the savings percentage, we first need to find out the cost of the cardboard required for each box.
For the larger box:
Total Surface Area = 2 * (1926 + 1934.5 + 26*34.5) = 2 * (494 + 655.5 + 897) = 4093 cm²
Cost of cardboard for larger box = 0.502 * 4093 = 2055.986 cents = 20.55986 dollars (rounded to 5 decimal places)
For the smaller box:
Total Surface Area = 2 * (2517 + 2526 + 1726) + 6 * (25-21)* (17-2*1) = 3034 cm²
Note that the additional term in the equation is the surface area of the six sides of the lid and base of the box.
Cost of cardboard for smaller box = 0.502 * 3034 = 1522.268 cents = 15.22268 dollars (rounded to 5 decimal places)
The difference in cost between the larger and smaller boxes is:
20.55986 - 15.22268 = 5.33718 dollars (rounded to 5 decimal places)
The percentage savings can be calculated as follows:
Percentage savings = (difference in cost / cost of larger box) * 100%
= (5.33718 / 20.55986) * 100%
= 25.98%
Therefore, using the smaller box will result in a savings of approximately 26% on cardboard costs for Bathu Sneakers compared to using the normal larger box.
PLZZZ HELP ME PLZZZ IM STUCK IF U DO HELP ME I LOVEEE YOUUU (^.^)

Answers
Answer:
The answer is A. -21
Step-by-step explanation:
-21. J(x)= -4(5)= -20 ; H[J(5)]= -20-1 = -21
I NEED AN ANSWER!! PLEASE
Solve for x: 5(x + 3) = 4(x − 3) (1 point) −18 −27 −3 −6
Answers
Answer:
\(-27\)
Step-by-step explanation:
\(5(x+3)=4(x-3) \\ \\ 5x+15=4x-12 \\ \\ x+15=-12 \\ \\ x=-27\)
Multiply and combine like terms to determine the product of these polynomials. (3x−6)(4x+1)
Answers
= 12x^2 - 21x -6

What is the domain and range of the function Y=2x-4
Answers
Answer:
Domain: all real numbers
Range: all real numbers
Compare the investment below to an investment of the same principal at the same rate compounded annually.
principal: $5,000, annual interest: 9%, interest periods: 4, number of years: 18
After 18 years, the investment compounded periodically will be worth $? more than the investment compounded annually.
(Round to two decimal places as needed.)
Answers
After 18 years, the investment compounded periodically (quarterly) will be worth $1,230.23 more than the investment compounded annually.
What is compounded interest?Compounded interest refers to the interest system that charges interest on both principal and accumulated interest.
The period of compounding in a year determines the worth of the future value.
The future value can be ascertained using an online finance calculator as follows:
Interest periods: = 4 times yearly (Quarterly)
Principal = $5,000
Annual interest rate = 9%
Number of years: 18
N (# of periods) = 72 quarters (18 years x 4)
I/Y (Interest per year) = 9%
PV (Present Value) = $5,000
PMT (Periodic Payment) = $0
Results:
Future Value (FV) = $24,815.83
Total Interest = $19,815.83
Interest periods: = Annually
N (# of periods) = 18 years
I/Y (Interest per year) = 9%
PV (Present Value) = $5,000
PMT (Periodic Payment) = $0
Results:
Future Value (FV) = $23,585.60
Total Interest = $18,585.60
Difference in Future Values $1,230.23 ($24,815.83 - $23,585.60)
Thus, an investment compounded periodically earns more than an investment compounded annually.
Learn more about compounded interest at https://brainly.com/question/28020457.
#SPJ1
help with this it is so hard

Answers
Answer:
its 4.8
Step-by-step explanation:
i divided 7.5 by 12.5 and got 0.6 and added 4.2 and got 4.8
Answer:
here is your answerrrrrrrrrrr

100 Points! Multiple choice Geometry question. Photo attached. Thank you!

Answers
Answer:
2. C. 50.3 ft²
3. A. 75.4 ft²
Step-by-step explanation:
The lateral surface area of a cylinder is the area of the curved surface of the cylinder. It is calculated by multiplying the circumference of the base by the height of the cylinder. The formula for the lateral surface area of a cylinder is:
Lateral Surface Area = 2πrh
Where:
r is the radius of the baseh is the height of the cylinderThe total surface area of a cylinder is the area of the lateral surface plus the area of the two circular bases. The formula for the total surface area of a cylinder is:
Total Surface Area = 2πrh + 2πr^2
Where:
r is the radius of the baseh is the height of the cylinder2.
r=2 ft
h=4 ft
Lateral Surface Area = 2πrh=2*22/7*2*4=50.3 ft²
3.
Total Surface Area = 2πrh + 2πr^2=2*22/7*2*4+2*22/7*2
=50.3+25.1=75.4 ft²
Which of the following methods would provide a voluntary response sample?
A.
B.
C.
D.

Answers
Answer:
The Answer is D
Step-by-step explanation:
A survey of every 10th person leaving a large shopping mall. I hope im right this question was tricky though. Hope it helps :)
I am stuck please help with this graph.
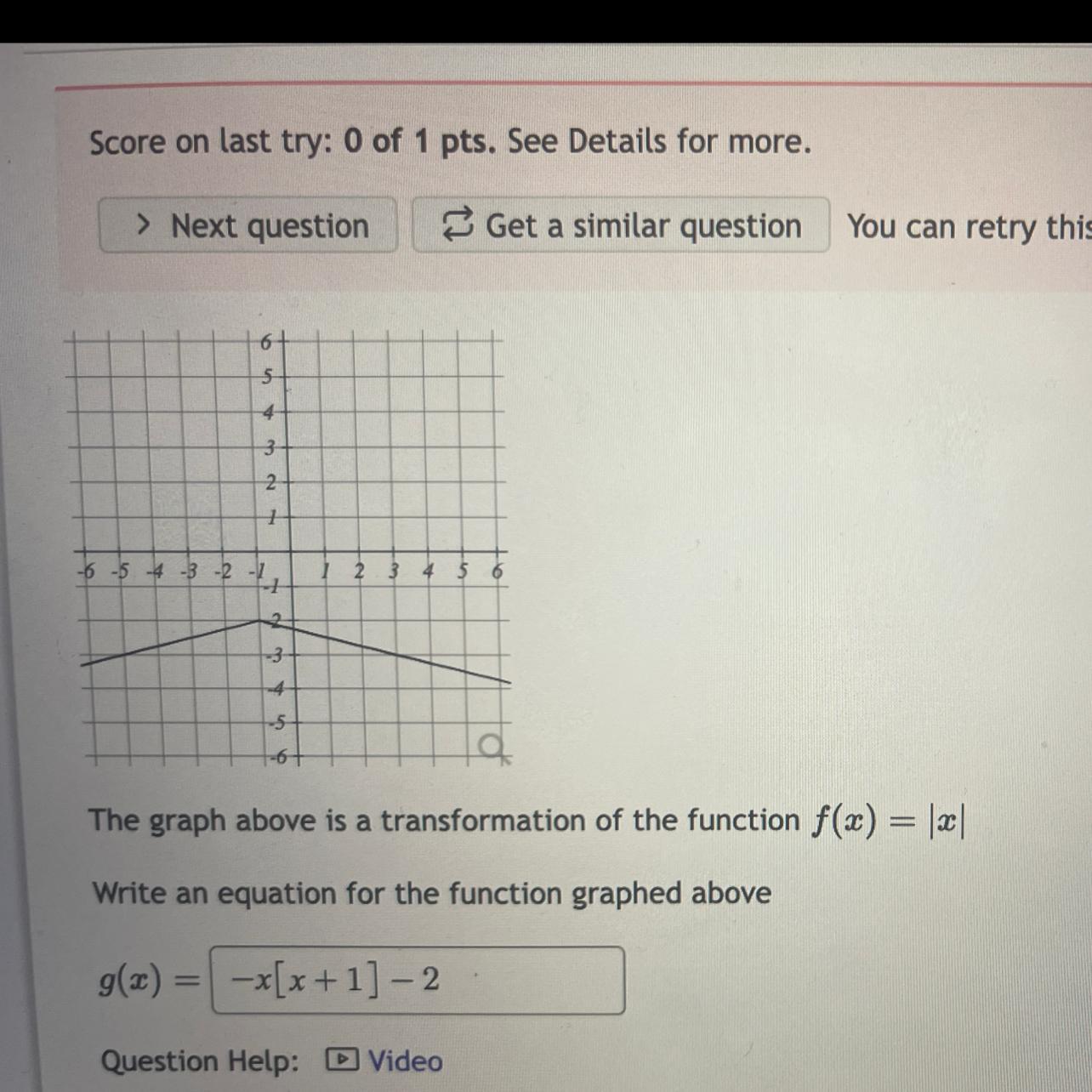
Answers
An equation for the function graphed above include the following: g(x) = -1/4|x + 1| - 2.
How to interpret and determine the equation of g(x)?By critically observing the graph of this absolute value function, we can reasonably infer and logically deduce that the parent absolute value function f(x) = |x| was vertically compressed by a factor of 1/4, reflected over the x-axis, followed by a vertical translation 2 units down, and then a horizontal translation to the left by 1 unit, in order to produce the transformed absolute value function as follows;
f(x) = |x|
y = A|x + B| + C
g(x) = -1/4|x + 1| - 2
In conclusion, the value of the variables A, B, and C are -1/4, 1, and 2 respectively.
Read more on absolute value function here: brainly.com/question/28308900
#SPJ1
• Riley and her sister collect stickers. Riley has 220 stickers
in her sticker collection. Her sister has 55 stickers in her
collection. Riley has how many times as many stickers as
her sister? Use mental math or the guess, check, and
revise strategy to solve the equation 55x = 220.
Answers
Answer:
Riley has 4 times the amount of stickers her sister has
Step-by-step explanation:
220 divided by 55 is 4
Let S- (1,2,3,4,5,6) (a) How many subsets are there total? (b) How many subsets contain the elements 2,3 and 5? o) How many subsets contain at least one odd number? (d) How many subsets contain exactly one even number? (e) How many subsets are there of cardinality 4? (f) How many subsets of cardinality 4 contain the elements 2,3, and 5? (g) How many subsets of cardinality 4 contain at least one odd number? (h) How many subsets of cardinality 4 contain exactly one even number?
Answers
a) There are 2^6 = 64 subsets total.
b) There are 2^3 = 8 subsets total
c) There are 2^5 = 32 subsets total
d) There are 32^4 = 48 subsets total
e) There are (6 choose 4) = 15 subsets total
f) There are 32 = 6 subsets total
g) There are is (6 choose 4) - (3 choose 4) = 15 - 0 = 15 subsets total
h) There are (3 choose 1) * (3 choose 3) = 3 subsets total
a) There are 2^6 = 64 subsets total.
b) Since we need to include elements 2, 3, and 5 in a subset, we have 3 elements fixed, and we need to choose 1, 2, or 3 elements from the remaining 3 elements (1, 4, and 6). Therefore, there are 2^3 = 8 subsets that contain the elements 2, 3, and 5.
c) There are 2^5 = 32 subsets that contain at least one odd number. This can be seen by noticing that if a subset does not contain any odd numbers, then it must be {2,4,6}, which is not a valid subset since it does not satisfy the condition that it be a subset of S.
d) There are 32^4 = 48 subsets that contain exactly one even number. To see why, notice that there are 3 choices for which even number to include (2, 4, or 6), and then there are 2^4 = 16 choices for which of the remaining 4 odd numbers to include in the subset.
e) There are (6 choose 4) = 15 subsets of cardinality 4. This is the number of ways to choose 4 elements from a set of 6.
f) Since we need to include elements 2, 3, and 5 in a subset of cardinality 4, we have 3 elements fixed, and we need to choose 1 element from the remaining 3 even elements, and 1 element from the remaining 2 odd elements. Therefore, there are 32 = 6 subsets of cardinality 4 that contain the elements 2, 3, and 5.
g) The number of subsets of cardinality 4 that contain at least one odd number is equal to the total number of subsets of cardinality 4 minus the number of subsets of cardinality 4 that contain only even numbers. This is (6 choose 4) - (3 choose 4) = 15 - 0 = 15.
h) The number of subsets of cardinality 4 that contain exactly one even number is equal to the number of ways to choose 1 even number out of 3, and then the number of ways to choose 3 odd numbers out of 3. This is (3 choose 1) * (3 choose 3) = 3.
To learn more about subsets:
https://brainly.com/question/2280091
#SPJ4
find the unit measure of ADI need help with this

Answers
From properties of lines inscribed in circles we will have that:
\(\begin{gathered} AD+DB=AB:AD=DB \\ \\ \Rightarrow2AD=AB\Rightarrow AD=\frac{AB}{2} \\ \\ \Rightarrow AD=\frac{60}{2}\Rightarrow AD=30 \end{gathered}\)So, the measure of AD is 30 units.
The area of a circle is 4/pi cm. What is the circumference in centimeters express your answers in terms of pi
Answers
Answer:
4 cm.
Step-by-step explanation:
Area = pi r^2, so:
pi r^2 = 4 / pi
(pi)^2 r^2 = 4
r^2 = 4/ (pi^2)
r = 2/pi
Therefore, the circumference
= 2 pi r
= 2* pi * 2/pi
= 4
Tennis starts moving at 4m/s to the left. for 5s he is accelerating at a constant rate of 3m/s^2. what is his final velocity
Answers
The final velocity of the Tennis for the condition is 19 m/s.
What is acceleration?acceleration: the rate at which the speed and direction of a moving object vary over time. A point or object going straight ahead is accelerated when it accelerates or decelerates. Even if the speed is constant, motion on a circle accelerates because the direction is always shifting.
Given Tennis starts moving at 4m/s to the left,
initial speed = 4 m/s
for 5s he is accelerating at a constant rate of 3m/s^2
time = t = 5 s
acceleration = 3 m/s²
to find the final velocity,
velocity is given by,
v = u + at
u = initial speed, t = time, and a = acceleration
v = 4 + 3(5)
v = 4 + 15
v = 19 m/s
Hence velocity is 19 m/s.
Learn more about acceleration;
https://brainly.com/question/12550364
#SPJ1