Janet is designing a garden in her backyard that is a regular octagon with a side length of 6 ft and an apothem of 7.24
ft. What is the approximate area of the garden?
O 72 ft2
O 347.5 ft2
O 173.8 ft2
O 86.9 ft2
Answers
Answer:
c. \(\sf area \ of \ octagon = 173.82 \ ft^2\)
Explanation:
\(\sf area \ of \ octagon = 2(1+\sqrt{2} )a^2\)
Here "a" refers to side length.
using this formula:
\(\hookrightarrow \sf area \ of \ octagon = 2(1+\sqrt{2} )(6)^2\)
\(\hookrightarrow \sf area \ of \ octagon = 173.82 \ ft^2\)
Solution:
It should be noted:
Area of regular octagon: 2(1 + √2)x² (x = side)Substitute the side length into the formula.
2(1 + √2)x²=> 2(1 + √2) × 6²Simplify the distributive property.
=> 2(1 + √2)36=> 72(1 + √2)=> 72 + 72√2Simplify 72√2 using a calculator.
=> 72 + 101.82Add if needed.
=> 173.82 ft²Looking at the options, it is said that option C is correct as 173.8 and 173.82 are approximate numbers.
Option C is correct.
Related Questions
The vertices of YEAR are Y(1,-4) E(3,0), A (-1,2) and R( -3,-2) . prove that YEAR is a Square

Answers
To prove that YEAR is a square, we need to show that all four sides have the same length and all four angles are right angles (90 degrees).
Side Lengths: To find the lengths of the sides, we can use the distance formula:
d = √((x2 - x1)² + (y2 - y1)²)
For example, to find the length of the side that connects Y and E, we can use the following calculation:
d = √((3 - 1)² + (0 - (-4))²) = √((2)² + (4)²) = √(4 + 16) = √20
We can use the same formula to calculate the lengths of the other sides. By doing so, we will find that the length of all four sides are the same, which is √20. This means that all four sides of YEAR are congruent, and therefore it is a square.
If A and B are invertible n×n matrices, then the inverse of A+B is A−1+B−1.
True or False
Answers
The statement is false since when A = Iₙ and B = -Iₙ, then A+B = 0ₙ, which is not invertible.
Given that:
A and B are invertible n×n matrices.
It is required to check if the inverse of A + B is A⁻¹ + B⁻¹.
Let A = Iₙ, which is the identity matrix, and B = -Iₙ, which is the negative of the identity matrix.
It is known that the inverse of an identity matrix of order n is the same identity matrix of order n.
So, A⁻¹ = Iₙ and B⁻¹ = -Iₙ
Now,
A + B = Iₙ - Iₙ = 0ₙ.
It is known that zero matrices are not invertible.
So, the statement is not true.
Hence the correct option is E.
Learn more about Invertible Matrices here :
https://brainly.com/question/31116922
#SPJ4
A rectangular pool is surrounded by a walk 4 feet wide. The pool is 6 feet longer than it is wide. The total area is 272 square. What are the dimensions of the pool
Answers
The width of the pool is 18 feet, and the length is 24 feet (since it is 6 feet longer than the width).
Let's represent the width of the pool as x. Then, the length of the pool would be x + 6.
The total area of the pool and walk is given by:
Total area = (length + 2(4)) × (width + 2(4))
Total area = (x + 6 + 8) × (x + 4)
Total area = (x + 14) × (x + 4)
The area of the pool itself is given by:
Pool area = length × width
Pool area = x(x + 6)
Pool area = x² + 6x
We're told that the total area is 272 more than the area of the pool:
Total area = Pool area + 272
(x + 14) × (x + 4) = x² + 6x + 272
Expanding the left side of the equation:
x² + 18x + 56 = x² + 6x + 272
Simplifying the equation:
12x = 216
Solving for x:
x = 18
So the width of the pool is 18 feet, and the length is 24 feet (since it is 6 feet longer than the width).
Learn more about the width
https://brainly.com/question/29281920
#SPJ4
Full Question: A rectangular pool is surrounded by a walk 4 feet wide. The pool is six feet longer than its wide. If the total area is 272 ft² more than the area of the pool,what are the dimension of the pool?
please help me!
in ∆ ABC the two interior angles 25° (x+15°) are non -adjecen to an exterior angle (3x-10°) then find x.
Answers
Given the above problem involving interior and exterior angles, the value of x = 70°
What is an exterior angle?External angles are those that are parallel to a polygon's inner angles but are on the outside of it. The sum of two internal opposing angles equals the measure of an outside angle.
In this case the exterior angle is: (3x-10°). See attached image.
Thus, we can find x by using the principle of the Sum of an interior angle of a triangle.
Since all interior angles of a triangle sum up to 180°, then
If the missing side is x,
x° + 25° + (x+15°) = 180°
To solve the equation x° + 25° + (x+15°) = 180° for x, you first need to simplify the left-hand side of the equation:
x + 25 + (x+15) = 180
Combine like terms: 2x + 40 = 180
Now simplify: 2x = 140
Divide both sides by 2: x = 70
Therefore, the solution to the equation is x = 70.
Thus, (3x-10°)
If x = 70, then:
3x - 10° = 3(70) - 10°
= 210° - 10°
= 200° (Exterior Angle)
Also, (x+15°) if x = 70° is solved as:
If x = 70, then:
x + 15° = 70 + 15°
= 85°
To show that the computations are correct,
let's add all interior angles:
70+25+85 = 180°
Learn more about exterior angles:
https://brainly.com/question/28835566
#SPJ1

1000
900
800
Q3.A landscaping company offers their services as following:
$240 for a full landscape plan, plus $30 per hour to do the work
Display this data on the grid below. Label carefully both the axes.Identify the variables and explain why
you think this is a linear relation. What is the initial value for the relation and the rate of change.
Time (hours)
Cost ($)
6
2
4
8
10
12
14
0
Answers
The independent variable is time (hours), and the dependent variable is cost ($). The given relation is linear because it has a constant rate of change. The initial value for this relation is $240 and the rate of change is $30 per hour.
The table for the given relation is
Time (hours) Cost ($)
0 240
2 300
4 360
6 420
8 480
10 540
12 600
14 660
In this relation, the independent variable is time (hours), and the dependent variable is cost ($). The time is the input to the relation, and the cost is the output that is dependent on the input.
We can see that this relation is linear because it has a constant rate of change. The cost increases by $30 for each hour of work, which means that the slope of the line is constant.
The initial value for this relation is $240, which represents the cost of the full landscape plan. The rate of change is $30 per hour, which represents the additional cost for each hour of work. Therefore, the equation for this linear relation is
Cost = 30 x Time + 240
where "Cost" is the cost in dollars, "Time" is the time in hours, 30 is the rate of change, and 240 is the initial value.
To know more about relation here
https://brainly.com/question/14736401
#SPJ1
Find the perimeter of the sector. With an angle of 110 degrees and a radius of 8
Answers
Answer:
49 / 9π + 16
Step-by-step explanation:
So 110 / 360 = 11 / 36
The circumference of the circle is 16π
11 / 36 * 16 = 44 / 9π
44 / 9π + 8 + 8 is the answer since you gotta add the sides.
This might be wrong so check my steps.
x-5+2x-7 find the vale pleaser!!

Answers
Answer:
12
Step-by-step explanation:
They are the same angle so they must be equal.
So, x+5 = 2x-7
5+7 = 2x-x
12 = x
find the value of X, y and z
ans: x=50 y= 50 z=50

Answers
The value of x , y and z in the parallel line is 50 degrees.
How to find the angle in parallel line?When parallel lines are crossed by a transversal line, angle relationships are formed such as vertically opposite angles, alternate interior angles, alternate exterior angles, adjacent angles, corresponding angles etc.
Therefore, let's use the angle relationships to find the angle, x, y and z as follows:
Therefore,
x = 360 - 310(sum of angles in a point)
x = 50 degrees
Therefore,
x = y(alternate interior angles)
Alternate interior angles are congruent.
Hence,
y = 50 degrees
Therefore,
x = z(alternate interior angles)
z = 50 degrees.
learn more on angles here: https://brainly.com/question/17043791
#SPJ1
The z, t, and F calculations have something common: the denominator of the test statistic:a. contains a measure of difference among means.b. contains a measure of sample variability.c. is a squared number.d. represents what would be expected if the null hypothesis were true.
Answers
The denominator of the z, t, and F calculations all contain a measure of sample variability. This is because these calculations are used to determine the significance of a difference between sample means or proportions, and the measure of sample variability in the denominator is used to standardize the difference between the sample statistics.
The measure of sample variability is usually expressed as a squared number, which is the variance or standard deviation of the sample.
Additionally, the denominator represents what would be expected if the null hypothesis were true, as it reflects the amount of variability that would be observed in the sample if the null hypothesis were true and there was no real difference between the groups being compared.
To know more about denominator visit:
https://brainly.com/question/15007690
#SPJ11
Suppose that an investment has 0.5% chance of a loss of $10
million and a 99.5% chance of a loss of $1 million. What is the
Value-at-Risk (VaR) for this investment when the confidence level
is 99%
Answers
To calculate the Value-at-Risk (VaR) for this investment at a 99% confidence level, we need to determine the loss amount that will be exceeded with a probability of only 1% (i.e., the worst-case loss that will occur with a 1% chance).
Given that there is a 0.5% chance of a loss of $10 million and a 99.5% chance of a loss of $1 million, we can express this as:
Loss Amount | Probability
$10 million | 0.5%
$1 million | 99.5%
To calculate the VaR, we need to find the loss amount that corresponds to the 1% probability threshold. Since the loss of $10 million has a probability of 0.5%, it is less likely to occur than the 1% threshold. Therefore, we can ignore the $10 million loss in this calculation.
The loss of $1 million has a probability of 99.5%, which is higher than the 1% threshold. This means that there is a 1% chance of the loss exceeding $1 million.
Therefore, the Value-at-Risk (VaR) for this investment at a 99% confidence level is $1 million.
The Value-at-Risk (VaR) for this investment at a 99% confidence level is $1,045,000.
To calculate the Value-at-Risk (VaR) for this investment at a 99% confidence level, we need to determine the loss amount that will be exceeded with only a 1% chance.
Given that the investment has a 0.5% chance of a loss of $10 million and a 99.5% chance of a loss of $1 million, we can calculate the VaR as follows:
VaR = (Probability of Loss of $10 million * Amount of Loss of $10 million) + (Probability of Loss of $1 million * Amount of Loss of $1 million)
VaR = (0.005 * $10,000,000) + (0.995 * $1,000,000)
VaR = $50,000 + $995,000
VaR = $1,045,000
Therefore, the Value-at-Risk (VaR) for this investment at a 99% confidence level is $1,045,000.
To learn more about 99% confidence level
https://brainly.com/question/15873157
#SPJ11
A triangular prism is 12 meters long and has a triangular face with a base of 8 meters and a height of 9 meters. What is the volume of the triangular prism?
Answers
The volume of the triangular prism is 216 cubic meters.
To find the volume of a triangular prism, we need to multiply the area of the triangular base by the length of the prism.
Calculate the area of the triangular base.
The base of the triangular face is given as 8 meters, and the height is 9 meters. We can use the formula for the area of a triangle: area = (1/2) * base * height.
Plugging in the values, we get:
Area = (1/2) * 8 meters * 9 meters = 36 square meters.
Multiply the area of the base by the length of the prism.
The length of the prism is given as 12 meters.
Volume = area of base * length of prism = 36 square meters * 12 meters = 432 cubic meters.
Adjust for the shape of the prism.
Since the prism is a triangular prism, we need to divide the volume by 2.
Adjusted Volume = (1/2) * 432 cubic meters = 216 cubic meters.
Therefore, the volume of the triangular prism is 216 cubic meters.
For more such information on volume of triangular prism, visit:
https://brainly.com/question/31637705
#SPJ8
Simplify.
410 x 45 ÷ 49 = 4[?]
![Simplify.410 x 45 49 = 4[?]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/ZXLjvoKvMToUm8VlTsXDLoWDsncKjspS.png)
Answers
Hello !!
kᵃ x kᵇ = kᵃ⁺ᵇ
kᵃ ÷ kᵇ = kᵃ⁻ᵇ
4¹⁰ x 4⁵ ÷ 4⁹
= 4¹⁰⁺⁵ ÷ 4⁹
= 4¹⁵ ÷ 4⁹
= 4¹⁵⁻⁹
= 4⁶
at the city museum, child admission is and adult admission is . on thursday, twice as many adult tickets as child tickets were sold, for a total sales of . how many child tickets were sold that day?
Answers
After considering all the given data we conclude that total sales of child tickets sold that day is 29, under the condition that thursday, twice as many adult tickets as child tickets were sold.
Let us consider the number of child tickets sold as `c` and the number of adult tickets sold as `a`.
It is known that the child admission is $6.30 and adult admission is $9.60. The day concerning the data was Tuesday, in which adult tickets twice as many as child tickets were sold, resulting in a total sales of $739.50.
We can form two algebraic expressions based on this information:
a = 2c (adult tickets twice as many as child tickets were sold)
6.3c + 9.6a = 739.5 (total sales of $739.50)
Staging the first equation into the second equation gives:
6.3c + 9.6(2c) = 739.5
6.3c + 19.2c = 739.5
25.5c = 739.5
c = 29
Hence, child tickets sold on that day were 29 .
To learn more about algebraic expression
https://brainly.com/question/2164351
#SPJ1
The complete question is
At the city museum, child admission is 6.30 and adult admission is 9.60. On tuesday, twice as many adult tickets as child tickets were sold, for a total sales of 739.50. How many child tickets were sold that day?
What is the slope and y-intercept

Answers
Answer:
Step-by-step explanation:
the slope is 4 y intercept is 5
When you answer please show your work.

Answers
Answer:
C
Step-by-step explanation:
If we have some polynomial, P(x), and some real number,r, and the value of P(r)=0
then
\(x - r\)
is a factor of of the polynomial.
So since p(5)=0, then
\(x - 5\)
is a factor of the polynomial
C
what is this answer??
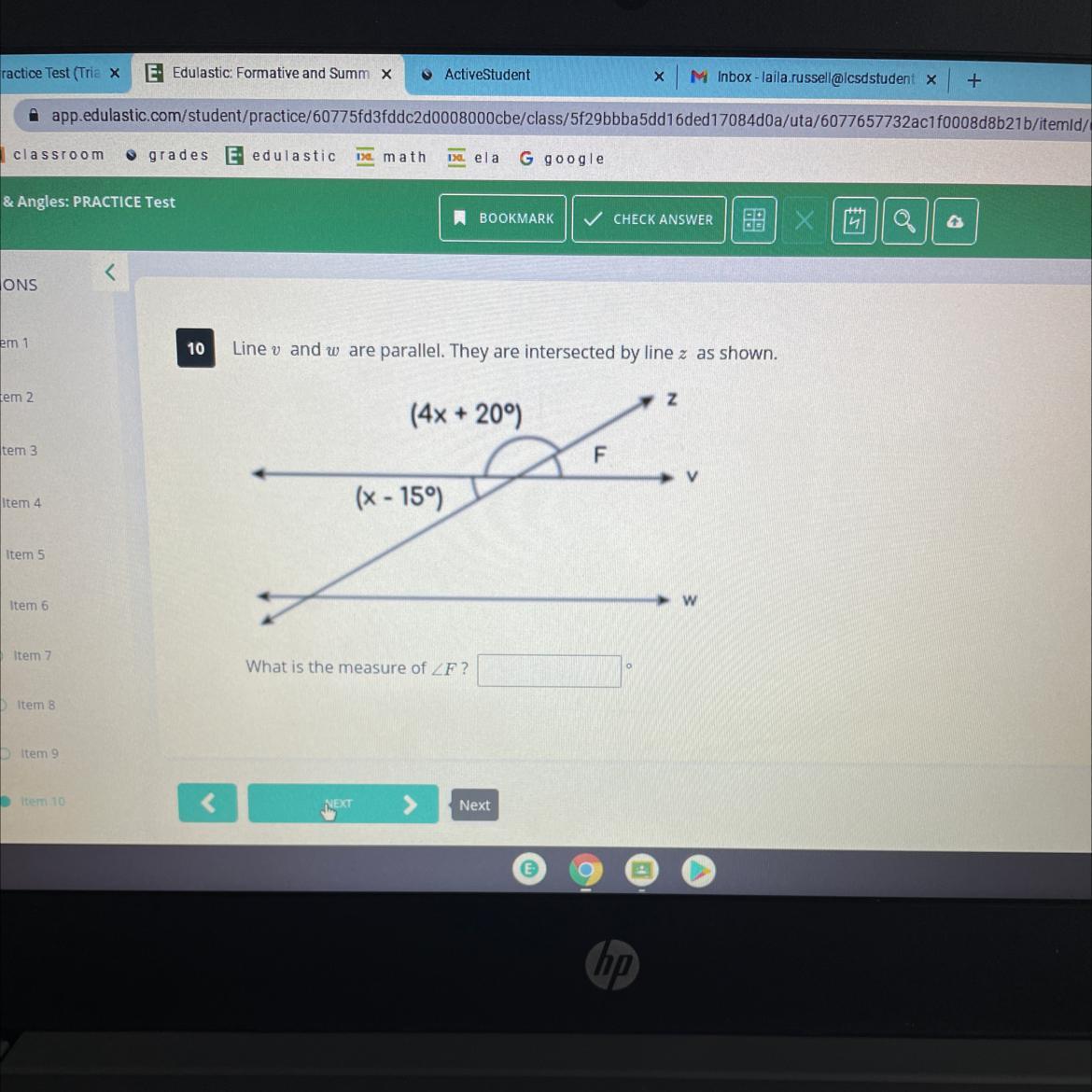
Answers
Answer:
\(20^{\circ}\)
Step-by-step explanation:
We can see here that the two unknown angles are on the straight line . So its measure will be 180° .
\(\implies (4x + 20^{\circ})+(x-15^{\circ}) = 180^{\circ} \\\\\implies 5x + 5^{\circ} = 180^{\circ} \\\\\implies 5x = 175^{\circ} \\\\\implies x =\dfrac{175^{\circ}}{5}\\\\\implies x = 35^{\circ} \)
Now the angle F and the angle (x-15)° are vertically opposite angles . So they will be equal .
\(\implies x - 15^{\circ} \\\\\implies 35^{\circ} - 15^{\circ} \\\\\implies \boxed{ 20^{\circ} } \)
The GCF of 14 and 42 is 2. True or False
The GCF of 16 and 56 is 8. True or False
Answers
4. What are the Z-scores for the following Confidence Interval levels? Remember, you MUST account for both tails of the curve, positive and negative, when identifying each. That means you will need to do a little math to obtain the correct z-value. 3 Points 68%= 85% = 99% =
Answers
In order to calculate the z-scores for the given Confidence Interval (CI) levels, we need to use the Z-table. It is also known as the standard normal distribution table. Here are the z-scores for the given Confidence Interval levels:1. 68% CI: The confidence interval corresponds to 1 standard deviation on each side of the mean.
Thus, the z-score for the 68% \(CI is ±1.00.2. 85% CI\): The confidence interval corresponds to 1.44 standard deviations on each side of the mean.
We can calculate the z-score using the following formula:\(z = invNorm((1 + 0.85)/2)z = invNorm(0.925)z ≈ ±1.44\)Note that invNorm is the inverse normal cumulative distribution function (CDF) which tells us the z-score given a certain area under the curve.3. 99% CI: The confidence interval corresponds to 2.58 standard deviations on each side of the mean. We can calculate the z-score using the following formula:\(z = invNorm((1 + 0.99)/2)z = invNorm(0.995)z ≈ ±2.58\)
Note that in general, to calculate the z-score for a CI level of (100 - α)% where α is the level of significance, we can use the following formula:\(z = invNorm((1 + α/100)/2)\) Hope this helps!
To know more about distribution visit:
https://brainly.com/question/29664127
#SPJ11
Mr. Smith is 81 years older than his grandson, Victor. In 3 years, Mr. Smith will be four times as old as Victor. How old is Victor now?
A) 21 years old
B) 22 years old
C) 24 years old
D) 27 years old
Answers
After 3 years 4(x+3)= x+81+3
4x+12= x +84
4x-x= 84–12= 72
3x = 72. Or x = 24
Now Victor's age is 24 and Mr. Smith is 105
In three years Victor will be 27and Mr. Smith will be 108 (four times of 27)
A store manager kept track of the number of newspapers sold each week over a seven-week period. The results are shown below. \( 87,87,215,154,288,235,231 \) Find the median number of newspapers sold.
Answers
The median number of newspapers sold over seven weeks is 223.
The median is the middle score for a data set arranged in order of magnitude. The median is less affected by outliers and skewed data.
The formula for the median is as follows:
Find the median number of newspapers sold. (87, 87, 215, 154, 288, 235, 231)
We'll first arrange the data in ascending order.87, 87, 154, 215, 231, 235, 288
The median is the middle term or the average of the middle two terms. The middle two terms are 215 and 231.
Median = (215 + 231)/2
= 446/2
= 223
In statistics, the median measures the central tendency of a set of data. The median of a set of data is the middle score of that set. The value separates the upper 50% from the lower 50%.
Hence, the median number of newspapers sold over seven weeks is 223.
To know more about the median, visit:
brainly.com/question/300591
#SPJ11
The area of a circle is equal to ___ times the ____ of its _____
Answers
Answer:
The area of a circle is equal to pi times the square of its Radius
Step-by-step explanation:
Answer:
Pie, Diameter, Circle
Step-by-step explanation:
i need help fast in these questions.
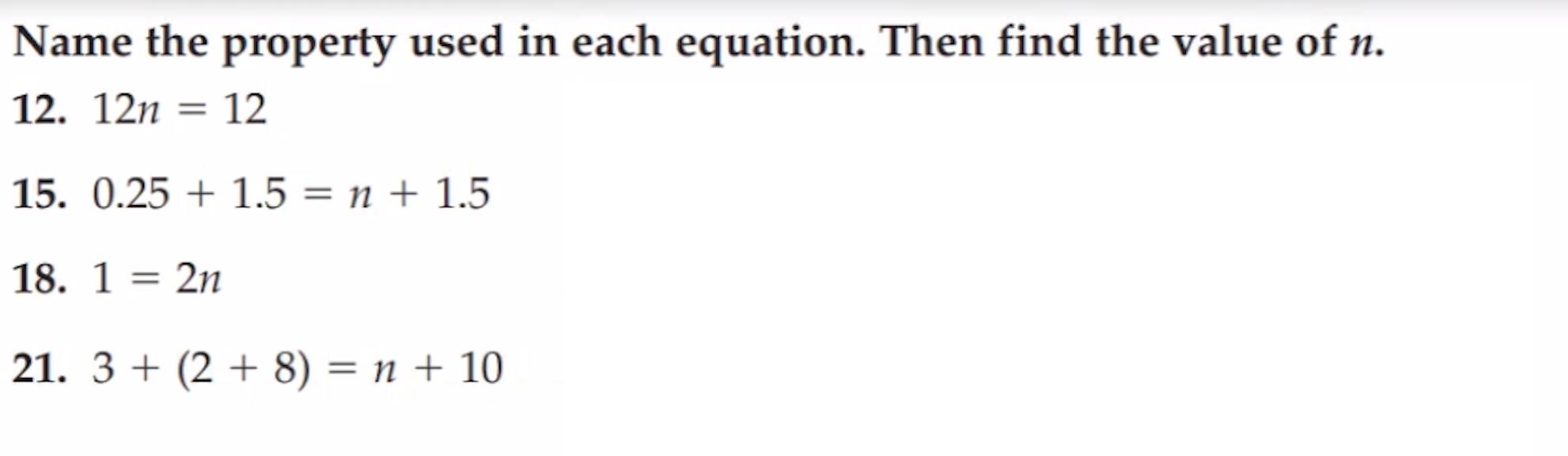
Answers
15. N= 0.25
18. N= 1/2
21. N=3
( i don’t know the properties tho :/ )
Suppose f'(7)=6 and g'(7)=7. Find h'(7) where h(x)=4f(x)+5g(x)+2.
Answers
The derivative of h(x) at x = 7, denoted as h'(7), can be found by applying the sum rule and the constant multiple rule of differentiation. Given that f'(7) = 6 and g'(7) = 7, we can determine that h'(7) = 4f'(7) + 5g'(7) = 4(6) + 5(7) = 24 + 35 = 59.
To find h'(7), we need to differentiate the function h(x) = 4f(x) + 5g(x) + 2 with respect to x. The derivative of a constant term like 2 is zero, so it does not contribute to the derivative of h(x).
Applying the constant multiple rule, we know that the derivative of 4f(x) with respect to x is 4 times the derivative of f(x) with respect to x, and similarly, the derivative of 5g(x) with respect to x is 5 times the derivative of g(x) with respect to x.
Given that f'(7) = 6 and g'(7) = 7, we can substitute these values into the derivative expression for h'(x). Thus, h'(7) = 4f'(7) + 5g'(7) = 4(6) + 5(7) = 24 + 35 = 59. Therefore, at x = 7, the derivative of h(x) is equal to 59.
Learn more about derivative here:
https://brainly.com/question/29020856
#SPJ11
Please help me now! :c

Answers
Answer:
1/64
Step-by-step explanation:
(1/8)² = 1/64
Hey! Could you help me if you can? (Please no links) An 8-ounce serving of pineapples contains 8% of your daily vitamin C. How many ounces of pineapples would you need to get 100% of your daily vitamin C?
Answers
Answer:
100 ounces of pineapples
Step-by-step explanation:
If 8 ounces contains 8%, then 1 ounce contains 1%. 100 ounces = 100%
Answer:
100 ounces
Step-by-step explanation:
8/.08 = c/1
.08c = 1
c = 100
Charlotte is a customer-satisfaction expert at a large pizza company. She took a random sample of 1{,}0001,0001, comma, 000 delivery orders and constructed a one-sample zzz interval to estimate the proportion of delivery orders that take more than an hour to arrive. She decides to repeat this process, but this time she'll use a sample of 4{,}0004,0004, comma, 000 orders. Assume that the point estimates from each sample are approximately equal.What is true about the margins of error from these two samples
Answers
The smaller sample's margin of error will be almost twice as great as the larger sample's margin of error.
Calculating the margin of error for a given sample from a population:
Let the level of significance be and the standard deviation of the population be σ and the sample size be n, then we have:
MOE(Margin of Error)= \(z_{a/2}\times\frac{\sigma}{\sqrt n}\)
Using the above formula to calculate the margin of errors for two specified samples
For first sample:
Sample size = n(1) = 1000
MOE(1) = \(z_{a/2}\times\frac{\sigma}{\sqrt {1000}}\)
For second sample:
Sample size = n(2) = 4000
MOE(2) = \(z_{a/2}\times\frac{\sigma}{\sqrt {4000}}\)
(since it was given that they have same point estimates, so same standard deviation)
Their ratios are given by
MOE(2)/MOE(1) = \(\frac{z_{a/2}\times\frac{\sigma}{\sqrt {4000}}}{z_{a/2}\times\frac{\sigma}{\sqrt {1000}}}\)
MOE(2)/MOE(1) = \(\sqrt{\frac{1000}{4000}}\)
MOE(2)/MOE(1) = 1/2
MOE(1) = 2*MOE(2)
Thus, the margin of error from the smaller sample will be about double of the margin of error from the larger sample.
To learn more about margin of error link is here
brainly.com/question/10501147
#SPJ4
help asap please and thank you!!

Answers
Answer
Solve the following maximisation problem by applying the Kuhn-Tucker theorem: Maxxy 3.6x - 0.4x? + 1.6y - 0.2y?
subject to 2x + y ≤ 10
x ≥ 0
y ≥0
Answers
By applying the Kuhn-Tucker theorem, the maximum value of the given objective function is attained at x = 2.5 and y = 5.
To solve the maximization problem using the Kuhn-Tucker theorem, we follow these steps:
Set up the Lagrangian function: L(x, y, λ) = 3.6x - 0.4x^2 + 1.6y - 0.2y^2 + λ(10 - 2x - y).
Determine the first-order conditions:
∂L/∂x = 3.6 - 0.8x - 2λ = 0
∂L/∂y = 1.6 - 0.4y - λ = 0
Apply the complementary slackness conditions:
λ(2x + y - 10) = 0
λ ≥ 0, x ≥ 0, y ≥ 0
Solve the equations simultaneously to find critical points:
Solve the first-order conditions along with the constraints to obtain x = 2.5, y = 5, and λ = 0.
Check the second-order conditions: Calculate the second derivatives and verify that the Hessian matrix is negative definite.
Evaluate the objective function at the critical point: Substitute x = 2.5 and y = 5 into the objective function to find the maximum value.
Hence, the maximum value of the objective function is attained when x = 2.5 and y = 5.
Learn more about Kuhn-Tucker theorem here: brainly.com/question/32635355
#SPJ11
A brick is lying on a table in a state of static equilibrium. If the mass of the brick is 7. 52 kilograms, what is the normal force exerted by the table on the brick?.
Answers
The normal force exerted by the table on the brick is approximately
73.7 Newtons.
How to determine the normal forceThe weight of the brick can be calculated using the formula:
Weight = mass x acceleration due to gravity
Weight = 7.52 kg x 9.8 m/s²
since the brick is in equilibrium, the normal force exerted by the table on the brick is equal in magnitude but opposite in direction to the weight of the brick.
Therefore, the normal force exerted by the table on the brick is:
Normal force = Weight of the brick
Normal force = 7.52 kg x 9.8 m/s²
Simplifying the calculation:
Normal force ≈ 73.696 N
Learn more about normal force at
https://brainly.com/question/2254109
#SPJ1
Simplify the following expression:
3x - 4y + z- 2z+ x - y
A. 2x - 6z
B. 4x - 5y-z
C. 4x-3y-z
D. 4x - 5y- 3z
Answers
Answer:the answer is b
Step-by-step explanation: 3x+x=4x
-4y-y=-5y
z-2z=-z
Answer:
Answer:the answer is b
Step-by-step explanation: