jamal wants to estimate the
distance across the gorge
shown in the diagram below.
He stands at point Y and
locates a tree at point X
directly across the gorge to the
north. He then walks west
along the gorge 500ft and
marks point A. After walking
another 500ft in the same
direction, he turns 90 degrees
and walks south, perpendicular
to the gorge. He stops when
his location appears to form a
straight line with points A and
X. Jamal measures the
distance BC as 327 ft. What is the distance of XY across the gorge?

Answers
Jamal's estimate of the distance across the gorge is 1424.56 ft
What is Pythagorean Theorem ?
The Pythagorean Theorem is a well-known geometric principle that states that the squares on the hypotenuse of a right triangle, which is the side opposite the right angle, equal the total of the squares on the legs.
First, he can draw a diagram to represent the situation. He can label points Y, X, A, and B on the diagram and draw the lines YX and AB to represent the locations of the tree and the points he marked.
Next, he can use the Pythagorean Theorem to find the distance AC. The theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. In this case, the side AC is the hypotenuse, and the sides YA and YC are the other two sides. Therefore, he can use the theorem to find AC as follows:
AC^2 = YA^2 + YC^2
He knows the values of YA (500ft) and YC (327ft), so he can substitute these values into the equation and solve for AC:
AC^2 = 500^2 + 327^2
AC^2 = 250000 + 107649
AC^2 = 357659
AC = √357659
AC ≈ 597.56 ft
Finally, he can use the distance AC to estimate the distance across the gorge. The distance across the gorge is equal to the distance from X to Y, which is equal to the sum of the distances from X to A and A to Y. Therefore, he can estimate the distance across the gorge as follows:
distance across gorge = XA + AY
distance across gorge = AC + YA + YC
distance across gorge = 597.56 ft + 500 ft + 327 ft
distance across gorge ≈ 1424.56 ft
This is Jamal's estimate of the distance across the gorge.
To learn more about the Pythagoras' theorem from the given link
https://brainly.com/question/343682
#SPJ1
Related Questions
juan needs to make a total of 40 deliveries this week. so far he has completed 18 of them. what percentage of his total delivery has juan completed
Answers
Answer:
45.00%
Step-by-step explanation:
The total answers count 40 - it's 100%, so we to get a 1% value, divide 40 by 100 to get 0.40. Next, calculate the percentage of 18: divide 18 by 1% value (0.40), and you get 45.00% - it's your percentage grade.
Please rate me brainliest
1. Travis makes $459 for 36 hours of work, and Jack makes $535.50 for 42 hours of work.
a. How much do Travis and Jack each make per hour?

Answers
Answer:
Your answers are 12.75 an Hour for both!
Step-by-step explanation:
Really Simple!
459 Dollars / 36 Hours of Labor
= $12.75/ 1 Hour
535.5 Dollars / 42 Hours of Labor
= $12.75/ 1 Hour
When we describe relationships between variables, a correlation nearer to 1.00 (plus or minus) indicates that?
Answers
When we describe relationships between variables, a correlation nearer to 1.00 (plus or minus) indicates the relationship between variables is strong.
The strength and direction of a relationship between two or more variables are described by the statistical measure of correlation, which is given as a number. However, a correlation between two variables does not necessarily imply that a change in one variable is the reason for a change in the values of the other.
When correlation is known, predictions can be made using it. Knowing a score on one measure helps us predict another that is closely related to it more accurately. The forecast will be more accurate the stronger the correlation between/among the variables.
Learn more about correlation here
https://brainly.com/question/4219149
#SPJ4
the base of a pyramid is a rectangle with a length of 7.5 cm and a width of 2 cm. what is the height if the volume is 50 cm^3
Answers
The solution to the given problem of volume comes out to be the pyramid is 10 cm tall.
What does volume actually mean?The volume of a three-dimensional item, which is measured in cubic units, describes how much room it occupies. Liter and in3 are the symbols for cubic measures.
Here,
The formula: gives the volume of a pyramid.
=> V = base_area * height * (1/3)
The area of the base (base_area) of a pyramid whose base is a rectangle with dimensions of 7.5 cm in length and 2 cm in width can be computed as follows:
base_area equals length * width,
=> 7.5 cm * 2 cm =15 cm².
Additionally, we are informed that the pyramid's (V) volume is 50 cm3.
=> (1/3) * 15 * height = 50
=> height = (3 * V)/base_area.
When V and base_area's values are entered, we obtain:
=> height = (15/15) / (3*50) = 10 cm
Consequently, the pyramid is 10 cm tall.
To know more about volume, visit:
brainly.com/question/13338592
#SPJ1
Write an expression for "the quotient of z
and 4.”
Answers
Answer:
z/4 or 4/z i think or z divided by 4
Step-by-step explanation:
Simplify your answer and write it as a proper fraction,improper fraction,or interger
Answers
3-45
∑
n=1
[infinity]
n
2
+2n
2
Answers
The value of the given infinite series of ∑ from n=1 to ∞ of (n²+2)/2 is -3.
We have to evaluate the value of,
∑ from n=1 to ∞ of (n²+2)/2.
This means we need to add up all the terms in the sequence,
Starting with n=1 and going all the way up to infinity.
To do this, we can use a formula for the sum of an infinite series.
We can use the formula for an infinite geometric series, which is:
S = a / (1 - r)
Where S is the sum of the series,
a is the first term,
And r is the common ratio between consecutive terms.
In our case,
The first term is (1²+2)/2 = 1.5, and the common ratio is (n²+2)/2.
We can write this as:
r = (n²+2)/2
Now we need to plug these values into the formula. We get:
S = 1.5 / (1 - (n²+2)/2)
Simplifying this expression, we get:
S = 3 / (4 - n²)
Now we need to evaluate this expression as n approaches infinity.
We can do this by taking the limit as n approaches infinity.
We get:
limit n tends to infinity of S = limit n tends to infinity of (3 / (4 - n²))
Using L'Hopital's rule, we can simplify this expression to:
limit n tends to infinity of S = limit n tends to infinity of (-6n / (2n))
Simplifying further, we get:
limit n tends to infinity of S = limit n tends to infinity of (-3)
Therefore, the sum of the series is -3.
Hence, the value of the given infinite series is -3.
To learn more about sequence visit:
brainly.com/question/12373434
#SPJ4
The complete question is:
Evaluate the value ∑ from n=1 to ∞ of (n²+2)/2.
Melissa obtains a loan for home renovations from a bank that charges simple interest at an annual rate of 16%. Her loan is for $15,400 for 93 days. Assume each day is 365 of a year. Answer each part below. Do not round any intermediate computations, and round your final answers to the nearest cent. If necessary, refer to the list of financial formulas. (a) Find the interest that will be owed after 93 days. XS ? (b) Assurning Melissa doesn't make any payments, find the amount owed after 93 days
Answers
To calculate the interest owed after 93 days, we use the formula for simple interest: Interest = Principal x Rate x Time. Substituting the given values, the interest amounts to $624.49.
This is the total interest that Melissa will owe to the bank after 93 days.Melissa took out a loan of $15,400 from a bank for home renovations. The bank charges a simple interest rate of 16% per year If Melissa doesn't make any payments towards the loan, the total amount owed after 93 days is obtained by adding the principal and the interest together.
Therefore, the total amount owed would be $16,024.49. This means that if Melissa does not make any payments during the 93-day period, her loan balance will increase to approximately $16,024.49, including both the original principal amount and the accrued interest.
To learn more about Interest click here : brainly.com/question/30393144
#SPJ11
Help PLEASE 10pts CMON PEOPLE I NEED TO FINISH THIS TODAY

Answers
because 40+37= 77 and 180-77=104
6. 67
because 41+72=113 and 180-113=67
7. 15
add them together and subtract by 180
8. 44
add together and subtract 180
Use the following statement to answer parts a) and b). Five hundred raffle tickets are sold for $3 each. One prize of $200 is to be awarded. Winners do not have their ticket costs of $3 refunded to them. Raul purchases one ticket.
a) Determine his expected value.
b) Determine the fair price of a ticket.
11. 3#12
Answers
Therefore, the fair price of one raffle ticket is $2.60, which is slightly less than the amount Raul paid ($3).
a) The fair price of one raffle ticket is $3. This is because 500 tickets were sold at this price and one prize of $200 is to be awarded. Therefore, the 500 tickets collected add up to $1,500, while the prize to be awarded is $200. The net amount to be divided among all the ticket holders is $1,300.
b) The fair price of one raffle ticket is $2.60. This is calculated by dividing the total prize money of $200 by the total number of tickets sold (500). Therefore, 500 tickets multiplied by $2.60 gives a total prize money of $1,300 which is equal to the total ticket sales of $1,500 less the prize money of $200.
For more such ticket related questions
https://brainly.com/question/107024
#SPJ11
3x-2(x+5)=14 then x
Answers
3x -2x -10 = 14
x -10 =14
10. 10. add 10 to both sides
x = 24
:)
Answer:
x = 24
Step-by-step explanation:
3x-2(x-5)=14
remove the parentheses using distributive property
3x-2x-10=14
collect like terms
x-10=14
move constant to the right side and change the sign
x=14+10
calculate ( add the numbers together)
x = 24
Find the work W done by a force of 6 pounds acting in the direction 60\deg to the horizontal in moving an object 6 feet from(0,0) to (6,0)
Answers
The work done by the force of 6 pounds acting at an angle of 60 degrees to the horizontal in moving the object 6 feet is 18 foot-pounds.
To find the work done by a force of 6 pounds acting in the direction of 60 degrees to the horizontal in moving an object 6 feet from (0,0) to (6,0), we can use the formula for work:
Work (W) = Force (F) * Distance (d) * cos(θ)
Where:
Force (F) is given as 6 pounds
Distance (d) is the displacement of the object, which is 6 feet in this case
θ is the angle between the force vector and the displacement vector, which is 60 degrees in this case
Plugging in the values into the formula, we have:
W = 6 pounds * 6 feet * cos(60 degrees)
To calculate cos(60 degrees), we need to convert the angle to radians:
60 degrees = (60 * π) / 180 radians
= π / 3 radians
Now we can calculate the work:
W = 6 * 6 * cos(π/3)
Using the value of cos(π/3) = 0.5, we can simplify further:
W = 6 * 6 * 0.5
= 18
To learn more about work done here:
https://brainly.com/question/32305159
#SPJ4
Please help I’m in the middle of a math test and I’m very confused

Answers
Answer:
2
Step-by-step explanation:
in my opinion with out (0,0) there is no others
Write the equation of the line (in slope-intercept form) that has an x-intercept at -6 and a y-intercept at 2. Provide a rough sketch of the line indicating the given points. [1 mark]. Exercise 2. For the polynomial f(x) = −3x² + 6x, determine the following: (A) State the degree and leading coefficient and use it to determine the graph's end behavior. [2 marks]. (B) State the zeros. [2 marks]. (C) State the x- and y-intercepts as points [3 marks]. (C) Determine algebraically whether the polynomial is even, odd, or neither.
Answers
To determine if the polynomial is even, odd, or neither, we substitute -x for x in the polynomial and simplify. -3(-x)² + 6(-x) = -3x² - 6x. Since the polynomial is not equal to its negation, it is neither even nor odd.
To write the equation of the line with an x-intercept at -6 and a y-intercept at 2, we can use the slope-intercept form of a line, y = mx + b, where m is the slope and b is the y-intercept.
In this case, the y-intercept is given as 2, so the equation becomes y = mx + 2. To find the slope, we can use the formula (y2 - y1) / (x2 - x1) with the given points (-6, 0) and (0, 2). We find that the slope is 1/3. Thus, the equation of the line is y = (1/3)x + 2.
For the polynomial f(x) = -3x² + 6x, the degree is 2 and the leading coefficient is -3. The end behavior of the graph is determined by the degree and leading coefficient. Since the leading coefficient is negative, the graph will be "downward" or "concave down" as x approaches positive or negative infinity.
To find the zeros, we set the polynomial equal to zero and solve for x. -3x² + 6x = 0. Factoring out x, we get x(-3x + 6) = 0. This gives us two solutions: x = 0 and x = 2.
The x-intercept is the point where the graph intersects the x-axis, and since it occurs when y = 0, we substitute y = 0 into the polynomial and solve for x. -3x² + 6x = 0. Factoring out x, we get x(-3x + 6) = 0. This gives us two x-intercepts: (0, 0) and (2, 0).
To determine if the polynomial is even, odd, or neither, we substitute -x for x in the polynomial and simplify. -3(-x)² + 6(-x) = -3x² - 6x. Since the polynomial is not equal to its negation, it is neither even nor odd.
Learn more about Polynomial here:
brainly.com/question/28973842
#SPJ11
10x² - 3m - 4
What’s the value of X
Answers
Answer:
it might be 3.8169 to the 6th power or 9.6296 to the 2nd power.
Step-by-step explanation:
but I might be
A financial analyst wants to set up a hypothesis test to determine if the mean yearly salaries of teachers, tutors, and professors are the same. What would be the correct setup for the null and alternative hypotheses for this test
Answers
Null hypothesis (H0): There’s no effect in the population. Alternative hypothesis (Ha or H1): There’s an effect in the population.
Which null and alternative hypotheses are correct?The null and alternative hypotheses are two opposing ideas that researchers use a statistical test to analyze evidence for and against: The null hypothesis (H0) states that there is no influence in the population. Alternative hypothesis (Ha or H1): There is a population effect.
Identify the null and alternative hypotheses.
As well as the sample size, specify.
Choose a suitable statistical test.
Gather information (note that the previous steps should be done prior to collecting data)
Based on the sample data, compute the test statistic.
Examine the null hypothesis, usually indicated by H0.
Always write the alternative hypothesis, which is usually marked by Ha or H1, with less than, greater than, or not equals symbols, i.e., (,>,or).
To learn more about alternative hypotheses to refer:
https://brainly.com/question/28331914
#SPJ4
3. What is Total Surface Area?
4 in
3 in
10 in
O 82
O 140
O 164
O 120

Answers
Answer:
120in. ezy
Step-by-step explanation:
Suppose the random variables X and Y have joint pdf as follows: f(x, y) = 15xy^2, 0 < y < x < 1 Find the marginal pdf f_1 (x) of X. Find the conditional pdf f_2(y | x). Find P(Y > 1/3 | X = x) for any 1/3 < x.< 1 Are X and Y independent?
Answers
The marginal pdf f₁(x) of X is given by f₁(x) = 5x⁴ for 0 < x < 1. The conditional pdf f₂(y | x) = f(x, y) / f₁(x) = (15xy²) / (5x⁴) = 3y² / x³ for 0 < y < x < 1. P(Y > 1/3 | X = x) =2/9x³. X and Y are dependent variables.
The marginal pdf f₁(x) of X can be obtained by integrating the joint pdf f(x, y) over the range of y.
Integrating f(x, y) = 15xy² with respect to y from 0 to x gives:
∫(0 to x) 15xy²
dy = 15x ∫(0 to x) y²
dy = 15x [y³/3] (0 to x)
= 15x (x³/3 - 0)
= 5x⁴.
The conditional pdf f₂(y | x) can be found by dividing the joint pdf f(x, y) by the marginal pdf f₁(x).
So, f₂(y | x) = f(x, y) / f₁(x) = (15xy²) / (5x⁴) = 3y² / x³ for 0 < y < x < 1.
To find P(Y > 1/3 | X = x) for any 1/3 < x < 1,
we integrate the conditional pdf f₂(y | x) with respect to y from 1/3 to 1:
P(Y > 1/3 | X = x)
= ∫(1/3 to 1) (3y² / x³)
dy = 3/x³ ∫(1/3 to 1) y²
dy = 3/x³ [(y³/3)] (1/3 to 1)
= 3/x³ [(1/27) - (1/81)]
= 2/9x³.
To determine if X and Y are independent,
we need to check if f(x, y) = f₁(x) × f₂(y | x).
Given f(x, y) = 15xy² and f₁(x) = 5x⁴,
we can see that f(x, y) ≠ f₁(x) × f₂(y | x). X and Y are dependent variables.
Learn more about integrating here:
https://brainly.com/question/31744185
#SPJ4
someone help me please with this algebra problem
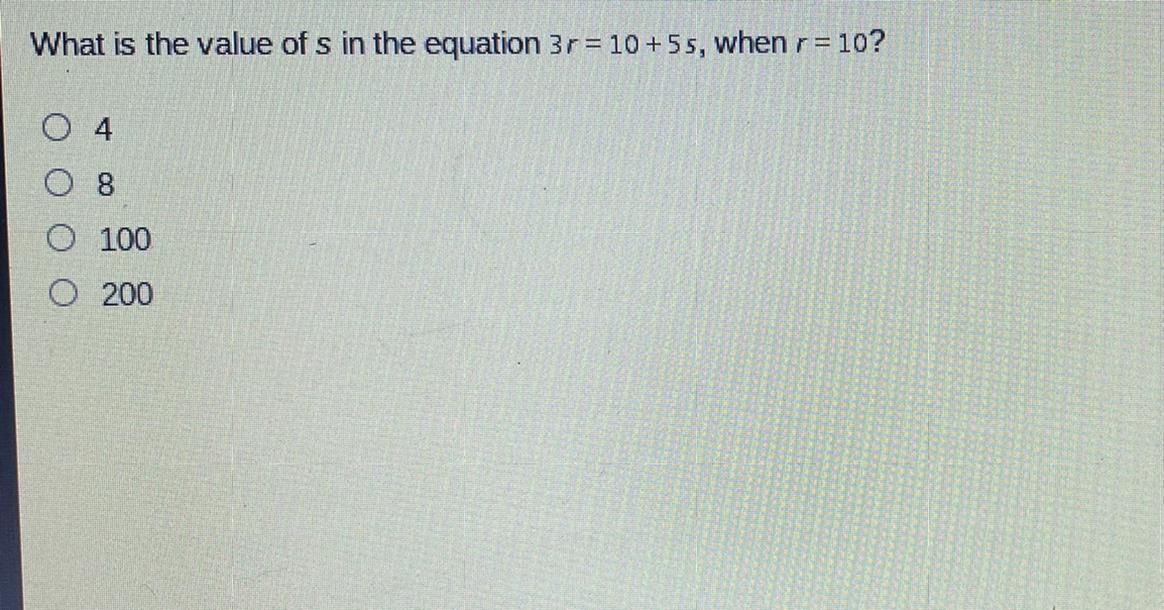
Answers
Answer:
4
Step-by-step explanation:
3r = 10 + 5s
r = 10
3(10) = 10 + 5s
30 = 10 + 5r
20 = 5r
r = 4
Planes S and R both intersect plane T .
Horizontal plane T intersects vertical planes S and R. Planes T and S intersect at line x. Planes T and R intersect and line y. Horizontal line v intersects line x at point B and line y at point A. Line z intersects the lower half of plane S at point C. Point D is on line z but not on a plane.
Which statements are true based on the diagram? Select three options.
Plane S contains points B and E.
The line containing points A and B lies entirely in plane T.
Line v intersects lines x and y at the same point.
Line z intersects plane S at point C.
Planes R and T intersect at line y.

Answers
Answer:
I only know is:planes r and t intersect at line y
Answer:
B- The line containing points A and B lies entirely in plane
C-Line z intersects plane S at point C.
E-Planes R and T intersect at line y.
Step-by-step explanation:
Ed2022
Graph of.... 3 3=0 Y axis Solve the equation oc²³²= 2xx - 3=0 graphically x-20-3=0 Let you² - 2c-3 when y=0 you can find oc OC -2-1 oc² 1 4 4 2244 O O O Scale x axis -3-3-3-3 1 2 345 T 4 9 16 25 -2 -4 -6 -8 -10 -3-3-3-3-3 5/01-310-3 10 15/12
Answers
The solution to the equation does not exist
How to determine the solution to the equationFrom the question, we have the following parameters that can be used in our computation:
2x - 3 = 0
2x - 3 = 3
Also from the question, we understand that the graph is given as
3 = 0
The above equation is false, and cannot be represented on a graph
This is so because 0 and 3 do not have the same value
Similarly, we have 2x - 3 = 0 and 2x - 3 = 3
By substitution, the equations becomes
0 = 3
Hence, the equation has no solution
Read more about equation at
https://brainly.com/question/13729904
#SPJ1
Complete question
Graph of 3=0
Solve the equation 2x - 3 = 0 and 2x - 3 = 3 graphically
I need help with this

Answers
a) Since the triangles are congruent, and ΔABC is congruent to ΔDEF, segments AB and DE have the same value. Therefore, you can use algebra to solve for x when using the knowledge that (12 - 4x) is equal to (15 - 3x).
To solve:
12 - 4x = 15 - 3x
12 = 15 + x
-3 = x
Therefore, x is equal to -3.
b) To find the value of AB, plug in the value of x found in part a).
12 - 4x
12 - 4(-3)
12 - (-12)
12 + 12 = 24
Thus, segment AB is equal to 24.
c) As shown in part b), plug in the value of x found in part a) to find the value of segment DE.
15 - 3x
15 - 3(-3)
15 - (-9)
15 + 9 = 24
Thus, segment DE is also equal to 24.
We can confirm the knowledge of the equal side lengths because the triangle are congruent. This means that all the side lengths in the triangle are the same, which is confirmed when algebraically plugging in the value of x to solve for the values of the segments AB and DE.
I hope this helps!
What transformations produce the graph of g(x)=5^-x+2 from the graph of the parent function f(x)=5^x? Select all that apply.

Answers
Solution
For this case we have the following function:
\(g(x)=5^{-x+2}\)And we want to find the steps to obtain the above function from this one:
\(f(x)=5^x^{}\)So we can do the following:
Reflection over the x axis
horizontal shift to the left 2 units
What is the slope of the line that passes through the points (9,6) and
(5, -8)?
Answers
--------
x2-x1
-8-6
---------
5-9
-14
-----
-4
= 14/4
= 7/2
Revisiting the linear probability model Suppose you are estimating the following linear probability model (LPM): y=β 0
+β 1
x 1
+β 2
x 2
+u where P(y∣x 1
,x 2
)=β 0
+β 1
x 1
+β 2
x 2
and Var(y∣x)=p(x)[1−p(x)] Outline the steps needed to use weighted least squares (WLS) for estimating the LPM. Outline the steps needed to use weighted least squares (WLS) for estimating the LPM. 1. Estimate the model using and obtain the 2. Determine whether all of the are inside the unit interval. If so, proceed to step 3. If not, adjust them so that all values fit inside the unit interval. 3. Construct the estimated variance h i
= 4. Estimate the original model with using weights equal to 1/ h
. True or False: Suppose, for some i, y
^
i
=−2. Although WLS involves multiplying observation i by 1/ h
, the WLS method will be viable without any further adjustments. True False Outline the steps needed to use weighted least squares (WLS) for estimating the LPM. 1. Estimate the model using and obtain the 2. Determine whether all of the are inside the unit interval. If so, proceed to step 3. If not, adjust them so that all values fit inside the unit interval. 3. Construct the estimated variance h i
= 4. Estimate the original model with using weights equal to 1/ h
. True or False: Suppose, for some i, y
^
i
=−2. Although WLS involves multiplying observation i by 1/ h
, the WLS method will be viable without any further adjustments. True False
Answers
WLS involves multiplying observation i by 1/ h_i, the WLS method will be viable without any further adjustments, this statement is True.
To use Weighted Least Squares (WLS) for estimating the Linear Probability Model (LPM) the steps are:
Step 1: Estimate the model using OLS and obtain the residuals, u_i.
Step 2: Determine whether all of the P(y|x1,x2) are inside the unit interval. If so, proceed to step 3. If not, adjust them so that all values fit inside the unit interval.
Step 3: Construct the estimated variance h_i = p(x_i) (1 - p(x_i)).
Step 4: Estimate the original model with weights equal to 1/ h_i.
Thus, the correct answer is True.
Suppose, for some i, y^i = −2.
Although WLS involves multiplying observation i by 1/ h_i, the WLS method will be viable without any further adjustments, this statement is True.
Learn more about WLS method visit:
brainly.com/question/32238993
#SPJ11
a) State the purpose of the presentation, which is to explore the use of tangent lines, tangent planes, and Taylor polynomials for approximate integration. b) Present a graph of the function f(x)=cos 2
x. You may use any program which allows you to produce the graph, but a link to Desmos "Graphing Calculator" has been included in the Moodle Assessment tab for anyone who has never used such a program. c) Present the equation of the tangent line for x=π. d) Present the area under f(x) between x= 2
π
and x= 2
3π
, and compare that to the area under the tangent line at x=π. e) Explain why knowing the area under the tangent line is still useful information in the context of this question. f) Present the equations of T 2
and T 4
, the Taylor polynomials of degree two and degree four centred at x= 2
π
. (Do not expand the polynomials) g) Present a second graph of the function f(x)=cos 2
x, together with the tangent line at x=π. h) Present the numerical values of ∫ 2
π
2
3π
T 2
and ∫ 2
π
2
3π
T 4
, and compare the two values with the actual value of ∫ 2
π
2
3π
cos 2
xdx. (Hint: do not expand the Taylor polynomials to calculate these integrals (calculations that are to be shown in Part 2), instead try to use a certain simple integration technique for easier calculations). i) Comment on the use of polynomial approximations of single-variable functions as a method of approximating integration of single-variable functions. j) Present a graph of the function g(x,y)= x 2
+y 2
2xy
. You may use any program which allows you to produce the graph, but a link to Desmos "Graph a Function of 2 Variables" has been included in the Moodle Assessment tab for anyone who has never used such a program. k) Present the volume between the function and the xy-plane, for R=[0,1]×[0,1]. 1) Present the equation for the plane which is tangent to g(x,y) at the point (1,1). m) Present the volume between the tangent plane and xy-plane, for R=[0,1]×[0,1]. n) Explain why knowing the volume under the tangent plane is still useful information in the context of the question. o) Present the equation of the second-degree Taylor polynomial G(x,y) of g(x,y) at the point (1,1). p) Present a graph of the second-degree Taylor polynomial in o). q) Present the numerical value of the double integral ∬ R
G(x,y)dydx. r) Explain how we know that the level curve g(x,y)=0 exists. s) Explain how the existence of the above level curve influences the accuracy of approximating g(x,y) by its second-degree Taylor polynomial. t) Comment on the use of polynomial approximations of two-variable functions as a method of approximating integration of two-variable functions.
Answers
The purpose of the presentation is to explore the use of tangent lines, tangent planes, and Taylor polynomials for approximate integration. It involves analyzing the function f(x) = \(cos^2(x)\), finding tangent lines and tangent planes.
calculating areas under the curve and the tangent line, examining Taylor polynomials of different degrees, and applying these concepts to a two-variable function \(g(x, y) = (x^2 + y^2)/(2xy).\) The presentation also discusses the importance of knowing the areas and volumes under tangent lines and planes, and the accuracy of polynomial approximations for integration.
The presentation begins by introducing the topic of approximate integration using tangent lines, tangent planes, and Taylor polynomials. It then presents a graph of the function f(x) = \(cos^2(x)\) to visually understand its behavior. The equation of the tangent line at x = π is determined and the area under the curve f(x) and the tangent line between x = 2π/3 and x = 2π is compared. The usefulness of knowing the area under the tangent line is explained.
Next, the equations of the Taylor polynomials T2 and T4, centered at x = 2π, are presented without expanding them. Another graph is shown, depicting the function f(x) = \(cos^2(x)\) along with the tangent line at x = π. The numerical values of the integrals ∫(2π/3 to 2π) T2 and ∫(2π/3 to 2π) T4 are calculated and compared to the actual value of ∫(2π/3 to 2π) \(cos^2(x)dx\).
The use of polynomial approximations for single-variable functions in approximating integration is commented upon. Moving on to two-variable functions, the function g(x, y) = \((x^2 + y^2)/(2xy)\) is graphed. The volume between the function and the xy-plane for the given region R = [0,1]×[0,1] is presented. The equation for the plane tangent to g(x, y) at the point (1,1) is given, followed by the volume between the tangent plane and the xy-plane for the same region.
The usefulness of knowing the volume under the tangent plane is explained in the context of the question. The second-degree Taylor polynomial G(x, y) of g(x, y) at (1,1) is provided, and a graph of the polynomial is shown. The numerical value of the double integral ∬R G(x, y)dydx is computed. The existence of the level curve g(x, y) = 0 is explained and its influence on the accuracy of approximating g(x, y) by its second-degree Taylor polynomial is discussed. Finally, the use of polynomial approximations for two-variable functions in approximating integration is commented upon.
Learn more about Taylor polynomial here
https://brainly.com/question/30481013
#SPJ11
20 points and brainliest answer. Don’t give wrong answers. :)

Answers
Answer:
i is d i think so
Step-by-step explanation:
Answer:
it is A area of trapezoid = 1/2 × h( base1+base2) so it is 1/2× 8×(13+19)
A bookstore sells books at 25% profit calculate the percentage of sales price to cost price ?
Answers
Answer:
Cost price=100%
Step-by-step explanation:
take a square of arbitary measure assuming its area is one square unit.divide it in to four equal parts and shade one of them.again take one shaded part of that square and shade one fourth of it.repeat the same process continuously and find the sum area of shaded region
Answers
Answer:
In recreational mathematics, a square array of numbers, usually positive integers, is called a magic square if the sums of the numbers in each row, each column, and both main diagonals are the same.[1][2] The order of the magic square is the number of integers along one side (n), and the constant sum is called the magic constant. If the array includes just the positive integers {\displaystyle 1,2,...,n^{2}}{\displaystyle 1,2,...,n^{2}}, the magic square is said to be normal. Some authors take magic square to mean normal magic square.[3]
The smallest (and unique up to rotation and reflection) non-trivial case of a magic square, order 3
Magic squares that include repeated entries do not fall under this definition and are referred to as trivial. Some well-known examples, including the Sagrada Família magic square and the Parker square are trivial in this sense. When all the rows and columns but not both diagonals sum to the magic constant we have semimagic squares (sometimes called orthomagic squares).
The mathematical study of magic squares typically deals with its construction, classification, and enumeration. Although completely general methods for producing all the magic squares of all orders do not exist, historically three general techniques have been discovered: by bordering method, by making composite magic squares, and by adding two preliminary squares. There are also more specific strategies like the continuous enumeration method that reproduces specific patterns. Magic squares are generally classified according to their order n as: odd if n is odd, evenly even (also referred to as "doubly even") if n is a multiple of 4, oddly even (also known as "singly even") if n is any other even number. This classification is based on different techniques required to construct odd, evenly even, and oddly even squares. Beside this, depending on further properties, magic squares are also classified as associative magic squares, pandiagonal magic squares, most-perfect magic squares, and so on. More challengingly, attempts have also been made to classify all the magic squares of a given order as transformations of a smaller set of squares. Except for n ≤ 5, the enumeration of higher order magic squares is still an open challenge. The enumeration of most-perfect magic squares of any order was only accomplished in the late 20th century.
Magic squares have a long history, dating back to at least 190 BCE in China. At various times they have acquired occult or mythical significance, and have appeared as symbols in works of art. In modern times they have been generalized a number of ways, including using extra or different constraints, multiplying instead of adding cells, using alternate shapes or more than two dimensions, and replacing numbers with shapes and addition with geometric operations.
The sum area of shaded region is \(\frac{1}{3}\).
Summation formula for geometric progressionThe formula to find the sum of infinite geometric progression is
\(S_{n}=\frac{a_{1}(1-q^{n}) }{1-q} \ \ q \ne 1\)
Given
S = \(\frac{1}{4} +\frac{1}{16} +\frac{1}{64} +.........\)
Using geometric progression
S = \(\lim_{h \to \infty} [\frac{1}{4} +(\frac{1}{4} )^{2} +(\frac{1}{4} )^{3} +.........+(\frac{1}{4} )^{n}]\)
Using summation formula for geometric progression
\(S_{n}=\frac{a_{1}(1-q^{n}) }{1-q} \ \ q \ne 1\)
= \(\lim_{h \to \infty} \frac{\frac{1}{4} (1-(\frac{1}{4} )^{n} }{1-\frac{1}{4} }\)
= \(\lim_{h \to \infty} \frac{\frac{1}{4} (1-\frac{1}{4^{n} }) }{\frac{3}{4} }\)
= \(\lim_{h\to \infty} \frac{1}{3}(1-\frac{1}{4^{n} } )\)
\(\lim_{h\to \infty} \frac{1}{4^{n} }\) = 0
S = \(\frac{1}{3}(1-0) = \frac{1}{3}\)
The sum area of shaded region is \(\frac{1}{3}\).
Find out more information about summation formula for geometric progression here
brainly.com/question/27438806
#SPJ2
The table represents function f,and the graph represents function
Answers
Answer:
The line of symmetry for function f is x = 2 and the line of symmetry for function g is x = 1.
The y-intercept of function f is greater than the y-intercept of function g.
Over the interval [2, 4], the average rate of change of function f is greater than the average rate of change of function g.