Jada walks 12 blocks east and 5 blocks north to get home from school. Jordan, her brother, takes a shortcut and walks northeast through a local park. How many blocks does Jordan walk?Help me please...
Answers
Use the pythagorean theorem to solve for this.
\(c=\sqrt[\square]{a^2+b^2}\)Given:
Jada's track:
a = 12 blocks
b = 5 blocks
Required:
No. of blocks Jordan walked, c = ?
Solution:
\(\begin{gathered} c=\sqrt[\square]{a^2+b^2} \\ c=\sqrt[\square]{12^2+5^2} \\ c=\sqrt[\square]{144+25} \\ c=\sqrt[\square]{169} \\ c=13 \end{gathered}\)Answer: Jordan walked 13 bocks
Related Questions
a casting weighted 148 lb out of the mold. it weighed 141 lb after finishing. what percent of the weight was lost in the finishing?
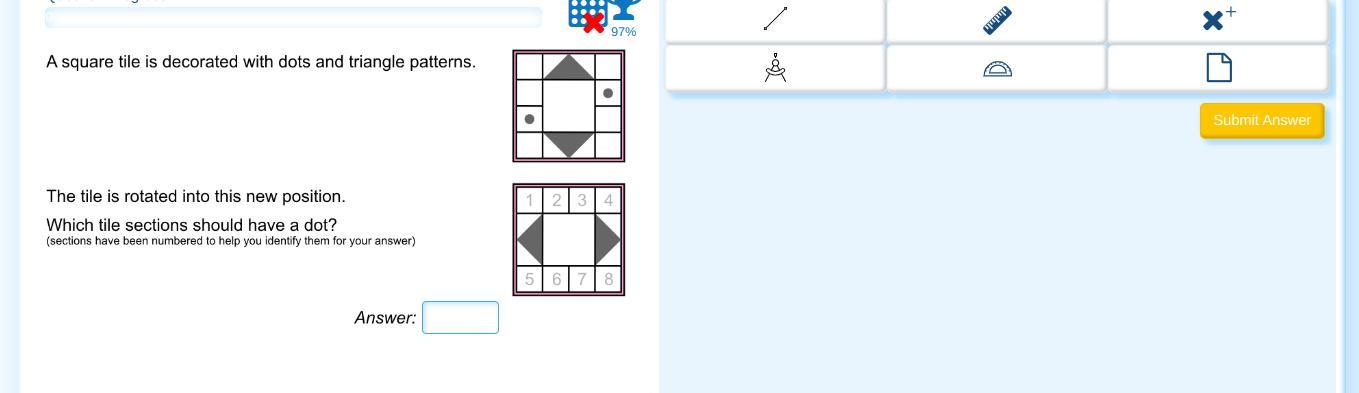
Answers
The amount of weight lost will be equal to 4.72%.
Percentage may be defined as a form of expressing a number as a fraction of hundred. To find the percentage of a number we divide the number by the total amount and then multiply the answer with hundred. The initial weight of the casting was 148 lb and the final weight is 141 lb. To find the percentage we use the formula
Percentage lost = [(Final weight - Initial weight)/Initial weight] × 100
Percentage lost = [(141 - 148)/148] × 100
Percentage lost = ( -7/148) × 100
Percentage lost = -0.0472 × 100
Percentage lost = -4.72% and since we write the absolute value therefore, Percentage lost = 4.72%.
Learn more about percentage at:
brainly.com/question/26352729
#SPJ9
Find the value of the constant that makes the following function continuous on (−∞,∞).
Answers
The piecewise function is continuous only if a = 2.
Which must be the value of the constant a?The function will be continuous if both parts of the function have the same value on the "jump" between the two parts.
The first part evaluated in x = 1 is:
f(x) = (4x^3 - 4x)/(x - 1)
We can rewrite the numerator as:
(4x^3 - 4x) = 4x*(x^2 - 1) = 4x*(x + 1)*(x - 1)
Then we can rewrite the function as:
f(x) = 4x*(x + 1)
Evaluating in x = 1 we will get:
f(1) = 4*1*(1 + 1) = 8
Then the other piece evaluated in x = 1 also must be equal to 8, we will get:
f(x) = 4x^2 + 2x + a
f(1) = 4*1^2 + 2*1 + a = 8
= 4 + 2 + a = 8
a = 8 - 4 - 2 = 2
The value of a must be 2.
Learn more about piecewise functions:
https://brainly.com/question/3628123
#SPJ1
Brainliest for correct answer, any inapplicable answer or absurd answer will be deleted and reported.
Answers
Answer:
65
Step-by-step explanation:
Hi,
Triangles will always add up to 180 degrees. So, 62 + 53 = 115. Subtract it from 180, 180 - 115, and you get 65.
I hope this helps :)
Answer:
65
Step-by-step explanation:
The sum of the three angles of any triangle is equal to 180 degrees
Erika's toy is valued at €450. Its value increased by 10% then decreases by 10% the year after. What is the value of Erika's toy after these two changes?
Answers
Answer:
€445.50-------------------------
Initial value of the toy is €450.
After 10% increase the value is:
€450 + 10% = €450*1.1 = €495After further 10% decrease the value becomes:
€495 - 10% = €495*0.9 = €445.50The final value of the toy is €445.50.
I need Help please!!!
Answers
Step-by-step explanation:
it seems you solved the tricky part yourself already.
just to be sure, let's do the first derivative here again.
the easiest way would be for me to simply multiply the functional expression out and then do a simple derivative action ...
f(t) = (t² + 6t + 7)(3t² + 3) = 3t⁴ + 3t² + 18t³ + 18t + 21t² + 21 =
= 3t⁴ + 18t³ + 24t² + 18t + 21
f'(t) = 12t³ + 54t² + 48t + 18
and now comes the simple part (what was your problem here, don't you know how functions work ? then you are in a completely wrong class doing derivatives; for that you need to understand what functions are, and how they work). we calculate the function result of f'(2).
we simply put the input number (2) at every place of the input variable (t).
so,
f'(2) = 12×2³ + 54×2² + 48×2 + 18 = 96 + 216 + 96 + 18 =
= 426
9. Josie has $30 to spend at a festival. It costs $5 to enter the festival, and the game she wants to play costs $1.40. Write the inequality and use it to determine the number of games (g) that Josie can play.
Answers
She has only $30 with her.
It will cost her $5 to enter the festival and the game she wants to play cost $1.40 .
let
g = number of games
Therefore, the inequality for the number of games she can play can be represented below
\(\begin{gathered} 5+1.40g\leq30 \\ \text{where} \\ g=\text{ number of games she can play} \end{gathered}\)The number of games she can play can be calculated below
\(\begin{gathered} 5+1.40g\leq30 \\ 1.40g\leq30-5 \\ 1.40g\leq25 \\ \text{divide both sides by }1.40 \\ g\leq\frac{25}{1.40} \\ g\leq17.8571428571 \\ g\leq17.86 \\ \text{she can only play approximately 17 games} \end{gathered}\)the correlation between employee iq and productivity in a factory is .12 with a significance of p < .01. what can we conclude
Answers
Answer: There is a small relationship between IQ an productivity.
Step-by-step explanation:
Given: The correlation between employee IQ and productivity in a factory is .12.
Null hypothesis : There is no relationship between employee IQ and productivity.
Alternative hypothesis : There is relationship
between employee IQ and productivity.
Since, p < .01 , where 0.01 is the significance level.
So, we reject the null hypothesis.
That means, there is a relationship between employeeIQ and productivity.
Since correlation coefficient is near to 0, so it represent weak correlation.
Conclusion: There is a small relationship between IQ an productivity.
Which graph is defined by f(x) = x²-x-2|?
O A.
О в.
OC.
O D.
graph A
graph B
graph C
graph D
Answers
For the attached blue bird, find the quadratic equation written in vertex form
Answers
The vertex form of a quadratic equation is expressed as
y = a(x - h)^2 + k
where
h and k are the x and y x and y coordinates of the vertex of the parabola.
a is the leading coefficent
From the information on the graph,
h = 13
k = 13
By substituting these values into the formula,
y = a(x - 13)^2 + 13
On the graph, when x = 26, y = 0
Substituting these values into the equation, we have
0 = a(26 - 13)^2 + 13
0 = a * 13^2 + 13
0 = 169a + 13
169a = - 13
a = - 13/169
a = - 1/13
By substituting a = - 1/13, h = 13 and k = 13 into the verte form equation, the quadratic equation written in vertex form is
y = - 1/13(x - 13)^2 + 13
The point A has coordinates (-1, 6) and the point B has coordinates (7, 2).
i Find the equation of the perpendicular bisector of AB, giving your answer in the form y = mx + c.
ii A point C on the perpendicular bisector has coordinates (p, q). The distance OC is 2 units, where O is
the origin. Write down two equations involving p and q and hence find the coordinates of the possible
positions of C.
Answers
Answer:
a) y = 2x -2
b) Equation: q = 2p - 2 ----(1)
p² + q² = 4 ----(2)
The coordinates of C may be (0, -2) or (6/5, 8/5)
Step-by-step explanation:
a) Step 1: Find the coordinates of midpoint, P of AB
x-co-ordinate of P = (x₁ + x₂)/2 = (-1 + 7)/2 = 3
y- co-ordinate of P = (y₁ + y₂)/2 = (6 + 2)/2 = 4
Step 2: Determine the gradient, m₂ of perpendicular bisector of AB
For perpendicular lines, m₁ * m₂ = -1 where m₁ is slope of AB
m₁ = (2 - 6)/(7 - -1) = -4/8 = -1/2
-1/2 * m₂ = -1
m₂ = 2
Step 3: Deriving the equation of the perpendicular bisector in the form y = mx + c
y - y₁ = m(x - x₁); substituting the values of the midpoints of the line
y - 4 = 2(x - 3)
y - 4 = 2x - 6
y = 2x -2
b) Step 1: Derive the values of the p and using the formula of distance between two points:
y = 2x - 2
therefore q = 2p - 2 ----(1)
OC = √(x₂ -x₁)² + (y₂ - y₁)²
2 = √(p - 0)² + ( q - 0)²
2 = √p² + q²
squaring both sides
p² + q² = 4 ----(2)
Substituting (1) in (2)
p² + (2p - 2)² = 4
p² + 4p² - 8p + 4 = 4
5p² - 8p = 0
p(5p - 8) = 0
Therefore p = 0 or 5p - 8 = 0
p = 0 or p = 8/5
Substituting p = 0 in (1)
q = -2
substituting p = 8/5 in (1)
q = 2(8/5) - 2
q = 16/5 - 2
q = 6/5
Hence the coordinates of C may be (0, -2) or (6/5, 8/5)
A portfolio manager generates a 5% return in Year 1, a 12% return in Year 2, a negative 6% return in Year 3, and a return of 2% (nonannualized) in the first quarter in Year 4. The annualized return for the entire period is the closest to __________.
Answers
The annualized return for the entire period is the closest to 10.5%.
To calculate the annualized return for the entire period, we need to consider the returns for each year and the return in the first quarter of Year 4. Since the returns are given for each period, we can use the geometric mean to calculate the annualized return.
The formula for calculating the geometric mean return is:
Geometric Mean Return = [(1 + R1) * (1 + R2) * (1 + R3) * (1 + R4)]^(1/n) - 1
Where R1, R2, R3, and R4 are the returns for each respective period, and n is the number of periods.
Given the returns:
Year 1 return: 5% or 0.05
Year 2 return: 12% or 0.12
Year 3 return: -6% or -0.06
First quarter of Year 4 return: 2% or 0.02
Using the formula, we can calculate the annualized return:
Annualized Return = [(1 + 0.05) * (1 + 0.12) * (1 - 0.06) * (1 + 0.02)]^(1/3) - 1
Annualized Return = (1.05 * 1.12 * 0.94 * 1.02)^(1/3) - 1
Annualized Return = 1.121485^(1/3) - 1
Annualized Return ≈ 0.105 or 10.5%
Therefore, the annualized return for the entire period is approximately 10.5%.
For more question on return visit:
https://brainly.com/question/30761579
#SPJ8
Find x-intercept of the line
4x +11y=20
Answers
Answer:
x=5
Step-by-step explanation:
Answer:
5
Step-by-step explanation:
Desmos Graphing Calculator
\(57=\frac{5}{8}z+7\)
Answers
\(57=\cfrac{5}{8}z+7\implies 57=\cfrac{5z}{8}+7\implies \stackrel{\textit{multiplying both sides by }\stackrel{LCD}{8}}{8(57)=8\left( \cfrac{5z}{8}+7 \right)} \\\\\\ 456=5z+56\implies 400=5z\implies \cfrac{400}{5}=z\implies 80=z\)
There are three containers: a 10 liter container, a 7 liter container, and a 4 liter container. The 7 and 4 liter containers are initially full of water, while the 10 liter container is empty. There is only one operation: pour the contents of one container into the other stopping only when the pouring container is empty or the receiving container is full. • Is there a sequence of pourings that leaves exactly 2 liters in the 4 liter container? • Model this as a graph problem: Define the graph. What is the problem that needs to be solved? What algorithm can be used to solve this problem?
Answers
One algorithm that can be used to solve this problem is the breadth-first search algorithm. This algorithm explores all the possible pourings from the initial state, and then all the possible pourings from those states, and so on, until the desired state is reached.
Yes, there is a sequence of pourings that leaves exactly 2 liters in the 4 liter container. The sequence of pourings is as follows:
1. Pour the 7 liter container into the 10 liter container. The 7 liter container is now empty and the 10 liter container has 7 liters of water.
2. Pour the 4 liter container into the 10 liter container. The 4 liter container is now empty and the 10 liter container has 11 liters of water.
3. Pour the 10 liter container into the 7 liter container until the 7 liter container is full. The 10 liter container now has 4 liters of water and the 7 liter container is full.
4. Pour the 7 liter container into the 4 liter container until the 4 liter container is full. The 7 liter container now has 3 liters of water and the 4 liter container is full.
5. Pour the 4 liter container into the 10 liter container. The 4 liter container is now empty and the 10 liter container has 8 liters of water.
6. Pour the 7 liter container into the 4 liter container. The 7 liter container is now empty and the 4 liter container has 3 liters of water.
7. Pour the 10 liter container into the 7 liter container until the 7 liter container is full. The 10 liter container now has 1 liter of water and the 7 liter container is full.
8. Pour the 7 liter container into the 4 liter container until the 4 liter container is full. The 7 liter container now has 2 liters of water and the 4 liter container is full.
9. Pour the 4 liter container into the 10 liter container. The 4 liter container is now empty and the 10 liter container has 9 liters of water.
10. Pour the 7 liter container into the 4 liter container. The 7 liter container is now empty and the 4 liter container has 2 liters of water.
To model this as a graph problem, we can define the graph as follows:
- Each vertex represents a state of the containers, with the amount of water in each container as the vertex label.
- Each edge represents a pouring operation, with the label indicating which container is being poured into which container.
The problem that needs to be solved is finding a path from the initial state to the desired state, where the 4 liter container has 2 liters of water.
One algorithm that can be used to solve this problem is the breadth-first search algorithm. This algorithm explores all the possible pourings from the initial state, and then all the possible pourings from those states, and so on, until the desired state is reached.
Learn more about Algorithm
brainly.com/question/22984934
#SPJ11
10-² =
Exponential form
Answers
Copy the base to the right side of the equality
10-^2=10
Rewrite the exponent -2 as the product of (-1) and 2
10-^2=10^(-1)x2
First, use the Power of a Power Property
10-^2=(10^(-1) ) ^2
Any number raised to the power of can be written as its reciprocal
10^-2=(1/10)^2
Next, use the Power of a Quotient Property
10^-2=1^2/10^2
1 raised to any power equals 1
10^-2=1/10^2
so the answer is 10^-2=1/10^2
Answer:
Step-by-step explanation:
the answer is 0.01
The base of the exponential form is 10 and the power is -2 therefore the answer is 0.01 if the power was 2 the answer would have been 100
to learn more visit the link below
https://brainly.com/question/27804970?referrer=searchResults
(5n²+7)+(-2n-4). Add
Answers
Answer:
Step-by-step explanation: Refer to attachment.
Which methods correctly solve for the variable x in the equation 7-x=18
Answers
Answer:
x = -11
Step-by-step explanation:
7 - x = 18
+ x on both sides to cancel the negative one
7 = 18 + x
- 18 on both sides to get rid of the 18
solve:
7 - 18 = x
-11 = x
Answer:
collecting like terms
Step-by-step explanation:
step 1. Shift 7 to the right side
-x = 18 - 7
-x = 11
step 2. divide by -1 both sides
-x/-1 = 11/-1
x = -11
Line k is represented by the equation y = 2x + 2. Write
an equation of a line that is perpendicular to line k that also passes through the point (-2, 9)?
Answers
Step-by-step explanation:
so, we calculate the perpendicular slope, and then we start with the point-slope form (since we were given a specific point of the line), and transform into the regular slope-intercept form.
the slope in
y = 2x + 2
is the factor of x : 2 or 2/1
the perpendicular slope is turning this upside down and flips the sign : -1/2
the point- slope form is
y - y1 = a(x - x1)
"a" being the slope, (x1, y1) being the point.
y - 9 = -1/2(x - -2)
y - 9 = (-1/2)x - 1
y = (-1/2)x + 8
5x⁵x⁸(3.141593)
Solve!!!
Answers
Answer:
=15.707963x¹³
Step-by-step explanation:
=5*x⁵*x⁸*3.141593
=15.707963*x¹³
=15.707963x¹³
Note:
(*) sign means the sign of multiplication (×)
\(\\ \rm\Rrightarrow 5x^5x^8(3.141593)\)
\(\\ \rm\Rrightarrow 5x^{5+8}(3.141593)\)
\(\\ \rm\Rrightarrow 5x^{13}(3.141593)\)
\(\\ \rm\Rrightarrow 15.7x^{13}\)
Please answer this correctly
Answers
Answer:
The second graph.
Step-by-step explanation:
0-9: 6 numbers
10-19: 2 numbers
20-29: 1 number
30-39: 3 numbers
40-49: 1 number
50-59: 2 numbers
60-69: 0 numbers
70-79: 5 numbers
80-89: 3 numbers
90-99: 1 number
18) Solve for side AC.
A) 1.10
B) 8.24
C) 9.50
70
C
3
B
Answers
Step-by-step explanation:
tan0=opp/adj
where opposite =3,adjacent =x,=70
tan 70=3/x
2.7474=3/x
2.7474x=3
divide both sides by 2.7474
x=3/2.7474
x=1.0919
x=1.10 to 1 d.p
I need help on this please! Thanks
Answers
Answer:
B. The product of 5 and a number.
Product means multiplication is taking place. In this case, 5 is being multiplied with n.
Hope this helps!
please help quick giving 25 points
Answers
Answer:
Step-by-step explanation: 5.) Circular shape.
6.) Feet.
7.) Circle.
8.) The circumference is 9 and the radius is 18.
9.) By the way we would need to use The Circumference as 2 and the radius to be 9 to equal 18 for the radius circle.
Here please helppppppppppppp
Answers
Answer:
Part 2 - ∠EGF = 105° Part 3 - ∠D = 65________________________________________________Step-by-step explanation for Part-2:
We know that:
∠EFG = 32°∠AEG = 137°∠EFG + ∠FGE + ∠GEF = 180°Work:
∠EFG + ∠FGE + ∠GEF = 180°32 + ∠FGE + (180 - 137) = 180°=> 32 + ∠FGE + 43 = 180°=> 75 + ∠FGE = 180°=> ∠FGE = 180 - 75=> ∠FGE = ∠EGF = 105°Hence, the measure of ∠EGF is 105°.
________________________________________________Step-by-step explanation for Part-3:
We know that:
CD = CAThis triangle is an isosceles triangle.∠D = ∠AWork:
50 + ∠D + ∠A = 180=> ∠D + ∠D = 130=> 2∠D = 130=> ∠D = 130/2=> ∠D = 65Hence, the measure of ∠D is 65°
________________________________________________What is the x-intercept for function f?
f(x) = −23x + 8
Answers
The x-intercept for function f(x) = −23x + 8 is (8/23, 0)
In this question, we have been given a function f(x) = −23x + 8
We need to find the x-intercept for given function f(x)
Let f(x) = y
So, given function becomes,
y = −23x + 8
To find the x-intercept, set y = 0,
0 = -23x + 8
23x = 8
x = 8/23
Therefore, the x-intercept for function f(x) = −23x + 8 is (8/23, 0)
Learn more about x-intercept here:
https://brainly.com/question/14180189
#SPJ1
You are curious whether or not the following two events meet the standard criteria in statistics for mutually exclusive events:
January sales exceeding $1 million
February sales exceeding $1 million
Which of the following conditions alone would guarantee that those two events are mutually exclusive?
a. Sales each month are statistically independent of each other.
b. Sales each month are not statistically independent of each other.
c. Available inventory prevents sales for January and February combined from exceeding $1.5 million.
d. In any given month the probability of sales exceeding $1 million is less than 50%. The expected sales in January is more than the expected sales in February.
e. None of the above.
Answers
Answer:
d. In any given month the probability of sales exceeding $1 million is less than 50%. The expected sales in January is more than the expected sales in February.
Step-by-step explanation:
The above condition about the probability of sales exceeding $1 MILLION BEING LESS THAN 50% would guarantee that.
Jessica needs to know how much water her new fish tank can hold:
A rectangular prism with a length of 8 inches, a width of 4 inches, and a height of 9 inches.
Determine the total volume of the fish tank.
Answers
The fish tank has a total volume of 288 inch³. As a result, Jessica's new fish tank has a capacity of 288 inch³ for water.
The volume of a rectangular prism can be calculated using the formula:
V = l x b x h..........(i)
where,
V ⇒ Volume
l ⇒ length
b ⇒ width
h ⇒ height
From the question, we are given the values,
l = 8 inches
b = 4 inches
h = 9 inches
Putting these values in equation (i), we get,
V = 8 x 4 x 9
⇒ V = 288 in³
Therefore, the fish tank has a total volume of 288 inch³. As a result, Jessica's new fish tank has a capacity of 288 inch³ for water.
Learn more about the volume of rectangular prism on:
https://brainly.com/question/24284033
Rotation - Question 5
Answers
When the former image is rotated, the dots will be located at section 2 and 7.
What is the effects of image rotation?When an image is rotated, the constituents within it also changes its position as the object is moves from a point to another about a pivot junction.
From the given image above, after the rotation of the initial image, the dot should be located at number 2 and 7 of the new image.
Learn more about rotation here:
https://brainly.com/question/30337265
#SPJ1
- On an arcade game, Connor got the 100-point bonus 5 times and the 150-point penalty 3 times. If he started with 200 points, how many points does he have now? Explain how you found your answer.
Answers
Answer: 1,150
Step-by-step explanation:
100 x 5 = 500
150 x 3 = 450
500 + 450 + 200
Connor has 1,150 points
Please help
Of 104 athletes surveyed about what
sport they play, some play basketball.
Of those that play basketball, 32 play
soccer and the remaining 29 do not
play soccer. Write an equation to find
the number of athletes surveyed who
do not play basketball. Let n represent
the number of athletes surveyed who
do not play basketball.
Answers
Step-by-step explanation:
n = 104 - (32 + 29)
32 and 29 (playing soccer or not) are the basketball players. that is 61 together.
so, the number of surveyed non-basketball players is then the rest of the 104 :
104 - 61 = 43