It took Todd 11 hours to travel over pack ice from one town in the Arctic to another town 330 miles away. During the return journey, it took him 15 hours.
Assume the pack ice was drifting at a constant rate, and that Todd’s snowmobile was traveling at a constant speed relative to the pack ice.
What was the speed of Todd's snowmobile?
Answers
Answer:
The speed of Todd's snowmobile was 22 miles an hour
Step-by-step explanation:
:))
The speed of Todd's automobile is 31 miles per hour.
What is speed?Speed is defined as the ratio of the time distance travelled by the body to the time taken by the body to cover the distance. Speed is the ratio of the distance travelled by time. The unit of speed in miles per hour.
Given that It took Todd 11 hours to travel over pack ice from one town in the Arctic to another town 330 miles away. During the return journey, it took him 15 hours.
For the first journey,
v₁ + v₂ = 330 / 11 ......................( 1 )
For the return journey,
v₂ - v₁ = 330 / 15 .........................( 2 )
From equation ( 1 ) and equation ( 2 ),
2v₂ = ( 330 / 11 ) + ( 330 / 15 )
2v₂ = ( 330 ) ( 31 / 165 )
v₂ = 165 ( 31 / 165 )
v₂ = 31 miles per hour
To know more about speed follow
https://brainly.com/question/27384390
#SPJ2
Related Questions
54 divided by u = 9.
Answers
Answer:
6 = u
Step-by-step explanation:
54 / u = 9
We have to isolate "u" all by itself;
54 = 9*u
54 / 9 = u
6 = u
Hope this helps!
Answer:
6
Step-by-step explanation:
We need to find of u value such that , 54 divided by u = 9. Converting it into equation ,
Equation :-
→ 54/u = 9
→ 1/u = 9 × 1/54
→ 1/u = 1/6
→ u = 6
Hence the required answer is 6.The equation y=1/5x+3.5 can be used to find the amount of accumulated snow y in inches x hours after 5 P.M. on a certain day. Graph this equation.
Answers
The coordinates of the y-intercept are (0, 3.5) and the coordinates of the x-intercepts are (-17.5, 0). Using these coordinates, the graph of the equation is shown below.
Graphing linear equationsFrom the question, we are to graph the given linear equation.
To graph the equation,
We will determine the coordinates of the x-intercepts and y-intercepts.
When x = 0
y = 1/5x + 3.5
y = 1/5(0) + 3.5
y = 3.5
(0, 3.5)
When y = 0
y = 1/5x + 3.5
0 = 1/5x + 3.5
Multiply through by 5
0 = x + 17.5
x = -17.5
(-17.5, 0)
Using the coordinates of the x-axis and y-axis, the graph of the equation is shown below.
Learn more on Graphing linear equations here: https://brainly.com/question/11860022
#SPJ1

answer quick for brainliest

Answers
Therefore, P(K|J) is equal to 1/5 in its simplest form.
What is fraction?
A fraction is a mathematical expression that represents a part of a whole. It is written in the form of one integer (the numerator) divided by another integer (the denominator), separated by a horizontal line. For example, the fraction 2/5 represents two parts out of a total of five parts.
The numerator represents the number of parts we are interested in, while the denominator represents the total number of equal parts that make up the whole. Fractions can be proper (the numerator is less than the denominator), improper (the numerator is greater than or equal to the denominator), or mixed (a whole number and a fraction together). Fractions are used in a wide range of mathematical operations, such as addition, subtraction, multiplication, and division.
by the question.
We can use the formula P(B/A) = P(B∩A)/P(A) to calculate P(KJ), where A is the event that J occurs, and B is the event that K and J occur.
First, we need to find P(K|J∩N). We can use the formula P(JNK) = P(KJ∩N)/P(J) to find this value.
\(P(K|J∩N) = P(JNK) * P(J) = (1/5) * (3/7) = 3/35\)
Next, we need to find P(J) = 3/7.
Finally, we can use the formula P(K|J) = P(K|J∩N)/P(J) to find P(KJ):
\(P(K|J) = P(KJ∩N)/P(J) = (3/35) / (3/7) = (3/35) * (7/3) = 1/5\)
To learn more about fraction:
https://brainly.com/question/10708469
#SPJ1
36.
A meeting started at 11.35a.m. and
ended at 4.15p.m the same day. How
long did the meeting last?
a) 3hrs 40mins
b) 3hrs 50mins
c) 4hrs 35mins
d) 4hrs 40mins
e) 5hrs 40mins
What’s the answer
Answers
Answer:
Step-by-step explanation:
option (d) 4hrs 40mins
Which two points on the number line represent numbers that can be combined to make zero?

Answers
Answer:
B and D I think.............
Answer:
B and D
Step-by-step explanation:
Pls help I need help on this question

Answers
Answer: B
Step-by-step explanation: Hope this helps:)
The data manager for a state political party gathered data to determine how many citizens would support the party’s senate candidate. He polled citizens in 30 similarly sized senate districts and found a sample mean of 70,438 citizens. Statewide data shows that the population standard deviation is 645.3. What is the approximate 90% confidence interval for this situation?
Answers
The approximate 90% confidence interval for this situation is given as follows:
(70244, 70632).
What is a z-distribution confidence interval?The bounds of the confidence interval are given by the rule presented as follows:
\(\overline{x} \pm z\frac{\sigma}{\sqrt{n}}\)
In which:
\(\overline{x}\) is the sample mean.z is the critical value.n is the sample size.\(\sigma\) is the standard deviation for the population.From the z-table, the critical value for a 95% confidence interval is given as follows:
z = 1.645.
The parameters are given as follows:
\(\overline{x} = 70438, \sigma = 645.3, n = 30\)
The lower bound of the interval is given as follows:
\(70438 - 1.645 \times \frac{645.3}{\sqrt{30}} = 70244\)
The upper bound of the interval is given as follows:
\(70438 + 1.645 \times \frac{645.3}{\sqrt{30}} = 70632\)
More can be learned about the z-distribution at https://brainly.com/question/25890103
#SPJ1
Use the following information for questions 10 and 11.
Helena uses the following equations to model the profit for her business, where a represents months:
Last year's profit:
-0.3x1 + 843 - 70.3x2 + 247.5x - 137.7
This year's anticipated profit:
0.243 - 3.7x2 + 36.1x + 48.2
10. Which polynomial models the total profit, in dollars, for both last year and this year?
A. 0.1x1 + 4.3x3 - 34.2x2 + 295.7x
- 137.7
B. -0.1x1 + 4.3,3 - 34.2x2 + 295.72
- 137.7
C. -0.324 + 8.23 - 74x2 + 283.6x
- 89.5
D. 0.324 + 8.2,3 - 74x2 + 283.6x
- 89.5
11. Which polynomial models how much more profit Helena anticipates this year compared to what she made last year?
A. 0.5x4 - 11.723 + 106.422 + 199.3x
+ 137.7
B. 0.1x4 - 4.3x3 + 34.222 - 199.3
- 137.7
C. -0.3x4 + 7.843 + 66.6x2 + 211.4x
+ 89.5
D. 0.3x4 - 7.8x3 + 66.6x2 - 211.4x
+ 185.9
Answers
10) Total revenue is 0.1x¹ + 4.3x³ - 34.2x² + 295.7x - 137.7. 11) Profit for this year minus profit for last year equals 0.3x⁴ - 7.8x³ + 66.6x² - 211.4x + 185.9.
What is profit?Profit is the financial gain that is achieved when the revenue from sales or business activities exceeds the expenses, costs, and taxes associated with running the business or conducting those activities.
According to question:10) To find the polynomial that models the total profit for both last year and this year, we add the two given profit equations:
Last year's profit: -0.3x¹ + 843 - 70.3x² + 247.5x - 137.7
This year's anticipated profit: 0.243 - 3.7x² + 36.1x + 48.2
Total profit = Last year's profit + This year's anticipated profit:
Total profit = (-0.3x¹ + 843 - 70.3x² + 247.5x - 137.7) + (0.243 - 3.7x² + 36.1x + 48.2)
Simplifying and combining like terms, we get:
Total profit = -0.3x¹ + 36.1x - 74x² + 295.7
Therefore, the polynomial that models the total profit for both last year and this year is:
A. 0.1x¹ + 4.3x³ - 34.2x² + 295.7x - 137.7
11) To find the polynomial that models how much more profit Helena anticipates this year compared to what she made last year, we can subtract the equation for last year's profit from the equation for this year's anticipated profit:
This year's anticipated profit: 0.243 - 3.7x² + 36.1x + 48.2
Last year's profit: -0.3x + 843 - 70.3x² + 247.5x - 137.7
Difference in profit = This year's anticipated profit - Last year's profit:
Difference in profit = (0.243 - 3.7x² + 36.1x + 48.2) - (-0.3x¹ + 843 - 70.3x² + 247.5x - 137.7)
Simplifying and combining like terms, we get:
Difference in profit = 0.3x¹ - 3.7x² + 36.1x - 595.5
Therefore, the polynomial that models how much more profit Helena anticipates this year compared to what she made last year is:
D. 0.3x⁴ - 7.8x³ + 66.6x² - 211.4x + 185.9
To know more about profit visit:
https://brainly.com/question/22474377
#SPJ1
If sin x=0.96, find tan x
Answers
Step-by-step explanation:
sin x= P/H
sin x = 0.96 = 96/100 = 24/25.
Let the ratio of the sides be x.
B²=H²-P²
B²=(25x)²-(24x)²
B²=625x²-576x²
B²=49x²
B=√49x²
B= 7x.
cos x = 7x/25x = 7/25.
therefore, tan x = sin x / cos x = (24/25)/(7/25) = 24/25×25/7 = 24/7 .
hope this helps you.
Halona walks 1.93 kilometers to a neighbor's house in 23 minutes. Assuming she walks at a constant speed, write a proportion that represents how many kilometers, y, Halona can walk in z minutes. Then solve your proportion for y. 1.93 Proportion: у х 23 y =
Answers
EXPLANATION:
The proportion states that he walks 1.93 kilometers at a constant speed in 23 minutes, so we can formulate the equation in the same way:
-First we must divide to find the constant or the proportion, then we divide 1.93 by 23; we represent the constant with the letter k:
\(\begin{gathered} K=\frac{y}{x} \\ k=\frac{1.93}{23} \\ k=0.08 \\ \text{ANSWER:} \\ \text{The constant or porportion is :0.083} \end{gathered}\)With the constant found we can propose an equation that determines the constant speed at which Halona walks at any time.
Now we can formulate the following equation:
\(\begin{gathered} y=(z)(k) \\ y=(z)(0.08) \\ where\text{ z is }any\text{ moment of time; an k is the }cons\tan t\text{ value} \end{gathered}\)Multiplying any time with the constant will give us the constant speed.
IMPORTANT NOTE:
When we give different values to time, it must be multiplied by the constant, which means that the speed remains stable.
What pair of numbers have a greatest common factor of 7?
Answers
Answer:
answers are:
7 and 14
The factors of 7 is: 1, 7
The factors of 14 is: 1, 2, 7, 14
28 and 7
Factors of 28: 1, 2, 4, 7, 14, 28
Facotrs of 7: 1, 7
Step-by-step explanation:
others:
21, 3 is GCF is 3
The factors of 3 are: 1, 3
The factors of 21 are: 1, 3, 7, 21
7, 1 is GCF is 1
The factors of 1 are: 1
The factors of 7 are: 1, 7
Boxes of raisins are labeled as containing 22 ounces. Following are the weights, in the ounces, of a sample of 12 boxes. It is reasonable to assume that the population is approximately normal.
21.88 21.76 22.14 21.63 21.81 22.12 21.97 21.57 21.75 21.96 22.20 21.80
Required:
Construct a 90% confidence interval for the mean weight.
Answers
Answer:
A 90% confidence interval for the mean weight is [21.78 ounces, 21.98 ounces].
Step-by-step explanation:
We are given the weights, in the ounces, of a sample of 12 boxes below;
Weights (X): 21.88, 21.76, 22.14, 21.63, 21.81, 22.12, 21.97, 21.57, 21.75, 21.96, 22.20, 21.80.
Firstly, the pivotal quantity for finding the confidence interval for the population mean is given by;
P.Q. = \(\frac{\bar X-\mu}{\frac{s}{\sqrt{n} } }\) ~ \(t_n_-_1\)
where, \(\bar X\) = sample mean weight = \(\frac{\sum X}{n}\) = 21.88 ounces
s = sample standard deviation = \(\sqrt{\frac{\sum (X-\bar X)^{2} }{n-1} }\) = 0.201 ounces
n = sample of boxes = 12
\(\mu\) = population mean weight
Here for constructing a 90% confidence interval we have used a One-sample t-test statistics because we don't know about population standard deviation.
So, 90% confidence interval for the population mean, \(\mu\) is ;
P(-1.796 < \(t_1_1\) < 1.796) = 0.90 {As the critical value of t at 11 degrees of
freedom are -1.796 & 1.796 with P = 5%}
P(-1.796 < \(\frac{\bar X-\mu}{\frac{s}{\sqrt{n} } }\) < 1.796) = 0.90
P( \(-1.796 \times {\frac{s}{\sqrt{n} } }\) < \({\bar X-\mu}\) < \(1.796 \times {\frac{s}{\sqrt{n} } }\) ) = 0.90
P( \(\bar X-1.796 \times {\frac{s}{\sqrt{n} } }\) < \(\mu\) < \(\bar X+1.796 \times {\frac{s}{\sqrt{n} } }\) ) = 0.90
90% confidence interval for \(\mu\) = [ \(\bar X-1.796 \times {\frac{s}{\sqrt{n} } }\) , \(\bar X+1.796 \times {\frac{s}{\sqrt{n} } }\) ]
= [ \(21.88-1.796 \times {\frac{0.201}{\sqrt{12} } }\) , \(21.88+1.796 \times {\frac{0.201}{\sqrt{12} } }\) ]
= [21.78, 21.98]
Therefore, a 90% confidence interval for the mean weight is [21.78 ounces, 21.98 ounces].
How much time, in seconds, did the vehicle in this diagram spend STOPPED?

Answers
Answer:
like 10 i think
Step-by-step explanation:
the flat line is the time it spends stopped im pretty sure so that would be 10 seconds
-6(1+7x)+7(1+6x)=-2
Answers
-6(1+7x)+7(1+6x)=-2
This is False.
Use distributive property:
-6 -42x + 7 +42x = -2
Combine like terms to get:
1 = -2
Since 1 is not -2, it is false.
Graph the line with the equation y = – 1/5x-3
Answers
Answer:
Check image
Step-by-step explanation:

Jimmy ate 1/3 of his sandwich at lunch. He ate another 2/3 of the sandwich. How much of the sandwich did Jimmy eat in all?
A.1/3
B.2/3
C.3/3
D.5/3
Answers
How do I answer this?

Answers
Answer:
Step-by-step explanation:
area of trapezium ABCD
=(16.5+12)/2 \times 15
=(28.5)/2 \times 15
=213.75 cm^2
\(\frac{PQ}{DC} =\frac{8}{12} =\frac{2}{3}\)
Area of PQRS
=213.75 \times (\frac{2}{3} )^2\\=213.75 \times\frac{4}{9} \\=95 ~cm^2
area of green portion=213.75-95=118.75 cm²
Find the sum of the measures of the interior angles of the figure.

Answers
Answer:
\(\huge\boxed{\sf 900}\)
Step-by-step explanation:
Sides of the figure = n = 7
Formula for measuring the interior angles of a polygon:(n - 2)×180
Where n is the number of sides in the polygon
So,
Measure of interior angles in the figure:= (n - 2) × 180
= (7 - 2) × 180
= 5 × 180
= 900
\(\rule[225]{225}{2}\)
Answer: 720°
Step-by-step explanation:
- Assuming this is a regular hexagon, all the sides are equal and all the angles are equal
- One of the properties of a regular hexagon is that the sum of all the interior angles is 720°
- Since the sum of all the interior angles is 720°, this means each interior angle is 120°
hope this helps :)
i still dont get rounding multiplication
Answers
An electrician charges y amount to work x hours on a job. The electrician charges a $50 service fee and $30 per hour. His income per job can be modeled using a linear function. The electrician works maximum of 20 hours on any job. What is the range of values for one job?
Answers
Answer:
The range of values from one job is between $50 and $650.
Step-by-step explanation:
An electrician charges y amount to work x hours on a job. The electrician charges a $50 service fee and $30 per hour.
This means that his earnings in a job can be modeled by the following function:
\(y = 30x + 50\)
The electrician works maximum of 20 hours on any job. What is the range of values for one job?
Minimum, he works 0 hours, and earns:
\(y(0) = 30(0) + 50 = 50\)
Maximum, he works 20 hours, and earns:
\(y(20) = 30(20) + 50 = 650\)
The range of values from one job is between $50 and $650.
Someone help what would be the evaluation of this?

Answers
help pls!!!!!
What is the inequality for this verbal description?
The value of y is greater than or equal to the sum of five times the value of x
and negative three.

Answers
Answer:
y ≥ 5x+ (-3)
Step-by-step explanation:
greater than or equal to ≥
The sum means add
y ≥ 5x+ (-3)
Answer:
Option D, y ≥ 5x + (-3)
Step-by-step explanation:
Step 1: Make an expression
The value of y is greater than or equal to the sum of five times the value of x and negative three.
The value of y is greater than or equal to ← y ≥
The sum of five times the value of x and negative three ← 5x + (-3)
y ≥ 5x + (-3)
Answer: Option D, y ≥ 5x + (-3)
How to solve -10 divided by 0.22.
Answers
Answer:
-45.4545455
Step-by-step explanation:
you would do like you would do with a regular division problem accept you take the negative out and you don't put until last bcuz whatever answer you get is gonna be a negative number. You would also move the decimal place of .22 back by two times so that the decimal place would be behind the number altogether and it becomes 22 and you would also add 2 zeros behind the negative 10 and get 1000.
Now just divide 1000 by 22 and get your answer and put the negative sign back. I know the way I explained it is weird, but that's cuz I'm not used to having to explain.
What is the value of (4-2)3-3x4

Answers
Parenthesis is 2, cubed is 8
Multiply, gives you 12
8-12 = -4
Answer:
The answer is -4.
Step-by-step explanation:
It is -4 using the method of PEMDAS. Subtract 4 and 2 together in the parentheses to get 2. Multiply to the third root power to get 8. Then, multiply -3 by 4 together to get -12. Finally, subtract 12 from 8 to get -4 as your final answer.
divide a line of 1.8m into three parts in the ratio of 5:7:8
Answers
Answer:
0.45 m, 0.63 m, 0.72 m
Step-by-step explanation:
Let the three parts of the line be 5x, 7x and 8x
Therefore,
5x + 7x + 8x = 1.8
20x = 1.8
x = 1.8/20
x = 0.09
5x = 5*0.09 = 0.45 m
7x = 7*0.09 = 0.63 m
8x = 8*0.09 = 0.72 m
HELP IM IN K12 AND THERS MORE OF THESE

Answers
2/0 = 32/48 = 30/0. What number shpuld come in place of the zeros?
Answers
Answer:
\(\sf \dfrac{2}{3} = \dfrac{32}{48} = \dfrac{30}{45}\)
For the 1st part\(\sf \rightarrow \dfrac{2}{x} = \dfrac{32}{48}\)
\(\sf \rightarrow 2(48)= {32x}\)
\(\sf \rightarrow 32x= 96\)
\(\sf \rightarrow x = 3\)
For the 2nd part\(\rightarrow \sf \dfrac{32}{48} = \dfrac{30}{y}\)
\(\rightarrow \sf {32y} = 30(48)\)
\(\rightarrow \sf {32y} = 1440\)
\(\rightarrow \sf y = 45\)
Function and notaion.

Answers
Answer: 45
Step-by-step explanation:
Function notation: is another way of writing a function to make it easy to understandInstead of the independent and dependent variables being x and y they are now x and f(x)f(x) can be interpreted as the y value at a given x value in this case f(-5) must be solved for, essentially saying what is y when the x value is -5\(f(-5)=2(-5)^{2} -5\)
\(f(-5)= 2(25) -5\)
\(f(-5) = 50-5\)
\(f(-5) = 45\)
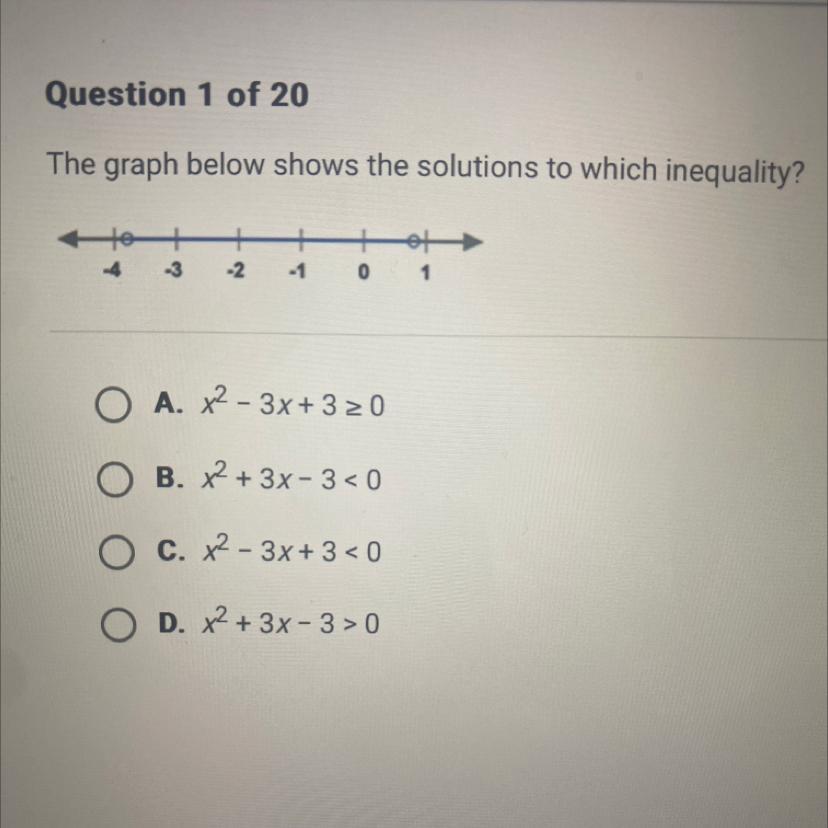
The graph below shows the solutions to which inequality?
A. x^2-3x+3 ≥0
B. x² + 3x-3 <0
C. x²-3x+3<0
D. x² + 3x-3>0
Answers
The inequality expression that corresponds to the solution of the inequality graph is x² + 3x - 3 < 0.
option B.
What is the solution of the inequality?The inequality expression that corresponds to the solution of the inequality graph is determined by simplifying the equations as follows;
The solution of the graph,
x > -4 and x < 1
The first equation with "≥" is ruled out because the graph doesn't have a thick dot.
Let's simplify the second expression;
x² + 3x - 3 < 0
solve using quadratic formula;
x > -3.79 or x < 0.79
The third expression is ruled out since its solution will be complex.
For the last expression;
x² + 3x - 3 > 0
x < -3.79 or x > 0.79
Thus, the correct inequality expression is x² + 3x - 3 < 0.
Learn more about inequality expression here: https://brainly.com/question/25275758
#SPJ1
i really need actual help on this asap

Answers
On the bisector place a point F
Join F to both D and E to form the triangle