it took oliva 2 hour to drive 240 miles. at this rate how long does it take to drive 80 miles
Answers
Answer:
40 minutes
Step-by-step explanation:
rate = distance/time = miles/hr
rate = 240 mi/2 hr = 120 mi/hr
time = distance / rate = (80 mi)/(120 mi/hr) = 0.67 hr = 40 minutes
(0.67 hr)(60 min/hr) = 40 minutes
Related Questions
Someone pls help ASAP!!!!

Answers
calculate the molecular weight of a gas with a density of 1.524 g/l at stp.
Answers
To calculate the molecular weight of a gas with a density of 1.524 g/l at STP, we can use the ideal gas law: PV = nRT. At STP, the pressure (P) is 1 atm, the volume (V) is 22.4 L/mol, and the temperature (T) is 273 K. The molecular weight of the gas with a density of 1.524 g/L at STP is approximately 32.0 g/mol.
Rearranging the equation, we get n = PV/RT.
Next, we can calculate the number of moles (n) of the gas using the given density of 1.524 g/l. We know that 1 mole of any gas at STP occupies 22.4 L, so the density can be converted to mass by multiplying by the molar mass (M) and dividing by the volume: density = (M*n)/V. Rearranging the equation, we get M = (density * V) / n.
Substituting the given values, we get n = (1 atm * 22.4 L/mol) / (0.0821 L*atm/mol*K * 273 K) = 1 mol. Then, M = (1.524 g/L * 22.4 L/mol) / 1 mol = 34.10 g/mol. Therefore, the molecular weight of the gas is 34.10 g/mol.
To calculate the molecular weight of a gas with a density of 1.524 g/L at STP, you can follow these steps:
1. Recall the ideal gas equation: PV = nRT
2. At STP (Standard Temperature and Pressure), the temperature (T) is 273.15 K and the pressure (P) is 1 atm (101.325 kPa).
3. Convert the density (given as 1.524 g/L) to mass per volume (m/V) by dividing it by the molar volume at STP (22.4 L/mol). This will give you the number of moles (n) per volume (V):
n/V = (1.524 g/L) / (22.4 L/mol)
4. Calculate the molar mass (M) of the gas using the rearranged ideal gas equation, where R is the gas constant (8.314 J/mol K):
M = (n/V) * (RT/P)
5. Substitute the values and solve for M:
M = (1.524 g/L / 22.4 L/mol) * ((8.314 J/mol K * 273.15 K) / 101325 Pa)
6. Calculate the molecular weight of the gas:
M ≈ 32.0 g/mol
Therefore, the molecular weight of the gas with a density of 1.524 g/L at STP is approximately 32.0 g/mol.
Learn more about molecular weight at: brainly.com/question/27988184
#SPJ11
2. Call a number prime-looking if it is composite but not divisible by 2, 3, or 5. The three smallest prime-looking numbers are 49, 77, and 91. There are 168 prime numbers less than 1000. How many prime-looking numbers are there less than 1000
Answers
There are 225 prime-looking numbers less than 1000. To determine this, we need to find composite numbers that are not divisible by 2, 3, or 5.
We know that there are 168 prime numbers less than 1000. To find the prime-looking numbers, we can subtract the number of prime numbers from the total number of composite numbers less than 1000.
There are a total of 999 - 168 = 831 composite numbers less than 1000.
Next, we need to remove the composite numbers that are divisible by 2, 3, or 5.
Out of the 831 composite numbers, we can identify those divisible by 2, 3, or 5 by checking their last digit. If the last digit is 0, 2, 4, 5, 6, or 8, the number is divisible by 2 or 5. If the sum of its digits is divisible by 3, the number is divisible by 3. By removing these numbers, we can find prime-looking numbers.
After performing these calculations, we find that there are 225 prime-looking numbers less than 1000.
Learn more about prime numbers here:
https://brainly.com/question/29629042
#SPJ11
find an equation of the tangent line to the curve xe^y + ye^x = 2 at the point (0, 2).
Answers
Therefore, the equation of the tangent line to the curve xe^y + ye^x = 2 at the point (0, 2) is y = -x + 2.
To find an equation of the tangent line to the curve xe^y + ye^x = 2 at the point (0, 2), we need to use the concept of differentiation.
First, we differentiate both sides of the equation with respect to x using the product rule and the chain rule:
(d/dx)[xe^y] + (d/dx)[ye^x] = (d/dx)[2]
e^y + xe^y(dy/dx) + e^x(dy/dx) + ye^x = 0
Simplifying this expression and evaluating it at the point (0, 2), where x = 0 and y = 1, we get:
e^1 + 0 + e^0(dy/dx) + 2e^0 = 0
dy/dx = -1
Therefore, the slope of the tangent line at the point (0, 2) is -1.
Next, we can use the point-slope form of a line to find the equation of the tangent line. We know the slope is -1 and the point (0, 2) lies on the line, so we can write:
y - 2 = -1(x - 0)
Simplifying this expression, we get:
y = -x + 2
To know more about tangent line,
https://brainly.com/question/28089413
#SPJ11
Please help!! I will mark brainliest for first correct!!
Find the length of a using
the Pythagorean Theorem.
B
8
a
С.
A
6
Hint: a2 + b2 = c2
Round your answer to the nearest tenth.
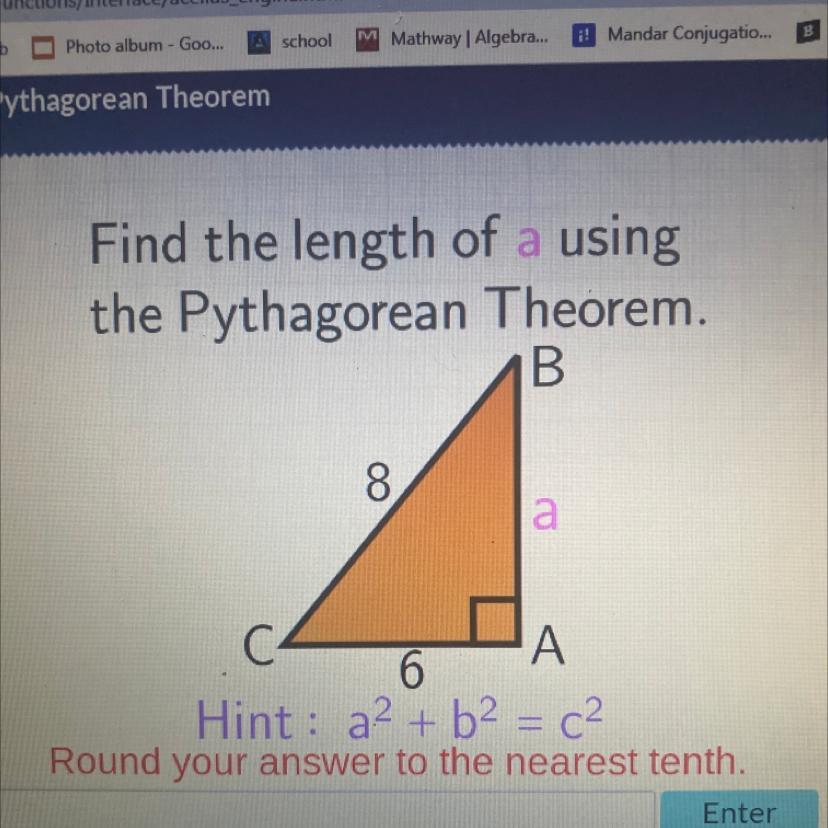
Answers
Answer:
5.3 is the answer rounded to the nearest 10th
Which lines best approximate the directrices of the ellipse? Round to the nearest tenth. X = −4. 6 and x = 4. 6 x = −3. 5 and x = 3. 5 y = −4. 6 and y = 4. 6 y = −3. 5 and y = 3. 5
Answers
The lines best approximate the directrices of the ellipse y = 10.6 or y = -6.6
The term called directrices of the ellipse is defined as a line parallel to the latus rectum of ellipse and is perpendicular to the major axis of the ellipse.
Here we know that first of all here the known form is an ellipse with a vertical major axis so it would have to be
=> d = a²/c
Here d refers the distance between the center and the directrix.
When we take the value of a= 8, b=3, then we get the value of C as,
=> c² = a²- b²
Apply the value on it, then we get
=> c ² = 64-9
Then the value of is about 7.4
Then the value of d is calculated as,
=> d = 64/7.4 = 8.6
So the value of y is defined as,
=> 2 + 8.6 = 10.6
Or if it falls the negative direction, then we get
=> y = 2 - 8.6 = -6.6
To know more about directrix here.
https://brainly.com/question/17376399
#SPJ4
If robert reads 2pages per minute, how many pages could she read in 1 1/2 hours?
Answers
Robert can read 180 pages in \(1\frac 12\) hours
How to determine the number of pages?The given parameters in the question are:
Speed = 2 pages per minute
Number of hours = \(1\frac 12\) hours
The number of pages to read in this time can be calculated using the following equation
Number of pages = Speed * Number of hours
Substitute the known values in the above equation So, we have the following equation
Number of pages = 2 * \(1\frac 12\)
Convert the units
Number of pages = 2 * \(1\frac 12\) * 60
Evaluate
Number of pages = 180
Hence, the number of pages is 180 pages
Read more about unit rates at
https://brainly.com/question/19493296
#SPJ1
solve the following using the annihlator method. i. y′′ 3y′ 2y = 5 ln(x)
Answers
The solution to the given differential equation is y(x) = (x^2)(A + B ln(x)) - (5/8)x^2 + Cx + D, where A, B, C, and D are constants.
To solve the differential equation y'' + 3y' + 2y = 5 ln(x), we use the annihilator method.
First, we find the annihilator of the function ln(x), which is (D^2 - 1)y, where D represents the differentiation operator. Multiplying both sides of the equation by this annihilator, we have (D^2 - 1)(y'' + 3y' + 2y) = (D^2 - 1)(5 ln(x)).
Expanding and simplifying, we get D^4y + 2D^3y + D^2y - y'' - 3y' - 2y = 5D^2 ln(x).
Rearranging, we have D^4y + 2D^3y + D^2y - y'' - 3y' - 2y = 5D^2 ln(x).
Now, we solve this fourth-order linear homogeneous differential equation. The general solution will have four arbitrary constants. To find the particular solution, we integrate 5 ln(x) with respect to D^2.
Integrating, we obtain -5/8 x^2 + Cx + D, where C and D are integration constants.
Therefore, the general solution to the given differential equation is y(x) = (x^2)(A + B ln(x)) - (5/8)x^2 + Cx + D, where A, B, C, and D are constants.
Learn more about differentiation operator here:
https://brainly.com/question/32069063
#SPJ11
4. using the data from problem 3, create a 95 percent confidence interval for the ratio of the variances. please use 1 decimal place in your answer. at the 95 percent confidence level, is there a difference in the population variances of the two processes? please justify your answer.
Answers
For the population variance the confidence interval of 95% with standard deviation s = 17 is equal to (176.22, 559.35).
Sample standard deviation s = 17
sample size 'n' = 25
population variance= o2
To construct a confidence interval for the population variance,
Use the chi-square distribution,
The formula for the confidence interval is,
((n-1) × s^2)/chi2(a/2, n-1) ≤ o^2 ≤ ((n-1) × s^2)/chi2(1-a/2, n-1)
where chi-square(a/2, n-1) and chi-square(1-a/2, n-1) are the chi-square values for the given significance level a and degrees of freedom (n-1).
Substituting the given values, we get,
((25-1) × 17^2)/chi2(0.025, 24) ≤ o^2 ≤ ((25-1) × 17^2)/chi2(0.975, 24)
Calculating the chi-square values using a chi-square distribution attached table ,we get,
((24) × 17^2)/39.36 ≤ o^2 ≤ ((24) ×17^2)/12.40
Simplifying the expressions, we get,
176.22 ≤ o^2 ≤ 559.35
Therefore, the 95% confidence interval for the population variance is (176.22, 559.35).
learn more about population variance here
brainly.com/question/14880145
#SPJ4
The given question is incomplete, I answer the question in general according to my knowledge:
Construct a 95% confidence interval for the population variance o2 if a sample of size 25 has standard deviation s = 17. Round the answers to two decimal places. The 95% confidence interval

25] 26. Find the volume of the region that is between the ry-plane and f(x, y) = y + e** and above the triangle with the vertices (0,0), (2,0) and (2, 2). [7 marks]
Answers
The volume of the region that is between the ry-plane and
f(x, y) = y + e^x
= 4 - 3e^2.
and above the triangle with the vertices (0,0), (2,0), and (2, 2)
The region can be visualized in the following diagram:
Volume of the region between the ry-plane and
f(x, y) = y + e^x
and above the triangle can be calculated using the following double integral:
∬T (f(x, y) - 0) dA,
where T is the triangle with vertices (0,0), (2,0), and (2, 2).
Using the above integral we get:
∫02 ∫0yx + e^ydydx + ∫22 ∫0(2 - x + e^y) dydx,
this becomes equal to
∫02 ∫0yx + e^ydydx + ∫22 [y* (2 - x) + e^y(2 - x) - e^y] dydx.
Integrating with respect to y we get,
∫02 ∫0yx + e^ydydx + ∫22 [y^2/2 + e^y(2 - x) - e^y * y]
limits from y = 0 to
y = x dx + ∫22 [y^2/2 + e^y(2 - x) - e^y * y]
limits from
y = x to y = 2
dx= ∫02 ∫0x + e^ydydx + ∫22 [(2 - x) * (2 - x)/2 + e^x(2 - x) - e^x * x - x^2/2 - e^x * x + e^x * 2] dx.
Solving the integral we get:
∫02 ∫0x + e^ydydx + ∫22 [- x^2/2 + 2xe^x - (5/2)e^x + 2] dx
= ∫02 [(x + xe^x - (5/2)e^x + 2x^2/2)]
limits from x = 0 to x = 2
dx = [(2 + 2e^2 - 5e^2 + 2*2^2/2)] - [(0 + 0 - 0 + 2*0^2/2)]
= 2 + 2e^2 - 5e^2 + 2
= 4 - 3e^2.
Thus, the volume of the region is 4 - 3e^2.
Hence, the required volume is 4 - 3e^2.
To know more about vertices visit:
https://brainly.com/question/29154919
#SPJ11
PLEASE ANSWER THIS ASAP I WILL MARK YOU THE BRAINLIEST
SHOW YOUR WORK!!!
Calculate the volume of the following three-dimensional object

Answers
Area of cyclinder:
Area at base x height
Pi = 3.142
5^2 x 3.142 = 78.55
78.55 x 4 = 314.2
What is an equation of the line that passes through the points ( 3 , 1 ) and ( − 3 , − 7 ) ?
Answers
Answer:
y = 4/3x - 3
Step-by-step explanation:
Use this formula to find the slope first.
(y2 - y1) / (x2 - x1)
(x2, y2) --> (-3, -7)
(x1, y1) ---> (3, 1)
Now plug in:
(-7 - 1) / (-3 - 3) = -8 / -6 = 4/3
Now find the y intercept by plugging any points to y= 4/3x + b
I will use (3, 1).
1 = 4/3(3) + b
1 = 4 + b (subtract 4 on both sides)
-3 = b
So the formula is
y = 4/3x - 3
Barbara sells iced tea for $1. 49 per bottle and water for $1. 25 per bottle. She wrote an equation to find the number of bottles she needs to sell to earn $100. 1. 25x 1. 49 = 100 What error did Barbara make in writing the equation? Barbara’s equation did not consider the number of bottles of water. Barbara’s equation did not consider the number of bottles of iced tea. Barbara’s equation did not use the correct price for the bottles of iced tea. Barbara's equation did not use the correct total for sales.
Answers
The correct option is The Barbara equation did not consider the number of bottles of water.
Given,
The selling price of iced tea is $1.49 per bottle.
The selling price of water is $1.25 per bottle.
Equation written by the Barbara,
\(1.25x+1.49=100\)
Here in this question Barbara multiply the selling price of bottle with the number of bottle using the coefficient x, But she did not use any coefficient for the bottle of water. The correct equation is,
\(1.25x+1.49y=100\)
where y is the number of water bottle sold to earn the profit of $100.
Hence the correct option is the Barbara equation did not consider the number of bottles of water.
For more about the linear equation, follow the link below-
https://brainly.com/question/11897796
Susie mixed 6 cups of popcorn with 2 cups of pretzels. She then divided the snack into bags with cup in each. After dividing, how many bags of snack bags will Susie have?
Answers
Answer:
5 points and enough....
Answer:
8 bags
Step-by-step explanation:
all you have to do is 6+2 divied by how may cups there are
A ball on a pendulum moves 30 cm on its first swing. Each succeeding swing it
moves 0.5 the distance of the previous swing. What is the total distance that the
ball moves before coming to rest? Write your answer in the box.
Answers
Answer:
130cm
Step-by-step explanation:
Completely factor the polynomial. 12x2 2x - 4 2(3 x 2)(2 x - 1) (3 x 2)(4 x - 2) 2(6 x2 2 x - 1) (6 x 4)(2 x - 1)
Answers
The completely factored form of the polynomial is :\(\(12x^2 + 2x - 4 = 2(2x + 4)(3x - 1)\)\)
To completely factor the polynomial \(\(12x^2 + 2x - 4\)\), we need to find expressions that can be multiplied together to obtain the given polynomial.
First, we can look for common factors. In this case, all the coefficients are divisible by 2, so we can factor out a 2:
\(\(2(6x^2 + x - 2)\)\)
Now, we focus on factoring the quadratic expression \(\(6x^2 + x - 2\)\). We need to find two binomials that, when multiplied, give us this quadratic.
To factor \(\(6x^2 + x - 2\)\), we look for two numbers whose product is equal to \(\(6 \times -2 = -12\)\) and whose sum is equal to the coefficient of the middle term, which is 1.
After trying different combinations, we find that the numbers 4 and -3 satisfy these conditions:
\(\(6x^2 + x - 2 = (2x + 4)(3x - 1)\)\)
Putting it all together, the completely factored form of the polynomial is:
\(\(12x^2 + 2x - 4 = 2(2x + 4)(3x - 1)\)\)
To know more about polynomial visit -
brainly.com/question/32838567
#SPJ11
Write a linear equation for the line that goes through point (5,7) and has a slope of 3.

Answers
ANSWER
y = 3x - 8
EXPLANATION
The equation of a line is:
\(y=mx+b\)where m is the slope and b is the y-intercept.
In this problem we know that the slope is m = 3. To find the y-intercept we have to replace x and y by the point and solve for b:
\(\begin{gathered} y=3x+b \\ 7=3\cdot5+b \\ 7=15+b \\ b=7-15 \\ b=-8 \end{gathered}\)Therefore, the equation is:
\(y=3x-8\)plz answer number 6 (ITS NOT A)

Answers
Answer:
b
Step-by-step explanation:
Answer:
I think C
Step-by-step explanation:
can someone help me out please

Answers
what is a indirect proportion?
Answers
Answer:
Indirect or inverse proportion is a relation between two quantities where an increase in one leads to a decrease in the other, and vice-versa. It is just the opposite of direct proportion.
Step-by-step explanation:
Giving brainlist for this question. Please quick I am falling behind thanks.

Answers
Answer:
3x
Step-by-step explanation:
5x - 3x + 2x - x
2x + 2x - x
4x - x
3x
Hope this helps!
kelly sold 35 books at £1.40 each. 28 bracelets at £1.50 each. some badges at 80p each. She got a total of £115. Work out how many badges Kelly sold
Answers
Answer:
the answer is 30 !! :)
Step-by-step explanation:
115-(35*1.40)-(28*1.50)= 24
24/.8 = 30
A student said that X +1 is written in simplest form is the student correct explain why or why not
Answers
No, the student is not correct. X + 1 is a polynomial expression in its simplest form since it cannot be factored or simplified further. The expression does not contain any like terms that can be combined and there are no common factors to be factored out. Therefore, X + 1 is already in its simplest form.
X+1 is a polynomial expression in its simplest form since it cannot be factored or simplified further. In general, an expression is in its simplest form when it is fully simplified and cannot be reduced any further using any of the rules of algebra. In the case of "X+1," the expression has only two terms, and it is not possible to combine them any further. Therefore, "X+1" is already in its simplest form.
It's important to note that the term "simplest form" typically applies to fractions or radicals, not polynomial expressions. For example, a fraction like 4/8 can be simplified to 1/2, and a radical expression like the square root of 8 can be simplified to 2 times the square root of 2. However, polynomial expressions like "X+1" cannot be further simplified as they are already in their simplest form.
Learn more about polynomial here: brainly.com/question/20121808
#SPJ11
(Two-Step Linear Inequalities MC) Which graph represents the solution to the inequality 2(b + 2) > 24? number line with open point at 10 with arrow pointing left number line with closed point at 10 with arrow pointing left number line with closed point at 10 with arrow pointing right number line with open point at 10 with arrow pointing right
Answers
The graph that represents the solution to the inequality is a number line with closed point at 10 with arrow pointing left
What is a graph?You should be aware that inequality is is a mathematical statement showing that two opposite things are not equal. The graph is a diagram that illustrates the statement.
The given inequality is 2(b + 2) > 24
Opening the brackets to get
2b+4≥24
2b≥24-4
This implies that 2b≥20
Making b the subject
b≥20/2
b≥10
Therefore, the graph is a number line with closed point at 10 with arrow pointing left
Learn more about inequality on https://brainly.com/question/28823603
#SPJ1
Solve each equation. 4 y-6=2 y+8
Answers
The solution of the linear equation in one variable 4y - 6 = 2y + 8 is at y = 7.
According to the given question.
We have a linear equation in one variable.
4y - 6 = 2y + 8
As we know that, the linear equations in one variable is an equation which is expressed in the form of ax+b = 0, where a and b are two integers, and x is a variable and has only one solution.
Thereofre, the solution of the linear equation in one variable 4y - 6 = 2y + 8 is given by
4y - 6 = 2y + 8
⇒ 4y - 2y - 6 = 8 ( subtracting 2y from both the sides)
⇒ 2y -6 -8 = 0 (subtracting 8 from both the sides)
⇒ 2y - 14 = 0
⇒ 2y = 14
⇒ y = 14/2
⇒ y = 7
Hence, the solution of the linear equation in one variable 4y - 6 = 2y + 8 is at y = 7.
Find out more information about equation here:
https://brainly.com/question/28583552
#SPJ4
A fair coin is tossed 5 times. Calculate the probability that (a) five heads are obtained (b) four heads are obtained (c) one head is obtained A fair die is thrown eight times. Calculate the probability that (a) a 6 occurs six times (b) a 6 never happens (c) an odd number of 6s is thrown.
Answers
To calculate the probabilities, we need to use the concept of binomial probability.
For a fair coin being tossed 5 times:
(a) Probability of getting five heads:
The probability of getting a head in a single toss is 1/2.
Since each toss is independent, we multiply the probabilities together.
P(Head) = 1/2
P(Tails) = 1/2
P(Five Heads) = P(Head) * P(Head) * P(Head) * P(Head) * P(Head) = \((1/2)^5\) = 1/32 ≈ 0.03125
So, the probability of obtaining five heads is approximately 0.03125 or 3.125%.
(b) Probability of getting four heads:
There are five possible positions for the four heads.
P(Four Heads) = (5C4) * P(Head) * P(Head) * P(Head) * P(Head) * P(Tails) = 5 * \((1/2)^4\) * (1/2) = 5/32 ≈ 0.15625
So, the probability of obtaining four heads is approximately 0.15625 or 15.625%.
(c) Probability of getting one head:
There are five possible positions for the one head.
P(One Head) = (5C1) * P(Head) * P(Tails) * P(Tails) * P(Tails) * P(Tails) = 5 * (1/2) * \((1/2)^4\) = 5/32 ≈ 0.15625
So, the probability of obtaining one head is approximately 0.15625 or 15.625%.
For a fair die being thrown eight times:
(a) Probability of a 6 occurring six times:
The probability of rolling a 6 on a fair die is 1/6.
Since each roll is independent, we multiply the probabilities together.
P(6) = 1/6
P(Not 6) = 1 - P(6) = 5/6
P(Six 6s) = P(6) * P(6) * P(6) * P(6) * P(6) * P(6) * P(Not 6) * P(Not 6) = \((1/6)^6 * (5/6)^2\) ≈ 0.000021433
So, the probability of rolling a 6 six times is approximately 0.000021433 or 0.0021433%.
(b) Probability of a 6 never happening:
P(No 6) = P(Not 6) * P(Not 6) * P(Not 6) * P(Not 6) * P(Not 6) * P(Not 6) * P(Not 6) * P(Not 6) = \((5/6)^8\) ≈ 0.23256
So, the probability of not rolling a 6 at all is approximately 0.23256 or 23.256%.
(c) Probability of an odd number of 6s:
To have an odd number of 6s, we can either have 1, 3, 5, or 7 6s.
P(Odd 6s) = P(One 6) + P(Three 6s) + P(Five 6s) + P(Seven 6s)
\(P(One 6) = (8C1) * P(6) * P(Not 6)^7 = 8 * (1/6) * (5/6)^7P(Three 6s) = (8C3) * P(6)^3 * P(Not 6)^5 = 56 * (1/6)^3 * (5/6)^5P(Five 6s) = (8C5) * P(6)^5 * P(Not 6)^3 = 56 * (1/6)^5 * (5/6)^3P(Seven 6s) = (8C7) * P(6)^7 * P(Not 6) = 8 * (1/6)^7 * (5/6)\)
P(Odd 6s) = P(One 6) + P(Three 6s) + P(Five 6s) + P(Seven 6s)
Calculate each term and sum them up to find the final probability.
After performing the calculations, we find that P(Odd 6s) is approximately 0.28806 or 28.806%.
Learn more about binomial probability here:
https://brainly.com/question/12474772
#SPJ11
does the confidence interval provide convincing evidence that the true mean volume is different than 12 ounces? explain your answer.
Answers
The convincing evidence provided by the confidence interval depends on whether the interval includes or excludes the value of 12 ounces. If it excludes 12 ounces, it provides convincing evidence of a difference. If it includes 12 ounces, it does not provide convincing evidence of a difference.
To determine whether the confidence interval provides convincing evidence that the true mean volume is different than 12 ounces, we need to examine the confidence interval and its relationship to the value of 12 ounces.
A confidence interval is constructed based on sample data and provides a range of values within which the true population parameter is estimated to lie. The width of the confidence interval is influenced by factors such as the sample size, variability of the data, and chosen level of confidence.
If the confidence interval for the mean volume does not include the value of 12 ounces, it suggests that the true mean volume is likely to be different from 12 ounces. In this case, the confidence interval provides convincing evidence that the true mean volume is different from 12 ounces.
However, if the confidence interval does include the value of 12 ounces, it does not provide convincing evidence that the true mean volume is different from 12 ounces. This suggests that the data is consistent with the possibility that the true mean volume could be 12 ounces.
To learn more about confidence interval: https://brainly.com/question/20309162
#SPJ11
Given g(x)=2x+3, solve for x when g(x)=3
Answers
Answer:
-3/2
Step-by-step explanation:
Malachy, Sushil and Fiona share some sweets in the ratio 4:3:3. Malachy gets 8 more sweets than Fiona. How many sweets are there altogether?
Answers
Answer:
80 sweets
Step-by-step explanation:
In ratio units, Malachy gets 4-3 = 1 more than Fiona. The total number of ratio units is 4+3+3 = 10, which is 10 times that difference. This means the total number of sweets must be 10 times the difference of 8 sweets between what Malachy got and what Fiona got.
There are 8×10 = 80 sweets altogether.
__
Additional comment
Since each ratio unit stands for 8 sweets, we know the distribution is ...
Malachy: 32Sushil: 24Fiona: 24for a total of 32+24+24 = 80.
does tan^2x = sin^2x/cos^2x
Answers
Answer:
Yes they both are equal