it takes james 2.5 minutes to type 150 words at that rate how mant words can james type in 6 minutes
300
360
420
450
Answers
\(\large\huge\green{\sf{Answer:-}}\)
option b is correct\(\large\huge\green{\sf{solution:-}}\)
in 2.5 minutes word that are typed=150 in 1 minutes word that should be type= 150/2.5=60in 6minutes word that should be type= 60x6=360The number of words james can type in 6 minutes at the same rate is 360 words
Given:
Number of minutes to type 150 words = 2.5 minutes
let
number of words James can type in 6 minutes = x
Equate the ratio of the number of words to number of minutes
150 : 2.5 = x : 6
150/2.5 = x/6
cross product
150 × 6 = 2.5 × x
900 = 2.5x
x = 900/2.5
x = 360 words
Therefore, the number of words james can type in 6 minutes is 360 words
Learn more about ratio:
https://brainly.com/question/16981404
Related Questions
If you draw a card with a value of two or less from a standard deck of cards, I will pay you $463. If not, you pay me $36. (Aces are considered the
highest card in the deck. )
Find the expected value of the proposition. Round your answer to two decimal place
Answers
The expected value of the proposition round to two decimal places will be $2.38.
In parameter estimation, the expected value is an application of the weighted sum. Informally, the expected value is the simple average of a considerable number of individually determined outcomes of a randomly picked variable.
The expected value is given below.
E(x) = np
Where n is the number of samples and p is the probability.
The number of winning events when a value of two or less is 4. Thus, the probability is calculated as,
\(p = \dfrac{4}{52}\\\\p = \dfrac{1}{13}\\\\q = 1 - p\\\\ q = 1 - \dfrac{1}{13}\\\\q = \dfrac{12}{13}\)
The expected value of the proposition is calculated as,
\(E = \$463 \times \dfrac{1}{13} - \$36 \times \dfrac{12}{13}\\\\E = \$35.615 - 33.231\\\\E \approx \$2.384\)
The expected value of the proposition is $2.38.
More about the expected value link is given below.
https://brainly.com/question/13945225
#SPJ12
2. there are many ways you can accomplish a 1000-fold dilution. propose 3 different serial dilution methods that will accomplish a dilution with a 1:1000 dilution factor.
Answers
The three different dilution methods that will accomplish a dilution with a 1:1000 dilution factor are one-step dilution, two-step dilution and three-step dilution.
1. One-step dilution: Take 1 mL of the original solution and add 999 mL of the diluent (water, buffer, etc.) to get a 1:1000 dilution.
2. Two-step dilution: Take 1 mL of the original solution and add it to 9 mL of the diluent to get a 1:10 dilution. Then, take 1 mL of the 1:10 dilution and add 9 mL of the diluent to get a 1:100 dilution. Repeat this step once more to get a 1:1000 dilution.
3. Three-step dilution: Take 1 mL of the original solution and add it to 4 mL of the diluent to get a 1:5 dilution. Then, take 1 mL of the 1:5 dilution and add it to 4 mL of the diluent to get a 1:25 dilution. Repeat this step twice more to get a 1:125 dilution and then a 1:625 dilution. Finally, take 1 mL of the 1:625 dilution and add it to 375 mL of the diluent to get a 1:1000 dilution.
To learn more about dilution factor:
https://brainly.com/question/30893079#
#SPJ11
What is the value of t in this equation?
(-12)-5 =jt

Answers
Answer:
t = 60
Step-by-step explanation:
Using the rule of exponents
\((a^m)^{n}\) = \(a^{mn}\) , then
\((j^{-12}) ^{-5}\)
= \(j^{(-12(-5))}\)
= \(j^{60}\)
Then t = 60
Mahek owns a holiday tree farm. There are currently 800 trees on the property. Each year 20% of the trees are harvested and sold, and 200 seedlings are planted. Write a recursive definition for the number of trees on the farm at the beginning of the nth year.
1. a1 = 800, an = 0.20an-1 +200
2. a1 = 200, an = 0.80an-1 + 800
3. a1 = 800, an = 0.80an-1 + 200
4. a1= 0.20, an=0200an-1
Answers
The equation of the sequence will be \(\rm a_n = 0.8 \times a_{n -1} +200\),
where a₁ = 800. Then the correct option is C.
What is the geometric sequences?Let a₁ be the first term and r be the common ratio. Then the geometric sequences will be
\(\rm a_n = a_{n -1} \cdot r\)
Mahek owns a holiday tree farm.
There are currently 800 trees on the property.
Each year, 20% of the trees are harvested and sold, and 200 seedlings are planted.
Then the equation of the sequence will be
\(\rm a_n = 0.8 \times a_{n -1} +200\)
Where a₁ = 800.
Then the correct option is C.
More about the geometric sequences link is given below.
https://brainly.com/question/11266123
#SPJ1
Answer:
3. a1 = 800, an = 0.80an-1 + 200
Step-by-step explanation:
i need help understanding solving linear systems by substitution:3x + 6y = -182y = 3x - 22
Answers
The basic concept of solving a system of equations using substitution is:
- solve for one of the variables in one of the equations
- substitute this into the other equation and solve for the remaining variable
- substitute the variable you found into either equations to find the other variable.
The system of equations is:
\(\begin{gathered} 3x+6y=-18 \\ 2y=3x-22 \end{gathered}\)We can see that in the second equation "y" is almost solved, we just need to pass the "2" to the other side, so let's use this equations a solve for "y":
\(\begin{gathered} 2y=3x-22 \\ y=\frac{3x-22}{2} \end{gathered}\)Now, we can substitute "y" into the other equations, that is, the first one:
\(\begin{gathered} 3x+6y=-18 \\ 3x+6\frac{(3x-22)}{2}=-18 \end{gathered}\)Now, the equations has only "x", so we can solve for it:
\(\begin{gathered} 3x+3(3x-22)=-18 \\ 3x+9x-66=-18 \\ 12x=-18+66 \\ 12x=48 \\ x=\frac{48}{12} \\ x=4 \end{gathered}\)And now that we know that x = 4, we can substitute this into any of the two equations. Let's do it in the second:
\(\begin{gathered} 2y=3x-22 \\ 2y=3\cdot4-22 \\ 2y=12-22 \\ 2y=-10 \\ y=-\frac{10}{2} \\ y=-5 \end{gathered}\)So, the solution of the given system of equations is x = 4 and y = -5.
The illustration shows a wheelchair ramp from the side. The support at BC binds the ramp to the floor. Are Triangles ABC and ADE similar?

Answers
Triangle ABC is similar to triangle ADE by AA test of similarity
What is similarity in triangle?Similarity is a property which says that the respective angles of two triangles are of equal measure and corresponding sides are in proportion.
here, we have,
There are different types of similarity test by which we can prove the similarity of triangles.
We are given that BC is parallel to Line DE
As the lines are parallel the respective angle are corresponding angles
hence Angle D = Angle B
And Angle E = Angle C
And both triangle have angle A as common angle
By AA test of similarity we can say that the two triangles are similar
Hence by AA test similarity the two triangles are similar
To learn more about similar triangle please refer
brainly.com/question/14285697
#SPJ1
Find a particular solution of the given non-homogenous equation by the method of variation of parameter. x2y'' + xy' + (x2 - 0.25)y = 3x3/2sinx, x> 0 Given y1(x)=x-1/2sinx and y2(x) = x-1/2cosx
Answers
The particular solution to the non-homogeneous equation is:
y_p(x) = [(3/2)*ln(x)*cos(x) + (3/2)sin(x)/x + C1](x^(1/2)*sin(x) - (1/2)*x^(1/2)*cos(x)) - [(3/2)*ln(x)*sin(x) - (3/2)cos(x)/x + C2](x^(1/2)*cos(x) + (1/2)*x^(1/2)*sin(x))
To use the method of variation of parameters, we first need to find the general solution to the homogeneous equation:
x^2y'' + xy' + (x^2 - 0.25)y = 0
We assume a solution of the form y = e^(r*x), then substitute this into the equation and get the characteristic equation:
r^2 + r - 1/4 = 0
Solving for r gives us r = (-1 ± sqrt(5))/2. Thus, the general solution to the homogeneous equation is:
y_h(x) = c1*x^(1/2)sin(x) + c2x^(1/2)*cos(x)
To find a particular solution to the non-homogeneous equation, we assume a solution of the form:
y_p(x) = u(x)*y1(x) + v(x)*y2(x)
where y1(x) and y2(x) are the two linearly independent solutions to the homogeneous equation, and u(x) and v(x) are functions to be determined.
We can calculate the first and second derivatives of y_p(x) as:
y_p'(x) = u'(x)*y1(x) + v'(x)*y2(x) + u(x)*y1'(x) + v(x)*y2'(x)
y_p''(x) = u''(x)*y1(x) + v''(x)y2(x) + 2u'(x)y1'(x) + 2v'(x)*y2'(x) + u(x)*y1''(x) + v(x)*y2''(x)
Substituting y_p(x), y_p'(x), and y_p''(x) into the non-homogeneous equation and simplifying, we get:
u'(x)*x^(3/2)*sin(x) + v'(x)*x^(3/2)*cos(x) = 3x^(3/2)*sin(x)
Solving for u'(x) and v'(x), we get:
u'(x) = 3cos(x)/(2x) and v'(x) = -3sin(x)/(2x)
Integrating both sides, we get:
u(x) = (3/2)*ln(x)*cos(x) + (3/2)*sin(x)/x + C1
v(x) = (-3/2)*ln(x)*sin(x) + (3/2)*cos(x)/x + C2
where C1 and C2 are constants of integration.
Therefore, the particular solution to equation is:
y_p(x) = [(3/2)*ln(x)*cos(x) + (3/2)sin(x)/x + C1](x^(1/2)*sin(x) - (1/2)*x^(1/2)*cos(x)) - [(3/2)*ln(x)*sin(x) - (3/2)cos(x)/x + C2](x^(1/2)*cos(x) + (1/2)*x^(1/2)*sin(x))
where C1 and C2 are constants of integration.
To know more about non-homogeneous equation:
https://brainly.com/question/16921211
#SPJ4
help please!! this is for tonight, I don't know how to use the "undefined" please help

Answers
The equation of the line in slope-intercept form, with the point (4, -5) and an undefined rate of change is x = 4.
What is the slope-intercept form?Mathematically, the slope-intercept form of a line can be calculated by using this equation:
y = mx + c
Where:
m represents the slope or rate of change.x and y represents the data points.c represents the y-intercept.In Mathematics, any line that has an undefined slope (rate of change) is a vertical line because it does not have a y-intercept. This ultimately implies that, a vertical line that is parallel to the y-coordinate (y-axis) would have an undefined slope (rate of change).
Generally speaking, the equation of a line that has an undefined slope (rate of change) is given by this mathematical expression;
x = a
Where:
a represents the x-intercept.
At point (4, -5), the required equation with an undefined slope (rate of change) is x = 4.
Read more on slope here: brainly.com/question/3493733
#SPJ1
#3, #19, and #16 please!!



Answers
To answer number 19, do 21-11= 10 This means that X=10
X(10) plus 11=21
21=21
[10 + 11] >_ 21
To solve 16.
Add 3 to 13 to get 16
Then you’ll have [3x +4] >_ 16
Once you have this, subtract 4 from both sides.
Then you’ll have 3x>_ 12
Now you can divide each side by 3 to get x>_4. X=4
So if we plug that in [3x +4] >_ 13, you’ll get
[3(4) +4] >_ 13
And then you’ll get
[16] >_ 13
I hope this helps!!
cash+of+$12,000+will+be+received+in+year+6.+assuming+an+opportunity+cost+of+capital+of+7.2%,+which+of+the+following+is+true?
Answers
The true statement about the receipt of a cash of $12,000 in year 6 at an opportunity cost of capital of 7.2% is C. The present value is $7,907.
How the present value is determined:The present value of the future cash value of $12,000 can be determined by discounting.
The discount factor can be computed as (1 - 0.072)⁶.
The present value can also be computed using an online finance calculator as follows:
N (# of periods) = 6 years
I/Y (Interest per year) = 7.2%
PMT (Periodic Payment) = $0
FV (Future Value) = $12,000
Results:
Present Value (PV) = $7,907.01
Total Interest = $4,092.9
Thus, the present value of $12,000 at 7.2% discount rate is Option C.
Learn more about the present value athttps://brainly.com/question/20813161.
#SPJ1
Question Completion:A. The future value is $18,212
B. The present value is $7,996
C. The present value is $7,907
D. Provide data for tax purposes
A store sells 5 T-shirts for $48.60. What is the unit cost per T-shirt? A. $9.72 B. $8.10 C. $43.60 D. $0.10
Answers
Answer:$9.72
Step-by-step explanation: 48.60 DIVIDED BY 5 EQUALS 9.72
GIVE ME BRAINLEST PLSS
Suppose that we want to prove that 1/2 · 3/4 ··· 2n-1/2n < 1/√3n for all positive integers n. a) Show that if we try to prove this inequality using mathematical induction, the basis step works, but the inductive step fails. b) Show that mathematical induction can be used to prove the stronger inequality 1/2 · 3/4 ··· 2n-1/2n < 1/√3n+1 for all integers greater than 1, which, together with a verification for the case where n = 1, establishes the weaker inequality we originally tried to prove using mathematical induction.
Answers
The weaker inequality 1/2 · 3/4 ··· 2n-1/2n < 1/√(3n) holds for all positive integers n, but using mathematical induction, the basis step works, although the inductive step fails.
a) If we try to prove the inequality 1/2 · 3/4 ··· 2n-1/2n < 1/√(3n) using mathematical induction, we can see that the basis step works. When n = 1, we have 1/2 < 1/√3, which is true.
Now, let's consider the inductive step. Assuming that the inequality holds for some positive integer k, we need to show that it also holds for k+1, i.e., we assume 1/2 · 3/4 ··· 2k-1/2k < 1/√(3k) and we want to prove 1/2 · 3/4 ··· 2k-1/2k · (2k+1)/(2k+2) < 1/√(3k+3).
If we attempt to manipulate the expression, we can simplify it to (2k+1)/(2k+2) < 1/√(3k+3). However, we cannot proceed further to prove this inequality, as it is not necessarily true. Therefore, the inductive step fails, and we cannot establish the original inequality using mathematical induction.
b) However, mathematical induction can still be used to prove the stronger inequality 1/2 · 3/4 ··· 2n-1/2n < 1/√(3n+1) for all integers greater than 1. We can start by verifying the case where n = 1, which gives us 1/2 < 1/√4, which is true.
Now, assuming the inequality holds for some integer k, we can multiply both sides of the inequality by (2k+3)/(2k+2) to get:
(1/2 · 3/4 ··· 2k-1/2k) · (2k+3)/(2k+2) < 1/√(3k+1) · (2k+3)/(2k+2).
Simplifying the expression on both sides, we have:
(2k+3)/(2k+2) < 1/√(3k+1) · (2k+3)/(2k+2).
We can observe that the right side of the inequality is less than 1/√(3k+3) by multiplying the denominator of the right side by (2k+3)/(2k+3). Hence, we obtain:
(2k+3)/(2k+2) < 1/√(3k+3).
This establishes the inequality for k+1, and thus, we have proven the stronger inequality using mathematical induction.
By verifying the case where n = 1 separately, we can conclude that the weaker inequality 1/2 · 3/4 ··· 2n-1/2n < 1/√(3n) holds for all positive integers n, as it follows from the proven stronger inequality using mathematical induction.
Learn more about mathematical induction here:
https://brainly.com/question/29503103
#SPJ11
Given the related graph for each equation, determine the graph that represents a quadratic equation that has one real solution.
Answers
Answer:
The answer would be D. 0=2(x-1)squared
Step-by-step explanation:
Answer:
d
Step-by-step explanation:
Let |q| = 5 at an angle of 45° and |r| = 16 at an angle of 300°. what is |q – r|? 13.0 14.2 15.5 18.0
Answers
If |q| = 5 at an angle of 45° and |r| = 16 at an angle of 300°. then the
|q – r| will be 18.0
To find |q - r|, we need to subtract the complex numbers q and r after which discover the magnitude (or absolute value) of the end result.
First, we want to express q and r in rectangular form, which means that finding their actual and imaginary additives:
For q, we've:
|q| = 5 at an perspective of 45°
Re(q) = |q| cos(45°) = five cos(45°) = 5/√2
Im(q) = |q| sin(45°) = 5 sin(45°) = 5/√2
So q = (5/√2) + (5/√2)i
For r, we have:
|r| = 16 at an angle of 300°
Re(r) = |r| cos(300°) = 16 cos(300°) = sixteen(-√3/2) = -8√three
Im(r) = |r| sin(300°) = 16 sin(300°) = -8
So r = -8√three - 8i
Now we are able to discover q - r by using subtracting the actual and imaginary additives:
q - r = (5/√2) + (5/√2)i - (-8√3 - 8i)
= (5/√2) + 8√3 + (5/√2 + 8)i
To discover |q - r|, we want to take the importance of this complex number:
|q - r| = √[(5/√2 + 8√3)² + (5/√2 + 8)²]
= √[25/2 + 80√3 + 192 + 50/2 + 40 + 64]
= √[125/2 + 80√3 + 256]
= √[625/4 + 320√3 + 1024]
= √[(25/2 + 16√3)²]
= 25/2 + 16√3
≈ 18.0
Hence, |q - r| is about equal to 18.0.
Learn more about Complex Number:-
https://brainly.com/question/5564133
#SPJ4
HELPPPPPPPPPPPP!!!!!!!!1

Answers
Answer:
I looked at it thoroughly and I believe your correct, I believe I have done something like this before. please tell me if I am wrong. If I am, REPORT ME so you can get your point back.
Step-by-step explanation:
Hope I helped! :D
let x denote the number of canon slr cameras sold during a particular week by a certain store. the pmf of x is x 0 1 2 3 4 px(x) 0.1 0.2 0.3 0.25 0.15
Answers
P(X = 4, Y = 2) = 0.055131
P(X = Y) = 0.35607
From the information given:
X represent no of Canon SLR
The PMF is given as:
X : 0 1 2 3 4
p(x) : 0.1 0.2 0.3 0.25 0.15
p = P(customers that purchase the camera & also purchase an extended warranty.
As a result, the conditional distribution Y provided X approaches a Binomial distribution with n = x and p = 0.55 as the parameter.
\(\frac{Y}{X}\) ~ Bin ( n= x , p =0.55) y
= 0.1 ........ x and X = 0,1,2,3,4.
The condition probabilities Y given X is:
\(P (\frac{Y = 0}{X = 0} ) =1\)
\(P (\frac{Y = 0}{X = 1} ) = 0.45 and P (\frac{Y = 1}{X = 1} ) =0.55\)
\(P (\frac{Y = 0}{X = 2} ) = 0.2025 and P (\frac{Y = 1}{X = 2} ) =0.495, P (\frac{Y = 2}{X = 2} ) =0.3025\)
\(P (\frac{Y = 0}{X = 3} ) = 0.091125 and P (\frac{Y = 1}{X = 3} ) =0.334125, \\P (\frac{Y = 2}{X = 3} ) =0.408375 and P (\frac{Y = 3}{X = 3} ) = 0.166375\)
\(P (\frac{Y = 0}{X = 4} ) = 0.0.041006 and P (\frac{Y = 1}{X = 4} ) =0.0.200475, P (\frac{Y = 2}{X = 3} ) =0.367538\)
\(P (\frac{Y = 3}{X = 4} ) = 0.299475 and P (\frac{Y = 4}{X = 4} ) =0.091506\)
Now, the joint P.D (probability Dist.) of X & Y is expressed as:
\(P (\frac{Y = y}{X = x} ) = P (\frac{Y = y. X = x}{X = x} )\)
\(P( X = x , Y = y) = P(\frac{Y = y}{X =x} ) * P(X =x)\)
The Joint P.D is;
Y Total
0 1 2 3 4
X 0 0.1 0 0 0 0 0.1
1 0.09 0.11 0 0 0 0.2
2 0.06075 0.1485 0.09075 0 0 0.3
3 0.022781 0.083531 0.102094 0.041594 0 0.25
4 0.006151 0.030071 0.055131 0.044921 0.013726 0.15
Total 0.279682 0.372103 0.247974 0.086515 0.013726 1
(a)
P(X=4,Y=2)
From the table above:
P(X=4,Y=2)
= 0.055131
(b)
P(X= Y)
= (P = 0 , Y = 0) + P( X =1, Y =1) + P( X=2, Y=2) + P(X=3,Y=3) + P(X=4,Y=4)
= 0.1 + 0.11 + 0.09075 + 0.041594 + 0.013726
= 0.35607
Learn more about Probability mass Function:
https://brainly.com/question/18688445
#SPJ4
I need something from u:
Please help me this test is due at 2:45 pm.
Please show work on how you solve it.
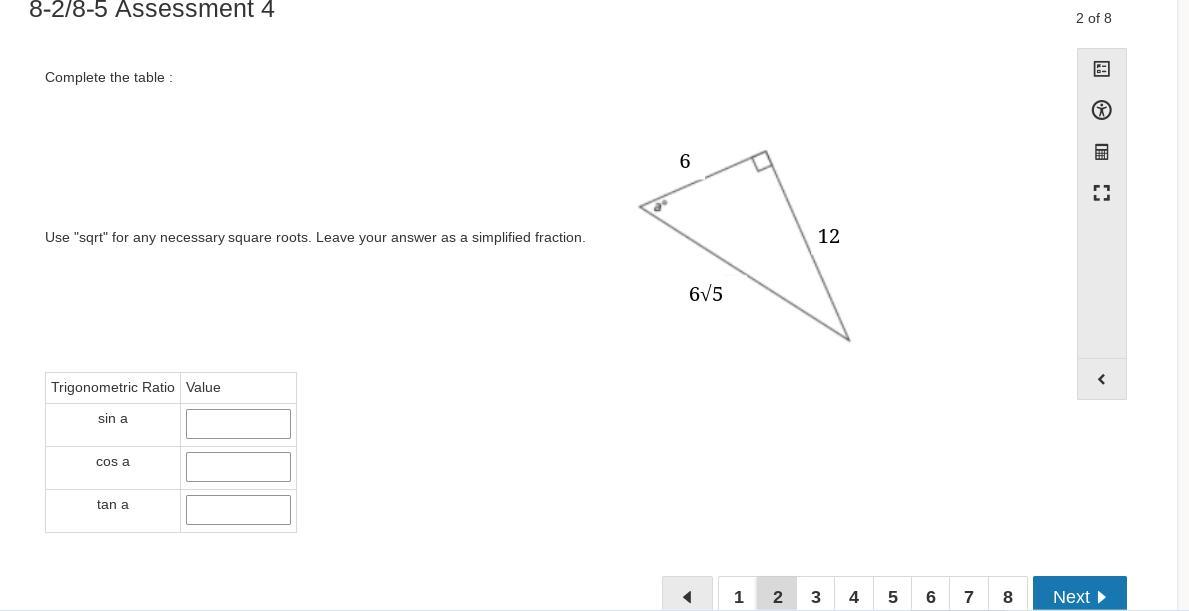
Answers
Using trigonometric ratios, the value of sin a, cos a, and tan a are 12/6√5,√5/5 and 2 respectively.
What is trigonometric ratioTrigonometric ratios are defined as the values of all the trigonometric functions based on the value of the ratio of sides in a right-angled triangle. The ratios of sides of a right-angled triangle with respect to any of its acute angles are known as the trigonometric ratios of that particular angle.
To find the value of sin a:
sin a = opposite / hypothenuse
sin a = 12 / 6√5
a = sin⁻¹(12/6√5)
a = 63.43
sin a = 12/ 6√5
b. cos a = adjacent / hypothenuse
cos a = 6 / 6√5
cos a = √5/5
c. tan a = opposite / adjacent
tan a = 12 / 6
tan a = 2
Learn more on trigonometric ratio here;
https://brainly.com/question/17155803
#SPJ1
How Solve the following questions (write all steps). Q1: Use the following data to find a recursive Nevill's method When interpdating table using Polynomial at x-4.1 f(x) X 36 1.16164956 3.8 080201036 4.0 0.30663842 4.2 035916618 -123926000. 4.4 Q2: Construct an approximation polynomial for the following data using Hermite method. 1 f(x) f'(x) x 1.2 2.572152 7.615964 1.3 3.60 2102 13-97514 1.4 5.797884 34.61546 1.5 14.101442 199.500 - Good Luck -
Answers
To find a recursive Nevill's method when interpolating a table using a polynomial at x = 4.1, we can use the following steps:
Step 1: Set up the given data in a table with two columns, one for f(x) and the other for x.
f(x) x
36 1.16164956
3.80201036 4.0
0.30663842 4.2
0.35916618 -123926000.4
Step 2: Begin by finding the first-order differences in the f(x) column. Subtract each successive value from the previous value.
Δf(x) x
-32.19798964 1.16164956
-3.49537194 4.0
-0.05247276 4.2
Step 3: Repeat the process of finding differences until we reach a single value in the Δf(x) column. Continue subtracting each successive value from the previous one.
Δ^2f(x) x
29.7026177 1.16164956
3.44289918 4.0
Step 4: Repeat Step 3 until we obtain a single value.
Δ^3f(x) x
-26.25971852 1.16164956
Step 5: Calculate the divided differences using the values obtained in the previous steps.
Divided Differences:
Df(x) x
36 1.16164956
-32.19798964 4.0
29.7026177 4.2
-26.25971852 -123926000.4
Step 6: Apply the recursive Nevill's method to find the interpolated value at x = 4.1 using the divided differences.
f(4.1) = 36 + (-32.19798964)(4.1 - 1.16164956) + (29.7026177)(4.1 - 1.16164956)(4.1 - 4.0) + (-26.25971852)(4.1 - 1.16164956)(4.1 - 4.0)(4.1 - 4.2)
Solving the above expression will give the interpolated value at x = 4.1.
Q2: To construct an approximation polynomial using the Hermite method, we follow these steps:
Step 1: Set up the given data in a table with three columns: f(x), f'(x), and x.
f(x) f'(x) x
2.572152 7.615964 1.2
3.602102 13.97514 1.3
5.797884 34.61546 1.4
14.101442 199.500 1.5
Step 2: Calculate the divided differences for the f(x) and f'(x) columns separately.
Divided Differences for f(x):
Df(x) \(D^2\)f(x) \(D^3\)f(x)
2.572152 0.51595 0.25838
Divided Differences for f'(x):
Df'(x) \(D^2\)f'(x)
7.615964 2.852176
Step 3: Apply the Hermite interpolation formula to construct the approximation polynomial.
Learn more about polynomial here:
https://brainly.com/question/11536910
#SPJ11
A graph is a straight line through the point (0, 5). Can the graph represent a proportional relationship? Explain.
A.
Yes; the constant of proportionality is 5.
B.
Yes; the equation of the line can be written in the form y = kx, where k = 5.
C.
Yes; the graph is a straight line that crosses the y-axis at (0, 5).
D.
No; the graph of a proportional relationship must pass through (0, 0).
Answers
Answer:
D No; the graph of a proportional relationship must pass through (0, 0).
Step-by-step explanation:
Determine the relationship
A. Parallel because the slopes are the same
B. Perpendicular because the slopes are opposite reciprocals
C. Oblique because the slopes are different

Answers
Answer:
Perpendicular because the slopes are opposite reciprocals
Step-by-step explanation:
__________ typically are used to display continuous measures.
Answers
Histograms typically are used to display continuous measures.
The histograms typically are used to display continuous measures.
Charts TypesThere are different types of charts: histogram, line chart, pie chart, and others.
The histogram is a type of chart used as a tool that provides a way to assess the distribution of data. From this type of chart, a set of data are previously tabulated and divided into classes. In the other words, the histogram is applied to summarize discrete or continuous measures, so it becomes more easily the understand the used data. There are many websites and software that allow the plot of this type of chart.
From the explanation, it is possible to identify the histograms typically are used to display continuous measures.
Read more about the histogram here:
https://brainly.com/question/13652813
#SPJ12
what is 12 divided by 175
need help asap or i'll fial
Answers
Answer:
Exact Form:
12
175
Decimal Form:
0.06857142
Step-by-step explanation:
find is a simple interest for a loan where birr 6,000 borrowed and the amount owned after 5 months this is for 7,500 what is the rate
Answers
Interest = Principal * Rate * Time
In this case, the principal (P) is 6,000 birr, the time (T) is 5 months, and the amount owed (A) is 7,500 birr. We need to find the rate (R).
Interest = Amount Owed - Principal
Let's substitute the values into the formula:
Interest = 7,500 - 6,000
Interest = 1,500 birr
Now we can rearrange the formula to solve for the rate:
Rate = Interest / (Principal * Time)
Rate = 1,500 / (6,000 * 5/12)
Rate = 1,500 / (30,000/12)
Rate = 1,500 * 12 / 30,000
Rate = 0.6 or 0.6 * 100 = 60%
Therefore, the rate of interest for the loan is 60%.
determine whether the raltion r on the set ofall integers is reflexin x =y^2
Answers
The relation "r" on the set of all integers, where x = y^2, is not reflexive.
A relation is reflexive if every element in the set is related to itself. In this case, for the relation x = y^2 to be reflexive, every integer "x" should be related to itself, meaning that x = x^2. However, this is not true for all integers.
For example, if we consider x = 2, it is not equal to 2^2 = 4. Similarly, if we consider x = -3, it is not equal to (-3)^2 = 9.
Since there are integers that do not satisfy the condition x = x^2, the relation x = y^2 is not reflexive on the set of all integers.
To learn more about raltion click here: brainly.com/question/30569368 #SPJ11
Plot 213, −56, and −312 on the number line.

Answers
Answer:
Step-by-step explanation:

Plot 213, −56, and −312 on the number line.
The rabbit population on Park Point in Duluth, MN at time t is modeled by the r(t) = 225 cos pi/3 t + 425 where t is measured in years. ( Park Point, by the way, is reported as the world’s longest freshwater sand spit) What is the maximum number of rabbits on Park Point during a population cycle?
1. What is the maximum number of rabbits on Park Point during a population cycle?
2. How long is the population cycle?
3. Find the approximate number of rabbits on the island after 3.2 years
Answers
Using the senoidal function, it is found that:
1. The maximum number of rabbits on Park Point during a population cycle is of 650.2. The population cycle is of 3 years.3. The approximate number of rabbits on the island after 3.2 years is 205.Senoildal function:
The function that models the population after t years is given by:
\(r(t) = 225\cos{\left(\frac{\pi}{3}\right)t} + 425\)
Item 1:
The cosine function varies between -1 and 1, hence, considering it equals to 1:
\(r_{MAX} = 225 + 425 = 650\)
The maximum number of rabbits on Park Point during a population cycle is of 650.
Item 2:
The period of a cosine function \(\cos{\frac{2\pi}{T}}\) is T.
In this problem, T = 3, hence:The population cycle is of 3 years.
Item 3:
\(r(3.2) = 225\cos{\left(\frac{\pi}{3}\right)3.2} + 425 = 205\)
The approximate number of rabbits on the island after 3.2 years is 205.
You can learn more about senoidal functions at https://brainly.com/question/13575593
A shop is offering a 15% reduction on the price of a computer .The original price of the computer was $670.what is its reduced price?
Answers
Answer:
$569.50
Step-by-step explanation:
15% deduction from the initial price(100%) will have us remaining with 85%
100% = 670
85% = 85% x 670
100%
= $569.50
Factor completely.
n^2 + 7 n - 44
A) (n + 4)(n - 11)
B) (n - 4)(n + 11)
C) (n - 4)(n - 11)
Answers
The Radius of a circle is 4 millimeters. What is the circle’s area ?
Answers
Answer:
Step-by-step explanation:
S = \(R^{2} *\pi\)
S = \(4^{2} * \pi\)
S = 16 * 3,14
S = 50,24
(PLEASE HURRY I NEED IT TODAY)
The triangle ABC goes through a series of transformations, resulting in the triangle A’B’C’. The three transformations are listed below. Reflection in the x- axis. Followed by a rotation of 1800 clockwise about the origin Followed by a translation 3 units down and 4 units to the right For triangle ABC, the vertex A is originally located at (-2, 3). Show the new coordinates of A after each of the three transformations above.
Answers
Answer:
1) Reflection in the x-axis
A' = (-2, -3)
2) Rotation of 180° clockwise about the origin
A'' = (2, 3)
3) Translation of 3 units down and 4 units to the right
A''' = (6, 0)
Step-by-step explanation:
The transformations are as follows;
1) Reflection in the x-axis
Here the x-coordinate is the same and the y-coordinate changes sign.
Therefore, we have;
A (-2, 3)
After reflection in the x-axis becomes A' = (-2, -3)
2) Rotation of 180° clockwise about the origin
When, a point (x, y) is rotated 180° clockwise about the origin, it becomes (-x, -y)
Therefore, we have;
A' = (-2, -3) becomes A'' = (2, 3)
3) Translation of 3 units down and 4 units to the right
Translation of 3 units down and 4 units to the right = \(T_{(4, -3)\)
Which gives
A''' = (2 + 4, 3 - 3) = (6, 0).