It cost 3 times more to feed a cat per week than than it does a rabbit per week and half as much to feed a hamster per week than it to feed a rabbit per week. If it cost $2.00 to feed a hamster per week, how much does it cost to feed a cat for 3 weeks
A. $9.00
B. $48.00
C. $36.00
D. $84.00
E. $25.00
F. $12.00
Answers
Your final answer: C, or $36.00.
Related Questions
The circle graph shows how Jane's family budgets a total of $45,000 for the year.
Insurance.
$3600
Utilities
$3150
Clothing.
$2700
Transportation
$1350
Entertainment-
$5400
Savings
$4050
Taxes
$7200
Food
$7650
Housing
$9900
Find the percentage of the total budgeted for each category listed below.
Answers
The percentage that each expense has out of the total budgeted amount of $45,000 have been computed, where insurance has 8.00%, Utilities 7.00% and so on.
What is a percentage?
In this case, percentage refers to proportion of each expense from the total budgeted expense of $45,000, which means that in order to total budgeted expense of $45,000, which means that in order to compute the percentage of total budgeted for each expense category, we divide the expense by the total budgeted expense
Insurance=$3600/$45,000=8.00%
Utilities=$3150/$45,000=7.00%
Clothing=$2700/$45000=6.00%
Transportation=$1350/$45000=3.00%
Entertainment=$5400/$45000=12.00%
Savings=$4050/$45000=9.00%
Taxes=$7200/$45000=16.00%
Food=$7650/$45000=17.00%
Housing=$9900/$45000=22.00%
Find out more about percentage on:https://brainly.com/question/16865197
#SPJ1
Maria, Aldo, and Boris sent a total of 102 text messages over their cell phones during the weekend. Aldo sent 2 times as many messages as Boris. Boris sent 10 fewer messages than Maria. How many messages did they each send?
Answers
Maria sent 28 messages. Aldo sent 46 messages. Maria, Aldo, and Boris sent a total of 102 text messages over their cell phones during the weekend.
Let's start by assigning variables to represent the unknowns in the problem. Let A be the number of messages Aldo sent, B be the number of messages Boris sent, and M be the number of messages Maria sent. We can use the information given in the problem to form a system of equations:
A + B + M = 102 (total messages sent)
A = 2B (Aldo sent twice as many as Boris)
B = M - 10 (Boris sent 10 fewer than Maria)
We can substitute the second equation into the third equation to get:
A = 2(M - 10) (substitute B with M - 10)
Now we have two equations involving only A and M:
A + (M - 10) + M = 102 (substitute B with M - 10 in first equation)
A = 2(M - 10) (substitute B with M - 10 in third equation)
We can simplify the first equation by combining like terms:
2M - 10 + A = 102
And we can simplify the second equation by distributing the 2:
A = 2M - 20
Now we have a system of two equations with two unknowns:
2M - 10 + A = 102
A = 2M - 20
We can solve for A in the second equation:
A = 2M - 20
A + 20 = 2M
M = (A + 20)/2
We can substitute this expression for M into the first equation:
2M - 10 + A = 102
2((A + 20)/2) - 10 + A = 102
A + 20 - 10 + A = 102
2A + 10 = 102
2A = 92
A = 46
So Aldo sent 46 messages. We can use the equation B = M - 10 to find Boris's number of messages:
B = M - 10
B = (A + 20)/2 - 10
B = (46 + 20)/2 - 10
B = 28
So Boris sent 28 messages. Finally, we can use the first equation to find Maria's number of messages:
A + B + M = 102
M = 102 - A - B
M = 102 - 46 - 28
M = 28
Therefore, Maria sent 28 messages.
Learn more about cell phones here
https://brainly.com/question/30487302
#SPJ11
what must be your average speed in order to travel 350 km in 5.15 h?
Answers
Answer:
68 km/h--------------
Average speed equation:
s = d/t, where d- total distance, t - total timeSubstitute 350 for d and 5.15 for t:
s = 350/5.15s = 67.96 ≈ 68 km/hThe average speed must be approximately 68 km per hour.
At the beginning of the first day of the experiment the mass of the substance was 1300 grams and mass was decreasing by 14% per day. Determine the mass of the radioactive sample at the beginning of the 11th day of the experiment.
Answers
The mass of the radioactive sample at the beginning of the 11th day of the experiment is approximately 286 grams.
How to find the mass?Since the mass is decreasing by 14% per day, we can find the mass at the beginning of each day by multiplying the previous day's mass by 0.86 (which is 100% - 14%).
At the beginning of the first day, the mass was 1300 grams.
At the beginning of the second day, the mass is:
1300 grams x 0.86 = 1118 grams (rounded to the nearest gram)
At the beginning of the third day, the mass is:
1118 grams x 0.86 = 962 grams (rounded to the nearest gram)
We can continue this pattern to find the mass at the beginning of the 11th day:
Mass at the beginning of the fourth day: 962 grams x 0.86 = 828 grams
Mass at the beginning of the fifth day: 828 grams x 0.86 = 711 grams
Mass at the beginning of the sixth day: 711 grams x 0.86 = 612 grams
Mass at the beginning of the seventh day: 612 grams x 0.86 = 526 grams
Mass at the beginning of the eighth day: 526 grams x 0.86 = 452 grams
Mass at the beginning of the ninth day: 452 grams x 0.86 = 388 grams
Mass at the beginning of the tenth day: 388 grams x 0.86 = 333 grams
Mass at the beginning of the eleventh day: 333 grams x 0.86 = 286 grams (rounded to the nearest gram)
Therefore, the mass of the radioactive sample at the beginning of the 11th day of the experiment is approximately 286 grams.
To know more about grams visit:
https://brainly.com/question/29127168
#SPJ1
HELP ASAP!!!
Find the area of the figure. Round your answer to the nearest hundredth.
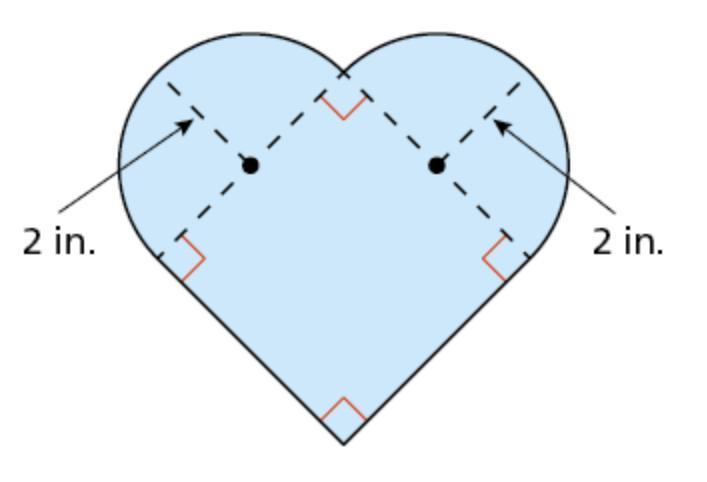
Answers
Answer:
28.57 in²
Step-by-step explanation:
the square must be 4 in by 4in so the area = 16in²
the two semicircles are made up of quarter circles with a radius of 2 inches and are equal --> together makes one full circle
area of a circle = \(\pi r^{2}\)
r = 2 r² = 4
area of circle = 12.56637061
area of circle + area of square = 28.566
28.57
1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19+20=
A)0
B)210
C)220
D)Brainliest
Answers
\(\\ \rm\longrightarrow 1+2\dots +20\)
Use Summation formula
\(\\ \rm\longrightarrow S_n=\dfrac{n(n+1)}{2}\)
\(\\ \rm\longrightarrow S_{20}=\dfrac{20(20+1)}{2}\)
\(\\ \rm\longrightarrow S_{20}=\dfrac{20(21)}{2}\)
\(\\ \rm\longrightarrow S_{20}=\dfrac{420}{2}\)
\(\\ \rm\longrightarrow S_{20}=210\)
Use the table to answer the questions No Birth Control Birth Control No BRCA Gene 20 30 BRCA Gene 50 ? Using the additive model what value would we expect in cell d? 50 O 60 30 40
Answers
The distribution of individuals based on two factors: the presence or absence of birth control (rows) and the presence or absence of the BRCA gene (columns). The numbers in each cell represent the count of individuals falling into a specific category.
In the additive model, the values in the cells are independent of each other, and the expected count in any given cell is obtained by adding the row total and column total for that cell and subtracting the grand total. The formula for the additive model is:
Expected count in cell = (Row total * Column total) / Grand total
We are given the values for cells a, b, and c. Using the provided table, we can calculate the row and column totals:
Row total for row 1 (No Birth Control) = 20 + 30 = 50
Row total for row 2 (Birth Control) = 50 + x (value in cell d)
Column total for column 1 (No BRCA Gene) = 20 + 50 = 70
Column total for column 2 (BRCA Gene) = 30 + x (value in cell d)
Grand total = 20 + 30 + 50 + x (values in all cells)
Now, let's substitute these values into the additive model formula:
(50 * (30 + x)) / (20 + 30 + 50 + x) = 50
Next, we can cross-multiply and solve for x:
50 * (30 + x) = 50 * (100 + x)
1500 + 50x = 5000 + 50x
By canceling out the 50x terms on both sides, we get:
1500 = 5000
However, this equation has no solution. It indicates that the given table is not consistent with the additive model. Consequently, we cannot determine the expected value in cell d using the additive model with the provided information.
Learn more about BRCA gene :
https://brainly.com/question/31625200
#SPJ11
Some tennis player's believe they have a better chance of winning the point if they are the one serving for the point. Suppose that in a particular match, Samson wins 46 of the 62 points when he's serving but only 23 of the 52 points when his opponent is serving. Does this data give convincing evidence that Samson plays better when serving? a) How much better did Samson perform when serving? Calculate the difference in the percentage of points won (the test statistic). Show work. b) State the hypotheses we are interested in testing. c) Suppose that the results of a simulation gave a p-value of 0.24, interpret this value. d) What conclusion would you make based on the p-value from part d? e) If your conclusion from part d was in error, what type of error did you commit? Explain. f) Describe this type of error in context. 9) Describe how to reduce the likelihood of this error occurring. h) If we concluded that Samson's ability to win points when serving is lower than his ability to win points when his opponent is serving, can we conclude that his serving is the cause of the difference?
Answers
(A) Total number of points served by Samson and multiply by 100 (B) Null hypothesis(H0) and Alternative hypothesis (Ha) (C) there would be a 24% chance of observing a difference in performance as extreme as the one observed in the data.
(D) Based on the p-value of 0.24, we do not have strong evidence to reject the null hypothesis. (E) it would be a Type II error. (F) Type II error would mean that we concluded there is no difference in Samson's performance when serving and when his opponent is serving, but in reality, there is a difference. (G) To reduce the likelihood of a Type II error occurring, we can increase the sample size (H) No, we cannot conclude that Samson's serving is the cause of the difference in his ability to win points when serving compared to when his opponent is serving
a) The difference in the percentage of points won when serving and when the opponent is serving can be calculated by subtracting the percentage of points won when the opponent is serving from the percentage of points won when serving. To find the percentage of points won when serving, we divide the number of points won when serving by the total number of points served by Samson and multiply by 100. Similarly, to find the percentage of points won when the opponent is serving, we divide the number of points won when the opponent is serving by the total number of points served by the opponent and multiply by 100.
b) The hypotheses we are interested in testing are:
- Null hypothesis (H0): There is no difference in Samson's performance when serving and when his opponent is serving.
- Alternative hypothesis (Ha): Samson performs better when serving compared to when his opponent is serving.
c) A p-value of 0.24 indicates that if the null hypothesis were true, there would be a 24% chance of observing a difference in performance as extreme as the one observed in the data. In other words, the p-value represents the probability of obtaining the observed difference in performance or a more extreme difference, assuming that there is no actual difference in Samson's performance when serving.
d) Based on the p-value of 0.24, we do not have strong evidence to reject the null hypothesis. This means that the data does not provide convincing evidence that Samson plays better when serving compared to when his opponent is serving.
e) If our conclusion from part d was in error, it would be a Type II error. This occurs when we fail to reject the null hypothesis even though it is false. In this case, it would mean that there is a difference in Samson's performance when serving, but we failed to detect it.
f) In the context of this question, a Type II error would mean that we concluded there is no difference in Samson's performance when serving and when his opponent is serving, but in reality, there is a difference. This could potentially lead to underestimating Samson's ability to perform better when serving.
g) To reduce the likelihood of a Type II error occurring, we can increase the sample size. By collecting more data, we can increase the power of our test and improve our ability to detect a difference in performance if it truly exists. Additionally, we can also adjust the significance level of our test (e.g., from 0.05 to 0.01) to make it more likely to detect smaller differences.
h) No, we cannot conclude that Samson's serving is the cause of the difference in his ability to win points when serving compared to when his opponent is serving. The data provided only shows an association between serving and winning points, but it does not establish a causal relationship. Other factors, such as skill, strategy, or the opponent's performance, could also contribute to the difference observed. To establish causality, further investigation and controlled experiments would be needed.
To know more about hypotheses refer to:
https://brainly.com/question/25263462
#SPJ11
joe is a wrestler and during his workouts he loses 2 pounds. how much water would he have to drink to replenish this water weight loss?
Answers
Answer:
36 ounces or if over 150 lbs drink more water than 36 ounces
Step-by-step explanation:
For every pound of sweat you lose you need to drink 16 ounces of water!
On 1 st March, 2020 Mr. Mohit started a Furniture business in GANDHI NAGAR Mr. Mohit invested Rs 50,00,000.
Answers
Answer:
Answer to the following question is as follows;
Step-by-step explanation:
Given:
Amount invested by Mr. Mohit = Rs. 50,00,000
Computation:
Books of (...... LTD)
Journal entries
Date Particular Debit Credit
March 1 Cash A/C Dr. 50,00,000
To Capital A/C Cr. 50,00,000
(Being Amount invested in new business)
 Write down the first three terms of the sequence described.
The first term is 7; the term-to-term rule is 'add 3
Answers
Answer:
7, 10, 13, 16
Step-by-step explanation:
Given,
Frist term=7
term-to-term rule is add 3
Therefore first three terms will be
7, 7+3=10, 10+3= 13, 13+3=16
At Weichert Realty, each agent earns 7% commission on their sales. If they sell a house for $300,000, they would earn $21,000. How much would
they have to sell in order to earn $35,000?
$50,000
B) $25,000
$2,450
$500,000
Answers
Sell $500,000 worth of real estate in order to earn a commission of $35,000 at a rate of 7%. So the correct answer is D) $500,000.
Use the given information to set up a proportion and solve for the unknown sales amount:
Commission earned / Sales amount = Commission rate
$21,000 / $300,000 = 0.07
Now we can use this proportion to find the sales amount needed to earn $35,000:
$35,000 / 0.07 = $500,000
Therefore, they would need to sell $500,000 worth of real estate in order to earn a commission of $35,000 at a rate of 7%. So the correct answer is D) $500,000.
To know more about commission follow
https://brainly.com/question/12298724
#SPJ1
What Is The Area Of The Sector Below? Explain Steps

Answers

david is asked to tell the researcher what he sees in a series of inkblots. he is completing a
Answers
David is completing a Rorschach test, which is a type of projective psychological assessment. The test consists of a series of inkblots presented to the participant, and their responses are analyzed by the researcher to gain insights into their personality, thought processes, and emotional functioning.
The Rorschach test is a widely used tool in clinical psychology and has been subject to much controversy and debate over its validity and usefulness in assessment.
Visit here to learn more about Rorschach test brainly.com/question/9357165
#SPJ11
Find a linear function h given h(-1)=-2 and h(-7)=-9 The linear function is h(x)= (Simplify your answer. Use integers or fractions for any numbers in the expression.)
Answers
h(x) = -7/6x - 25/6.
Given h(-1)=-2 and h(-7)=-9
For linear function h(x), we can use slope-intercept form which is y = mx + b, where m is the slope and b is the y-intercept.
To find m, we can use the formula: m = (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are two points on the line.
h(-1) = -2 is a point on the line, so we can write it as (-1, -2).
h(-7) = -9 is another point on the line, so we can write it as (-7, -9).
Now we can find m using these points: m = (-9 - (-2)) / (-7 - (-1)) = (-9 + 2) / (-7 + 1) = -7/6
Now we can find b using one of the points and m. Let's use (-1, -2):
y = mx + b-2 = (-7/6)(-1) + b-2 = 7/6 + b
b = -25/6
Therefore, the linear function h(x) is:h(x) = -7/6x - 25/6
We can check our answer by plugging in the two given points:
h(-1) = (-7/6)(-1) - 25/6 = -2h(-7) = (-7/6)(-7) - 25/6 = -9
The answer is h(x) = -7/6x - 25/6.
Know more about linear function here,
https://brainly.com/question/29205018
#SPJ11
Determine all values of h and f for which the system x + 3y = h and -4x + ky = -9 has no solution.
Answers
For any price of h and k = -12, the system x + 3y = h and -4x + ky = -9 will haven't any answer.
To determine the values of h and okay for which the device of equations has no answer, we want to locate the situations underneath which the equations are inconsistent or parallel.
The given system of equations is:
Equation 1: x + 3y = h
Equation 2: -4x + ky = -9
For the gadget to haven't any answer, the lines represented with the aid of these equations should be parallel and in no way intersect. In different phrases, the slopes of the traces need to be equal, but the y-intercepts should be specific.
Let's first discover the slopes of the traces. The slope-intercept form of Equation 1 is y = (-1/3)x + (h/3), wherein the slope is -1/3. The slope-intercept shape of Equation 2 is y = (4/k)x - (9/k), wherein the slope is 4/k.
For the strains to be parallel, the slopes should be equal. Therefore, we have the condition: -1/3 = 4/k.
To locate the values of h and okay for which the gadget has no answer, we need to locate the values of h that satisfy the situation -1/3 = 4/k.
Solving this equation for ok, we've got:
-1/3 = 4/k
-1 = 12/k
k = -12
Substituting k = -12 returned into the equation -1/3 = 4/k, we've:
-1/3 = 4/(-12)
-1/3 = -1/3
Since the equation holds real for any value of h, there aren't any restrictions at the price of h.
Therefore, for any price of h and k = -12, the system x + 3y = h and -4x + ky = -9 will haven't any answer.
To know more about equations,
https://brainly.com/question/29797709
#SPJ4
The system of equations has no solution when k is equal to 12. The value of h can be any real number.
To determine the values of h and f for which the system has no solution, we need to analyze the coefficients of the variables and the constants in the equations.
The given system of equations is:
x + 3y = h
-4x + ky = -9
We can rewrite the second equation as:
-4x + ky = -9
Dividing both sides of the equation by -4, we get:
x - (k/4)y = 9/4
Comparing the coefficients of x and y in the two equations, we can see that the slopes of the lines represented by the equations are different when k is not equal to 12.
Therefore, for the system to have no solution, k must be equal to 12.
As for the value of h, it can be any real number since it does not affect the slopes of the lines.
Learn more:About system of equations here:
https://brainly.com/question/21620502
#SPJ11
There are 530 estudents in my class 30% are footballers.how many students are not footballers
Answers
Answer:
371 students
Step-by-step explanation:
100% = 530
10% = 53
30% = 53 x 3 = 159
159 students are footballers.
Now we subtract.
530 - 159 = 371
371 students are not footballers.
Hope this helps!
You use a garden hose to fill a wading pool. If the water level rises 13 centimeters every 5 minutes and you record the data point of (10,y), what is the value of y? Use slope to justify your answer.
Answers
2sin60° sin90°+ cos60°cos0
Answers
Answer:
\(\sqrt{3 }\) + \(\frac{1}{2}\)
Step-by-step explanation:
Using exact values
2sin60°sin90° + cos60°cos0°
= 2 × \(\frac{\sqrt{3} }{2}\) × 1 + \(\frac{1}{2}\) × 1
= \(\sqrt{3}\) + \(\frac{1}{2}\) ← exact value
Alana sold 6 oranges for $3. Write the equation that represents the price for any number of oranges.
Answers
Answer:
50 cents ($0.50)
Step-by-step explanation:
We need to find the price for one orange. To get one orange, you have to divide 6 by 6. Anything you do to one side of the equation must be done to the other side. You have to divide 3 by 6. If you do this, you get .5, or 1/2. In money, that translates to 50 cents.
Hope this helps!
Step-by-step explanation:
the price of one orange is indeed 3/6 = 1/2 = $0.50.
the equation residential the price for any number of oranges contains then a variable, say x, to stand for the number of purchased oranges :
p(x) = 0.5x
meaning that the price of x oranges is 0.5×x.
Find a parametrization of the line in which the planes x + y + z = 9 and y + z = 3 intersect. Find the parametrization of the line. Let z = t. X=. Y=0,2=0 -Oz-| -00
Answers
This parametrization allows you to express any point on the line by choosing a value for the parameter t.
From the equation y + z = 3, we can express y in terms of z as y = 3 - z.
Substituting this expression for y into the equation x + y + z = 9, we have x + (3 - z) + z = 9.
Simplifying, we get x + 3 = 9.
Rearranging the equation, we have x = 6.
Now we have the following parametrization:
x = 6
y = 3 - z
z = t
where t is a parameter representing the value of z.
Thus, the parametrization of the line formed by the intersection of the planes x + y + z = 9 and y + z = 3 is:
x = 6,
y = 3 - t,
z = t.
This parametrization allows you to express any point on the line by choosing a value for the parameter t.
Learn more about parametrization
https://brainly.com/question/28537985
#SPJ11
PLZ I NEED IT
Andy buys a new car for $23,540. He estimates that the car will decrease in value by about 5% each year. Which of the following functions best models this situation?
Answers
Answer: y=0.05x-23540
Step-by-step explanation: We turn 5% into a decimal which is 0.05 and we add x to it so we can pick how many years. Then we subtract 23540 because he has used that money to buy the car.
in 3x + 2/3y - 15 < 0, the point (x,9) is a solution for the inequality shown. what is the possible value for x?
a: 2
b: 3
c: 4
d: 5
Answers
answer: 2
explanation:
if you plug in all of the numbers available for the equation and using 9 as a substitute for y, you'll see that it will either = 0 or be greater than 0
heres another one.
for brainliest

Answers
Answer:
Max made a mistake in step 5.
He should have used division instead of multiplication.
Step-by-step explanation:
In step #5, he made the mistake of multiply 5/6 by 5/6. The reason why this doesn't work is because y is not a full y. When there isn't a number beside a variable, it is implied that it is 1y. To solve for y, you need 1y or else results or inaccurate.
In reality, 5/6 * 5/6 is equal to 25/36. If you divided 5/6 by 5/6, it is equal to 1, which makes y a full y.
Answer:
he made a lot of mistakes, but i'd say he used division instead of multiplication in step 5
(but the biggest mistake was adding 1/6 to both sides instead of multiplying by it)
Step-by-step explanation:
4. Construct a circle with center V. Construct an equilateral triangle RST inscribed within the circle.
Answers
A circle with center V and an inscribed equilateral triangle RST.
What is circle?
A circle is a closed two-dimensional shape consisting of all the points that are equidistant from a given point, called the center.
To construct a circle with center V and an inscribed equilateral triangle RST, follow these steps:
Draw point V as the center of the circle.
From point V, draw a radius that will serve as one side of the equilateral triangle RST. Label the endpoint of this radius as point S.
Using a compass, draw a circle with center V and radius VS. This circle will intersect the radius VS at two points, label these points as R and T.
Draw segments RT and RS to complete the equilateral triangle RST.
Your construction should show a circle with center V and an inscribed equilateral triangle RST.
To learn more about circle visit:
https://brainly.com/question/24375372
#SPJ1

Find the general solution of the given differential equation and then find the specific solution satisfying the given initial conditions.
Y^2dy/dx − xy^3 = 2x given. y(0)=2
Answers
The general solution of the given differential equation is y = (x ± √(x^2 + 2e^2x)) / e^x, and the specific solution satisfying the initial condition y(0) = 2 is y = 0.
To solve the given differential equation, let's rewrite it in a more standard form:
y^2 * dy/dx - xy^3 = 2x
First, let's separate the variables by moving all the terms involving y to one side and all the terms involving x to the other side:
y^2 * dy - y^3 * dx = 2x * dx
Next, we divide both sides of the equation by y^2 * dx to isolate dy:
dy/dx - (y^3 / y^2) = (2x / y^2) * dx
Simplifying the expression on the left side:
dy/dx - y = (2x / y^2) * dx
Now, we can see that this is a first-order linear ordinary differential equation of the form dy/dx + P(x) * y = Q(x), where P(x) = -1 and Q(x) = (2x / y^2).
The integrating factor for this equation is given by exp(∫P(x)dx) = exp(-∫dx) = exp(-x) = 1/e^x.
Multiplying both sides of the equation by the integrating factor, we get:
(1/e^x) * dy/dx - (1/e^x) * y = (2x / y^2) * (1/e^x)
This can be rewritten as:
d/dx (y/e^x) = (2x / y^2) * (1/e^x)
Integrating both sides with respect to x, we obtain:
∫d/dx (y/e^x) dx = ∫(2x / y^2) * (1/e^x) dx
Integrating the left side gives us y/e^x, and integrating the right side requires integration by parts. Applying integration by parts once, we have:
y/e^x = ∫(2x / y^2) * (1/e^x) dx
= -2∫x * (1/y^2) * (1/e^x) dx
= -2 * (x * (-1/y^2) * (1/e^x) - ∫(-1/y^2) * (1/e^x) dx)
= 2x/y^2 * (1/e^x) + 2∫(1/y^2) * (1/e^x) dx
Continuing with the integration by parts, we integrate ∫(1/y^2) * (1/e^x) dx:
y/e^x = 2x/y^2 * (1/e^x) + 2 * (1/y^2) * (1/e^x) - 2∫(d/dx(1/y^2)) * (1/e^x) dx
Differentiating 1/y^2 with respect to x, we get:
d/dx(1/y^2) = (-2/y^3) * (dy/dx)
Substituting this back into the equation, we have:
y/e^x = 2x/y^2 * (1/e^x) + 2 * (1/y^2) * (1/e^x) + 2∫(2/y^3) * (1/e^x) * (1/e^x) dx
Simplifying the equation further, we obtain:
y/e^x = 2x/y^2 * (1/e^x) + 2/y^2 * (1/e^x) + 2∫(2/y^3) *
(1/e^(2x)) dx
To solve the integral on the right side, we can make the substitution u = e^x:
du/dx = e^x
Rearranging the equation, we have dx = du/e^x = du/u.
Substituting u = e^x and dx = du/u into the integral, we get:
2∫(2/y^3) * (1/u^2) du
This integral can be easily evaluated as:
4∫(1/y^3u^2) du = -4/y^3u
Substituting u = e^x back into the equation, we have:
4∫(1/y^3e^2x) dx = -4/y^3e^x
Substituting this result back into the equation, we get:
y/e^x = 2x/y^2 * (1/e^x) + 2/y^2 * (1/e^x) - 4/y^3e^x
Combining the terms on the right side, we have:
y/e^x = (2x + 2 - 4/y) * (1/y^2) * (1/e^x)
Multiplying through by y^2 * e^x, we obtain:
y * e^x = (2x + 2 - 4/y) * (1/e^x)
Expanding the right side, we have:
y * e^x = (2x/e^x + 2/e^x - 4/y * 1/e^x)
Simplifying further:
y * e^x = 2x/e^x + 2 - 4/(y * e^x)
Now, let's solve for y. Multiplying through by y * e^x:
y^2 * e^x = 2xy + 2ye^x - 4
Rearranging the terms:
y^2 * e^x - 2xy - 2ye^x = -4
This is a quadratic equation in y. To solve for y, we can use the quadratic formula:
y = (-b ± √(b^2 - 4ac)) / 2a
Comparing the equation to the standard quadratic form, we have:
a = e^x
b = -2x
c = -2e^x
Substituting these values into the quadratic formula, we get:
y = (-(-2x) ± √((-2x)^2 - 4(e^x)(-2e^x))) / (2(e^x))
Simplifying further:
y = (2x ± √(4x^2 + 8e^2x)) / (2e^x)
= (x ± √(x^2 + 2e^2x)) / e^x
This is the general solution of the given differential equation. Now, let's find the specific solution satisfying the initial condition y(0) = 2.
Substituting x = 0 into the general solution, we have:
y(0) = (0 ± √(0^2 + 2e^2*0)) / e^0
= (0 ± √(0 + 0)) / 1
= 0 ± 0
= 0
Therefore, the specific solution satisfying the initial condition y(0) = 2 is y = 0.
Learn more about variables at: brainly.com/question/29583350
#SPJ11
If Leonel has an eye level of 5 feet above the ground and he is standing 40 feet from a flagpole that is 32 feet tall, then what is the angle of elevation? Round to the nearest whole number.
A. 27
B. 42
C. 200
D. 34
Answers
Answer:
Have a good day people
Step-by-step explanation:
In kite PQRS, m_OPO = 50° and m_ORO = 70°. Find m2PSR

Answers
Answer:
m<PSR = 60°
Step-by-step explanation:
Given:
m<OPQ = 50°
m<ORQ = 70°
Required:
m<PSR
Solution:
m<PQR + m<OPQ + m<ORQ = 180° (Sum of triangle)
m<PQR + 50 + 70 = 180 (Substitution)
m<PQR + 120 = 180
m<PQR = 180 - 120
m<PQR = 60°
One of the properties of a kite states that the angles where the unequal sides meets are congruent to each other. Therefore:
m<PSR = m<PQR
m<PSR = 60° (substitution)
you have a coin and you toss it 8 times. how many possible outcomes we can have if the outcome should have a head in its third and fifth tosses.
Answers
The possible outcomes should have a head in its third and fifth tosses is 219, according to the question.
What do you mean by probability?
The area of mathematics known as probability deals with numerical representations of the likelihood that an event will occur or that a statement is true. An event's probability is a number between 0 and 1, where, roughly speaking, 0 denotes the event's impossibility and 1 denotes certainty.
According to the given question,
We can toss it 8 times,
Exactly three heads (hence, exactly 5 tails), no fewer, no more. So there are eight coins, and we need to compute how many ways we can choose three to be heads:
(83)=8!/3!5!=56
At least three heads (hence, at most 5 tails): here we count sequences with exactly 3 heads, and also count sequences with more than three heads. What doesn't count are those sequences containing (zero heads, exactly one head, or exactly two heads). We could compute this as
(83)+(84)+⋯+(88)
But it would be far easier to compute its equivalent, by subtracting from 256 the number of sequences with no head, only one head, and only 2 heads:
256−((8/0)+(8/1)+(8/2))=256−(1+8+28)=219
Therefore, the possible outcomes should have a head in its third and fifth tosses is 219.
To learn about probability, visit:
https://brainly.com/question/11234923?referrer=searchResults
#SPJ4
Which is different? Write "both" inequalities.
A. k is less than or equal to -3 B. k is no more than -3
C. k is at most -3
D. k is at least -3
The inequality that represents the different sentence is __ .
The inequality that represents the sentences that are alike is __ .
(I’m doing this work on big ideas math btw)
Answers
Answer:
c
Step-by-step explanation:
The answers for the given problem can be stated as, "The inequality that represents the different sentence is represented by option (D)."And, "The inequality that represents the sentences that are alike is represented by options (A), (B) and (C) respectively."
What is linear inequality?Linear inequality refers to the relation between a linear algebraic expression to some known value that contains inequality sign.
Unlike a linear equation it can have a range of values inside an interval.
The expression for inequality for all the options are written one by one as follows,
(A) k is less than or equal to -3.
=> k ≤ -3.
(B) k is no more than -3
=> k ≤ -3
(C) . k is at most -3
=> k ≤ -3
(D) k is at least -3
=> k ≥ -3
Hence, options (A), (B) and (C) represents like while (D) represents different inequality.
To know more about linear inequality click on,
https://brainly.com/question/11897796
#SPJ2