Is x5+5x a like term
Answers
Explanation
We are given the following:
\(x5+5x\)We are required to determine whether or not the expression is a like term.
We know that like terms are terms that have the same variables and powers. The coefficients do not need to match.
Hence, they are like terms. This is because they have the same variable x and the same power of 1.
Related Questions
7. Newton buys a board game for $9.99
and a pack of trading cards for $2.99.
He gives the cashier a $20 bill. How
much change does he receive?
AWNSER ASAPP
Answers
Answer: Hello, there! Your Answer is Below^^
7.O2 Would be The Correct Answer.
Step-by-step explanation:
So I Subtracted 20 - 12.98 And Got the Answer $ 7.02
To Add Or subtract Decimals Here's what you can do to find your Answer
Line up the numbers vertically so that the decimal points all lie on a vertical line.
Add extra zeros to the right of the number so that each number has the same number of digits to the right of the decimal place. Step 3: Subtract the numbers as you would whole numbers.
Hope this Helps!!
Have a great day!!!
Pls help
Find the surface area of the composite figure.

Answers
Answer:
644 cm³
Step-by-step explanation:
Surface area of the composite figure = (surface area of the upper cuboid - base area of upper cuboid) + (surface area of the lower cuboid - base area of the upper cuboid)
✔️Surface area of upper cuboid = 2(LW + LH + WH)
L = 3
W = 3
H = 8
Surface area of upper cuboid = 2(3*3 + 3*8 + 3*8) = 2(9 + 24 + 24) = 114 cm²
✔️Surface area of Surface area of lower cuboid = 2(LW + LH + WH)
L = 12
W = 10
H = 7
Surface area of lower cuboid = 2(12*10 + 12*7 + 10*7) = 2(120 + 84 + 70) = 548 cm²
✔️Base area of upper cuboid = L*W
L = 3
W = 3
Base area = 3*3 = 9 cm²
✅Surface area of the composite figure = (114 - 9) + (548 - 9) = 105 + 539 = 644 cm³
The distance, in feet, two boys travel per second on a treadmill is shown to the left. Which comparison is accurate?
Xavier is traveling at 1.5 feet per second.
Moises is going faster than Xavier.
The difference in their rates of change is 1 foot per second.
If both boys remain on the treadmill for 10 minutes, Xavier will have traveled a greater distance. (a straight up answer)
Answers
Answer:
Step-by-step explanation:
D is correct
Answer: D
Step-by-step explanation:
present ages of two children are 2 and 5 years the rspectively. After how long will the sum of their square ages be 45.
Answers
Using the concept of word problems and quadratic equation it will take 1 year until the sum of square of their ages be 45.
Calculating the duration to get the sum to 45Word problems are mathematical problems that are delivered in ordinary words, instead of mathematical symbols.
Part of the problem with dealing with word problems that they first need to be translated into mathematical equations, and then the equations need to be solved.In this problem;
let x represent the number of years from now when the sum of square of their respective age will be
45.(x + 2)² + (x + 5)² = 45
Expanding the brackets;
x² + 4x + 4 + x² + 10x + 25 = 45
2x² + 14x + 29 = 45
2x² + 14x + 29 - 45 = 0
2x² + 14x - 16 = 0
Solving the quadratic equation for x;
x = 1, x = -8
Taking the positive value, the value of x is 1
Learn more on age word problems here;
https://brainly.com/question/17043336
#SPJ1
A salesperson uses random digit dialing to call people and try to interest them in applying for a charge card for a large department store chain. From past experience, she is successful on 2% of her cals. in typical working, she makes 50 calls. Let X be the number of calls on which she is unsuccessful.
a. This is binomial distribution. Explain using the BINS method why this is so.
b. Find the mean and standard deviation of X. Leave answer to 4 d.p
c. Find the probablity of P(X>or equal to 48)
Answers
Answer:
a)
In this question, for each call, there are only two possible outcomes, either it is successful, or it is not, so binary outcomes. For each call, the probability of a success or failure is the same, which means that the trials are independent, having the same value of p. And the number of trials, which is 50, is fixed. This means that this is a binomial distribution.
b) The mean is 1 and the standard deviation is 0.9899.
c) \(P(X \geq 48) = 0\)
Step-by-step explanation:
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
In which \(C_{n,x}\) is the number of different combinations of x objects from a set of n elements, given by the following formula.
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
And p is the probability of X happening.
The expected value of the binomial distribution is:
\(E(X) = np\)
The standard deviation of the binomial distribution is:
\(\sqrt{V(X)} = \sqrt{np(1-p)}\)
From past experience, she is successful on 2% of her calls.
This means that \(p = 0.02\)
50 calls.
This means that \(n = 50\)
a. This is binomial distribution. Explain using the BINS method why this is so.
BINS: Binary outcomes, Independent Trials, n is fixed, and same value of p for all trials.
In this question, for each call, there are only two possible outcomes, either it is successful, or it is not, so binary outcomes. For each call, the probability of a success or failure is the same, which means that the trials are independent, having the same value of p. And the number of trials, which is 50, is fixed. This means that this is a binomial distribution.
b. Find the mean and standard deviation of X.
The mean is:
\(E(X) = np = 50*0.02 = 1\)
The standard deviation is:
\(\sqrt{V(X)} = \sqrt{np(1-p)} = \sqrt{50*0.02*0.98} = 0.9899\)
The mean is 1 and the standard deviation is 0.9899.
c. Find the probablity of P(X>or equal to 48)
This is:
\(P(X \geq 48) = P(X = 48) + P(X = 49) + P(X = 50)\)
In which
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(P(X = 48) = C_{50,48}.(0.02)^{48}.(0.98)^{2} \approx 0\)
\(P(X = 49) = C_{50,49}.(0.02)^{49}.(0.98)^{1} \approx 0\)
\(P(X = 50) = C_{50,50}.(0.02)^{50}.(0.98)^{0} \approx 0\)
So
\(P(X \geq 48) = 0\)
what is the measure of x

Answers
Answer:
x = 9 inches
Step-by-step explanation:
You want the value of x in the similar triangles shown.
ProportionCorresponding sides are proportional. This means the ratio of the horizontal side of the triangle to the vertical side is the same for both.
6/4 = (6+x)/10
15 = 6 +x . . . . . . . . multiply by 10
9 = x . . . . . . . . . subtract 6
The measure of x is 9 inches.
__
Additional comment
You could also write the proportion ...
6/4 = x/(10 -4)
x = 36/4 = 9 . . . . . . . multiply by 6
You can see this if you draw a horizontal line through the figure at the top of the side marked 4 in.
<95141404393>
Answer the photo please and do my other ones

Answers
Answer:
C
Step-by-step explanation:
If you were to put the number of turkey out in order from least to greatest, the median is 12. Doing the same thing to the ham, the median is 9.
Subtracting Turkey (12) from Ham (9) your answer is C, or 3.
Define random error. Define random error. Random error has values that are consistent with one another. Random error has no probability of being too high or too low. Random error is an error that tends to be either too high or too low. Random error has an equal probability of being too high or too low. Random error has values that are close to the true value.
Answers
Define random error: B) Random error is an error that tends to be either too high or too low.
WHAT IS RANDOM ERRORRandom error, is an error caused by factors that cannot be predicted, you could even say that these factors seem temporary.
So, it is very difficult to predict, because it is still random. One might even say, this random error occurred, while the test was being conducted. Even worse, random errors do not have to occur in the first test, it could be in the second or third test and so on.
Random error is a very small and dissimilar effect in each test implementation, for example the effect of fluctuations in the voltage, temperature or humidity conditions of the accommodation and test environment.
Learn more about random error at
https://brainly.com/question/29445533.
#SPJ4
The map shows an obstacle course at a school fair. The units are given in yards.
What is the total distance of
the obstacle course?
? yards
Start
(-40, -10)
Tire
Race
(-40, -30)
Finish
(10, 20)
Monkey
Bars
(40,20)
Rope
Climb
(40,-30)
Answers
The total distance of the obstacle course can be calculated by finding the distance between each pair of consecutive points and adding them up. The distance between two points (x1, y1) and (x2, y2) can be calculated using the formula: distance = sqrt((x2 - x1)^2 + (y2 - y1)^2).
Using this formula, we can calculate the distances between each pair of consecutive points as follows:
Start to Tire Race: distance = sqrt((-40 - (-40))^2 + (-30 - (-10))^2) = 20 yards
Tire Race to Rope Climb: distance = sqrt((40 - (-40))^2 + (-30 - (-30))^2) = 80 yards
Rope Climb to Monkey Bars: distance = sqrt((40 - 40)^2 + (20 - (-30))^2) = 50 yards
Monkey Bars to Finish: distance = sqrt((10 - 40)^2 + (20 - 20)^2) = 30 yards
Adding up all these distances, we get a total distance of 20 + 80 + 50 + 30 = 180 yards for the obstacle course.
Consider this function.
f(x) = |x – 4| + 6
If the domain is restricted to the portion of the graph with a positive slope, how are the domain and range of the function and its inverse related?
Answers
If we restrict the domain of the function to the portion of the graph with a positive slope, the domain of the inverse function will be the range of the original function for values of x greater than 4, and its range will be all real numbers greater than or equal to 4.
The given function f(x) = |x – 4| + 6 is a piecewise function that contains an absolute value. The absolute value function has a V-shaped graph, and the slope of the graph changes at the point where the absolute value function changes sign. In this case, that point is x=4.
If we restrict the domain of f(x) to the portion of the graph with a positive slope, we are essentially considering the piece of the graph to the right of x=4. This means that x is greater than 4, or x>4.
The domain of the inverse function, f⁻¹(x), will be the range of the original function f(x) for values of x greater than 4. This is because the inverse function reflects the original function over the line y=x. So, if we restrict the domain of f(x) to values greater than 4, the reflected section of the graph will be the range of f⁻¹(x).
The range of f(x) is all real numbers greater than or equal to 6 because the absolute value function always produces a positive or zero value and when x is greater than or equal to 4, we add 6 to that value. The range of f⁻¹(x) will be all real numbers greater than or equal to 4, as this is the domain of the reflected section of the graph.
for more such questions on domain
https://brainly.com/question/2264373
#SPJ8
Use the given measurements to solve the triangle. Round lengths of sides lo the nearest tenth and angle measures to the nearest degree. a = 500,b = 300 The measure of angle B is approximately (Round to the nearest degree:)
Answers
Therefore, the measure of angle B in the given triangle is approximately 59°.
What is triangle?A triangle is a polygon with three sides and three angles. It is a two-dimensional geometric shape that can be formed by connecting three points that are not collinear (lying on the same straight line). The three points of a triangle are called its vertices, and the line segments connecting them are its sides. The sides of a triangle can have different lengths, and the angles between them can have different measures. In a triangle, the sum of the interior angles is always 180°. This is known as the angle sum property of triangles.
Here,
To solve for the measure of angle B in the given triangle, we can use the inverse tangent function, which is commonly denoted as tan⁻¹ or arctan. Specifically, we can use the following formula:
tan(B) = opposite/adjacent
where B is the angle we want to find, and opposite and adjacent are the lengths of the sides of the triangle that form the angle B.
In this case, we know that side a is opposite to angle B, and side b is adjacent to angle B. So we have:
tan(B) = a/b = 500/300 = 5/3
To find the value of angle B, we can take the inverse tangent of both sides of the equation, using a calculator or a table of trigonometric functions. We get:
B = tan⁻¹(5/3) ≈ 59°(rounded to the nearest degree)
To know more about triangle,
https://brainly.com/question/28600396
#SPJ1
If a cube has volume 125cm³, find the height of the cube.
Answers
Answer:
height = 5 cm
Step-by-step explanation:
a cube has congruent sides (s)
the volume (V) of a cube is calculated as
V = s³
given V = 125 , then
s³ = 125 ( take cube root of both sides )
\(\sqrt[3]{s^3}\) = \(\sqrt[3]{125}\) = \(\sqrt[3]{5^3}\)
s = 5
then height = 5 cm
You and your friend have a bet. If you roll a standard six-sided die and get a 4 and then roll it again and get a 6, she will give you $100. You must roll a 4 and a 6 to win. What is the percentage chance you will win this bet?
Answers
Answer: 3%
Step-by-step explanation:
first roll 1 out of 6 chance or 16%
second roll is also 1 out of 6 chance or 16%
Mulitple .16 by .16 to get .0256 rounded to whole percentage 3%
We have 2 squares. One square is shaded 2/12 and the other shaded square in the diagram is 2/15 shaded. How much of the total diagram is shaded?
A.0.148
B.0.148 repeated
C. 0.3
D.0.3 repeated
Answers
Answer: The answer to your question is C. Brainliest?
Step-by-step explanation:
For the first square, we can multiply both the numerator and denominator by 5 to get an equivalent fraction with a denominator of 60:
2/12 = (2 x 5) / (12 x 5) = 10/60
For the second square, we can multiply both the numerator and denominator by 4 to get an equivalent fraction with a denominator of 60:
2/15 = (2 x 4) / (15 x 4) = 8/60
Now, we can add the two fractions:
10/60 + 8/60 = 18/60
Simplifying this fraction by dividing both numerator and denominator by 6, we get:
18/60 = 3/10
Therefore, the total shaded area in the diagram is 3/10 or 0.3 in decimal form.
The answer is C. 0.3.
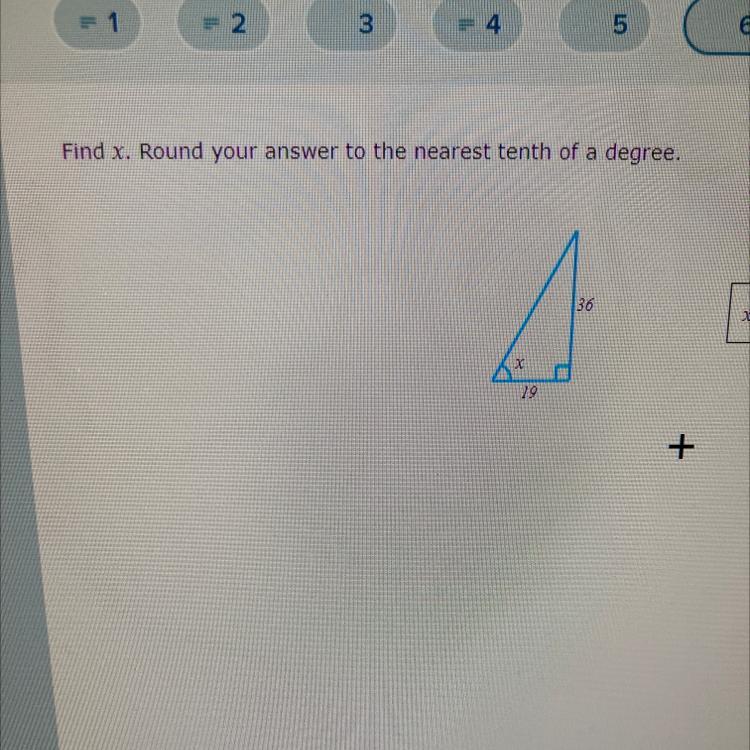
Find x. Round your answer to the nearest tenth of a degree.
36
X
19
+
Answers
Answer: 36.9
Step-by-step explanation:
True or False: Slope is always rise over run.
Answers
Answer:
The formula for slope is sometimes referred to as "rise over run", because the fraction onsists of the "rise" (being the change in y, going up or down) divided by the "run" (being the change in x, going from left to the right).
Step-by-step explanation:
Answer:
Good sir/madam, in a fraction, it is always rise over run.
I can buy candy bars for 50 cents each how much would 32 candy barks cost
Answers
Answer:
50*32=16.00
Step-by-step explanation:
Write the relation as a set of ordered pairs.
a. ordered pairs: {(-3, -6), (0, 0), (3, 6)}
b. ordered pairs: {(-6, -3), (0, 0), (6,3)}
c. ordered pairs: {(-6,-3), (0, 0), (3, 6)}
d. ordered pairs: {(-3, -6), (0, 0), (6,3)}

Answers
Answer:
option (d) is correct.
Step-by-step explanation:
Given the table
x -3 0 3
y -6 0 6
An ordered pair (x, y) is a composition of the x-coordinate and y-coordinate.
For example, the ordered pair (1, 2) is a composition of the x-coordinate i.e. x = 1 and y-coordinate i.e. y = 2.
The relation can be determined by converting all the points in the table via the ordered pairs and combining all of them such as ordered pairs:
{(-3, -6), (0, 0), (3, 6)}
Therefore, option (d) is correct.
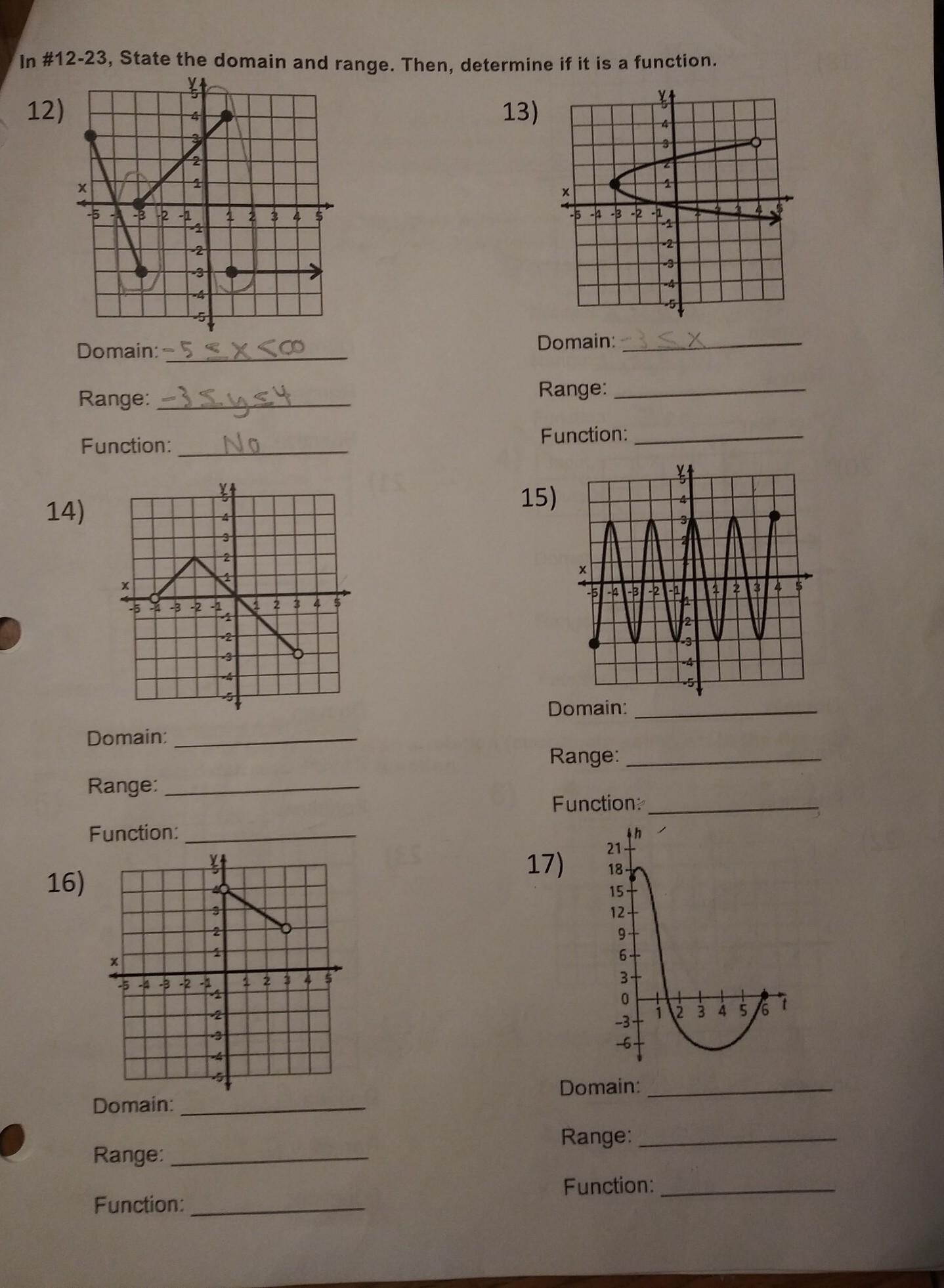
Can someone please help me with #13-17?Please,I really need the help.I have been stuck on this for 1 hour and still don't know what to do.
Answers
Problem 13
The domain is the set of allowed x inputs. Locate the left-most point. From there, draw a vertical line until you reach the x axis. You should reach x = -3. This is the smallest x value in the domain, and it is included due to the closed circle here. We cannot repeat this for the right-most point because there is no right-most point. The arrow shows the curve goes on forever to the right. So infinity is the largest x value.
In short, x is between -3 and infinity and we write it like so: \(-3 \le x < \infty\)
You could write it also as \(-3 \le x\) or \(x \ge -3\), but the first notation mentioned with infinity seems to be the most descriptive in my opinion. That first notation also can be readily converted to the interval notation \([-3, \infty)\). The square bracket says "include -3" while the curved parenthesis says we exclude infinity. We can never reach infinity, so there's no way to include it. It's not a number. It's a concept.
As for the range, we will do the same idea as before. This time we'll look to the y axis. The highest we can go is y = 3 and we can't actually reach this value due to the open hole here. There is no smallest y value because of the arrow on the curve pointing downward forever.
Therefore, the range is the set of y values between negative infinity and 3, excluding both endpoints. We would say \(-\infty < y < 3\)
Now to the question whether this is a function or not. We can use the vertical line test to check. If it is possible to draw a single vertical line through more than one point on the curve, then we do not have a function. We can see that such a thing would happen for this curve. For instance, draw a vertical line through x = 0 (aka the y axis itself) and we see that two points are on the curve at the same time here. The input x = 0 leads to more than one output. This is one example of infinitely many to see why we do not have a function.
---------------------------
Answers:Domain: \(-3 \le x < \infty\)Range: \(-\infty < y < 3\)Function: No===========================================================
Problem 14
The inputs x span from x = -4 to x = 3, excluding both endpoints due to the open holes. They can be thought of as potholes on the road you don't want to drive on (simply because that portion of the road doesn't even exist).
Therefore, the domain is \(-4 < x < 3\)
The range is \(-3 < y \le 2\) because the lowest y can get is y = -3 and the highest it can get is y = 2. However, we exclude y = -3 itself because of the open hole. We include y = 2.
In contrast to problem 13, we have a function this time. It is impossible to draw a single straight vertical line through more than one point on this V shape curve. This graph passes the vertical line test.
---------------------------
Answers:Domain: \(-4 < x < 3\)Range: \(-3 < y \le 2\)Function: Yes===========================================================
Problem 15
The left-most point occurs when x = -5 and the right-most point is when x = 4. We include both endpoints since there are no open holes here. Every bit of road is defined. The domain is \(-5 \le x \le 4\)
Locate any of the many lowest valley points. Draw a horizontal line until you reach the y axis. You should reach y = -3. Repeat for one of the highest points and you'll get to y = 3. The range is \(-3 \le y \le 3\)
Like problem 14, this graph passes the vertical line test. Therefore, we have a function. Any x input, in the domain mentioned, produces exactly one and only one y output. The key here is "in the domain mentioned". We cannot plug in x values outside this domain.
---------------------------
Answers:Domain: \(-5 \le x \le 4\)Range: \(-3 \le y \le 3\)Function: Yes===========================================================
Problem 16
There's not much different from something like problem 14. The domain here is \(0 < x < 3\) and the range is \(2 < y < 4\)
We have a function because this graph passes the vertical line test.
---------------------------
Answers:Domain: \(0 < x < 3\)Range: \(2 < y < 4\)Function: Yes===========================================================
Problem 17
Same idea as before. The left-most point occurs when x = 0 and the right-most point is when x = 6. Therefore \(0 \le x \le 6\) is our domain here.
The highest point seems to occur at y = 18 based on what the graph says. The lowest point is perhaps when y = -9. These two y values are estimations. So it's possible the range is \(-9 \le y \le 18\)
We have another function here because this curve passes the vertical line test. Only problems 12 and 13 were a non-function. Everything else is a function.
---------------------------
Answers:Domain: \(0 \le x \le 6\)Range: \(-9 \le y \le 18\) Function: YesUse the following bond listing for Pacific Bell to answer the following:
A 5-column table with 1 row. Column 1 is labeled Bonds with entry PacBell 6 and StartFraction 5 Over 8 EndFraction 34. Column 2 is labeled current yield with entry 6.55. Column 3 is labeled Volume with entry 5. Column 4 is labeled Close with entry 99 and one-fourth. Column 5 is labeled net change with entry + StartFraction 1 Over 8 EndFraction.
What was the closing price of the bond? What was the dollar amount?
a. 106 5/8; $966
b. 6 5/8; $6625
c. 99 1/4; $993.45
d. 99 1/4; $992.50
Answers
Answer:
b.
$66.25
Step-by-step explanation:
just did the test
Examine the diagram.
Complete the statement by typing the letter of the angle.
m______= 54°

Answers
Answer:
m∠B=54°
Step-by-step explanation:
use the fact that the sum of angles in a triangle is 180°
2x+7+4x-10+7x-25 =180
combine like terms
13x -28 =180
13x = 180+28
x= 208/13= 16
∠B = 4x-10 = 4*16 -10 = 64-10= 54°
You run around all 4 bases on the baseball field. Your friend runs a 100-yard dash.
Who runs a greater distance? How much greater?
Answers
Explanatory Answer:
To answer this question, we need to know the distances involved in running around all 4 bases on a baseball field and running a 100-yard dash.
The distance between each base on a baseball field is 90 feet, or approximately 27.4 meters. Running around all 4 bases involves a total distance of 360 feet, or approximately 109.7 meters.
A 100-yard dash is equivalent to running 300 feet, or approximately 91.4 meters.
Therefore, running around all 4 bases on a baseball field involves a greater distance than running a 100-yard dash. The difference in distance is:
360 feet - 300 feet = 60 feet
or
109.7 meters - 91.4 meters = 18.3 meters
So running around all 4 bases on a baseball field involves 60 feet or 18.3 meters more distance than running a 100-yard dash.
Name a street that is perpendicular to Hwy 64/40 . Can you help with all these questions

Answers
Answer:
no puedo alludar te perdón
In order for you to carry a bag on the plane, it must fit inside the carry-on Baggage Check Box. The carry-on Baggage Check Box has dimensions of approximately 22 inches x 14 inches x 9 inches. Your black bag has a height of 18 inches, a depth of 12 inches and a width of 8 inches. Your blue bag has a height of 18 inches, a depth of 15 inches and a width of 10 inches.
What is the volume of the Carry-on Baggage Check Box?
22×14x9= 2772 inches3
What is the volume of the black bag?
What is the volume of the blue bag?
Which bag will definitely fit in the Check Box? Explain.
You notice these two old suitcases stacked in the closet. The smaller suitcase is 25 inches x 8 inches x 9 inches and the larger suitcase is 75 inches x 20 inches x 18 inches.
The bigger suitcase is how many times larger than the smaller suitcase? HINT: You will need to divide on this one.
You decide to use the larger suitcase to transport rectangular prism watermelons back home. The watermelons are about 720 cubic inches. If one of the watermelons is about 10 inches long and 9 inches wide, about how tall would it be? (Hint: V=LxWxH, so plug in 720=10x9xH and solve for H).
If the watermelons are about 720 cubic inches, what is the MAXIMUM amount of watermelons you’ll be able to bring home in your larger suitcase, assuming all you have in the suitcase is the watermelons. (Hint: Divide the larger suitcase volume and the volume of the watermelon).
Answers
1. The volume of the black bag is 1728 cubic inches. 2. The volume of the blue bag is 2700 cubic inches. 3. The black bag will fit in the Check Box. 4. The bigger suitcase is 27 times larger than the smaller suitcase.
What is volume?Volume, which is commonly expressed in cubic units, is the amount of space occupied by a three-dimensional object. By multiplying an object's length, breadth, and height, as well as other formulas depending on the shape of the object, one can get the volume of the thing. Volume is a key concept in many practical applications, including calculating container capacity, constructing structures, and estimating the amount of material required for a construction project. Volume is utilised in many branches of mathematics, science, and engineering.
For the given dimensions of the bags we have:
1. The volume of the black bag is:
18 x 12 x 8 = 1728 cubic inches
2. The volume of the blue bag is:
18 x 15 x 10 = 2700 cubic inches
3. The black bag will definitely fit in the Check Box because its volume of 1728 cubic inches is less than the volume of the Check Box, which is 2772 cubic inches.
4. The ratio of bigger suitcase to smaller suitcase is:
75 x 20 x 18 = 27000 cubic inches
25 x 8 x 9 = 1800 cubic inches
27000 / 1800 = 27
The bigger suitcase is 27 times larger than the smaller suitcase.
5. Now, if the watermelons is about 10 inches long and 9 inches wide, then its height would be:
720 = 10 x 9 x H
720 = 90H
H = 8 inches
The maximum amount of watermelons that can fit are:
27000 / 720 = 37.5 watermelons = 37 watermelons.
Learn more about volume here:
https://brainly.com/question/1578538
#SPJ1
You say goodbye to your friend at the intersection of two perpendicular roads. At time t=0 you drive off North at a (constant) speed v and your friend drives West at a (constant) speed w. You badly want to know: how fast is the distance between you and your friend increasing at time t? Enter here the derivative of the distance from your friend with respect to t: __________. Being scientifically minded you ask yourself how does the speed of separation change with time. In other words, what is the second derivative of the distance between you and your friend? __________. Suppose that after your friend takes off (at time t=0) you linger for an hour to contemplate the spot on which your friend was standing. After that hour you drive off too (to the North). How fast is the distance between you and your friend increasing at time t (greater than one hour)? __________. Again, you ask what is the second derivative of your separation: ____________.
Answers
Answer:
Let x be the distance traveled by you to the north and y be the distance traveled by your friend to the west. Let d be the distance between you and your friend at time t. Then, we have:
d^2 = x^2 + y^2
Taking the derivative of both sides with respect to time, we get:
2d (dd/dt) = 2x(dx/dt) + 2y(dy/dt)
Simplifying this expression, we get:
dd/dt = (x(dx/dt) + y(dy/dt)) / d
Since you are driving north at a constant speed v and your friend is driving west at a constant speed w, we have:
dx/dt = v and dy/dt = -w
Substituting these values and simplifying, we get:
dd/dt = (v^2 + w^2)^0.5
Therefore, the speed of separation between you and your friend at time t is the square root of the sum of the squares of your speeds.
To find the second derivative of the distance between you and your friend, we take the derivative of dd/dt with respect to time:
d^2d/dt^2 = (v dv/dt + w dw/dt) / (v^2 + w^2)^0.5
Since v and w are constant, their derivatives with respect to time are zero, so the second derivative of the distance between you and your friend is zero.
Suppose you wait for an hour (i.e., t = 1 hour) before driving off to the north. Then, at time t > 1 hour, the distance between you and your friend is given by:
d = (vt)^2 + ((t-1)w)^2)^0.5
Taking the derivative of both sides with respect to time, we get:
dd/dt = 2v^2t / (2((vt)^2 + ((t-1)w)^2)^0.5)
Simplifying this expression, we get:
dd/dt = v / ((v^2 + ((t-1)w)^2)^0.5)
Therefore, the speed of separation between you and your friend at time t (greater than one hour) is given by v divided by the square root of the sum of the squares of your speed and your friend's speed.
The second derivative of the distance between you and your friend is given by:
d^2d/dt^2 = -vw(t-1) / ((v^2 + ((t-1)w)^2)^1.5)
In the first 4 games of the season, a soccer team scored a total of 10 goals. If this trend
continues, how many goals will the teams score in the 18 remaining games of the season?
Answers
Answer:
they would score 180 goles
Step-by-step explanation:
a. In the general education course requirement at a college, a student needs to choose one each from social sciences, humanities, natural sciences, and foreign languages. There are 5 social science courses, 4 humanity courses, 4 natural science courses, and 3 foreign language courses available for general education. How many different ways can a student choose general education courses from these 4 areas?
Answers
Using the Fundamental Counting Theorem, there are 240 ways to choose general education courses from these 4 areas.
What is the Fundamental Counting Theorem?It is a theorem that states that if there are n things, each with \(n_1, n_2, \cdots, n_n\) ways to be done, each thing independent of the other, the number of ways they can be done is:
\(N = n_1 \times n_2 \times \cdots \times n_n\)
Considering the number of options for each course, the parameters are given as follows:
\(n_1 = 5, n_2 = 4, n_3 = 4, n_4 = 3\).
Hence the number of ways is given by:
N = 5 x 4 x 4 x 3 = 240.
More can be learned about the Fundamental Counting Theorem at https://brainly.com/question/24314866
#SPJ1
what is the correct rational expression of the phrase "the quotient of 2x and 3y ?
Answers
Answer:
\(Expression= \frac{2x}{3y}\)
Step-by-step explanation:
Required
Determine the quotient of 2x and 3y
Quotient means division.
Take for instance; quotient of 1 and 2 is \(\frac{1}{2}\) and so on.
So, the given statement can then be interpreted to mean 2x divided by 3x
Using the above analysis, we have the following representations.
\(Expression= \frac{2x}{3y}\)
Some factors need to be controlled to keep this test fair. name two of them….

Answers
Two factors that need to be controlled to keep this test fair are the temperature and the sample volume.
What are the control variables?The control variables are those variables that should be kept constant in order to avoid interfering with the free flow of the experiment.
For the provided test, it is important that the temperature of the environment where the test sample is kept is controlled throughout the duration of the experiment so that some results are not affected by this. Also, the sample volume should be controlled for fair outcomes.
Learn more about control variables here:
https://brainly.com/question/28077766
#SPJ1
Which two points are on the line represented by this equation
y = x - 6
Answers
Answer:
(0, -6) , (6, 0)
Step-by-step explanation:
it could be (0, -6) or (6,0)