is 4 a factor of 72
Answers
Answer:
Yes
Step-by-step explanation:
Yes. 72 divided by 4 would be 18, so it is a factor
Answer:
Yes
Step-by-step explanation:
Yes because 4 x 18 = 72
72 divided by 18 = 4
I know this because if you multiply 4 x 18 you will get 72. To check you can do the inverse operation, which is division, so with that being said, 72 divided by 18 = 4.
I explained to so you can have a better understanding. Have a great day!
Related Questions
What is a name for the marked angle?

Answers
Answer: \(\angle BAD\)
Reason:
The arc goes from ray AB to ray AD. The two rays join at angle A which is the vertex point. When naming an angle, always use the vertex point in the middle. The order of the other two letters does not matter.
We could name this angle as \(\angle BAD\) or \(\angle DAB\) to mean the same exact thing. All that matters is that "A" is in the middle.
Ignore point C, and ignore ray AC entirely.
Answer:
(b) ∠BAD
Step-by-step explanation:
An angle can be named by the names of three points. The first point is on one of the rays that form the angle; the second point is the vertex; the third point is on the other ray.
Apparently the "marked" angle is identified by the arc extending from ray AB to ray AD. Point A is the vertex of the angle, so one possible name for it is ...
∠BAD
It can also be called
∠DAB
two similar solids have a scale factor of 3 4 if the volume of the smaller solid is 54 what is volume of the larger solid
Answers
From the given information, upon calculation, the volume of the larger solid is 192.
When two similar solids have a scale factor of 3:4, it means that the corresponding lengths of the two solids are in a ratio of 3:4. Since volume is a three-dimensional measurement, it depends on the cube of the length. Therefore, the volume of the larger solid will be the cube of the scale factor multiplied by the volume of the smaller solid.
Given that the volume of the smaller solid is 54, we can calculate the volume of the larger solid as follows:
Volume of the smaller solid = 54
Scale factor = 3:4
Volume of the larger solid = (scale factor^3) * Volume of the smaller solid
= (4/3)^3 * 54
= (64/27) * 54
= 192
Therefore, the volume of the larger solid is 192.
When two similar solids have a scale factor of 3:4, the volume of the larger solid can be found by cubing the scale factor and multiplying it by the volume of the smaller solid. In this case, if the volume of the smaller solid is 54, the volume of the larger solid is 192.
To know more about volume, visit;
https://brainly.com/question/23705404
#SPJ11
What is the measure of the central angle of a circle with radius 15 ft that intercepts a 10 ft arc?
Use 3.14 for TT.
Round the answer to the hundredths place
Answers
another...https://brainly.com/question/29228806?answering=true&answeringSource=feedPublic%2FhomePage%2F1
Find the value of x.
(2x + 3)
100°
199

Answers
Help with slope pleaseee
^^

Answers
You have to do to get the answer
use green's theorem to find the counterclockwise circulation and outward flux for the field f=(7x−4y)i (9y−4x)j and curve c: the square bounded by x=0, x=4, y=0, y=4.
Answers
The counterclockwise circulation around c is 12 and the outward flux through c is zero.
Green's theorem is a useful tool for calculating the circulation and flux of a vector field around a closed curve in two-dimensional space.
In this case,
we have a field f=(7x−4y)i+(9y−4x)j and
a square curve c bounded by x=0, x=4, y=0, y=4.
To find the counterclockwise circulation, we can use the line integral of f along c, which is equal to the double integral of the curl of f over the region enclosed by c.
The curl of f is given by (0,0,3), so the line integral evaluates to 12.
To find the outward flux, we can use the double integral of the divergence of f over the same region, which is equal to zero since the divergence of f is also zero.
To learn more about : circulation
https://brainly.com/question/30619471
#SPJ11
The height of the probability density function f(x) of the uniform distribution defined on the interval [a, b] is 1/(a-b). True False
Answers
The statement "The height of the probability density function f(x) of the uniform distribution defined on the interval [a, b] is 1/(a-b)" is False.
In a uniform distribution, the probability density function (PDF) is constant within the interval [a, b]. The height of the PDF represents the density of the probability distribution at any given point within the interval. Since the PDF is constant, the height remains the same throughout the interval.
To determine the height of the PDF, we need to consider the interval length. In a uniform distribution defined on the interval [a, b], the height of the PDF is 1/(b - a) for the PDF to integrate to 1 over the entire interval. This means that the total area under the PDF curve is equal to 1, representing the total probability within the interval [a, b].
Therefore, the correct statement is that the height of the probability density function f(x) of the uniform distribution defined on the interval [a, b] is not 1/(a - b), but rather it is a constant value necessary for the PDF to integrate to 1 over the interval, i.e., 1/(b - a).
Learn more about uniform distribution here:
https://brainly.com/question/32291215
#SPJ11
laura graphed the function below y = 1 / 2(One over two)x + 4
if the range of the function is restricted to 2 ≤ y ≤ 6, what is the domain?

Answers
Step-by-step explanation:
y = 0.5x + 4
When y = 2, x = -4. (shown in graph)
When y = 6, x = 4. (shown in graph)
Hence the domain would be -4 <= x <= 4.
A normal population has a mean μ = 35 and standard deviation σ=7 What proportion of the population is less than 45?
Answers
About 92.36% of the population is less than 45 in a normal population with a mean of 35 and a standard deviation of 7.
To find the proportion of the population with a mean (µ) of 35 and a standard deviation (σ) of 7 that is less than 45, follow these steps:
1. Convert the raw score (45) to a z-score using the z-score formula:
z = (X - µ) / σ
where X is the raw score (45), µ is the mean (35), and σ is the standard deviation (7).
2. Calculate the z-score:
z = (45 - 35) / 7
z ≈ 1.43
3. Use a z-table or calculator to find the proportion of the population corresponding to a z-score of 1.43. The z-table or calculator will provide the area under the curve to the left of the z-score, which represents the proportion of the population that is less than the raw score of 45.
4. The z-table or calculator shows a proportion of approximately 0.9236 for a z-score of 1.43.
Learn more about mean:
https://brainly.com/question/1136789
#SPJ11
Subtract: What is 20 - (-3) ?
Answers
Answer: 23
Step-by-step explanation: a P e X
Keeping the properties of exponents in mind, to what power must you raise the expression 7 to get 7 as the result?
Answers
melinda owns a bakery she recently promised her best employee rainbow a raise.she said it would be reflected on rainbows next paycheck when rainbow was paid she instantly looked to see how much of a raise she received she used to make $10.40 per hour for this pay period though she earned $952 for working 80 hours
Answers
Answer: $11.90 per hour
Step-by-step explanation: I got this answer by dividing 952 dollars by 80 hours which resulted in $11.90 per hour.
Henry opens a savings account that has a 4.5% annual interest
rate. After 18 months, he receives $75,000. How much did he invest?
Show all work
Answers
Henry opens a savings account with an annual interest rate of 4.5 percent. After a year, he gets $75,000 in payment. He made a deposit into the savings account of $72,831.68.
Here are the steps on how to calculate the amount Henry invested:
Convert the annual interest rate to a monthly rate.
\(\begin{equation}4.5\% \div 12 = 0.375\%\end{equation}\)
Calculate the number of years.
\(\begin{equation}\frac{18 \text{ months}}{12 \text{ months/year}} = 1.5 \text{ years}\end{equation}\)
Use the compound interest formula to calculate the amount Henry invested.
\(\begin{equation}FV = PV * (1 + r)^t\end{equation}\)
where:
FV is the future value ($75,000)
PV is the present value (unknown)
r is the interest rate (0.375%)
t is the number of years (1.5 years)
\(\begin{equation}\$75,000 = PV \cdot (1 + 0.00375)^{1.5}\end{equation}\)
\$75,000 = PV * 1.0297
\(\begin{equation}PV = \frac{\$75,000}{1.0297}\end{equation}\)
PV = \$72,831.68
Therefore, Henry invested \$72,831.68 in the savings account.
To know more about the annual interest rate refer here :
https://brainly.com/question/20631001#
#SPJ11
what is the solution to this equation?
\( \sqrt[5]{27(x - 2) = 3?} \)
Answers
Answer:
x = 11
Step-by-step explanation:
27x - 54 = 243
x = 11
The measure of angle a and the sum of angle c and b

Answers
Answer:
Part 1: 61 degrees Part 2: 90 degrees
Step-by-step explanation:
m<a = 180 - m<b - m<c - 29
m<c = 29
m<b = 90-29
m<b = 61
m<a = 180 - 61 -29 -29
m<a = 61 degrees
m<c + m<b = 29 + 61
m<c + m<b 90 degrees
A fair 6-sided die is rolled 300 times. What is a reasonable prediction for the number of times the event of landing on an odd number will occur?
A. 150
B. 50
C. 175
D. 100
Answers
Answer:
A. 150
Step-by-step explanation:
Calculate the probability of landing on an odd number: 1/2.
Multiply the probability by the number of trials: (1/2) * 300.
Simplify the expression: 150.
Therefore, a reasonable prediction is that the event of landing on an odd number will occur 150 times out of the 300 rolls of the fair 6-sided die.
Superior segway tours gives sightseeing tours around chicago, illinois. it charges a one-time fee of $60, plus $28 per hour. what is the slope of this situation? a. 28 b. 32 c. 60d. 88
Answers
Answer:
the answer is (a) 28.
Step-by-step explanation:
The given situation can be represented by a linear equation of the form:
Cost = mx + b
where "m" is the slope (the rate of change of cost with respect to time), "x" is the number of hours of the tour, and "b" is the y-intercept (the cost when x = 0).
In this case, the y-intercept is $60, which represents the one-time fee. The cost increases by $28 per hour, so the slope is:
m = $28/hour
Therefore, the answer is (a) 28.
Which statement about equations and expressions is true?
An example of an equation is StartFraction z Over 365 EndFraction because it shows that two expressions are equal.
An example of an expression is StartFraction z Over 365 EndFraction because it shows that two equations are equal.
An example of an equation is StartFraction z Over 365 EndFraction because it is a mathematical phrase represented by numbers, a variable, and an operation.
An example of an expression is StartFraction z Over 365 EndFraction because it is a mathematical phrase represented by numbers, a variable, and an operation.
Answers
Answer:
its d
Step-by-step explanation:
the other person made me get it wrong and i checked and it was d
Answer:
D
Step-by-step explanation:
T equals, 15 n, plus 12, which consists of both a per-ticket charge and a one-time ... Since n represents the number of tickets that Salim purchases, it follows that 15 n ... The two numerical expressions in the given equation can be simplified as ... 4 x squared, plus 6 x, and denominator 4 x plus 2, end fraction is equivalent to.
Match each counting problem on the left with its answer on the right. Instructions The number of ways to pick a digit, a lowercase letter, an uppercase letter, or one of eight allowable punctuation marks The number of ways to pick an integer that is between 1 and 50 (inclusive), 100 and 150 (inclusive), or 200 and 250 (inclusive) The number of ways to pick a county in Illinois, Michigan, Minnesota, or Wisconsin if there are 102 counties in Illinois, 83 in Michigan, 87 in Minnesota, and 72 in Wisconsin The number of departments in a university if there are 38 in Literature, Science, and Arts, 13 in Engineering, 17 in Agriculture, and 8 in the Business School 76 344 70 152
Answers
The number of ways
To pick a digit, a lowercase letter, an uppercase letter, or one of eight allowable punctuation marks is 70 ways. To pick an integer that is between 1 and 50 (inclusive), 100 and 150 (inclusive), or 200 and 250 (inclusive) is 150 ways. To pick a county in Illinois, Michigan, Minnesota, or Wisconsin if there are 102 counties in Illinois, 83 in Michigan, 87 in Minnesota, and 72 in Wisconsin is 344 ways.The number of departments in a university if there are 38 in Literature, Science, and Arts, 13 in Engineering, 17 in Agriculture, and 8 in the Business School 76 departments
1. The number of ways to pick a digit, a lowercase letter, an uppercase letter, or one of eight allowable punctuation marks:
There are 10 digits (0-9), 26 lowercase letters, 26 uppercase letters, and 8 punctuation marks. So the total number of ways is 10 + 26 + 26 + 8 = 70 ways.
2. The number of ways to pick an integer that is between 1 and 50 (inclusive), 100 and 150 (inclusive), or 200 and 250 (inclusive):
There are 50 integers in each range (1-50, 100-150, 200-250). So the total number of ways is 50 + 50 + 50 = 150 ways.
3. The number of ways to pick a county in Illinois, Michigan, Minnesota, or Wisconsin if there are 102 counties in Illinois, 83 in Michigan, 87 in Minnesota, and 72 in Wisconsin:
Total number of ways is the sum of the counties in each state: 102 + 83 + 87 + 72 = 344 ways.
4. The number of departments in a university if there are 38 in Literature, Science, and Arts, 13 in Engineering, 17 in Agriculture, and 8 in the Business School:
Total number of departments is the sum of departments in each school: 38 + 13 + 17 + 8 = 76 departments.
So the final matches are:
- Counting problem 1: 70
- Counting problem 2: 150
- Counting problem 3: 344
- Counting problem 4: 76
For more such questions on Ways.
https://brainly.com/question/29110744#
#SPJ11
how to turn 9/15 into a decimal
Answers
Answer:
Answer 0.6
Step-by-step explanation:
To turn a fraction into a decimal is divide the top from the bottom. 9/15 = 9 ÷ 15 = 0.6 Really, that's all there is to it
how to find the polynmial closest to another polynomial in an inner product space
Answers
To find the polynomial closest to another polynomial in an inner product space, you can follow these steps:
Choose an inner product on the space of polynomials. One common inner product on this space is the L2 inner product, which is defined as:
<f,g> = ∫a^b f(x)g(x) dx,
where a and b are the endpoints of the interval on which the polynomials are defined.
Let P be the space of polynomials of degree at most n, where n is the degree of the polynomial you want to approximate. Let f be the polynomial you want to approximate, and let g be an arbitrary polynomial in P.
Define the error between f and g as e = f - g.
Compute the inner product of e with itself:
<e,e> = ∫\(a^b (f(x) - g(x))^2 dx.\)
Minimize this inner product with respect to g. This can be done by setting the derivative of <e,e> with respect to g equal to zero and solving for g.
The polynomial that minimizes the error is the polynomial closest to f in the L2 sense.
Learn more about polynomial
https://brainly.com/question/11536910
#SPJ4
double u, then divide 6 by the result
Answers
Answer:
wat 12?
Step-by-step explanation:
Answer:
wat 12????????????????????????
What is the cost to rent each chair and each table?
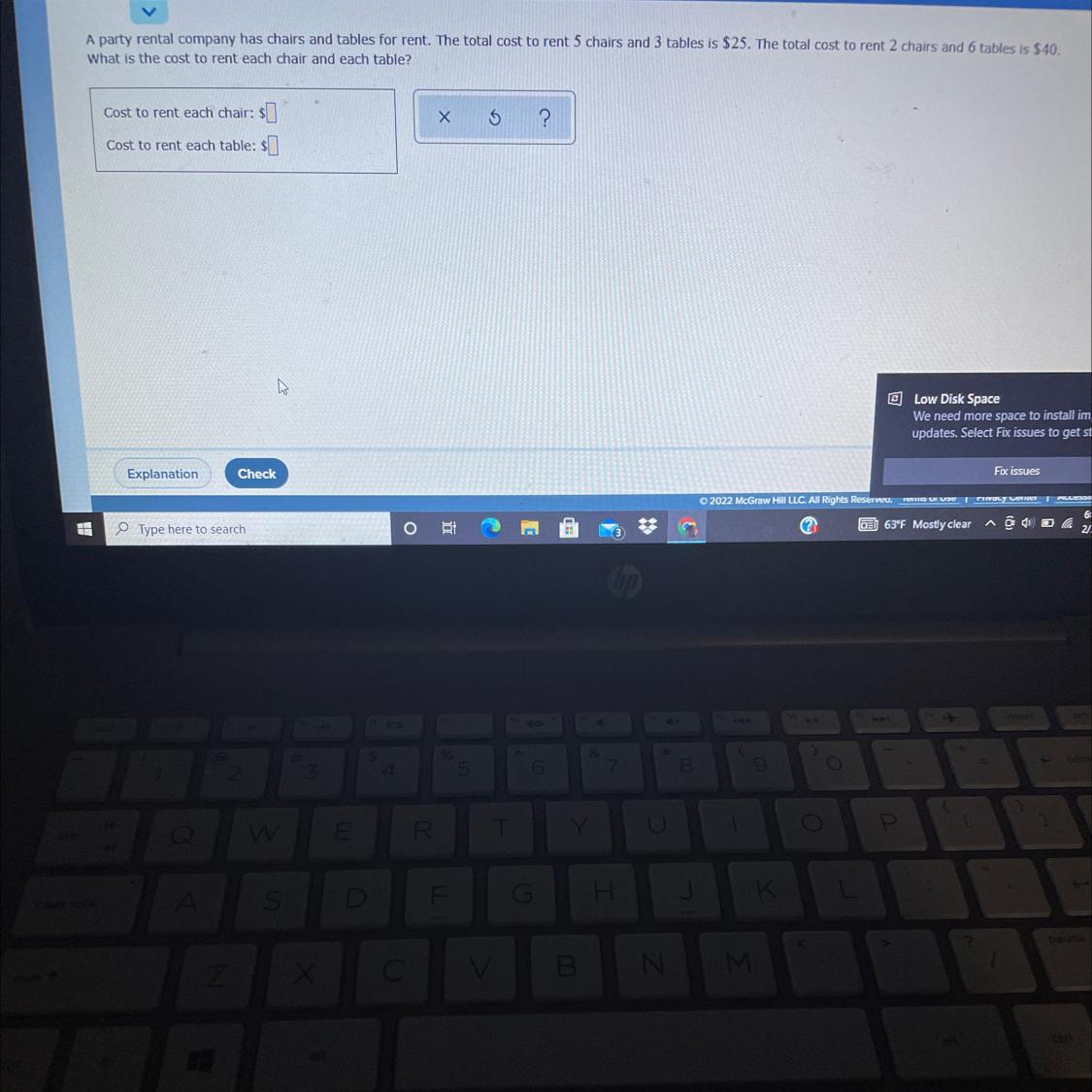
Answers
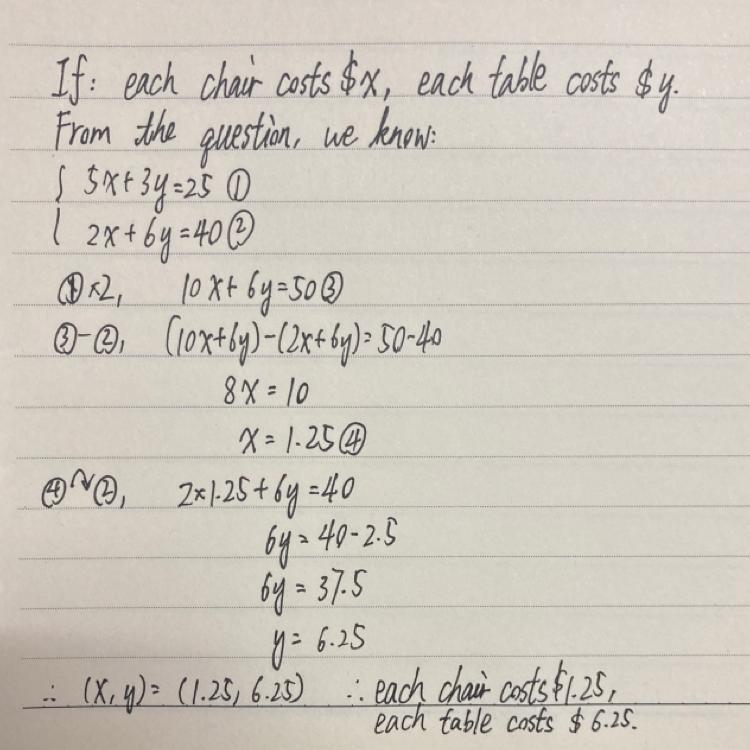
Let μ and σ
2
denote the mean and variance of the random variable X. Determine E[(X−μ)/σ] and E{[(X−μ)/σ]
2
}.
Answers
The expected value of \(\left(\frac{{X - \mu}}{\sigma}\right)^2\) is 1.
The expected value of \((X - \mu)/\sigma\) is 0, and the expected value of \(\left(\frac{{X - \mu}}{\sigma}\right)^2\) is 1.
To find the expected value of \((X - \mu)/\sigma\), we substitute the given formula into the expectation operator:
\(E\left[\frac{{X - \mu}}{\sigma}\right] = \frac{1}{\sigma}E[X - \mu]\)
By linearity of expectation, we can split this expression into:
\(\frac{1}{\sigma}(E[X] - E[\mu])\)
Since \(\mu\) is a constant, its expected value is itself, so \(E[\mu] = \mu\). Substituting \(E[X] = \mu\), we get:
\(\frac{1}{\sigma}(\mu - \mu) = 0\)
Therefore, the expected value of \((X - \mu)/\sigma\) is 0.
Now, let's calculate the expected value of \(\left(\frac{{X - \mu}}{\sigma}\right)^2\):
\(E\left[\left(\frac{{X - \mu}}{\sigma}\right)^2\right] = \frac{1}{\sigma^2}E[(X - \mu)^2]\)
Using the definition of variance, we know that \(E[(X - \mu)^2] = \sigma^2\). Substituting this, we get:
\(\frac{1}{\sigma^2} \cdot \sigma^2 = 1\)
Hence, the expected value of \(\left(\frac{{X - \mu}}{\sigma}\right)^2\) is 1.
Learn more about expectation operator here:
brainly.com/question/33494844
#SPJ11
41. The Puuur Place builds customized cat trees for pet owners. The basic tree is $100 and each additional platform, perch, or toy costs $50. Meow Now also builds customized cat trees. Their basic cat tree starts at $50 and each additional piece costs $75.
[A] Write and solve a system of equations to represent the total cost, y, when x additional pieces are purchased with a basic cat tree at each store.
[B] Solve this system of equations and show your work.
[C] Reggie wants to purchase a cat tree for his pets. Based on your work, explain which store would be cheaper depending on how many add-ons he wants to purchase.
Answers
The system of equations to represent the total cost, y, when x additional pieces are purchased with a basic cat tree at each store are;
y = 50x + 100 ------(eq 1)
y = 75x + 50 ------(eq 2)
How to Solve Simultaneous Equations?A) Let the total cost of the cat tree be y
Let each additional piece added be x.
Since basic tree is $100 and each additional platform costs $50, then we can say that;
y = 50x + 100 ------(eq 1)
Now, their basic cat tree starts at $50 and each additional piece costs $75. Thus;
y = 75x + 50 ------(eq 2)
B) Subtract eq 1 from eq 2 to gte;
25x - 50 = 0
25x = 50
x = 50/25
x = 2
y = 75(2) - 50
y = $100
C) The Store that would be cheaper depending on the add - ons is Puuur Place because as x increases, it's y-value increases at a lesser rate than that of Meow.
Read more about Simultaneous Equations at; https://brainly.com/question/148035
#SPJ1
Clark finds that in an average month, he spends $35 on things he really doesn't need and can't afford. About how much does he spend on these items in a year? I came up with $420?
Answers
Clark spends $ 12775 on these items which he does not need in a year (if we consider 365 days) where the average spend in a month is $35.
Clark finds that in an average month, he spends $35 on things he really doesn't need and can't afford.
Let us consider the month in consideration here to be of 30- days and ignore any months other number of days.
Thus, calculating the average, say x' , by formula, we get,
x' = (Summation of values of all observations ) / ( Number of observations)
⇒ 35 = Total spend / 30
⇒ Total spend = $ ( 35*30)
⇒ Total spend = $ 1050
Therefore, total spend on a year, that is 12 months (considering all months to be of 30- days ) = $( 1050*12) = $ 12600
But we know a year does not have 360 days. So we calculate the total spend on these 5 days where average month spend is $35 is $175.
Hence the total spend for a year with 365 days is = $( 12600 + 175 ) = $12775
To know more about average here
https://brainly.com/question/29895356
#SPJ1
Find the domain of the function h(x) = sin x/ 1- cos x
Answers
To find the domain of the function h(x) = sin(x) / (1 - cos(x)), we need to consider the values of x that make the function well-defined. The domain of a function is the set of all possible input values for which the function produces a valid output.
In interval notation, the domain can be written as:
(-∞, 2π) ∪ (2π, 4π) ∪ (4π, 6π) ∪ ...
In this case, we have two conditions to consider:
1. The denominator, 1 - cos(x), should not be equal to zero. Division by zero is undefined. Therefore, we need to exclude the values of x for which cos(x) = 1.
cos(x) = 1 when x is an integer multiple of 2π (i.e., x = 2πn, where n is an integer). At these values, the denominator becomes zero, and the function is not defined.
2. The sine function, sin(x), is defined for all real numbers. Therefore, there are no additional restrictions based on the numerator.
Combining these conditions, we find that the domain of the function h(x) is all real numbers except those of the form x = 2πn, where n is an integer.
To know more about domains of functions, click here: brainly.com/question/28599653
#SPJ11
The base of an isosceles triangle is 24 cm and its area is 192 cm^2 . Find its perimeter.
Answers
Step-by-step explanation:
Area of Traingle=1/2×b×h
192cm²=1/2×24×h
192cm²=12×h
h=192/12
h=16cm
Hypotenuse ²=Base²+Altitude ²
Hypotenuse ²=12²+16²
Hypotenuse ²=144+256
Hypotenuse ²=400
Hypotenuse =20cm
Perimeter=20+20+24
=64cm
The circumference of a circle is 12π m. What is the area, in square meters? Express your answer in terms of π.
Answers
Answer:
π 36 m^2
Step-by-step explanation:
C = 2π R = 12π m --> R = 6m
A = π R^2 = π 36 m^2
Answer:
Area of circle = 36π m²Step-by-step explanation:
In the question we are given that circumference of circle is 12π m . And we are asked to find the area of circle in term of π .
Solution : -
For finding area of circle we need to find the radius of circle . In the question circumference of circle is given . So we can find radius of circle using it . We know that ,
\( \qquad \quad \pink{\underline{\pink{\boxed{\frak{Circumference_ {(Circle) }= 2\pi r}}}}}\)
Where ,
π refers to 3.14 or 22/7r refers to radius of circleBut as in the question , it is given that we have to find the area in term of π. So we aren't using π as 3.14 or 22/7 .
Now, Radius :
\( \longrightarrow \qquad \: 12 \cancel{\pi }= 2 \cancel{\pi} r\)
Step 1 : Cancelling π and we get :
\( \longrightarrow \qquad \:12 = 2r\)
Step 2 : Dividing both sides by 2 :
\( \longrightarrow \qquad \: \cancel{\dfrac{12}{2} } = \dfrac{ \cancel{2}r}{ \cancel2} \)
On further calculations we get :
\( \longrightarrow \qquad \: \boxed{ \bf{r = 6 \: m}}\)
Therefore , radius of circle is 6 m .Finding Area :
As we have find the radius of circle above so we can find its area easily . We know that ,
\( \qquad \: \qquad \pink{\underline{\pink{ \boxed{{\frak{ Area_{(Circle)} = \: \pi r {}^{2} }}}}}}\)
Now substituting value of radius :
\( \longmapsto \: \qquad \quad\pi (6) {}^{2} \)
\( \longmapsto \: \qquad \quad \pi \times \: 6 \times 6\)
\( \longmapsto \: \qquad \quad \pi \times 36\)
We get :
\( \longmapsto \: \qquad \quad \blue{\underline{\blue{\boxed{\frak{ \bf{36 \pi \: m {}^{2} }}}}}}\)
Therefore, area of circle is 36π square metres .#Keep Learning
Find the nth term: 9,17,25,33
Answers
Answer:
9+8(n-1)
Step-by-step explanation:
1) 9
2) 9+8=17
3) 9+8(2)=25
4) 9+8(3)=33
n) 9+8(n-1)