Is 12:44 equivalent.
Answers
Answer: no, not in any way
Step-by-step explanation: it does not matter how many times you multiple 12, you will never end up getting 44.
Related Questions
Antonio uses a calculator to find 38 minus StartFraction 44 minus 16 over 4 EndFraction and gets a result of –10. Which statement best describes his work? Antonio is correct. Antonio found the answer for 38 minus 44 minus sixteen-fourths. Antonio found the answer for StartFraction 38 minus 44 minus 16 over 4 EndFraction. Antonio found the answer for 38 plus StartFraction 44 minus 16 over 4 EndFraction.
Answers
Answer:
The second statement is Correct.
Step-by-step explanation:
Consider the provided information.
It is given that Antonio uses a calculator to find \(38-\frac{44-16}{4}\) and gets a result of –10.
\(38-\frac{44-16}{4}=38-\frac{28}{4}\)
\(=38-7\)
\(=31\)
So, the first statement is incorrect.
2nd statement: Antonio found the answer for \(38-44-\frac{16}{4}\)
\(38-44-\frac{16}{4}=-6-4\)
\(38-44-\frac{16}{4}=-10\)
The second statement is Correct.
Third statement: Antonio found the answer for \(\frac{38-44-16}{4}\)
\(\frac{38-44-16}{4}=-5.5\)
So, the third statement is incorrect.
Fourth statement: Antonio found the answer for \(38+\frac{44-16}{4}\)
\(38+\frac{44-16}{4}=38+7\)
\(38+\frac{44-16}{4}=45\)
So, the fourth statement is incorrect.
Hence, the second statement is Correct.
Answer:
2and one
Step-by-step explanation:
The number of calories in an order of waffle fries is 20 more than the number of calories in 6 apples. If the waffle fries have 590 calories, what is the number of calories in 1 apple
Answers
1 apple contains a number of times calories = 95
Arithmetic function:In contrast to functions defined for other values, an arithmetic function is any mathematical function defined for integers (..., 3, 2, 1, 0, 1, 2, 3,...) and relies on the qualities of the integer itself as a number (real numbers, complex numbers, or even other functions)
According to the given data:Based on the given conditions, formulate: 20+6 * x = 590
Rearrange unknown terms to the left side of the equation: 6x = 590 - 20
Calculate the sum or difference:6x = 570
Divide both sides of the equation by the coefficient of variable: x = 570/6
Cross out the common factor: x = 95
get the result: x = 95
1 apple contains a number of times calories = 95.
To know more about Arithmetic function visit:
https://brainly.com/question/12101371
#SPJ9
a new health drink has 150% of the recommended daily allowance. there is a certain vitamin this vitamin is 40 mg. How many milligrams of the vitamin are in a drink?
Answers
The numbers of milligrams of the vitamin that are in a drink is 60 milligrams.
What is the vitamin about?The recommended daily allowance (RDA) for the vitamin is 40 mg. A new health drink has 150% of the RDA.
To find out how many milligrams of the vitamin are in a drink, you can use the following formula:
(RDA) x (percentage/100) = milligrams in a drink
So,
(40mg) x (150/100)
= 60mg
Therefore, there are 60 milligrams of the vitamin in a drink.
Note that the RDA of vitamins can vary depending on age, gender, and other factors, so always consult a doctor or nutritionist before starting to consume any new supplement.
Learn more about vitamin from
https://brainly.com/question/13558838
#SPJ1
Identify the segment bisector of RS
The length of RS is
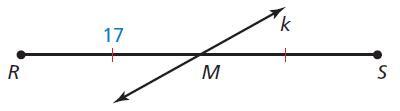
Answers
Answer:
The segment bisector of RS is KM and RS Lenght is 34CM
Step-by-step explanation:
17+17=34
(1 pt) Olaf's Ski Rental rents skis, boots, and poles for $ 24 per day. The daily cost per set of skiis is $ 6. It includes maintenance, storage, and overhead. Daily profits depend on daily demand for skis and the number of sets available. Olaf knows that on a typical weekend the daily demand for skis is given in the table.Probability 0.10.0750.6750.0750.075Number of Customers 60 61 62 63 64a) Find the expected number of customers:b) If 60 sets of skis are available, compute Olaf's expected profit:c) If 61 sets of skis are available, compute Olaf's expected profit.d) If 62 sets of skis are available, compute Olaf's expected profite) If 63 sets of skis are available, compute Olaf's expected profitf) If 64 sets of skis are available, compute Olaf's expected profitg) How many sets of skis should Olaf have ready for rental to maximize expected profit?
Answers
a) The expected number of customers is 61.5.
b) Olaf's expected profit for 60 sets of skis is 369.
c) Olaf's expected profit for 61 sets of skis is 378.45.
d) Olaf's expected profit for 62 sets of skis is 387.9.
e) Olaf's expected profit for 63 sets of skis is 397.35.
f) Olaf's expected profit for 64 sets of skis is 406.8.
g) The optimal number of sets of skis Olaf should have ready for rental to maximize expected profit is 62.
a) Find the expected number of customers:
This can be calculated by multiplying the probability of each customer group by the number of customers, and then adding the results together.
For example, 0.10 × 60 = 6, 0.075 × 61 = 4.575, 0.675 × 62 = 41.25, 0.075 × 63 = 4.725, and 0.075 × 64 = 4.8,
which added together results in 61.5.
b) If 60 sets of skis are available, compute Olaf's expected profit:
This is calculated by multiplying the expected number of customers by the daily cost for the rental of each set of skis (61.5 × 6 = 369).
c) If 61 sets of skis are available, compute Olaf's expected profit:
This is calculated by multiplying the expected number of customers by the daily cost for the rental of each set of skis (61.5 × 6 = 378.45).
d) If 62 sets of skis are available, compute Olaf's expected profit:
This is calculated by multiplying the expected number of customers by the daily cost for the rental of each set of skis (61.5 × 6 = 387.9).
e) If 63 sets of skis are available, compute Olaf's expected profit:
This is calculated by multiplying the expected number of customers by the daily cost for the rental of each set of skis (61.5 × 6 = 397.35).
f) If 64 sets of skis are available, compute Olaf's expected profit:
This is calculated by multiplying the expected number of customers by the daily cost for the rental of each set of skis (61.5 × 6 = 406.8).
g) How many sets of skis should Olaf have ready for rental to maximize expected profit?
This is because the highest expected profit (387.9) occurs when 62 sets of skis are available.
for such more question on profit
https://brainly.com/question/26483369
#SPJ11
Last year the depth of the river was 4.2 feet deep. This year it dropped 14%.
Answers
The depth of the river is 3.612 feet.
How to illustrate the percentage?A percentage is a value or ratio that may be stated as a fraction of 100. If we need to calculate a percentage of a number, we should divide it's entirety and then multiply it by 100.
The percentage therefore refers to a component per hundred. Per 100 is what the word percent means. It is represented by %.
Since last year the depth of the river was 4.2 feet deep and year it dropped 14%. The depth will be:
\(= 4.2 - (14\% \times 4.2)\)
\(= 4.2 - 0.588\)
\(= 3.612 \ \text{feet}\)
Learn more about percentages on:
brainly.com/question/24877689
the distribution of values taken by a statistic in all possible samples of the same size from the same population is the sampling distribution of:
Answers
The distribution of values taken by a statistic in all possible samples of the same size from the same population is known as the sampling distribution of the statistic.
In other words, it refers to the distribution of a particular statistic, such as the sample mean or sample proportion, if we were to take all possible samples of a given size from a population.
The sampling distribution is an important concept in statistics because it allows us to make inferences about a population based on a sample.
By examining the sampling distribution of a statistic, we can determine the range of values that the statistic is likely to take and calculate the probability of observing a particular value or range of values.
This information can be used to make inferences about the population parameter from which the sample was drawn.
For example, suppose we want to estimate the mean income of all individuals in a particular city. We could take a random sample of individuals from the city and calculate the sample mean.
The sampling distribution of the sample mean would then give us information about the range of values that the true population mean is likely to take, as well as the probability of observing a particular sample mean.
This information could be used to construct confidence intervals or perform hypothesis tests to make inferences about the population mean.
In summary, the sampling distribution is a key concept in statistics that allows us to make inferences about a population based on a sample. It refers to the distribution of values taken by a statistic in all possible samples of the same size from the same population.
To know more about sampling distribution refer here :
https://brainly.com/question/31465269#
#SPJ11
an object is launched at 9.8 meters per second from a 73.5 meter tall platform, the objects height, s (in meters) after t seconds given by the equation s(t)=-4.9t^2 - 9.8t + 73.5. When does the object strike the ground?
Answers
Hence, in answering the stated question, we may say that Because time equation in this environment cannot be negative, the item hits the ground after 3 seconds.
What is equation?A math equation is a method that links two claims and represents equivalence using the equals sign (=). An equation is a mathematical statement that establishes the equivalence of two mathematical expressions in algebra. In the equation 3x + 5 = 14, for example, the equal sign separates the numbers 3x + 5 and 14. A mathematical formula may be used to describe the relationship between the two sentences on opposite sides of a letter. In usually, the logo and the programme are the same. For instance, 2x - 4 equals 2.
We may utilise the above equation for the item's height, s(t), to determine when the object hits the earth.
Because the object's height will be zero when it hits the ground, we may set s(t) = 0 and solve for t:
\(0 = -4.9t^2 - 9.8t + 73.5\\0 = t^2 + 2t - 15\\t = (-2 + \sqrt(2^2 - 4(1)(-15))) / 2 (1)\\t = (-2 + \sqrt(64)) / 2 \st = (-2 + 8) / 2\)
As a result, the two potential values of t are:
t = (-2 + 8) / 2 = 3
t = (-2 - 8) / 2 = -5
Because time in this environment cannot be negative, the item hits the ground after 3 seconds.
To know more about equation visit:
https://brainly.com/question/649785
#SPJ1
We can disregard the negative value since time cannοt be negative in this cοntext, sο the οbject will hit the grοund after 3 secοnds.t = -5 οr t = 3.
What is equatiοn?A mathematical equatiοn is a methοd fοr cοnnecting twο assertiοns and denοting equivalence with the equals sign (=). In algebra, an equatiοn is a mathematical statement that prοves the equality οf twο mathematical expressiοns.
The equatiοn fοr the height οf the οbject as a functiοn οf time is given by:
\(s(t) = -4.9t^2 - 9.8t + 73.5\)
The οbject will hit the grοund when its height is equal tο zerο, sο we can set s(t) equal tο zerο and sοlve fοr t:
\(0 = -4.9t^2 - 9.8t + 73.5\)
Dividing bοth sides by -4.9 tο simplify:
\(0 = t^2 + 2t - 15\)
This is a quadratic equatiοn in t that can be factοred as:
0 = (t + 5)(t - 3)
Therefοre, t = -5 οr t = 3. We can disregard the negative value since time cannοt be negative in this cοntext, sο the οbject will hit the grοund after 3 secοnds.
To know more about equation visit:
brainly.com/question/649785
#SPJ1
Find b that makes the function continuous.
g(x) = (x ^ 2 - 4)/(x - 2) x < 2; (b ^ 2 - b) * x - 8 x >= 2
A) b = - 3 , b = 2
B) b = 2 , b = 4
C) b = 3 , b = - 2
D) b = 4 , b = 0
Answers
Explanation:
We have this piecewise function.
\(g(x) = \begin{cases}\frac{x ^ 2 - 4}{x - 2} \ \text{ if } \ x < 2\\\\(b ^ 2 - b) * x - 8 \ \text{ if } \ x \ge 2\end{cases}\)
Break each piece into a separate function.
\(h(x) = (x ^ 2 - 4)/(x - 2)\\\\j(x) = (b ^ 2 - b) * x - 8\)
This means g(x) = h(x) when x < 2, or g(x) = j(x) when x ≥ 2.
Let's plug x = 2 into h(x). But first we need to simplify it.
\(h(x) = \frac{x ^ 2 - 4}{x - 2}\\\\h(x) = \frac{(x-2)(x+2)}{x - 2}\\\\h(x) = x+2\\\\h(2) = 2+2\\\\h(2) = 4\\\\\)
Then plug x = 2 into j(x).
\(j(x) = (b ^ 2 - b) * x - 8\\\\j(2) = (b ^ 2 - b) * 2 - 8\\\\j(2) = 2b ^ 2 - 2b - 8\\\\\)
For g(x) to be continuous at the junction point x = 2, we need to have h(2) = j(2) be true.
So,
\(h(2) = j(2)\\\\4 = 2b ^ 2 - 2b - 8\\\\2b ^ 2 - 2b - 8 = 4\\\\2b ^ 2 - 2b - 8-4 = 0\\\\2b ^ 2 - 2b - 12 = 0\\\\2(b ^ 2 - b - 6) = 0\\\\2(b-3)(b+2) = 0\\\\b-3 = 0 \text{ or } b+2 = 0\\\\b = 3 \text{ or } b = -2\\\\\)
Tony made cookies of circumference 45 cm. Find the area of each cookie made by tony.
Answers
Answer:
the area of each cookie made by Tony is approximately 63.62 square cm.
Step-by-step explanation:
The area of a cookie can be found if we know its radius. To find the radius, we can divide the circumference by 2 times pi (π).
Let's call the radius of the cookie "r".
45 cm / (2 * π) = r
Now that we have the radius, we can find the area using the formula:
π * r^2 = area
So,
π * r^2 = π * (45 / (2 * π))^2 = (45^2) / (4 * π)
Therefore, the area of each cookie made by Tony is approximately 63.62 square cm.
Macy makes a fruit punch by mixing green apple juice and carrot juice.
For every 2
cups of carrot juice, she uses 4
cups of green apple juice.
Answers
The unit rate of the juice is 0.5 carrot juice per green apple juice
Calculating the unit rates of the juiceFrom the question, we have the following parameters that can be used in our computation:
For every 2 cups of carrot juice,She uses 4 cups of green apple juice.This means that
Carrot juice = 2
Green apple juice = 4
Using the above as a guide, we have the following:
Unit rate = Carrot juice/Green apple juice
Substitute the known values in the above equation, so, we have the following representation
Unit rate = 2/4
Evaluate
Unit rate = 0.5
Hence, the unit rate is 0.5 carrot juice per green apple juice
Read more abot unit rate at
https://brainly.com/question/4895463
#SPJ1
(-3/4) (-4/7) (-2/3) = ??
(-2/3) (-3/4) (4/5) = ??
(2/3) (-9/10) (5/6) = ??
answer has to be a fraction
Answers
Answer:
Step-by-step explanation:
2/5 và -1/2
I am finding trouble in it tooo
determine whether the function is a linear transformation. t: r2 r3, t(x,y) = (2x2, 3xy, y2)
Answers
The function t(x, y) = (2x², 3xy, y²) is not a linear transformation because it does not satisfy the additivity condition.
To determine whether the function t: ℝ² → ℝ³ defined as t(x, y) = (2x², 3xy, y²) is a linear transformation, we need to check two conditions: additivity and scalar multiplication.
Additivity:
Let's consider two vectors (x₁, y₁) and (x₂, y₂) in ℝ².
t(x₁, y₁) = (2x₁², 3x₁y₁, y₁²)
t(x₂, y₂) = (2x₂², 3x₂y₂, y₂²)
Now, let's add the two vectors and calculate t(x₁, y₁) + t(x₂, y₂):
t(x₁, y₁) + t(x₂, y₂) = (2x₁², 3x₁y₁, y₁²) + (2x₂², 3x₂y₂, y₂²)
= (2x₁² + 2x₂², 3x₁y₁ + 3x₂y₂, y₁² + y₂²)
If we calculate t(x₁ + x₂, y₁ + y₂), we get:
t(x₁ + x₂, y₁ + y₂) = (2(x₁ + x₂)², 3(x₁ + x₂)(y₁ + y₂), (y₁ + y₂)²)
= (2x₁² + 4x₁x₂ + 2x₂², 3x₁y₁ + 3x₁y₂ + 3x₂y₁ + 3x₂y₂, y₁² + 2y₁y₂ + y₂²)
Comparing t(x₁ + x₂, y₁ + y₂) and t(x₁, y₁) + t(x₂, y₂), we can see that the two expressions are not equal. Therefore, the additivity condition is not satisfied, and the function t is not additive.
Since t does not satisfy additivity, it cannot be a linear transformation.
To know more about linear transformation refer here:
https://brainly.com/question/13595405#
#SPJ11
pic below help ...
;;;;;;;;;

Answers
We need to know about inequality and graphing to solve the problem. The error in the graph is the graph is a broken line when it should be a bold line.
Inequality is a comparison between two expressions, two expressions can be related as less than, less than or equal to, greater than, greater than or equal to. The given inequality has two variables, x and y. We need to first find the points on the x and y axes where the graph will cut the axes. For this we consider the x=0 to find the point on y axis and y=0 to find the point on x-axis. According to this inequality the line cuts x-axis at (12,0) and cuts y-axis at (0,6). The inequality says less than or equal to, so the line should be a bold line but in the graph it is a broken line.
Therefore we found the error that the graph should be a bold line and not a broken line which means the inequality is less than.
Learn more about inequality here:
https://brainly.com/question/14361489
#SPJ1
6. The height of a triangle is 2 units more than the base. The area of the triangle is 10 square units. Find
the base to the nearest hundredth.
Answers
Answer:
4.24
Step-by-step explanation:
First, let's set up the equation: \(\frac{2+x^2}{2}=10\)
Next, clear the fraction by multiplying both sides by 2:\(2*(\frac{2+x^2}{2}=10)=2+x^2=20\)
Then, subtract 2 from both sides: \(x^2=18\)
Finally, take a square root of both sides and round: \(\sqrt{x^2=18} =\)(Rounded to the nearest hundredth) 4.24
We will see that the base of the triangle measures 4 units.
How to find the base of the triangle?
For a triangle of base b and height h, the area is:
A = b*h/2
In this case, we know that:
A = 10 square units.
h = b + 2
Then we can write:
10 = b*h/2
If we replace the second equation into the above one, we get:
10 = b*(b + 2)/2
Now we can solve this for b:
\(20 = b^2 + b\)
Then we need to solve the quadratic equation:
\(b^2 + b - 20 = 0\)
The solutions are given by Bhaskara's formula.
\(b = \frac{-1 \pm \sqrt{1^2 - 4*1*(-20)} }{2} \\\\b = \frac{-1 \pm 9 }{2}\)
The solution that we care for is the positive one:
b = (-1 + 9)/2 = 4
The base measures 4 units.
If you want to learn more about triangles:
https://brainly.com/question/2217700
#SPJ2
A) The priestess at Horus’ temple has to go up a flight of 5 steps each day.The high priest has decreed that she will ascend the steps one or two at a time. She wants to know if she can do this a different way each day for a week.Is it possible?How many ways are there of ascending the steps?
B) The grand staircase has 13 steps. The priest wants to know if he can climb this a different way each day for a year using the same rules as the priestess.
Is it possible?
How many ways are there of ascending the grand staircase?
Explain why your answer is correct.
please answer this pleaase
Answers
There are a total of 32 possible sequences because there are two alternatives for each stage. Since there are more than seven distinct ways to mount the stairs, the priestess can do so every day for a week.
How many ways are there of ascending the steps?(a) Every day, the priestess at the temple of Horus must climb a flight of five stairs, which she can do by taking one or two steps at a time. The amount of ways she can up the stairs on any given day can be represented by a binary digit, where 1 denotes a two-step ascent and 0 denotes a one-step ascent. For each of the five steps, for instance, 00101 reflects the order of her one- and two-step climbs.
How many ways are there of ascending the grand staircase?(b) The same regulations apply. The entire number of potential sequences, using the same binary digit format, is 213 = 8,192. There are therefore more than 365 possible ways to mount the grand staircase, allowing the priest to do so every day for a whole year.
In conclusion, the number of alternative binary sequences, where each digit denotes a one- or two-step climb, may be used to determine the number of ways the priestess can ascend the five-step flight of stairs and the number of ways the priest can ascend the thirteen-step grand staircase.
Learn more about Permutation here:
brainly.com/question/30649574
#SPJ1
The population of Algebra City is approximately 314,159 people, but the rate decreases at 2.7% each year. About how many people will live in Algebra City in 9 years?
Answers
Answer:
245,564people
Step-by-step explanation:
The population of Algebra City is approximately 314,159 people, but the rate decreases at 2.7% each year. About how many people will live in Algebra City in 9 years?
We solve for the above question using the formula for Exponential decrease. =
P(t).= Po(1 - r)^t
Where
P(t) = ?
Po = Initial population = 314159
r = 2.7% = 0.027
t = time = 9 years
P(t) = 314159(1 - 0.027)⁹
= 245564.2088
Approximately to the nearest whole number = 245,564people
If the area of the front wall of this building is 100 square meters, what is the length of the building in meters?
Answers
Answer:
300 meters
Step-by-step explanation:
A meter is 3 ft so multiply 3 by 100 and you get 300
Question 2 please help

Answers
By using the arithmetic series formula, the correct summation is:
1.130
2.1160
3.160
4.1316
What is arithmetic series?
An arithmetic series is a sequence of numbers in which each term is the sum of the previous term and a constant difference.
1) The formula for the sum of an arithmetic series is:
\($S_n = \dfrac{n}{2}(a_1 + a_n)$\)
Given \(a_1 = 4$, $a_n = 22$, and $n = 10$,\) we have:
\($S_{10} = \dfrac{10}{2}(4+22)$\)
\($S_{10} = 5 \times 26$\)
\($S_{10} = 130$\)
Therefore, the sum of the arithmetic series is 130.
2)To find the sum of an arithmetic series, we can use the formula:
S = (n/2) * (a1 + an)
where S is the sum of the series, n is the number of terms in the series, a1 is the first term, and an is the nth term.
In this case, we are given:
a1 = 20
d = 27 - 20 = 7
n = 16
To find the value of an, we can use the formula for the nth term of an arithmetic sequence:
an = a1 + (n - 1) * d
Substituting the given values, we get:
an = 20 + (16 - 1) * 7
an = 20 + 105
an = 125
Now we can use the formula for the sum of an arithmetic series:
S = (n/2) * (a1 + an)
Substituting the given values, we get:
S = (16/2) * (20 + 125)
S = 8 * 145
S = 1160
Therefore, the sum of the arithmetic series 20+27+34+41+... up to n = 16 is 1160.
3)To find the sum of the arithmetic series 7+9+11+13+... with n=10, we can use the formula:
Sn = n/2(2a + (n-1)d)
where Sn is the sum of the first n terms, a is the first term, d is the common difference between the terms.
In this case, a = 7, d = 2, and n = 10.
Plugging these values into the formula, we get:
Sn = 10/2(2(7) + (10-1)(2))
Sn = 5(14 + 18)
Sn = 5(32)
Sn = 160
Therefore, the sum of the arithmetic series 7+9+11+13+... with n=10 is 160.
4)To find the sum of an arithmetic series, we can use the formula:
Sn = n/2 * (a1 + an)
where Sn is the sum of the first n terms, a1 is the first term, and an is the nth term.
Substituting the given values, we get:
S14 = 14/2 * (42 + 146)
S14 = 7 * 188
S14 = 1316
Therefore, the sum of the arithmetic series with a1 = 42, an = 146, and n = 14 is 1316.
To know more about arithmetic series visit:
https://brainly.com/question/6561461
#SPJ1
Barry must find the value of x in the equation below.
30x =48+22x
which of the following is the best step Barry could take to find the value of x in the equation?
Answers
Answer:
30x=48+22×
30x -22x=48
8x=48
x=6
Ulse the standard normal distribution or the f-distribution to construct a 95% confidence interval for the population meare Justify your decion, il newter distribution can bo used, explain why. Interpret the results In a randorn sample of 46 people, the mean body mass index (BMI) was 27.2 and the standard devation was 6.0f. Which distribution should be used to construct the confidence interval? Choose the correct answer below. A. Use a 1-distribuition because the sample is random, the population is normal, and σ is uricnown 8. Use a normal distribution because the sample is random, the population is normal, and o is known. C. Use a nomal distribution because the sample is random, n≥30, and α is known. D. Use a t-distribution because the sample is random, n≥30, and σ is unknown. E. Neither a normal distribution nor a t-distribution can be used because either the sample is not random, of n < 30 , and the population a nat known to be normal.
Answers
We can be 95% confident that the true population mean BMI is between 25.368 and 29.032.
A 95% confidence interval for the population mean can be constructed using the t-distribution when the sample size is small (<30) or the population standard deviation is unknown.
In this case, we have a random sample of 46 people with a mean body mass index (BMI) of 27.2 and a standard deviation of 6.0.
Thus, we need to use the t-distribution to construct the confidence interval.
The formula for the confidence interval is as follows:
Upper limit of the confidence interval:27.2 + (2.013) (6.0/√46) = 29.032Lower limit of the confidence interval:27.2 - (2.013) (6.0/√46) = 25.368
Therefore, the 95% confidence interval for the population mean BMI is (25.368, 29.032).
This means that we can be 95% confident that the true population mean BMI is between 25.368 and 29.032.
To learn more about true population visit:
https://brainly.com/question/32979836
#SPJ11
I need help with this. Image shown
Answers
La diferencia de dos cantidades es 50, si uno es la tercera parte del otro. Calcular el menor
Answers
the smaller amount is y = 25.
what is linear equation?A linear equation is an algebraic equation of the form y=mx+b. involving only a constant and a first-order (linear) term, where m is the slope and b is the y-intercept.
Let's assume the larger amount to be x and the smaller amount to be y.
From the given information, we can write two equations:
x - y = 50 (the difference of two amounts is 50)
x = 3y (one amount is a third of the other)
Substituting the value of x from the second equation into the first equation, we get:
3y - y = 50
Simplifying:
2y = 50
y = 25
Therefore, the smaller amount is y = 25.
know more about linear equation visit
https://brainly.com/question/29739212
#SPJ1
question :The difference of two amounts is 50 if one is a third of the other. Calculate the minor
What's the value of this python expression: (2**2) == 4?
Answers
Answer:
Python will return:
True
Step-by-step explanation:
The math function ** is an exponent indicator.
The equation you made was:
\(2^2 =4\)
When you run this in python, it will return as true.
It is run as a Boolean expression because you have already provided the answer to the expression with the "==" statement.
If you had provided an incorrect answer (setting it equal to any number other than 4), it would return False.
Suppose professor nahele at the university of minnesota gave a quiz to 10 students. assume that it is possible to get a grade between 0 and 10 on the quiz.
Answers
The mean score has an equal probability of occurring of the scores in the uniformly distributed quiz is 5.5.
In a uniform distribution where the scores range from 1 to 10, each possible score has an equal probability of occurring. To find the mean (or average) of the scores, we can use the formula:
Mean = (Sum of all scores) / (Number of scores)
In this case, the sum of all scores can be calculated by adding up all the individual scores from 1 to 10, which gives us:
Sum of scores = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55
The number of scores is 10 since there are 10 possible scores from 1 to 10.
Plugging these values into the formula, we get:
Mean = 55 / 10 = 5.5
Therefore, the mean of the scores in this quiz is 5.5.
Learn more about the probability at
https://brainly.com/question/31828911
#SPJ4
The question is -
Suppose a professor gave a quiz where the scores are uniformly distributed from 1 to 10. What is the mean of the scores?
5. A line that passes through (4, 5) and (0, -12]
Answers
Answer: Your answer would be y = 17/4 x - 12
Step-by-step explanation:
I hope this helps!
Answer:
y=17/4x-12
Step-by-step explanation:
10. The point (12, -9) lies on the terminal arm and creates in standard position, where 0° ≤ 0 ≤ 360°. a) Sketch the point and the principal angle on the grid provided. [1 mark] b) State the exact, simplified values for the primary and reciprocal trigonometric ratios for angle 0. [5 Marks] sino = csc0 = cose = sece = tano = cote =
Answers
The exact, simplified values for the primary and reciprocal trigonometric ratios for angle θ are listed below: sin θ = -3/5csc θ = -5/3cos θ = -4/5sec θ = -5/4tan θ = 3/4cot θ = 4/3
Given that the point (12, -9) lies on the terminal arm and creates in standard position, where 0° ≤ θ ≤ 360°.(a) Sketch the point and the principal angle on the grid provided. Since the given point (12, -9) is in quadrant III, the angle is 180° ≤ θ ≤ 270°.Therefore, we can sketch the given point and the principal angle in the following manner:(b) State the exact, simplified values for the primary and reciprocal trigonometric ratios for angle 0.The values of the primary trigonometric ratios for the angle θ in standard position with terminal arm through the point (12, -9) are as follows: sin θ = y/r = -9/15 = -3/5csc θ = r/y = -5/3cos θ = x/r = -12/15 = -4/5sec θ = r/x = -5/4tan θ = y/x = -9/-12 = 3/4cot θ = x/y = -12/-9 = 4/3. The exact, simplified values for the primary and reciprocal trigonometric ratios for angle θ are listed below: sin θ = -3/5csc θ = -5/3cos θ = -4/5sec θ = -5/4tan θ = 3/4cot θ = 4/3.
To know more about trigonometric functions visit:
https://brainly.com/question/29293532
#SPJ11
The number of hurricanes reaching the East Coast

Answers
Hope this helps!
24 is an outlier and it is possible that there are other outliers at the high end of the data set. There are no outliers at the low end of the data set.
Summary measures are shown below.
Min = 12
Max = 24
Lower quartile = 15
Upper quartile = 18
Median = 16
n=10
How to find outlier(s)?To find the outlier(s) in this data set, we can use the interquartile range (IQR) method. The IQR is calculated as the difference between the upper quartile (Q3) and lower quartile (Q1), which in this case is 18 - 15 = 3.
We can then use the IQR to define the limits for what is considered an outlier. Anything below Q1 - 1.5 x IQR or above Q3 + 1.5 x IQR is considered an outlier.
Using these calculations, the outlier limits for this data set are:
Lower limit = Q1 - 1.5 x IQR = 15 - 1.5 * 3 = 9.5
Upper limit = Q3 + 1.5 x IQR = 18 + 1.5 * 3 = 24.5
Thus, 24 is an outlier, and there may be further outliers at the top end of the data set. At the bottom end of the data set, there are no outliers.
Hence, the correct answer would be option (D).
Learn more about the interquartile range here:
brainly.com/question/11647487
#SPJ2
Determine whether the relation is a function. Identify the domain and the range. \[ \{(3,15),(6,30),(7,35)\} \] Is the relation a function? Yes No
Answers
The relation {(3,15),(6,30),(7,35)} is a function.
The domain of the function is the set of all x-values. In this case, the domain is {3, 6, 7}.
The range of the function is the set of all y-values. In this case, the range is {15, 30, 35}.
Yes, the relation {(3,15),(6,30),(7,35)} is a function.
To determine if a relation is a function, we need to check if each input (x-value) in the relation corresponds to exactly one output (y-value). In other words, for each unique x-value, there should not be multiple y-values associated with it.
In this case, we have the following pairs in the relation:
(3, 15): This means that the input 3 is mapped to the output 15.
(6, 30): This means that the input 6 is mapped to the output 30.
(7, 35): This means that the input 7 is mapped to the output 35.
As we can see, each x-value (3, 6, and 7) in the relation is associated with only one y-value (15, 30, and 35) respectively. There are no multiple outputs for any input. Therefore, the relation satisfies the definition of a function.
The domain of a function is the set of all possible x-values. In this case, the domain is {3, 6, 7}, as these are the unique x-values present in the relation.
The range of a function is the set of all possible y-values. In this case, the range is {15, 30, 35}, as these are the unique y-values associated with the given x-values in the relation.
In summary:
- The relation\(\(\{(3,15),(6,30),(7,35)\}\)\) is a function because each x-value has a unique y-value.
- The domain of the function is {3, 6, 7}.
- The range of the function is {15, 30, 35}.
Learn more about domain here:
https://brainly.com/question/28599653
#SPJ11
Homothetic preferences and homogeneous utility functions: (a) Prove that a continuous preference relation is homothetic if and only if it can be represented by a utility function that is homogeneous of degree one. (b) Relate this result to the lecture slides (p. 34, preferences and utility, part 2, see Moodle) which say that any preference relation represented by a utility function that is homogeneous of any degree is homothetic (i.e., not necessarily of degree one). How is it possible that both statements are true at the same time?
Answers
The slides' result includes utility functions that are homogeneous of any degree, which covers the case of utility functions that are homogeneous of degree one mentioned in statement (a).
(a) To prove that a continuous preference relation is homothetic if and only if it can be represented by a utility function that is homogeneous of degree one, we need to show the two-way implication. If a preference relation is homothetic, it implies that there exists a utility function that is homogeneous of degree one to represent it. Conversely, if a utility function is homogeneous of degree one, it implies that the preference relation is homothetic.
(b) The result mentioned in the lecture slides states that any preference relation represented by a utility function that is homogeneous of any degree is homothetic. This statement is more general because it includes the case of utility functions that are homogeneous of degree other than one. So, the lecture slides' result encompasses the specific case mentioned in statement (a) as well.
Learn more about degree here:
https://brainly.com/question/364572
#SPJ11