In a survey, the ratio of students who prefer popcorn to potato chips is 3 to 4. If the number of students surveyed who prefer popcorn is 360, how many preferred potato chips?
Answers
Answer:
480
Step-by-step explanation:
3/4 =360/x
3x=360*4(cross multipication)
3x=1440
x=1440/3
x=480
The students preferring chips=480
The number of students who preferred potato chips are 480.
We have the ratio of students who prefer popcorn to potato chips.
We have to determine how many preferred potato chips.
What is Ratio ?The quantitative relation between two amounts showing the number of times one value contains or is contained within the other.
According to the question -
Ratio of popcorn and potato chips = 3 : 4
Students who preferred popcorn = 360
Assume that the students who preferred potato chips be x.
Then -
\($\frac{3}{4}=\frac{360}{x}\)
x = 120 x 4 = 480
Hence, the number of students who preferred potato chips are 480.
To solve more questions on ratios, visit the link below-
https://brainly.com/question/16176682
#SPJ2
Related Questions
Calculate the circumference of a circle with a radius of 8 inches.
Answers
To calculate the circumference of a circle, you can use the formula:
\(\displaystyle C=2\pi r\)
Where \(\displaystyle C\) represents the circumference and \(\displaystyle r\) represents the radius of the circle.
Given that the radius \(\displaystyle r\) is 8 inches, we can substitute this value into the formula:
\(\displaystyle C=2\pi (8)\)
Simplifying the expression:
\(\displaystyle C=16\pi \)
Thus, the circumference of a circle with a radius of 8 inches is \(\displaystyle 16\pi \) inches.
Note: \(\displaystyle \pi \) represents the mathematical constant pi, which is approximately equal to 3.14159.
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
A quick answer please thank you.Second one: is - is not Third one: greater than, equal to, less than

Answers
Given that:
\(P(exactly\text{ }58\text{ }girls)=0.0223\)\(P(\text{ }58\text{ }or\text{ }more\text{ }girls)=0.067\)You know that in order for the number of girls to be significantly high, the probability must be:
\(P(x)\leq0.05\)In this case, you can determine that 58 girls in 100 births is a significantly high number, because:
\(P(exactly\text{ }58\text{ }girls)=0.0223\)And:
\(0.0223<0.05\)Notice that the probability for exactly 58 girls is less than 0.05.
Hence, the answer is:
The relevant probability is
\(P(exactly\text{ }58\text{ }girls)=0.0223\)so 58 girls in 100 births is a significantly high number because the relevant probability is less than 0.05.
ASAP!!! NEED AN ANSWER
In this budget scenario, use 15 per hour as the current wage for 40 hour work weeks. Hint: There are 52 weeks in a year, and 12 months in a year.
1. What is the gross yearly income?
2. What is the gross monthly income using this pay rate?
Answers
1)Gross Yearly Income = Hourly Wage × Hours per Week × Weeks in a Year
Gross Yearly Income = $15/hour × 40 hours/week × 52 weeks/year
Gross Yearly Income = $31,200
2)Gross Monthly Income = Gross Yearly Income / Months in a Year
Gross Monthly Income = $31,200 / 12 months
Gross Monthly Income ≈ $2,600
Write an exponential equation in the form y = ab* whose graph passes through points (2, 18) and (5, 60.75).
Answers
Let \(y=ab^x,\) as described in the problem statement. Plugging in \(x=2\) and \(x=5\) gives us the equations \(18=ab^2\) and \(60.75=ab^5.\) Since \(a,b\) are nonzero, we divide the second equation by the first to get \(\frac{27}{8}=b^3,\) which means that \(b=\frac{3}{2},\) after taking the cube root. Plugging this value for \(b\) into the first equation, we now have \(18=a(3/2)^2=\frac{9a}{4}.\) Solving gives \(a=8,\) and our desired exponential equation is \(\boxed{y=8\left(\frac{3}{2}\right)^x}.\)
ILL GIVE BRAINLESS DUE SOON

Answers
Answer:
Its C
Step-by-step explanation:
Please help!!!
Which figure has reflection symmetry?

Answers
Answer:
bottom right
Step-by-step explanation:
It can be split in half by an axis and remain congrugent
Answer:
The first figure.
Step-by-step explanation:
Because its edges are identical
\(.\)
HELP 100 POINTS WILL GIVE BRANLIEST IF ITS RIGHT LOOK IMAGE
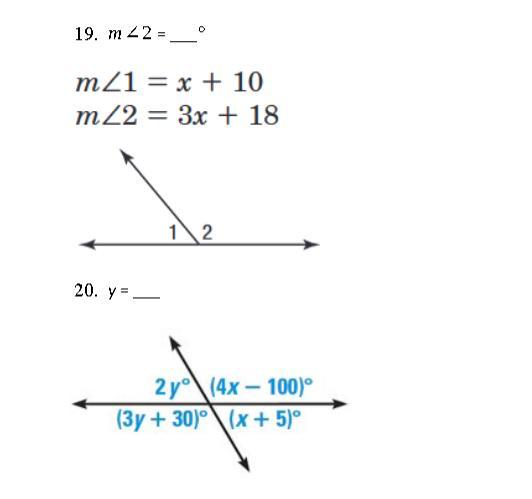
Answers
The value of \(m\angle2\) is \(132\) and the value of \(y\) is \(30\).
19) In this question given that,
\(m\angle1=x+10\)
\(m\angle2=3x+18\)
We have to find the value of \(m\angle2\).
As we know that the value of straight line is \(180^o\).
From the given figure we can see that
\(m\angle1+m\angle2=180^o\)
Now putting the value of \(m\angle1\) and \(m\angle2\) in the \(m\angle1+m\angle2=180^o\).
\(x+10+3x+18=180^o\)
Now simplifying the expression.
\(4x+28=180^o\)
Subtract \(28\) on both side
\(4x+28-28=180^o-28\)
\(4x=152\)
Divide by \(4\) on both side
\(\frac{4}{4}x=\frac{152}{4}\)
\(x=38\)
We have to find the value of \(m\angle2\).
As we know that \(m\angle2=3x+18\).
Now putting the value of \(x\) in the given value of \(m\angle2\).
\(m\angle2=3\times38+18\)
\(m\angle2=114+18\\\)
\(m\angle2=132\)
Hence, the value of \(m\angle2\) is \(132\).
20) In this question we have to find the value of \(y\).
As we know that the value of straight line is \(180^o\).
From the given figure we can see that
\(2y^o+(3y+30)^o=180^o\)
Now solving the expression to find the value of \(x\).
\(2y^o+3y^o+30^o=180^o\)
Simplifying the expression.
\(5y^o+30^o=180^o\)
Subtract \(30^o\) on both side
\(5y^o+30^o-30^o=180^o-30^o\)
Simplifying
\(5y^o=150^o\)
Divide by \(5\) on both side
\(\frac{5}{5}y^o=\frac{150^o}{5}\)
\(y^o=30^o\)
Hence, the value of \(y\) is \(30\).
To learn more about angle link is here
https://brainly.com/question/28451077
#SPJ1
Lillian has 8 jars each with 240 milliliters of apple cider vinegar. How many liters of vinegar is in all 8 jars?
Answers
Answer:
1.92 litres
Step-by-step explanation:
1l=1000ml
1 jar=240ml=0.24l
8 jars= 240x8=1920ml=1.92l
The median weekly income for a student who drops out of high school is 451. Someone with a bachelor's degree from college earns 1053 in that same week. Calculate each person's yearly income and then the difference between them.
Answers
The difference between their yearly incomes is $31,304.
To calculate each person's yearly income, we need to multiply their weekly income by the number of weeks in a year. Assuming there are 52 weeks in a year, the yearly income can be calculated as follows:
For the student who drops out of high school:
Yearly Income = Weekly Income x Number of Weeks
= 451 x 52
= 23,452
For someone with a bachelor's degree:
Yearly Income = Weekly Income x Number of Weeks
= 1053 x 52
= 54,756
The difference between their yearly incomes can be found by subtracting the student's yearly income from the bachelor's degree holder's yearly income:
Difference = Bachelor's Yearly Income - Student's Yearly Income
= 54,756 - 23,452
= 31,304
Therefore, the difference between their yearly incomes is $31,304.
It is important to note that these calculations are based on the given information and assumptions. The actual yearly incomes may vary depending on factors such as work hours, additional income sources, deductions, and other financial considerations.
Additionally, it is worth considering that educational attainment is just one factor that can influence income, and there are other variables such as experience, job type, and market conditions that may also impact individuals' earnings.
For more such answers on incomes
https://brainly.com/question/28414951
#SPJ8
Identify the Like Terms and Simplify:
3x + 5 - 7x + 4 - 2x - 8
Answers
Answer:
=−6x+1
Step-by-step explanation:
=3x+5+−7x+4+−2x+−8
=(3x+−7x+−2x)+(5+4+−8)
Alice spends $7 on lunch and $5.50 on a CD. She also buys 2 sweaters that each cost the same amount. Alice spends a total of $45. What is the cost of each shirt?
whoever gets it correct gets the brainlest
Answers
Steven wishes to save for his retirement by depositing $2,000 at the beginning of each year for thirty years. Exactly one year after his last deposit, he wishes to begin making annual level withdrawals until he has made twenty withdrawals and used up the savings. Find the amount of each withdrawal if the effective interest rate is 3% during the first thirty years but only 2% after that.
Answers
Step-by-step explanation:
i = interest 3% for 30 years
This is a simple dynamical system for whom the the solutions are given as
\(S=R[\frac{(i+1)^n-1}{i}](i+1)\)
putting values we get
S=2000[\frac{(1.03)^{30}-1}{0.03}](1.03)
= $98005.35
withdrawal of money takes place from one year after last payment
To determine the result we use the present value formula of an annuity date
\(P = R\frac{1-(1+i)^{-n}}{i}{i+1}\)
we need to calculate R so putting the values and solving for R we get
R= $6542.2356
0.9t
t² + 64
Find the time
The concentration of a drug t hours after being injected is given by C(t) =
when the concentration is at a maximum. Give your answer accurate to at least 2 decimal places.
hours.
Calculator
Submit Question
Answers
3What is the first step in solving the following equation?5-201 = 654.5Add 4.5 to both sidesSubtract 201 from both sidesDivide both sides by 65Multiply both sides by 4.5Add 201 to both sides
Answers
The given equation is
\(\frac{x}{4.5}-201=65\)First, we have to add 201 on each side.
\(\begin{gathered} \frac{x}{4.5}-201+201=65+201 \\ \frac{x}{4.5}=266 \end{gathered}\)Hence, the right answer is the last option.Find x and y in terms of a and b.
Sax + by = 0
x + y = 2
(x, y) =
(a + b)
Answers
From the second equation, we have y = 2 - x.
Substituting this into the first equation, we get:
Sax + b(2 - x) = 0
Expanding this equation, we get:
Sax + 2b - bx = 0
Rearranging the terms, we get:
x(Sa - b) = 2b
Dividing both sides by (Sa - b), we get:
x = 2b/(Sa - b)
Substituting this value of x into the second equation, we get:
2b/(Sa - b) + y = 2
Substituting y = 2 - x, we get:
2b/(Sa - b) + (2 - 2b/(Sa - b)) = 2
Simplifying this equation, we get:
4b/(Sa - b) = 2
Multiplying both sides by (Sa - b)/2, we get:
2b = (Sa - b)
Simplifying this equation, we get:
b = a/2
Substituting this value of b into the equation for x, we get:
x = 2b/(Sa - b) = 2(a/2)/(Sa - a/2) = a/(2S - 1)
Substituting these values of x and y into the given point (x, y) = (a + b), we get:
(a/(2S - 1), 2 - a/(2S - 1)) = (a + a/2, a/2)
Therefore, the solution is:
x = a/(2S - 1) and y = 2 - a/(2S - 1).
The perimeter of any rectangle in which the length is 4 more than twice the width is P = 6 w + 8 , where w is the width. Which formula can be used to find the width given the perimeter? Multiple choice question. cross out A) w = P − 4 3 cross out B) w = 1 6 P − 8 cross out C) w = − P + 8 6 cross out D) w = P − 8 6
Answers
Answer: option D
Step-by-step explanation:
Given equation:
P = 6 w + 8 [eq1]
l=2w+4 [where l is length]
using eq1 we have:
6w=P-8
w=(P-8)/6
hence option D
learn more about perimeter here:
https://brainly.com/question/28499208
#SPJ9
is my answer correct?
THE ONE-EYED JACK MINE INVESTIGATION
The abandoned One-Eyed Jack Mine is about 31 miles off the main road adjacent to the Salmon River Wilderness area. There is only a rutted dirt track left where the access road used to run. It is so steep that when we hiked up it we had to pause every fifty feet or so to catch our breath. It seemed impossible but 3- 5 miles further we found remnants of the old wagons, the mineshaft, and the mill. The gold ore found in this mine was embedded in quartz and prospectors used the mill to grind up the quartz and rinse it with acid in huge shallow vats that were agitated so that the gold would sink to the bottom and the quartz could be washed away.
One arrangement of equipment we noticed included a circular vat about 18 feet in diameter which must have been connected by a huge belt to a smaller circular drive wheel 10 feet in diameter. The distance between the wheel and the vat was 8 feet. The equipment had been partially pre-fabricated then carried up the hill piece by piece to be re-assembled on the spot. Just the belt to connect the vat to the drive wheel would have been a major burden. We wondered how many times they had to carry new ones up to replace it. Calculate the length of belt needed to go around the drive wheel and the vat.
Answers
Answer:
The circumference of the drive wheel is 10 feet * 3.14 = 31.4 feet.
The circumference of the vat is 18 feet * 3.14 = 56.52 feet.
The total length of belt needed to go around the drive wheel and the vat is 31.4 + 56.52 = 87.92 feet.
P.3 5. The figure shows the graph of
y= -kx² - 4x + m. It cuts the x-axis at two points A and B. Given that the graph passes through the points (4, -18) and (-2,30).
(a) Find the values k and m. (b) Hence, find the coordinates of A and B.
(c) C is a moving point on the above graph. When C is above the x-axis, find the maximum area of ABC.
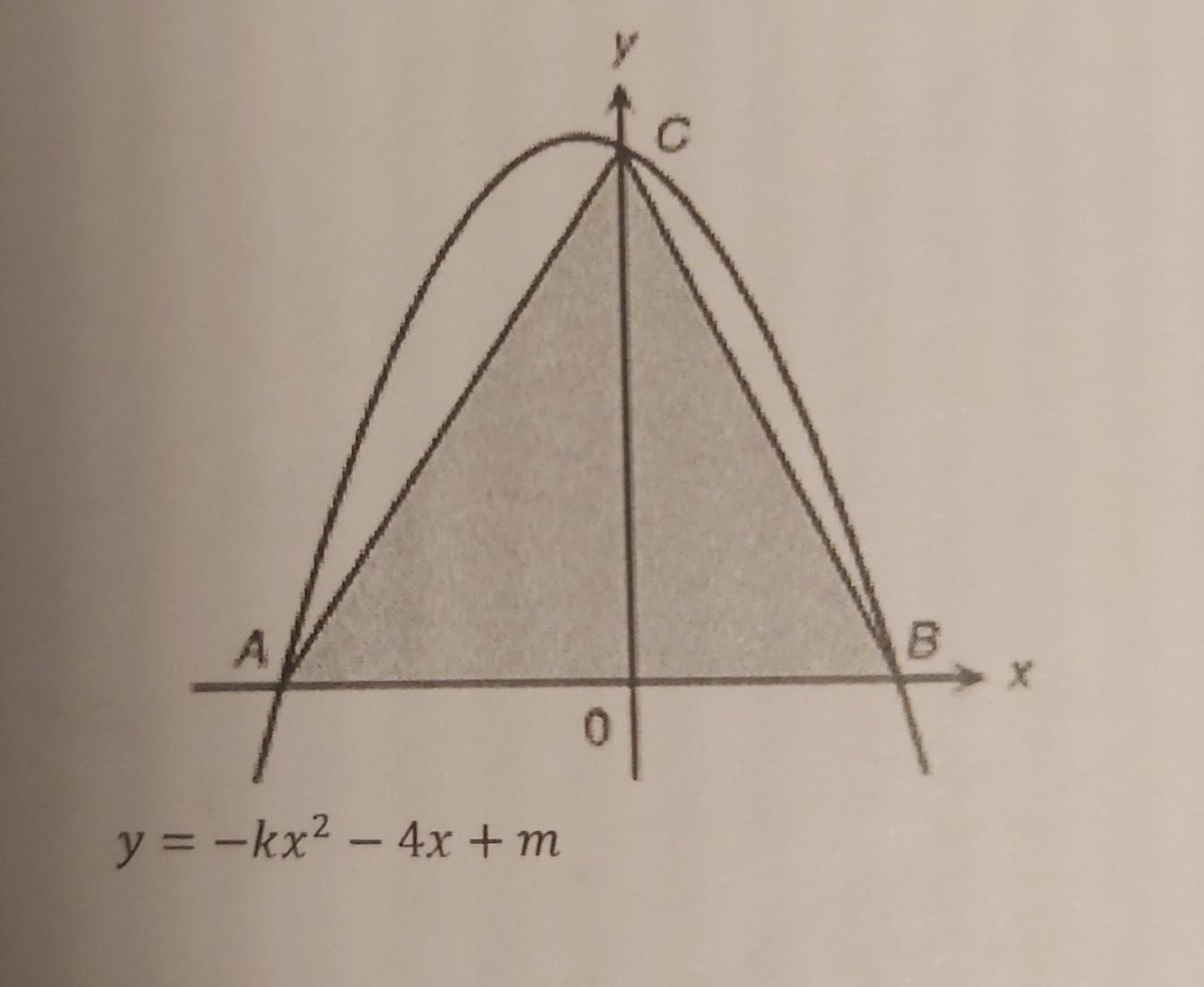
Answers
The required value of points A and B is given by \(x_{A,\:B}=\frac{-12\pm \:2\sqrt{466}}{2*5}\).
What is the graph?The graph is a demonstration of curves that gives the relationship between the x and y-axis.
Here,
The given equation is
y= -kx² - 4x + m
The above equation passes by points (4,-18) and (-2,30) So,
-18 = -k×4×4 - 4 × 4 + m
-18 = -16k - 16 + m
m - 16k = 2 - - - - - -(1)
Similarly,
m - 4k = 22 - - - - - - - (2)
Solving equations,
We get
k = 5/3 and m = 86/3
So the equation is given by,
y = -5/3x² - 4x + 86/3
Part (A)
Now, putting y = 0
5/3x² + 4x - 86/3 = 0
\(x_{A,\:B}=\frac{-12\pm \:2\sqrt{466}}{2*5}\)
Thus, the required value of points A and B is given by \(x_{A,\:B}=\frac{-12\pm \:2\sqrt{466}}{2*5}\).
Learn more about graphs here:
brainly.com/question/16608196
#SPJ1
PLEASE HELP. Will pick branliest!
Triangle ABC is similar to triangle WYZ. Find the value of the line segment WZ.

Answers
Answer:
WZ=4
Step-by-step explanation:
2/5=x/10
cross multiply
20=5x
x=4
Answer:
4, because 10/5 is 2, and then 2 * 2 is 4.
Plz help quickly kinda don’t understand it a bit

Answers
Answer:
Step-by-step explanation:
\(\text{The area of a circle is}\\ \\ A=\pi r^2\\ \\ \pi \approx 3.14,\ r=3ft\\ \\ A=3.14(3^2)\\ \\ A=3.14(9)\\ \\ A\approx 28.3ft^2\)
Anu was checking her emails she casually told her friend siting next to her the ratio of unread emails in my inbox is 4:1 The total number of emails is 120 what is the number of unread emails in her inbox
Answers
In a case whereby Anu was checking her emails and she casually told her friend siting next to her the ratio of unread emails in my inbox is ratio 4:1 where the total number of emails is 120 then the number of unread emails in her inbox is 96mails.
How can the unread mails be calculated?The concept that will be used here is ratio. An ordered pair of numbers a and b, represented as a / b, is a ratio if b is not equal to 0. A proportion is an equation that sets two ratios at the same value. For instance, you could express the ratio as follows: 1: 3 if there is 1 boy and 3 girls (for every one boy there are 3 girls)
The total mails in her box is 120
The we can represent the unread mails as 4x and read mails be 1x
This can be expressed as :
(4x+1x)=120mails
5x=120mails
x=120/5
x=24
This implies that the uread mails(4×24)
=96mails
Then the number of the read mail =(1×24)=24mails
Learn more about emails at:
https://brainly.com/question/20731943
#SPJ1
determine the answer to the following equation with correct number of significant figures: 2.02 8.102 - 0.0297
Answers
The solution is, B , is the correct answer is 10.0923.
What is Subtraction?Subtraction is the process of taking away a number from another. It is a primary arithmetic operation that is denoted by a subtraction symbol (-) and is the method of calculating the difference between two numbers.
here, we have,
given that,
the equation is, 2.02 + 8.102 - 0.0297
now, we have to solve it, by addition & subtraction.
we know,
First
2.02+8.102=10.122
Then 10.122-0.0297=10.0923
i.e. we get,
2.02 + 8.102 - 0.0297
=10.122-0.0297
=10.0923.
Hence, The solution is, B , is the correct answer is 10.0923.
To learn more on subtraction click:
brainly.com/question/2346316
#SPJ1
Suppose that the functions fand g are defined as follows.
f(x)=(4+x)(6+x)
g(x) = 1+x
Find (f/g)(-5)
Find all values that are NOT in the domain of f/g
Answers
(f/g)(-5) is equal to 1/4, and the value -1 is not in the domain of f/g.
To find (f/g)(-5), we need to substitute -5 into the functions f(x) and g(x) and then divide f(-5) by g(-5).
Given:
f(x) = (4+x)(6+x)
g(x) = 1+x
Substituting -5 into the functions:
f(-5) = (4+(-5))(6+(-5)) = (-1)(1) = -1
g(-5) = 1+(-5) = -4
Now, we can calculate (f/g)(-5):
(f/g)(-5) = f(-5) / g(-5) = -1 / -4 = 1/4
Therefore, (f/g)(-5) equals 1/4.
Now let's determine the values that are not in the domain of f/g. The values that are not in the domain of f/g are the values that make the denominator g(x) equal to zero. In this case, the denominator is g(x) = 1+x.
To find the values that make the denominator zero, we solve the equation:
1 + x = 0
Subtracting 1 from both sides, we get:
x = -1
So, the value x = -1 is not in the domain of f/g because it would make the denominator equal to zero.
for such more question on domain
https://brainly.com/question/16444481
#SPJ8
Given that x = -3, y = 7 and z = 10, fidn the value of the expression. 5(x squared - y)/z
Pls help
Answers
when we evaluate the given expression:
5*(x^2 - y)/z
in x = -3, y = 7 and z = 10 the value of the expression is 1.
How to find the value of the expression?Here we start with the expression:
5*(x^2 - y)/z
Where x, y, and z are called variables, meaning that can take any number we want.
And we want to evaluate this, given the values:
x = -3
y = 7
z = 10
Evaluating just means that we need to change the correspondent variables by the given numbers, if we do that in the given expression we will get:
5*( (-3)^2 - 7)/10
5*( 9 - 7)/10 = 5*(2)/10 = 10/10 = 1
So, we can see that when we evaluate the given expression in x = -3, y = 7 and z = 10 the value of the expression is 1.
If you want to learn more about evaluating expressions:
https://brainly.com/question/4344214
#SPJ1
write the english phrase as an algebraic expression. Let x represent the number
Answers
The english phrase "Seven less than four times a number" as an algebraic expression is 4x - 7
Writing the english phrase as an algebraic expressionFrom the question, we have the following parameters that can be used in our computation:
seven less than four times a number
Represent the number with x
So:
four times a number means 4x
So, we have
seven less than 4x
seven less than means - 7
So, we have
4x - 7
Hence, the english phrase as an algebraic expression is 4x - 7
Read more about expression at
brainly.com/question/4344214
#SPJ1
Complete question
write the english phrase as an algebraic expression. Let x represent the number
Seven less than four times a number
If the sum and product
of roots of a quadratic
equation are -7/2 and
5/2 respectively,then
the equation is :
Answers
Answer:
The equation is y = 2x² + 7x + 5
Step-by-step explanation:
In the quadratic equation y = ax² + bx + c
The roots of it are the values of x at y = 0The sum of the two roots = \(\frac{-b}{a}\)The product of the two roots = \(\frac{c}{a}\)∵ The sum of the roots is \(\frac{-7}{2}\)
∵ The product of the roots is \(\frac{5}{2}\)
→ By using the rules above
∴ \(\frac{-b}{a}\) = \(\frac{-7}{2}\)
∴ \(\frac{c}{a}\) = \(\frac{5}{2}\)
→ Compare between them
∴ a = 2
∴ -b = -7 ⇒ divide both sides by -1
∴ b = 7
∴ c = 5
∵ The form of the quadratic function is y = ax² + bx + c
→ Substitute the values of a, b, and c in it
∴ y = 2x² + 7x + 5
∴ The equation is y = 2x² + 7x + 5
WILL GIVE BRAINLIEST if you explain your answer!!

Answers
Answer:
x=-3
Step-by-step explanation:
You need to delete the root by ^2. First you need to leave it alone
\(\sqrt{x+7}-x=5\\\sqrt{x+7}=5-x\\(\sqrt{x+7} )^{2}=(5-x)^{2} \\x+7=25+10x+x^2\\x-10x=25+x^2-7\\-9x=18+x^2\\-x^2-9x-18=0\\-1(x^2+9x+18)=0\\x^2+9x+18=\frac{0}{-1}\\x^2+9x+18=0\\(x+6)(x+3)=0\\x+6=0 ===> x=-6\\x+3=0 ===> x=-3\\Checking\\\sqrt{-6+7}-(-6)=5===>\sqrt{1}+6=7\neq5 \\\\\sqrt{-3+7}-(-3)=5===>\sqrt{4}+3=5=5\\\\So \\x=-3\)
Write the equation of a line that goes through the points (-5,6) and (10,-6). The final answer should be in Slope Intercept Form

Answers
Answer:
\( y = -\frac{4}{5}x + 2 \)
Step-by-step explanation:
Find slope (m) using two points (-5, 6) and (10, -6).
\( slope (m) = \frac{y_2 - y_1}{x_2 - x_1} = \frac{-6 - 6}{10 - (-5)} = \frac{-12}{15} = -\frac{4}{5} \)
m = -⅘
To find y-intercept (b), substitute x = -5, y = 6, and m = ⅘ into y = mx + b
6 = (-⅘)(-5) + b
6 = 4 + b
6 - 4 = b (subtraction property of equality)
b = 2
To write the equation, substitute m = -⅘, and b = 2 into y = mx + b
The equation of the line would be:
✅\( y = -\frac{4}{5}x + 2 \)
The equation of a line that goes through the points (-5,6) and (10,-6 in slope-intercept form is \(y = -\frac 45x + 2\)
What is linear equation?A linear equation is an equation that have a constant rate of change or slope
From the question, we have the following ordered pairs
(x,y) = (-5,6) and (10,-6)
So, the slope (m) is then calculated as:
\(m =\frac{y_2 -y_1}{x_2 -x_1}\)
This gives
\(m =\frac{-6 - 6}{10 + 5}\)
Evaluate the differences
\(m =-\frac{12}{15}\)
Reduce the fraction
\(m =-\frac{4}{5}\)
The equation is then calculated as:
\(y = m(x -x_1) + y_1\)
So, we have:
\(y = -\frac 45(x + 5) + 6\)
Open the bracket
\(y = -\frac 45x -4 + 6\)
Evaluate the difference
\(y = -\frac 45x + 2\)
Hence, the equation in slope-intercept form is \(y = -\frac 45x + 2\)
Read more about linear equation at:
https://brainly.com/question/1884491
Please help asap …Write an equation of the line below

Answers
Answer: y-intercept = y= -1/2x, point-slope = (y-4)=-1/2(x+8)
Step-by-step explanation:
(X) + log (X+4)=log 32 for x
Answers
The value of x from the logarithmic expression is 4 and -8
Given the logarithmic expressionLogarithm are inverse of exponential function. Given the logarithmic function below;
log (X) + log (X+4)=log 32
Since positive will become multiplication, hence;
X(X+4) = 32
Expand
X^2 + 4x = 32
x^2 + 4x - 32 = 0
x^2 + 8x - 4x - 32 = 0
x(x + 8) - 4(x + 8) = 0
(x-4)(x+8) = 0
X = 4 and -8
Hence the value of x from the logarithmic expression is 4 and -8
Learn more on logarithmic expression here: https://brainly.com/question/25710806
#SPJ1