In 1990, the cost of tuition at a large Midwestern university was $94 per credit hour. In 2004, tuition had risen to $290 per credit hour.
Determine a linear function
C
(
x
)
to represent the cost of tuition as a function of
x
, the number of years since 1990.
Answers
The linear function c(x) to represent the cost of tuition as a function of "the number of years since 1990" denoted by "x" is \([c(x) = 14x+94]\).
As per the question statement, the cost of tuition at a large Midwestern university was $94 per credit hour in 1994 while it had risen to $290 per credit hour in 2004.
We are required to determine a linear function c(x) that represents the cost of tuition as a function of "the number of years since 1990", denoted by "x".
To solve this question, we need to know the equation of a line passing through two points (x₁, y₁) and (x₂, y₂) which goes as
\((y-y_{1} )=(\frac{y_{2} -y_{1} }{x_{2} -x_{1}})(x-x_{1})\).
Here, if we consider (x = 0) at 1990, c(x) = 94.
And since the standard form of conversion of functions into coordinate points goes as [y = f(x)], i.e., the ordinate is a function of the abscissa, therefore in this case, [y = c(x) = 94].
Thus, we can consider (x₁, y₁) as (0, 94).
Similarly, at 2004, [x = (2004-1990) = 14], and c(x) = 290, i.e.,
We can consider as (x₂, y₂) as (14, 290).
Using the values of (x₁, y₁) and (x₂, y₂), in the above mentioned standard equation of line passing through two points, we get,
\((y-94)=\frac{290-94}{14-0} (x-0)\\or, (y-94)=\frac{196}{14}x\\or,(y-94)=14x\\or,y=14x+94\).
Hence, the linear function c(x) that represents the cost of tuition as a function of "the number of years since 1990", denoted by "x" is \([c(x) = 14x+94]\).
Linear Function: In Mathematics, a function is an operator which when provided with a input, gives a certain output, and when a function can be depicted in form of a linear equation, it is known as a linear function.To learn more about Linear Functions, click on the link below.
https://brainly.com/question/21107621
#SPJ9
Related Questions
Using circles to model the ratios, divide both circles into
equal parts.
For the ratio 2 to 7,
parts should be shaded.
For the ratio 5:7,
parts should be shaded.
The ratio 2 to 7 is
the ratio 5:7.
Answers
By using circle model the images are attached below:
What is a circle model?A circle with a diameter of one has n firms distributed uniformly around it. In light of this, every company's distance from each of its closest neighbors is 1/n.
We must first create two circles in order to compare the ratios of 2 to 7 and 5:7 using a circle model.
Then, we must divide each circle into seven pieces.
We must shade 2 of the circle's total 7 portions in order to maintain the 2:7 ratio.
We must shade 5 of the circle's total 7 portions in order to maintain the 5:7 ratio.
As a result, the first circle symbolizes a 2:7 ratio, while the second circle a 5:7 ratio.
By using circle model the images are attached below:
To know more about circle model, visit:
https://brainly.com/question/29113869
#SPJ1

Answer: using circles to model the ratios, divide both circles into
7
equal parts.
For the ratio 2 to 7,
2
parts should be shaded.
For the ratio 5:7,
5
parts should be shaded.
The ratio 2 to 7 is
less than
the ratio 5:7
What number line shows the approximate location of V5

Answers
The number line that shows approximately the location of √5 would the number line in option D.
What is a number line?A number line is defined as the expression that can be used to illustrate the position of a given number which show either it is a positive or a negative number with one at the middle.
The given value is thus;
= √5 = 2.236067977 = 2.2
From the chosen number line, the dark dot is just few points after 2.
Learn more about number line here:
https://brainly.com/question/24644930
#SPJ1
write 15/7 as a mixed number
Answers
The result can be shown in multiple forms.
Exact Form:
15/7
Decimal Form:
2.142857
Mixed Number Form:
2 1/7
------------------------
Usually I try to explain what to do, but it's been a hot second from when I learned this. I uploaded a picture that might help.
This is a free tool for solving math problems if you ever need help: (no spaces or exclamation point) mat h way . co!m
------------------------
much love <333 good bye!!

a study of long-distance phone calls made from general electric reveled the length of the calls, in minutes, follows the normal probability distribution. the mean length of time per call was 4.5 minutes and the standard deviation was 0.70 minutes. what is the probability that calls last between 4.0 and 6.0 minutes?
Answers
The probability that calls last between 4.0 and 4.6 minutes will be around 0.4332.
we have to standardize the values and utilize the standard typical dispersion table or calculator.
To discover the z-scores for 4.0 and 6.0 minutes:
z1 = (4.0 - 6.0 ) / 0.70 = 2.8
z2 = (4.5 - 6.0 ) / 0.70= 2.1
Since Employing a standard ordinary conveyance table, we are able to discover the likelihood of the calls enduring between 4.0 and 4.6 minutes:
P(0 ≤ Z ≤ 2.1) = 0.4332
However the likelihood that calls final between 4.0 and 4.6 minutes is 0.4332, or around 0.4332.
To know more about probability refer to this :
brainly.com/question/24756209
#SPJ1
‼️‼️‼️WILL MARK BRAINLIEST, IF HELPFUL‼️‼️‼️

Answers
Like fractions, whatever you do to one you have to do to the other. On the table you can see how 2 turns to 8. It has been multiplied by 4, therefore we know to multiply 5*4 which gives us 20. Therefore, 8:20. Same stradegy can be applied to 20:50.
Answer:
Y = 5/2 X
Step-by-step explanation:
Number of Sculptures: 2, 8, 20
Number of paintings: 5, 20, 50
8 * 5/2 = 8 * 5/2
= 40/2
= 20
50 * 2/5 = 10 * 2
= 20
Assume X represents the number of sculptures
Y represents the number of paintings
Y = 5/2 X
Hope this helps!
Find the simple interest for a $3000 loan for 3 years at a rate of 5% (Formula: I=Prt)
Answers
To answer this, you use the formula \(I = Prt\) where
\(I\) is the simple interest that builds
\(P\) is the principal (AKA the amount invested/borrowed)
\(r\) is the interest rate per year
\(t\) is the lenght of the loan, in years.
In your situation:
\(\begin{aligned}I &= (\$3000)(5 \%/\text{year})(3 \text{ years})\\[0.5em]&= (3000)(0.05)(3)\\[0.5em]&= 450\end{aligned}\)
This means there'd be $450 of simple interest due at the end of 3 years.
Answer:
$450
Step-by-step explanation:
Interest= 3000(5%)(3)= $450
Common mistake: Do not use 36 as the time period. Only use the number of years, it the number of months.
d) Suppose you begin making a monthly payment of $75.00. Fill in the table.
Month Current balance
1
2
3
4
5
6
7
8
9
10
11
12
WYPIE
$2750.00
Interest
$45.38
Payment
$75.00
$75.00
$75.00
$75.00
$75.00
$75.00
$75.00
$75.00
$75.00
$75.00
$75.00
$75.00
Amount applied to principal
$29.62
Answers
Answer:
Step-by-step explanation:
Answer:
For month 1, the current balance is $2750.00, the interest is $45.38, and the payment is $75.00. The amount applied to principal is $29.62.
For the remaining months, the interest and payment amount will stay the same, but the current balance and amount applied to principal will change based on the previous month's numbers.
Point of view:
Here's your answer but I prefer you to focus and study hard because school isn't that easy. But i'm glad I could help you!
:)
Given the vertices, determine the quadrilateral's most specific classification.
A(5, -3) B(7, 1) C(9, -3) D(-7, 7)
Answers
A hospital employed 1,854 people one year and 2,003 the following year.
How many more people were employed the second year?
Answers
Answer:
149 more people.
Step-by-step explanation:
1. Subtract 2003 by 1854 and get 149
NEED ASaap 8th grade marth

Answers
Answer:
the answer is
y=3/2+4
Step-by-step explanation:
4 is found on the y-axis and 3/2 is 1,5 and it looks like its going 1,5 steps up
3(x-7)= -4(5 -x) - (x + 2)
Answers
Step-by-step explanation:
I think so the question is incorrect or I can't solve it.
Elena drank 5 bottles of water over 7 volleyball practices. How much water did Elena drink each practice if she drank the same amount each time?
Please have good explanation
Answers
Answer:
Step-by-step explanation:
If you would like to know how much water did Elena drink each practice if she drank the same amount each time, you can calculate this using the following steps:
5 bottles of water ... 7 practices
x bottles of water = ? ... 1 practice
5 * 1 = 7 * x
5 = 7 * x /7
x = 5/7 bottle of water
The correct result would be 5/7 bottle of water.
The area of a rectangle is given by the function A(x) = 2x3 + 6x2 + 5x + 15. If the length is defined by x + 3, what is the width of the rectangle?
Answers
Answer:
2x² +5
Step-by-step explanation:
You want the width of a rectangle with a length of x+3 and an area of A(x) = 2x³ +6x² +5x +15.
AreaThe area is the product of length and width, so the width will be ...
A = LW
W = A/L = (2x³ +6x² +5x +15)/(x +3)
The cubic expression can be factored by grouping, so we have ...
Area = (2x³ +6x²) +(5x +15)
= 2x²(x +3) +5(x +3)
= (2x² +5)(x +3)
Then the width is ...
\(\text{width}=\dfrac{(x+3)(2x^2+5)}{x+3}=\boxed{2x^2+5}\)
The width of the rectangle is 2x² +5.
<95141404393>
Please help!!
Enter the correct answer in the box.
Function g is the result of these transformations on the parent sine function:
• vertical stretch by a factor of 3
• horizontal shift left
units
• vertical shift down 4 units
Substitute the values of A, C, and D to complete the equation modeling function g.
Answers
Answer:
By substituting the values of A, C, and D the equation modelling the function is;g(x) = 3·sin(x - π/2) - 4
Step-by-step explanation:
From the given information, we have;The vertical stretch of the sine function = 3 × The parent function∴ A = 3Given that the horizontal shift left = π/2 units, (from an online source with similar question)The vertical shift down = 4 unitsThe given function, g is g(x) = A·sin(x + C) + DWhere;A = The amplitude = The maximum displacement from the rest or equilibrium position = 3C = The horizontal shift = -π/2 (The negative sign is for the shifting to the left)D = The vertical shift = -4 (The negative sign is for a shift in the downward direction)Therefore, the equation modelling the function is;g(x) = 3·sin(x - π/2) - 4
What is the M.A.D. (mean absolute deviation) of the following data set?
8 9 9 7 8 6 9 8
Answers
The mean absolute deviation is 0.75
How to determine the mean absolute deviationTo calculate the mean absolute deviation (M.A.D.), you need to find the average of the absolute differences between each data point and the mean of the data set
From the information given, we have that the data set is;
8 9 9 7 8 6 9 8
Let's calculate the mean, we get;
Mean = (8 + 9 + 9 + 7 + 8 + 6 + 9 + 8) / 8
Mean = 64 / 8
Divide the values
Mean = 8
Let's determine the absolute difference, we get;
Absolute differences=
|8 - 8| = 0
|9 - 8| = 1
|9 - 8| = 1
|7 - 8| = 1
|8 - 8| = 0
|6 - 8| = 2
|9 - 8| = 1
|8 - 8| = 0
Find the mean of the absolute differences:
Average of absolute differences = (0 + 1 + 1 + 1 + 0 + 2 + 1 + 0) / 8
Absolute difference = 6 / 8 = 0.75
Learn more about mean absolute deviation at: https://brainly.com/question/447169
#SPJ1
Find the SURFACE AREA of this composite solid.
Answers
FINDING THE SURFACE AREA OF A COMPOSITE SOLID
About "Finding the surface area of a composite solid"
Finding the surface area of a composite solid :
A composite solid is made up of two or more solid figures.
To find the surface area of a composite solid, find the surface area of each figure. Subtract any area not on the surface.
Finding the surface area of a composite solid - Examples
Example 1 :
Daniel built the birdhouse shown below. What was the surface area of the birdhouse before the hole was drilled ?
Solution :
Step 1 :
Identify the important information.
• The top is a triangular prism with h = 24 cm. The base is a triangle with height 8 cm and base 30 cm.
• The bottom is a rectangular prism with h = 18 cm. The base is a 30 cm by 24 cm rectangle.
• One face of each prism is not on the surface of the figure.
Step 2 :
Find the surface area of each prism.
Add the areas. Subtract the areas of the parts not on the surface.
Step 3 :
Find the area of the triangular prism.
Perimeter = 17 + 17 + 30 = 64 cm
Base area = (1/2)(30)(8) = 120 sq.cm
Surface area = Ph + 2B
Surface area = 64(24) + 2(120)
Surface area = 1,776 sq.cm
Step 4 :
Find the area of the rectangular prism.
Perimeter = 2(30) + 2(24) = 108 cm
Base area = 30(24) = 720 sq.cm
Surface area = Ph + 2B
Surface area = 108(18) + 2(720)
Surface area = 3,384 sq.cm
Step 5 :
Add. Then subtract twice the areas of the parts not on the surface.
Surface area = 1,776 + 3,384 - 2(720) = 3,720 sq.cm
The surface area before the hole was drilled was 3,720 sq.cm.

The surface area before the hole was drilled was; 3,720 sq.cm.
What is composite solid?A composite solid is made up of two or more solid figures.
To determine the surface area of a composite solid, find the surface area of each figure. Subtract any area not on the surface.
Given that the top is a triangular prism with h = 24 cm. The base is a triangle with height 8 cm and base 30 cm.
The bottom is a rectangular prism with h = 18 cm.
The base is a 30 cm x 24 cm rectangle.
One face of each prism is not on the surface of the figure.
Then the surface area of each prism.
Add the areas. Subtract the areas of the parts not on the surface.
The area of the triangular prism.
Perimeter = 17 + 17 + 30 = 64 cm
Base area = (1/2)(30)(8) = 120 sq.cm
Surface area = Ph + 2B
Surface area = 64(24) + 2(120)
Surface area = 1,776 sq.cm
Now the area of the rectangular prism.
Perimeter = 2(30) + 2(24) = 108 cm
Base area = 30(24) = 720 sq.cm
Surface area = Ph + 2B
Surface area = 108(18) + 2(720)
Surface area = 3,384 sq.cm
Now,
Surface area = 1,776 + 3,384 - 2(720) = 3,720 sq.cm
Learn more about the area;
https://brainly.com/question/1658516
#SPJ2

What type of angles are labeled and what is the value of m? Show your work.

Answers
Answer: I believe
M = 80
Step-by-step explanation:
100 - 20 = 80
In a sample of 100 steel wires the average breaking strength is 50 kN, with a standard deviation of 2 kN. a. Find a 95% confidence interval for the mean breaking strength of this type of wire. b. Find a 99% confidence interval for the mean breaking strength of this type of wire. c. An engineer claims that the mean breaking strength is between 49.7 kN and 50.3 kN. With what level of confidence can this statement be made? d. How many wires must be sampled so that a 95% confidence interval specifies the mean breaking strength to within ±0.3 kN? e. How many wires must be sampled so that a 99% confidence interval specifies the mean breaking strength to within ±0.3 kN?
Answers
Answer:
.
Step-by-step explanation:
1.
Alpha = 0.05. alpha/2 = 0.025
Under the z table
Z 0.025 = 1.96
50+-1.96(2/√100)
= 50+-0.39
50+0.39 = 50.39
50-0.39 = 49.61
2.
At 99%
Alpha = 0.01
Alpha/2 = 0.005
In z table
= 2.58
50+-(2.58)(2√100)
= 50 +- 0.52
= 50+0.52 = 50.52
50 - 52 = 49.48
Please check attachment for answers 3 to 5. The test editor did not work properly. It kept flagging some of my typed content.


Using the z-distribution, it is found that:
a) The 95% confidence interval for the mean breaking strength of this type of wire, in kN, is (49.61, 50.39).
b) The 99% confidence interval for the mean breaking strength of this type of wire, in kN, is (49.49, 50.52).
c) The confidence level is of 86.64%.
d) 171 wires must be sampled.
e) 295 wires must be sampled.
We are given the standard deviation for the population, which is why the z-distribution is used to solve this question.
The information given is:
Sample mean of \(\overline{x} = 50\). Population standard deviation of \(\sigma = 2\). Sample size of \(n = 100\).The confidence interval is:
\(\overline{x} \pm z\frac{\sigma}{\sqrt{n}}\)
The margin of error is of:
\(M = z\frac{\sigma}{\sqrt{n}}\)
Item a:
The first step is finding the critical value, which is z with a p-value of \(\frac{1 + \alpha}{2}\), in which \(\alpha\) is the confidence level.
In this problem, \(\alpha = 0.95\), thus, z with a p-value of \(\frac{1 + 0.95}{2} = 0.975\), which means that it is z = 1.96.
Hence, the interval is:
\(\overline{x} - z\frac{\sigma}{\sqrt{n}} = 50 - 1.96\frac{2}{\sqrt{100}} = 49.61\)
\(\overline{x} + z\frac{\sigma}{\sqrt{n}} = 50 + 1.96\frac{2}{\sqrt{100}} = 50.39\)
The 95% confidence interval for the mean breaking strength of this type of wire, in kN, is (49.61, 50.39).
Item b:
\(\alpha = 0.99\), thus, z with a p-value of \(\frac{1 + 0.99}{2} = 0.995\), which means that it is z = 2.575.
\(\overline{x} - z\frac{\sigma}{\sqrt{n}} = 50 - 2.575\frac{2}{\sqrt{100}} = 49.49\)
\(\overline{x} + z\frac{\sigma}{\sqrt{n}} = 50 + 2.575\frac{2}{\sqrt{100}} = 50.52\)
The 99% confidence interval for the mean breaking strength of this type of wire, in kN, is (49.49, 50.52).
Item c:
The margin of error is:
\(M = \frac{50.3 - 49.7}{2} = 0.3\)
Hence:
\(M = z\frac{\sigma}{\sqrt{n}}\)
\(0.3 = z\frac{2}{\sqrt{100}}\)
\(0.2z = 0.3\)
\(z = 1.5\)
z = 1.5 has a p-value of 0.9332, hence:
\(\frac{1 + \alpha}{2} = 0.9332\)
\(1 + \alpha = 2(0.9332)\)
\(\alpha = 0.8664\)
The confidence level is of 86.64%.
Item d:
This is n for which M = 0.3, with z = 1.96, hence:
\(M = z\frac{\sigma}{\sqrt{n}}\)
\(0.3 = 1.96\frac{2}{\sqrt{n}}\)
\(0.3\sqrt{n} = 1.96(2)\)
\(\sqrt{n} = \frac{1.96(2)}{0.3}\)
\((\sqrt{n})^2 = \left(\frac{1.96(2)}{0.3}\right)^2\)
\(n = 170.7\)
Rounding up, 171 wires must be sampled.
Item e:
Now z = 2.575, hence:
\((\sqrt{n})^2 = \left(\frac{2.575(2)}{0.3}\right)^2\)
\(n = 294.7\)
Rounding up, 295 wires must be sampled.
A similar problem is given at https://brainly.com/question/25325640
The number of bank robberies that occur in Lagos is modeled to be Poisson distributed with mean of 1.8 per day. Find the probability of getting exactly three robberies in a day.
Answers
The Poisson distribution is a discrete distribution that calculates the likelihood that a certain number of events will occur within a certain amount of time.
The probability of getting exactly three robberies in a day is 0.1607.
What is meant by poison distribution?The Poisson distribution is a discrete probability distribution used in probability theory and statistics to express the likelihood that a given number of events will occur within a specified time or space interval if they occur at a known constant mean rate and regardless of the interval since the last event.
The Poisson distribution is a discrete distribution that calculates the likelihood that a certain number of events will occur within a certain amount of time.
In the poison distribution a discrete random variable X has the following probability mass function,
\($P(X=x)=\frac{e^{-\lambda} \cdot \lambda^x}{x !}$\), where \($\lambda$\) is the mean of the distribution and \($x=0,1,2,3 \ldots \ldots$\)
Given that \($\lambda=1.8$\)
The required probability, \($P(X=3)=\frac{e^{-1.8} .(1.8)^3}{3 !}=0.1607$\)
Therefore, the probability of getting exactly three robberies in a day is = 0.1607.
To learn more about poison distribution refer to:
https://brainly.com/question/9123296
#SPJ9
A circle has a radius of 8 inches. What is the area of the largest square that can fit inside the circle?
Answers
Answer:
32
Step-by-step explanation:
The largest square possible is if the diagonal of the square = 8
The sides would \(8/\sqrt{2}\) or \(4\sqrt{2}\) because of 45 45 90 triangle
\(\frac{8}{\sqrt{2} } *\frac{8}{\sqrt{2} } = 64/2 = 32\)
Hope this helps :)
Have a great day!
Use intercepts to graph the linear equation 3x - y = -5.
x intercept
y intercept
step by step
Answers
Answer:
x intercept =(-5/3,0)
y intercept = (0,5)
Step-by-step explanation:
FOR THE X INTERCEPT:
-plug 0 in for the y value because the y value is 0 at the x intercept.
* 3x-0=-5 ---> 3x=-5 -----> x=-5/3 while y = 0
FOR THE Y INTERCEPT
-do the same thing as the x intercept, but instead of making y 0, make x 0.
* 3(0) -y=-5 ----> 0-y=-5 -----> -y=-5 ------->y=5 while x=0
An athlete eats 75 g of protein per day while training. How much protein will she eat during 21 days of training? Write your answer in kilograms.
Answers
Answer:
1.575 kg
Step-by-step explanation:
75g x 21
1575 g
convert to kg
1.575 kg
Brainliest Appreciated!
Which expressions are less than 7/8? Choose2 answers 7/8 x 9/19 7/8 x 3/4 7/8 x 9/9 7/8 x 4/3
Answers
The two expressions that are less than 7/8 are 7/8 x 9/19 and 7/8 x 3/4.
To determine which expressions are less than 7/8, we can compare them individually to 7/8 and evaluate their values.
Let's consider each expression one by one:
7/8 x 9/19:
To compare this expression to 7/8, we multiply the fractions:
(7/8) x (9/19) = 63/152.
Since 63/152 is less than 7/8, this expression is less than 7/8.
7/8 x 3/4:
Multiplying the fractions:
(7/8) x (3/4) = 21/32.
Since 21/32 is less than 7/8, this expression is less than 7/8.
7/8 x 9/9:
The fraction 9/9 simplifies to 1, so the expression becomes:
(7/8) x 1 = 7/8.
Since 7/8 is equal to 7/8 (not less than), this expression is not less than 7/8.
7/8 x 4/3:
Multiplying the fractions:
(7/8) x (4/3) = 28/24.
We can simplify 28/24 to 7/6.
Since 7/6 is greater than 7/8, this expression is not less than 7/8.
Therefore, the two expressions that are less than 7/8 are 7/8 x 9/19 and 7/8 x 3/4.
for such more question on expressions
https://brainly.com/question/12270624
#SPJ8
find an expression in terms of n for the nth term of this sequence, 15,19,25,33,43
Answers
Answer:
Hello,
Step-by-step explanation:
P(n)=ax²+bx+c (quadratic sequence)
with a=1,b=1,c=13
\(\\\boxed{u_n=n^2+n+13}\\\)
Answer:
tₙ = n² + n + 13=============================
Given sequence:
15, 19, 25, 33, 43, ...We can see this not AP or GP as the difference or ratio of consecutive terms is not common.
But we can see the difference between terms has common difference of 2:
19 - 15 = 425 - 19 = 633 - 25 = 843 - 33 = 10and
10 - 8 = 28 - 6 = 26 - 4 = 2It means the sequence is of the second degree, in other words it is quadratic.
In general it is of the form:
tₙ = an² + bn + c, where a, b, c are coefficients, n - is the number of the terms.Use the terms of the given sequence to work out unknown coefficients.
t₀ = 15 - (4 - 2) = 15 - 2 = 13
a(0)² + b(0) + c = 13c = 13It gave us the value of c.
t₁ = 15
a(1)² + b(1) + c = 15a + b + c = 15a + b + 13 = 15a + b = 2t₂ = 19
a(2)² + b(2) + c = 194a + 2b + c = 194a + 2b + 13 = 194a + 2b = 6Compare the last two equations and solve for a and b:
a = 2 - b4(2 - b) + 2b = 68 - 4b + 2b = 62b = 8 - 62b = 2b = 1Then
a = 2 - 1 a = 1So we know the coefficients:
a = 1, b = 1, c = 13The nth term equation is:
tₙ = n² + n + 13PLEASE HELP!! What is the surface area of the cone?
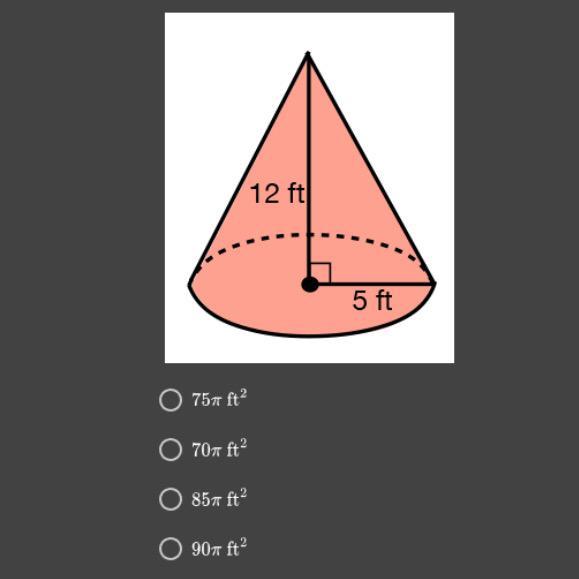
Answers
Hope this helped
Which of the following is a form of the law of cosines?
A. (2 - 2 + c2 + 2bc.COS A
B. Q2 = 32 - c2 + 2bc.cos A
C. b = Q? + c2 - 2ac-COS B
D. 32 = c++ C2 - 2ac.cosB
Please select the best answer from the choices provided
Answers
Evaluate 4(b + 1)² if b = 4.
Answers
4( 4+1)’2
add 4+1 to get 5
the equation now is 4(5)’2
multiple 5x5 to get rid of the exponent.
4(25)
4x25= 100
your answer is 100
Answer:
68
Step-by-step explanation:
4(4 + 1)²
4(16 + 1)
64 + 4
68
rewrite the fractions 3/4 and 7/10 as fractions with a least common denominator. a. 15/20 and 14/20b. 60/80 and 56/80c. 30/40 and 28/40d. 3/20 and 7/20
Answers
The rewritten fractions are 15/20 and 14/20. The correct answer is (a) 15/20 and 14/20.
To rewrite the fractions 3/4 and 7/10 with a least common denominator, follow these steps:
1. Find the least common multiple (LCM) of the denominators 4 and 10.
The LCM is the smallest number that both denominators can divide into.
In this case, the LCM is 20.
2. Rewrite each fraction with the new denominator (20) by multiplying the numerator and the denominator of each fraction by the necessary factor to reach the LCM.
For 3/4:
(3 * 5)/(4 * 5) = 15/20
For 7/10:
(7 * 2)/(10 * 2) = 14/20.
For similar question on fractions.
https://brainly.com/question/20712359
#SPJ11
make e the subject
e-5=2f
Answers
Answer:
e-5=2f
take '-5' to the other side where '2f' is
e=2f+5
2.) Ms. Baker is out today. When she returns she hopes to see 100% of her 70
students to have completed and turned their work assigned by the sub. How
many students does Ms. Baker hope have their work assigned by the sub
completed and turned in?
Answers
Answer:
70
Step-by-step explanation:
100% means all of them.