Answers
Related Questions
Find the average value of the function over the given interval. (Round your answer to three decimal places.)
f(x) = 6e^x, [−3, 3]
=
Find all values of x in the interval for which the function equals its average value. (Enter your answers as a comma-separated list. Round your answers to three decimal places.) x=
Answers
The only value of x in the interval [-3, 3] for which the function equals its average value is approximately x = 2.984.
What is integration?
Integration is a mathematical operation that is the reverse of differentiation. Integration involves finding an antiderivative or indefinite integral of a function.
To find the average value of the function f(x) = 6e^x over the interval [-3, 3], we need to evaluate the definite integral of f(x) over that interval and divide the result by the length of the interval:
Average value = (1/(3-(-3))) * ∫[−3, 3] 6e^x dx
= (1/6) * [\(6e^x\)] from -3 to 3
= (1/6) * (\(6e^3\) - \(6e^{(-3)}\))
≈ 118.936
Therefore, the average value of the function over the given interval is approximately 118.936.
To find all values of x in the interval [-3, 3] for which the function equals its average value, we need to solve the equation f(x) = 118.936, which means:
\(6e^x\) = 118.936
Dividing both sides by 6, we get:
\(e^x\) = 19.823666...
Taking the natural logarithm of both sides, we get:
x = ln(19.823666...)
≈ 2.984
Therefore, the only value of x in the interval [-3, 3] for which the function equals its average value is approximately x = 2.984.
To learn more about integration from the given link:
brainly.com/question/18125359
#SPJ4
Compare interior intersections and
exterior intersections. How are they the
same? How are they different?
Answers
Answer:
Interior intersections are those intersecitons inside the main figure. For example, the intersection between two chords of a circle, that represents an interior intersection.
Exterior interseciton are those intersections which happens outside the figure, for example, the intersection of two tangent lines of a circle.
Basically, they are similiar, because both type of intersections are formed by the encounter between two lines or segments.
However, they are different, because each type is formed at different parts of the figure, one inside and one outside.
solve the 3 × 3 system shown below. enter the values of x, y, and z. x 2y – z = –3 (1) 2x – y z = 5 (2) x – y z = 4
Answers
The solution to the given system of equations is x = 2, y = -1, and z = 1.
What are the values of x, y, and z that solve the given system of equations?To solve the system of equations, we can use methods such as substitution or elimination. Here, we will use the method of elimination to find the values of x, y, and z.
First, let's eliminate the variable x by multiplying equation (1) by 2 and equation (3) by -1. This gives us:
2x + 4y - 2z = -6 (4)
-x + y - z = -4 (5)
Next, we can subtract equation (5) from equation (4) to eliminate the variable x:
5y - z = 2 (6)
Now, we have a system of two equations with two variables. Let's eliminate the variable z by multiplying equation (2) by 2 and equation (6) by 1. This gives us:
4x - 2y + 2z = 10 (7)
5y - z = 2 (8)
Adding equation (7) and equation (8), we can eliminate the variable z:
4x + 5y = 12 (9)
From equation (6), we can express z in terms of y:
z = 5y - 2 (10)
Now, we have a system of two equations with two variables again. Let's substitute equation (10) into equation (1):
x + 2y - (5y - 2) = -3
x - 3y + 2 = -3
x - 3y = -5 (11)
From equations (9) and (11), we can solve for x and y:
4x + 5y = 12 (9)
x - 3y = -5 (11)
By solving this system of equations, we find x = 2 and y = -1. Substituting these values into equation (10), we can solve for z:
z = 5(-1) - 2
z = -5 - 2
z = -7
Therefore, the solution to the given system of equations is x = 2, y = -1, and z = -7.
Learn more about: Equations,
brainly.com/question/29657983
#SPJ11
HELP PLEASE this is worth a lot I’ll mark as Brainlist

Answers
So it would be an arrow pointing the the right with a closed circle on -2
I hope this will help you!
thirty-five percent of us adults have little confidence in their cars. you randomly select ten us adults. find the probability that the number of us adults who have little confidence in their cars is (1) exactly six and then find the probability that it is (2) more than 7.
Answers
1) Probability that exactly 6 adults have little confidence in their cars is 0.0689 .
2) Probability that more than 7 adults have little confidence in their cars is 0.005 .
Given details about US adults:
Adults having little confidence in their cars = 0.35
Sample size = 10
1)
Probability that exactly 6 adults have little confidence in their cars.
Binomial expression = \(nC_r(p)^r(1-p)^{n-r}\)
Here,
n = 10
p = 0.35
r = 6
Substitute the values in the binomial expression.
\(P(X = 6) = 10C_6(0.35)^6(1-0.35)^{10-6}\\P(X = 6) = 10C_6 (0.00183)(0.178)\\P(X= 6) = 0.0689\)
2)
Probability that more than 7 adults have little confidence in their cars.
Binomial expression = \(nC_r(p)^r(1-p)^{n-r}\)
Here,
n = 10
p = 0.35
r = 6
Substitute the values,
\(P(X > 7) = P(X = 8) + P(X = 9) + P(X = 10)\)
\(P(X > 7) = 10C_8(0.35)^8(1-0.35)^{10-8}+ 10C_9(0.35)^9(1-0.35)^{10-9}+ 10C_{10}(0.35)^{10}(1-0.35)^{10-10}\\P(X > 7) = 0.0043 + 0.0005 + 0.00003\\P(X > 7) = 0.005\)
Know more about probability,
https://brainly.com/question/32117953
#SPJ12
Writing The graph shows a proportional relationship between the variables y and x. Write an equation to model
the relationship. Use pencil and paper. Explain how you know there is a proportional relationship if you are given
either an equation or a graph.
the equation y= (blank) models the relationship.
the graph picture is the one that will help you figure it out

Answers
Answer:
y x
..........
....................
consider the natural numbers from 1 to 25. Write the prime numbers between 1 to 25. What fractions of these natural numbers are prime numbers?
Answers
Step-by-step explanation:
Natural numbers are numbers that include positive integers.
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25
Prime numbers are numbers that are greater than 1 and has only two factors
2,3,5,7,11,13,17,19,23
What Fractions of natural number are prime number?
9/25
Easy 30!! Can u Check if i got it right?
Divide (20x8y3 − 12x5y2) ÷ (−4x2y).
−5x6y3 + 3x3y2
5x6y3 − 3x3y2
−5x6y2 + 3x3y
5x6y2 − 3x3y
itk is C;
−5x6y2 + 3x3y
Answers
The result of the division based on the exponent will be C. −5x6y2 + 3x3y.
How to explain the valueWhen dividing with the same base, you subtract the exponents. So, for the x terms, you subtract the exponent of x in the denominator (-2) from the exponent of x in the numerator (8 - 5 = 3). Similarly, for the y terms, you subtract the exponent of y in the denominator (1) from the exponent of y in the numerator (3 - 2 = 1).
Therefore, the result is -5xy²+ 3x(5-2), which simplifies to -5xy² + 3x³y.
Thus, the correct answer is −5x6y2 + 3x3y.
Learn more about exponents on
https://brainly.com/question/13669161
#SPJ1
The weekly wages paid to the workers at a factory are approximately normally distributed with mean $405 and standard deviation $5. If a randomly selected group of 16 workers from the factory is taken, find the probability that their mean weekly wage will be within $3 of the population mean wage. Give your answer correct to two significant figures.
Answers
The probability that the mean weekly wage of a randomly selected group of 16 workers from the factory will be within $3 of the population mean wage is 0.98
To solve this problem,
We can use the central limit theorem which states that the sample means from a large sample will be approximately normally distributed with a mean equal to the population mean and a standard deviation equal to the population standard deviation divided by the square root of the sample size.
First, we need to find the standard error of the mean, which is equal to the standard deviation divided by the square root of the sample size:
Standard error of the mean = 5 / sqrt(16) = 1.25
Next, we need to find the z-score for the lower and upper bounds of the sample mean:
lower z-score = (402 - 405) / 1.25 = -2.4
upper z-score = (408 - 405) / 1.25 = 2.4
We can use a standard normal distribution table or a calculator to find the probabilities associated with these z-scores:
lower probability = 0.0082
upper probability = 0.9918
To find the probability that the sample mean is within $3 of the population mean we need to subtract the lower probability from the upper probability:
Probability = 0.9918 - 0.0082 = 0.9836
For similar question on probability:
https://brainly.com/question/23044118
#SPJ11
find the exact values of the sine, cosine, and tangent of the angle. 255° = 300° − 45°
Answers
The exact values of the sine, cosine, and tangent of the angle 255° are -1/√2, 1/√2, and -1, respectively.
To find the exact values of the sine, cosine, and tangent of the angle 255°, we can use the identity that relates the trigonometric functions of an angle to the trigonometric functions of its complement.
By expressing 255° as the sum of 300° and -45°, we can determine the exact values of the trigonometric functions for the given angle.
We know that the sine, cosine, and tangent of an angle are periodic functions, repeating every 360 degrees. To find the exact values of the trigonometric functions for 255°, we can express it as the sum of 300° and -45°, where 300° is a multiple of 360°.
Since the sine, cosine, and tangent functions are odd or even functions, we can use the values of the trigonometric functions for 45° to determine the values for -45°.
For 45°:
sin(45°) = cos(45°) = 1/√2
tan(45°) = 1
Since cosine is an even function, cos(-45°) = cos(45°) = 1/√2.
Since sine is an odd function, sin(-45°) = -sin(45°) = -1/√2.
Using the definition of tangent as the ratio of sine to cosine, tan(-45°) = sin(-45°) / cos(-45°) = (-1/√2) / (1/√2) = -1.
Therefore, for the angle 255°:
sin(255°) = -1/√2
cos(255°) = 1/√2
tan(255°) = -1
Learn more about trigonometric functions here:
brainly.com/question/28483432
#SPJ11
Simplify 6.4k + 2.8 – 0.75 + 1.8k.
Answers
Answer:
8.2k +2.05
Step-by-step explanation:
Which equation is a point slope form equation for line AB?
Responses
y+5=−2(x−2)
y plus 5 equals negative 2 left parenthesis x minus 2 right parenthesis
y+6=−2(x−1)
y plus 6 equals negative 2 left parenthesis x minus 1 right parenthesis
y+2=−2(x−5)
y plus 2 equals negative 2 left parenthesis x minus 5 right parenthesis
y+1=−2(x−6)
y minus 1 equals negative 2 left parenthesis x minus 6 right parenthesis
A graph with a line running through point A, with coordinates (1, 6), and point B, with coordinates (5, -2)
Answers
Answer:
Option 3
Step-by-step explanation:
The slope is \(\frac{-2-6}{5-1}=-2\).
The equation of the line through \((x_1, y_1)\) with slope \(m\) is \(y-y_1=m(x-x_1)\).
y-6=-2(x-1) is the equation is a point slope form equation for line AB
What is Slope of Line?The slope of the line is the ratio of the rise to the run, or rise divided by the run. It describes the steepness of line in the coordinate plane.
The slope intercept form of a line is y=mx+b, where m is slope and b is the y intercept.
The slope of line passing through two points (x₁, y₁) and (x₂, y₂) is
m=y₂-y₁/x₂-x₁
point A, with coordinates (1, 6), and point B, with coordinates (5, -2)
m=-2-6/5-1
m=-8/4
=-2
So slope is -2.
The point slope intercept of line is
y-y₁=m(x-x₁)
y-6=-2(x-1)
Hence y-6=-2(x-1) is the equation is a point slope form equation for line AB
To learn more on slope of line click:
https://brainly.com/question/14511992
#SPJ2
Is the line of best fit accurate for the data shown?
(A) Yes, because it touches the y-axis
(B) Yes, because there are about the same number of points above the line as below it
(C) No, because the line does not touch any points
(D) No, because the line should touch every point

Answers
Bev has to trim her grandma's grass this weekend and wants to know exactly how much area she will be trimming. Calculate the area of the polygon. Be sure to show all your work and explain your answer.

Answers
Answer:
150 ft²
Step-by-step explanation:
If you take that triangle and place it on the other side you get a normal rectangle and can just multiply 15 By 10
What is a function f of three variables?
Answers
The domain of f is the set of all real numbers f(x,y) as (x,y) varies throughout the domain D with three variables.
What is a function?
A unique kind of relation called a function is one in which each input has precisely one output. In other words, the function produces exactly one value for each input value. The graphic above shows a relation rather than a function because one is mapped to two different values. The relation above would turn into a function, though, if one were instead mapped to a single value. Additionally, output values can be equal to input values.
The functions of a point (or vector) in R2 or R3 that have real values will now be looked at. These functions will typically be defined on sets of points in R2, but there will be occasions when we utilise points in R3 and when it is more convenient to think of the points as vectors (or terminal points of vectors).
Each point f(x,y) in D is given a real number f(x,y) according to a real-valued function f defined on a subset D of R2. The domain of f is the set of all real numbers f(x,y) as (x,y) varies throughout the domain D, and the range of f is the greatest set D in R2 on which f is defined.
Learn more about function, by the following link.
https://brainly.com/question/25638609
#SPJ4
A 2-gallon bucket of paint costs $58.00. What is the price per quart? $
Answers
Answer:
7 dollars and 25 cents
Step-by-step explanation:
there is 8 quarts in 2 gallons then divide 58 dollars by 8 and you get 7 dollars 25 cents
Division is one of the four fundamental arithmetic operations. The price per quart is $7.25 per quart.
What is Division?The division is one of the four fundamental arithmetic operations, which tells us how the numbers are combined to form a new one.
Given that A 2-gallon bucket of paint costs $58.00. Therefore, the price per gallon is,
Price per gallon = $58/2
Since a gallon is equal to 4 quarts. Therefore, the price per quart is,
Price per quart = $58/(4×2) = $7.25 per quart
Learn more about Division:
https://brainly.com/question/369266
#SPJ2
Easy? Please help me
Sarah earns $
8.50
8.50 per hour babysitting. She needs to make at least $
187
187 to buy a new bike.
Write an inequality to represent the number of hours Sarah needs to work to afford the bike.
187
h
≥
8.50
187h≥8.50
187
h
≤
8.50
187h≤8.50
8.50
h
≥
187
8.50h≥187
8.50
h
≤
187
8.50h≤187
Answers
Answer:
The answer is A
Step-by-step explanation:
Hope it helps!
What is the value of x?
K
83°
L
M
(9x + 40)
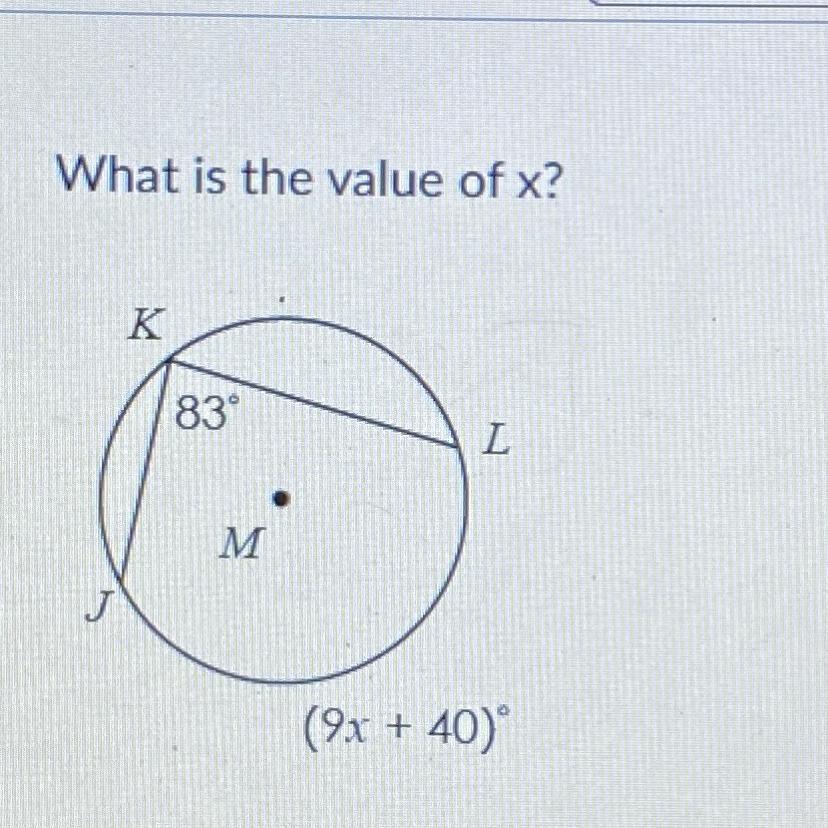
Answers
Answer:
This inscribed angle is half of the intercepted arc JL, so 2(83)= 9x +40.
166 -40 = 9x, x=14.
Step-by-step explanation:
The value of x in the given figure is 14 which we obtain by inscribed angle is half of the intercepted arc.
The inscribed angle is half of the intercepted arc.
83 = 1/2(9x+40)
Now let us find the value for x
83= 9/2x + 20
Subtract 20 from both sides to isolate the x variable
83-20=9/2x
63=9/2x
126=9x
Divide both sides by 9
14 is value of x
x=14
To learn more on Angles click:
https://brainly.com/question/28451077
#SPJ2
Favorite days of the week Monday 55% Tuesday 45% 4) If 220 people were surveyed, how many more people voted for Monday than for Tuesday?

Answers
Answer: 22
Step-by-step explanation:
Ok, so the way I do it I multiply then divide.
For Monday I did: ?/220=55/100. what you would do is multiply across then divide by the other number, so 220x55 which is 12100 then you will divide it by 100. So 121 people voted on Monday
For Tuesday: Using the same method. ?/220=45/100 you will multiply 45x220 giving you 9900 then you will divide by 100 giving you 99. 99 people voted on Tuesday.
So to find the DIFFERENCE you need to subtract, so 121-99 leaving you with 22. Also, if you are confused how on where I got 100 from you put the percentage over 100, because percentages go from 0%-100% so you put the partial percentage over the maximum (100)
A solid shape is made from centimetre cubes.
Here are the plan, side elevation and
Centimetre cubes are added to
front elevation of the shape.
make this cuboid.
Plan Side elevation Front elevation
40
4 cm
3 cm
How many cubes are added?
Write your final answer as,... cubes are added.
Answers
Answer:
30 cubes are added
Step-by-step explanation:
The image of the solid shape is attached.
From the Plan, Side elevation and Front elevation, the number of cubes needed to make the shape is 18 blocks. From the front elevation, 12 blocks is needed (4 * 3 blocks) while from the side elevation 6 blocks are needed given a total of 18 blocks.
The number of blocks needed to make the cuboid = 4 * 4 * 3 = 48 cm cubes.
Therefore the number of cubes to be added = 48 cubes - 18 cubes = 30 cubes.
30 cubes are added

The number of cubes that are added is 30.
What is Cube?
A cube's form is occasionally referred to as "cubic." Another way to put it is that a block with uniform length, width, and height is regarded to be a cube. It also contains 12 edges and 8 vertices, with 3 of the edges coming together at a single vertex point. Examine the illustration below, identifying the faces, edges, and vertices. It is also referred to as a right rhombohedron, an equilateral cuboid, and a square parallelepiped. One of the platonic solids, the cube is a convex polyhedron with all of its faces being square. The cube has either cubical symmetry or octahedral symmetry. The square prism is a specific instance of a cube.
From the Plan, Side elevation, and Front elevation, the number of cubes needed to make the shape is 18 blocks. From the front elevation, 12 blocks are needed (4 * 3 blocks) while from the side elevation 6 blocks are needed given a total of 18 blocks.
The number of blocks needed to make the cuboid
= 4 * 4 * 3 = 48 cm cubes.
Therefore the number of cubes to be added
= 48 cubes - 18 cubes
= 30 cubes.
30 cubes are added.
Hence, The number of cubes that are added is 30.
To learn more about, cubes, visit;
https://brainly.com/question/107100
#SPJ13
The figure consists of a chord, a secant, and a tangent to the circle. The diagram is not drawn to scale.What is the value of x? Round the answer to the nearest unit.

Answers
Answer: 8.46 ✌️
Pythagorean’s theorem
Find the percent of decrease from 49 people to 18 people. Round to the nearest tenth of a percent if necessary.
percent of decrease
%
Answers
49 - 18 = 31
31/49 = 0.63265 x 100
= 63.3 rounded to the nearest tenth of a percent
Consider the relation schema R(A,B,C,D,E) with the following functional dependencies F= {A->B, C->B, D->ABC, AC->D, D->E} Compute the candidate key for the given relation Compute the minimal cover of F.
Answers
The candidate key for the relation schema R(A,B,C,D,E): A→B, C→B, D→A, D→B, D→C, C→D, D→E.
Candidate key for the given relation: To find the candidate key for the relation schema R(A,B,C,D,E), we need to follow the below steps:
Here, we have the following functional dependencies: A→B, C→B, D→ABC, AC→D, D→E.
Step 1: To normalize the given dependencies, we have the following dependencies:
A→B, C→B, D→ABC, AC→D, D→E becomes
A→B, C→B, D→A, D→B, D→C, D→E.
Step 2: To check for the minimal dependency, we can eliminate the redundancy by eliminating D→ABC. Therefore, we have the following dependency:
A→B, C→B, D→A, D→B, D→C, D→E.
Step 3: Find the closure on each attribute, which is as follows:
1. A+ = {A,B}
2. B+ = {B}
3. C+ = {B}
4. D+ = {A,B,C,D,E}
5. E+ = {E}
Step 4: The combination of attributes that have all attributes of the relation schema, and it will be a candidate key is AD. Therefore, the candidate key is AD.
Compute the minimal cover of F:
Minimal Cover: The minimal set of dependencies that is equivalent to the given set of dependencies is the minimal cover.
We have the following functional dependencies:
A→B, C→B, D→ABC, AC→D, D→E.
The process to compute the minimal cover of F is as follows:
Step 1: To find the redundant dependencies, we need to split the dependencies. We have the following dependencies:
A→B, C→B, D→ABC, AC→D, D→E becomes
A→B, C→B, D→A, D→B, D→C, D→E.
Step 2: To eliminate the dependencies with three attributes, we can use the following steps:
If X→YZ, then X→Y and X→Z.
Therefore, we have the following dependency:
D→A, D→B, D→C.
Step 3: To eliminate the dependency with two attributes, we can use the following steps:
If X→Y and Y→Z, then X→Z.
We have the following dependency: AC→D, C→D.
Step 4: Therefore, the minimal cover of F is A→B, C→B, D→A, D→B, D→C, C→D, D→E.
Know more about the dependency
https://brainly.com/question/4294556
#SPJ11
The region between the x-axis and the graph of y=sinx, 0≤x≤π is
revolved about the line x = 2π . Find the volume of the generated
solid. Sketch this solid.
Answers
The given curve is y=sinx. To obtain the volume of the generated solid when the region between the x-axis and the graph of y=sinx is revolved about the line x = 2π, we can utilize the disk method. Consider rotating a point, (x, y), on y=sinx for 0≤x≤π about the line x=2π.
When rotated, we have to notice that a perpendicular line from the rotation axis (x=2π) to the point on the graph will meet the graph on the line y= sinx. Thus, the perpendicular line will have length 2π-x. Also, the function y=sinx, 0≤x≤π represents a wave over a cycle, and its mirror image over x=π. Hence, we can obtain the volume of the generated solid using two symmetric disks. Now let us compute the volume using the disk method. The volume is given by:
∫_0^π〖π(2π-x)^2 sin^2 x dx〗 = 4π^3/3 - 8π^2+ 4π.
The region between the x-axis and the graph of y=sinx, 0≤x≤π is revolved about the line x = 2π to produce a solid. We utilized the disk method to compute the volume of the generated solid. We noted that the curve has two symmetric disks due to its symmetry about x=π. The volume of the generated solid is given by:
∫_0^π〖π(2π-x)^2 sin^2 x dx〗 = 4π^3/3 - 8π^2+ 4π.
The volume of the generated solid is therefore given by:
4π^3/3 - 8π^2+ 4π cubic units.
Therefore, the volume of the generated solid when the region between the x-axis and the graph of y=sinx, 0≤x≤π is revolved about the line x = 2π is 4π^3/3 - 8π^2+ 4π cubic units.
To learn more about disk method visit:
brainly.com/question/31368228
#SPJ11
pat is 17 years older than his son patrick. in 5 years pat will be twice as old as patrick. how old are they now?
Answers
By using linear equation, the patrick is 12 years old and pat is 29 years old.
We take variable x to find out their present age.
What is linear equation?The fundamental equation used to represent and solve for an unknown quantity is a linear equation in one variable. It is always a straight line, and it is simply shown graphically. A mathematical statement is simply represented by a linear equation. Unknown amounts can be symbolised or represented by any variable. There are a few straightforward procedures for solving linear equations. To determine the final value of the unknown quantity, the constants are isolated to one side of the equation and the variables are isolated to the other side.
SolutionLet the age of patrick is 'x'. so the age of his father pat be 'x + 17'.
After 5 years, partrick's age will be 'x + 5'
And his father pat age will be x + 17 + 5 = 'x + 22'
After 5 years pat age will e twice of patrick age.
So that 2(x + 5) = x + 22
⇒ 2x + 10 = x + 22
⇒ 2x - x = 22 - 10
⇒ x = 12
So that the patrick is 12 years old and pat is 29 years old.
To learn ore about linear equation visit:
brainly.com/question/11897796
#SPJ1
Write the linear equation in slope-intercept form passing through the point (0, 3) and that has a slope of 2.
Answers
Answer:
y=2x+3
Step-by-step explanation:
The length of a park is 12 kilometers. What is the length of the park in meters?
Answers
Answer:
12,000
Step-by-step explanation:
There are 1,000 meters in a kilometer. So, if you have 12 kilometers, that's 12,000 meters.
Answer:
12000
Step-by-step explanation:
One kilometer = 100 meters 12 times 1000 = 1200
Tran is making fasnachts (deep-fried German doughnuts) to sell the
Tuesday before Ash Wednesday, her bakery's biggest fasnacht day of
the calendar year. She has 8 pounds of butter and her recipe calls for
1
cup of butter per 2 dozen fasnachts. If 1 pound of butter is 2 cups,
then how many individual fasnacht doughnuts will Tran be able to
make?
Answers
He can make 32 dozen Fasnacht with 8 pounds of butter.
What is the unitary method?The unitary method is a method in which you find the value of a unit and then the value of a required number of units.
Given here, She has 8 pounds of butter and 1 cup of butter can make 2 dozen Fasnacht. Also, 1 pound of butter is 2 cups thus 8 pounds of butter is equivalent to 16 cups.
1 cup of butter to make 2 dozen Fasnacht
then 16 cups of butter can be used to make 16×2=32 dozen Fasnacht
Hence, he can make 32 dozen Fasnacht with 8 pounds of butter.
Learn more about the unitary method here:
https://brainly.com/question/22056199
#SPJ1
Q.5) Helen plays darts. The scores are given below.
(a) Draw an ordered stem and leaf diagram to
show her scores.
(b) Work out the range.

Answers
Answer:
NOT THE ANSWER try to include her scores because there is no data
I need help it’s for math!!

Answers
Answer:
-8, -3, 2 ad 7
Step-by-step explanation:
This graph shown is a polynomial function. The solution is the point where the curves cuts the x axis. From the diagram we can see that the curves cuts the x axis at four points.
The points are at x1 = -8, x2 = -3, x3 = 2 and x4 = 7
Hence the real solutions to the function f(x) = 0 are -8, -3, 2 ad 7
