Answers
Answer:
g
g
g
g
g
g
g
gg
f
ff
f
er
theonlythethe
thethethethe
the
the
thefirst
Ihave
I
I
I have
I
the
II
the
I
the
I
the first
Answer:
16 m
Step-by-step explanation:
Related Questions
24 students in a class took an algebra test. if 18 students passed, what percent passed.
Answers
Answer:
75%
Step-by-step explanation:
18/24=0.75
Answer:
75%
Step-by-step explanation:
24 divided by 4 is 6, so 25% of 24 is 6. 18 divided by 6 is 3, so 18 out of 24 is 75%.
3.[1-4
-4 5-7]
3 -12 15 -21]
[4
-18 -4]
O [3 12 15 21]
O
[4 -12 8 -21]
Answers
Answer:
what is your question because I'm not sure if u accidentally forgot to put the question up
Step-by-step explanation:
Hope I'm able to help you later with your question
find the solution set 8x^2 + 2x-1=0
Answers
Answer:
x= 0.25, -0.5
Step-by-step explanation:
It’s right it think about c
Which statement about the triangles at the right is true? Immersive Reader
(1 Point)
△ABC is similar to △ADF
△ABC is not similar to △ADF
∠BAC is not congruent to ∠DAF
△ABC is congruent to △ADF
Answers
Answer:
I believe the correct answer is B
Step-by-step explanation:
I think you should have a picture of this equation
Answer:
^ABC is not similar to ^ADF
Step-by-step explanation:
I just took this test and i got a A goodluck
fernando competed in an 80 mile bike race. after 0.5 hour, he had ridden 9 miles. after 1 hour of riding, fernando had biked 18 miles. assuming he was traveling at a constant speed, how far will fernando have traveled after 3.5 hours?
Answers
Fernando will have traveled 63 miles after 3.5 hours.
To find the distance Fernando will have traveled after 3.5 hours, we can determine his average speed and then calculate the total distance covered.
We are given that after 0.5 hours, Fernando had ridden 9 miles, and after 1 hour, he had ridden 18 miles. By comparing these two data points, we can see that Fernando is traveling at a constant speed of 18 miles per hour.
To calculate the distance traveled after 3.5 hours, we can multiply the speed (18 miles per hour) by the time (3.5 hours):Distance = Speed × Time = 18 miles/hour × 3.5 hours = 63 miles.
Therefore, Fernando will have traveled 63 miles after 3.5 hours.
It is important to note that this calculation assumes a constant speed throughout the entire race. If the speed varied during the race, the result may be different. However, based on the given information of constant speed, we can conclude that Fernando will have traveled 63 miles after 3.5 hours.
Learn more about average speed here:
brainly.com/question/13318003
#SPJ11
Question 12 of 15
Solve: 8+=(x-4) - 1
A. x = -24
B. There are infinitely many solutions.
C. x = 40
D. x=-40

Answers
the solution of the system of equation where x = -40.
What is a System of Equations?
A system of equations in algebra is made up of two or more equations that are solved together. "A group of equations satisfied by the same set of variables are called a system of linear equations. Finding the values of the variables employed in the system of equations is the first step towards solving it. While maintaining the balance of the equations on both sides, we compute the values of the unknown variables. Finding a variable whose value makes the condition of all the given equations true is the primary goal of solving an equation system.
8+x/2 =1/4(x-4) - 1
⇒8+x/2 = x/4 -1 -1
⇒x/2-x/4 = -10
⇒x/4 = -10
⇒x = -40
Hence the solution of the system of equation where x = -40.
Learn more about System of Equations, by the following link.
https://brainly.com/question/12526075
#SPJ1
What does the complement rule state?
Multiple Choice
\(\ \textless \ br /\ \textgreater \
P(A)=P(A) \times P(B)\ \textless \ br /\ \textgreater \
\)
\(\ \textless \ br /\ \textgreater \
P(A)=P(A)-P(B)\ \textless \ br /\ \textgreater \
\)
\(\ \textless \ br /\ \textgreater \
P(A)=1-P(\mathrm{nos}\space A)\ \textless \ br /\ \textgreater \
\)
\(\ \textless \ br /\ \textgreater \
P(A)=P(A) X-P(B)\ \textless \ br /\ \textgreater \
\)
Answers
The complement rule states that (C) P(A) = 1 - P(A')
The complement rule states that the probability of an event A occurring is equal to 1 minus the probability of the event A not occurring (the complement of A).
Mathematically, the complement rule is represented as:
P(A) = 1 - P(A')
where:
P(A) is the probability of event A,
P(A') is the probability of the complement of event A (not A).
The complement rule is based on the fact that the sum of the probabilities of an event and its complement must equal 1. In other words, if there are only two possible outcomes (A and not A), then the probability of A happening plus the probability of not A happening should equal 1.
By using the complement rule, we can determine the probability of an event indirectly by finding the probability of its complement and subtracting it from 1. This can be useful when calculating probabilities, especially when it is easier to calculate the probability of the complement of an event rather than the event itself.
To know more about complement rule click here :
https://brainly.com/question/29146128
#SPJ4
terms of the series if a=2,b=0.22,c=0.95,k=11.93, and n=3. Round off the final answer to five decimal places.
Answers
The term of the series with n = 3 and the given values is approximately 1532.13607 when rounded to five decimal places.
To calculate the terms of the series with the given values a = 2, b = 0.22, c = 0.95, k = 11.93, and n = 3, we can use the formula for the nth term of the series:
\(T(n) = a * b^(n-1) + c * k^n\)
Substituting the given values, we have:
T(3) = \(2 * 0.22^(3-1) + 0.95 * 11.93^3\)
Simplifying the expression:
T(3) = 2 * 0.22^2 + 0.95 * 11.93^3
T(3) = 2 * 0.0484 + 0.95 * 1612.6729
T(3) = 0.0968 + 1532.0392655
T(3) = 1532.1360655
Rounding off the final answer to five decimal places, we get:
T(3) ≈ 1532.13607
Therefore, the term of the series with n = 3 and the given values is approximately 1532.13607 when rounded to five decimal places.
Learn more about decimal here:
https://brainly.com/question/30958821
#SPJ11
Find each side length.
у
х
45
3
Ox= 3, y = 32
Ox=3V2, y=32
x = 3/2 y=3
x = 3, y = 6/2

Answers
Give in the speeds of each Runner determine who runs the fastest Emily runs 15 ft per second no one runs 358 ft and 36 seconds Liz runs 1 mi in 405 seconds Zack runs 768 feet in 1 minute
Answers
Emily runs at the fastest speed of 15 ft per second, Liz runs at 13.03 ft per second, and Zack runs at 12.8 ft per second.
What is speed?Speed is defined as the ratio of the time distance travelled by the body to the time taken by the body to cover the distance. Speed is the ratio of the distance travelled by time. The unit of speed in miles per hour.
Given that Emily runs 15 ft per second no one runs 358 ft and 36 seconds Liz runs 1 mi in 405 seconds Zack runs 768 feet in 1 minute.
Emily's speed = 15 ft/sec
Liz's speed = 1 mile per 405 sec = 5280/405 = 13.03 ft /sec
Zack's speed = 768 / 60 = 12.8 ft /sec
Therefore, Emily runs at the fastest speed of 15 ft per second, Liz runs at 13.03 ft per second, and Zack runs at 12.8 ft per second.
To know more about Speed follow
brainly.com/question/6504879
#SPJ2
factorise 4px-3my-2pm-6xy
Answers
Answer:
E
Step-by-step explanation:
NO
(0)
Question 2 Consider the dynamic system described by Equation Q2. 85.16400 083.3770 0046.999 ⃗+ 0.079400 00.7030 001.07 ×10⃗+ 0.013600 03.1390 005.124 ×10⃗= 0 0 0 Equation Q2 (a) Calculate the spectral matrix, the undamped natural frequencies and damping ratios of the system in Equation Q2. Identify its fundamental frequency. (b) The following mode shape vectors have been used to diagonalise the equations of motion of the dynamical system presented in Equation Q2: f1 = [0.8076 1.0000 0.8039]T; f2 = [-0.9694 -0.1620 1.0000]T and f3 = [-0.5342 1.0000 -0.3523]T. Calculate the respective matrix of mass normalised mode shapes. (c) Using the mode superposition method, calculate the response of the system for the first physical coordinate y1 assuming the following initial conditions expressed in terms of the modal coordinates: the initial modal displacements are [0 0.5 0]T m and the initial modal velocities are [0 -3 0]T m/s.
Answers
The first physical coordinate y1 can be expressed as y1 = [1 0 0]Y, & The mass-normalised mode shapes can be normalising the mode shape vectors f1, f2, and f3.
Part (a)
In Equation Q2, the spectral matrix, undamped natural frequencies, damping ratios, and fundamental frequency need to be calculated.
The mass matrix is given by [85.16400 083.3770 0046.999; 0.079400 00.7030 001.07 × 10; 0.013600 03.1390 005.124 × 10].
The stiffness matrix is given by [0.16400 00.3770 000.999; 0.079400 00.7030 001.07 × 10; 0.013600 03.1390 005.124 × 10].
The damping matrix is given by [0 0 0; 0 0 0; 0 0 0].The undamped natural frequencies, damping ratios, and fundamental frequency for the system in Equation Q2 can be calculated from the spectral matrix.
The characteristic equation can be written as det(K-mω^2M)=0.where K is the stiffness matrix, M is the mass matrix, ω is the angular frequency, and m is the mass-normalised mode shape.
The roots of this equation are the undamped natural frequencies, and the damping ratios can be calculated from the undamped natural frequencies and mode shapes.
The mass-normalised mode shapes can be calculated by normalising the mode shape vectors f1, f2, and f3.
Part (b)
The mass-normalised mode shapes can be calculated using the mode shape vectors f1, f2, and f3.Part (c)The response of the system for the first physical coordinate y1 can be calculated using the mode superposition method. The initial modal displacements and velocities are given in terms of the modal coordinates.
The response is then calculated using the equation y(t)= Σ ai φi(t), where ai are the modal amplitudes, and φi(t) are the modal shapes given by the mode shape vectors f1, f2, and f3.
The first physical coordinate y1 can be expressed as y1 = [1 0 0]Y, where Y is the vector of physical coordinates. The modal amplitudes can be calculated from the initial modal displacements and velocities.
Learn more about coordinate from the given link
https://brainly.com/question/17206319
#SPJ11
The brightness of the population of 100-watt light bulbs is normal with a mean of 1650 lumens and a standard deviation of 65 lumens. Suppose that 16 light bulbs are randomly selected 1. Explain why the mean brightness of these 16 light bulbs will have a normal distribution 2. Determine the mean and standard deviation of the sampling distribution of the mean brightness of these 16 light bulbs. 3. What is the probability that the mean brightness of the 16 light bulbs is between 1620 lumens and 1640 lumens? 4. Find the 70th percentile for the mean brightness of 16 light bulbs.
Answers
The mean brightness of a random sample of 16 light bulbs from a population of 100-watt light bulbs will have a normal distribution. This is because, according to the Central Limit Theorem, the distribution of sample means from a large sample size (n ≥ 30) drawn from a population with any distribution shape will approximate a normal distribution, regardless of the shape of the original population distribution.
1. The Central Limit Theorem states that the sampling distribution of the mean of a random sample drawn from any population with a finite mean (μ) and a finite standard deviation (σ) will be approximately normally distributed, as long as the sample size is sufficiently large (n ≥ 30). In this case, we have a sample size of 16 light bulbs, which may not be large enough to satisfy the Central Limit Theorem, but since the population is assumed to be normally distributed with known mean (μ = 1650 lumens) and standard deviation (σ = 65 lumens), we can still approximate the sampling distribution of the mean as normal.
2. The mean (μx) of the sampling distribution of the mean brightness of these 16 light bulbs will be the same as the mean of the population (μ = 1650 lumens), since the sample mean is an unbiased estimator of the population mean. The standard deviation (σx) of the sampling distribution of the mean can be calculated using the formula σx = σ / √n, where σ is the population standard deviation and n is the sample size. Plugging in the given values, we get σx = 65 lumens / √16 = 65 lumens / 4 = 16.25 lumens.
3. To find the probability that the mean brightness of the 16 light bulbs is between 1620 lumens and 1640 lumens, we need to calculate the z-scores for these values using the formula z = (x - μx) / σx, where x is the value we are interested in, μx is the mean of the sampling distribution of the mean, and σx is the standard deviation of the sampling distribution of the mean. Plugging in the given values, we get z1 = (1620 - 1650) / 16.25 ≈ -1.85 and z2 = (1640 - 1650) / 16.25 ≈ -0.61. Using a standard normal distribution table or a calculator, we can find the probabilities associated with these z-scores. Let's denote the probability that the mean brightness is between 1620 lumens and 1640 lumens as P(-1.85 < z < -0.61).
The 70th percentile of a normal distribution corresponds to the z-score that separates the lowest 70% of the distribution from the highest 30%. Using a standard normal distribution table or a calculator, we can find the z-score that corresponds to the 70th percentile, denoted as zp70. Then we can use the formula x = μx + zp70 × σx to find the 70th percentile for the mean brightness of 16 light bulbs.
Therefore, The mean brightness of a random sample of 16 light bulbs from a population of 100-watt light bulbs will have a normal distribution due to the Central Limit Theorem, as long as the population is assumed to be normally distributed. The mean of the sampling distribution of the mean will be the same as the mean of the population, which is 1650 lumens.
To learn more about Central Limit Theorem here:
brainly.com/question/18403552#
#SPJ11
hi im spamming the homework questions i got wrong someone help??

Answers
Answer:
55
Step-by-step explanation:
Since angle Arc AC and angle X lies on the same same straight line,
\(angle \: arc \: ac \: + \: angle \: x \: = 180 \\ 125 + x = 180 \\ x = 180 - 125 \\ = 55\)
Answer:
it is 245 because the degrees for circle is 360
Step-by-step explanation:
360-125=245
Find the volume of the solid of revolution generated by revolving about the x-axis the region under the following curve. y= x from x=0 to x=20 (The solid generated is called a paraboloid.) The volume is (Type an exact answer in terms of n.)
Answers
To start, let's sketch the graph of the curve y = x from x = 0 to x = 20. This is simply a diagonal line that passes through the points (0,0) and (20,20), as shown below:
```
|
20 | *
| *
| *
| *
|*
0 --------------
0 10 20
```
Now, we want to revolve this curve around the x-axis to create a solid shape. Specifically, we want to create a paraboloid, which is a three-dimensional shape that looks like an upside-down bowl.
To find the volume of this paraboloid, we need to use calculus. The basic idea is to slice the solid into very thin disks, and then add up the volumes of all the disks to get the total volume.
To do this, we'll use the formula for the volume of a cylinder, which is:
V = πr^2h
where r is the radius of the cylinder and h is its height. In our case, each disk is a cylinder with radius r and height h, where:
- r is equal to the y-value of the curve (i.e. r = y = x), since the disk extends from the x-axis to the curve.
- h is the thickness of the disk, which is a very small change in x. We can call this dx.
So, the volume of each disk is:
dV = πr^2dx
= πx^2dx
To find the total volume of the paraboloid, we need to add up the volumes of all the disks. This is done using an integral:
V = ∫(from x=0 to x=20) dV
= ∫(from x=0 to x=20) πx^2dx
Evaluating this integral gives us:
V = π/3 * 20^3
= 8000π/3
So the exact volume of the paraboloid is 8000π/3.
To know more about paraboloid visit:-
https://brainly.com/question/30634603
#SPJ11
Solve and show your solution on the grid: 2 /3 × 3 /5
Answers
The product of 2/3 and 3/5 is 2/5
Solving fractions on the grid:To represent a fraction on a grid, we need to divide the grid into equal parts based on the denominator of the fraction, and then shade in a number of those parts based on the numerator of the fraction.
Here we have
=> 2/3 × 3/5
To solve 2/3 × 3/5, we multiply the numerators together and the denominators together
=> [ 2/3 × 3/5 ] = 6/15
=> [ 2/3 × 3/5 ] = 2/5
This multiplication can be represented as given in the picture
Therefore,
The product of 2/3 and 3/5 is 2/5
Learn more about Grids at
https://brainly.com/question/30501851
#SPJ1

ECTION B pplication of your knowledge on the nature of roots: Prove that the roots of x² + (1-k)x+k-3=0 are real for all real values of k.
Answers
The roots of the quadratic equation x² + (1-k)x + k-3=0 are real for all real values of k.
Quadratic equation calculation.
The discriminant (D) of the quadratic equation ax² + bx + c = 0 is given by:
D = b² - 4ac
For the given quadratic equation x² + (1-k)x + k-3 = 0, a=1, b=1-k, and c=k-3. Substituting these values into the discriminant formula, we get:
D = (1-k)² - 4(1)(k-3)
D = 1 - 2k + k² - 4k + 12
D = k² - 6k + 13
For the roots of the quadratic equation to be real, the discriminant must be greater than or equal to zero, i.e. D ≥ 0. Therefore, we need to prove that:
k² - 6k + 13 ≥ 0
To find the range of k for which this inequality holds true, we can factor the left-hand side of the inequality as:
k² - 6k + 13 = (k - 3)² + 4
Since the square of any real number is always non-negative, we can see that the left-hand side of the inequality is always greater than or equal to 4, i.e.
(k - 3)² + 4 ≥ 4
Therefore, we have:
k² - 6k + 13 ≥ 0
This inequality holds true for all real values of k. Therefore, the roots of the quadratic equation x² + (1-k)x + k-3=0 are real for all real values of k.
Learn more about quadratic equation below.
https://brainly.com/question/14193054
#SPJ1
Determine the value of x that would make quadrilateral lmno a parallelogram. 3 9 11 18
Answers
The correct answer is x = 9
What is a parallelogram in math?
A parallelogram is a quadrilateral with opposite sides parallel (and therefore opposite angles equal). A quadrilateral with equal sides is called a rhombus, and a parallelogram whose angles are all right angles is called a rectangle.Diagonals of a parallelogram bisect each other.
For quadrilateral LMNO to be a parallelogram, LP must equal PN, and OP must equal PM.
Set OP equal to PM and solve for x.
PM = OP
3x - 9 = 18
Add 9 to both sides.
3x = 27
Divide both sides by 3.
x = 9
Therefore, the value of x = 9
Learn more about parallelogram
brainly.com/question/23857659
#SPJ4
The complete question is -
Determine the value of x that would make quadrilateral LMNO a parallelogram.
3
9
11
18

Answer: x=9
Step-by-step explanation:
solve for x.28+19x=-8+15x
Answers
28+19x=-8+15x
Move the variable terms ( the one with "x" ) to the left side of the equation.
19x-15x = -8-28
4 x = -36
Divide both sides by 4:
4x/4 = -36/4
x= -9
Which of the following measurements must be accurate when used in a grocery store? Check all that apply.

Answers
i am little bit confused
but according to me
C and D must be right
hope this is helpful
What is the slope of the line y =
y = 1/x+4?
OA. 4
O B. -1/2
O C. 1/2
OD. -4
Answers
Answer:
The equation y = 1/(x+4) can be rewritten in slope-intercept form (y = mx + b) by isolating y:
y = 1/(x+4) can be rewritten as y = (1/x)/(1/4) = 4/x
So the equation y = 4/x is in slope-intercept form, where the slope is the coefficient of x, which is 4.
Therefore, the slope of the line y = 1/(x+4) is 4, and the correct answer is (A) 4.
a. find the probability that there will be no accidents during the month at the factory. b. find the probability that there will be 4 or more accidents during the month at the factory. c. given that the factory had at least one accident during the month, find the probability that the factory had 4 or more accidents during the month.
Answers
To find the probability for no accidents use the formula P(no accidents) = (1-p)^n, To find the probability that there will be 4 or more accidents use the formula P(4 or more accidents) = 1 - P(0, 1, 2, 3 accidents), and at least one accident during the month, t - use the formula P(4 or more accidents) = 1 - P(0, 1, 2, 3 accidents).
a. To find the probability that there will be no accidents during the month at the factory, use the formula P(no accidents) = (1-p)^n, where p is the probability of an accident occurring and n is the number of trials (in this case, the number of days in the month).
b. To find the probability that there will be 4 or more accidents during the month at the factory, use the formula P(4 or more accidents) = 1 - P(0, 1, 2, 3 accidents), where P(0, 1, 2, 3 accidents) is the probability of 0, 1, 2, or 3 accidents occurring during the month.
c. Given that the factory had at least one accident during the month, the probability that the factory had 4 or more accidents during the month is the same as in part b - use the formula P(4 or more accidents) = 1 - P(0, 1, 2, 3 accidents).
To know more about probability refer to-
brainly.com/question/30034780#
#SPJ11
Which of the following is not a possible answer to a probability question?
00
0 1.2%
O 120
O 2/3
Answers
Answer:
which of the following is not a possible answer to a probability question 2 by 3 that is not a probability questions answer because always a probability will come in the probability of an event ok so 232 want to come
how do you solve 2x²+4x=3+3x²
Answers
First get everything on one side
0= x^2 -4x + 3
Here to solve x you could do a few methods like quadratic equation. But a simpler way is to factor it out.
(x-3)(x-1)
Equal both of those to zero to find what x can be.
So the answers would be 3 and 1
one end of a 10-foot ladder is 6 feet from the base of a wall. how high on the wall does the top of the ladder touch?
Answers
The top of the ladder touches a height of 8 feet on the wall. To determine how high on the wall the top of the ladder touches, we can use the Pythagorean theorem.
In this case, the ladder forms the hypotenuse of a right triangle, and the base of the wall and the height on the wall form the other two sides.
Let's denote the height on the wall as 'h'. According to the problem, one end of the ladder is 6 feet from the base of the wall, so the base of the triangle is 6 feet.
We can set up the equation using the Pythagorean theorem:
\((6)^2 + (h)^2 = (10)^2\)
Simplifying the equation:
36 + \(h^2\) = 100
\(h^2\) = 100 - 36
\(h^2\)= 64
Taking the square root of both sides:
h = √64
h = 8
Therefore, the top of the ladder touches a height of 8 feet on the wall.
Learn more about Pythagorean theorem here:
https://brainly.com/question/14930619
#SPJ11
c. probability that the mother in this sample had a premature baby given that the mother admitted to smoking
Answers
Probability that the mother in this sample had a premature baby given that the mother admitted to smoking is 50 percent.
What is probability?Likelihood is the part of science concerning mathematical depictions of how likely an occasion is to happen, or how likely it is that a suggestion is valid. The likelihood of an occasion is a number somewhere in the range of 0 and 1, where, generally talking, 0 demonstrates difficulty of the occasion and 1 shows conviction.
P (A) is the probability of an event “A”
n (A) is the number of favorable outcomes
n (S) is the total number of events in the sample space
The higher the likelihood of an occasion, the more probable it is that the occasion will happen. A straightforward model is the throwing of a fair coin. Since the coin is fair, the two results are both similarly likely; the likelihood of "heads" approaches the likelihood of "tails"; and since no different results are conceivable, the likelihood of by the same token "heads" or "tails" is 1/2.
To learn more about probability, visit:
https://brainly.com/question/28215213
#SPJ4
Which questions must be considered when evaluating the effectiveness of an argument? select four options.
Answers
The questions that must be considered when evaluating the effectiveness of an argument are:
Is there reliable evidence to support the reasons?Are there logical reasons to believe the claim?Is the author's claim clear to the reader?Does the author's diction affect the reader as intended?What is an Argument?This is referred to a statement which determines the truth or acceptability of another called conclusion.
To evaluate the effectiveness of an argument features such as logicality, diction etc must be considered.
Read more about Argument here https://brainly.com/question/3775579
#SPJ1
find the measure of arc AC

Answers
Answer:
Step-by-step explanation:
Angle ABC is an inscribed angle intercepting arc AC. The rule is that the intercepted arc is twice the measure of the angle that intercepts it, so arc AC = 2(65) which is 130
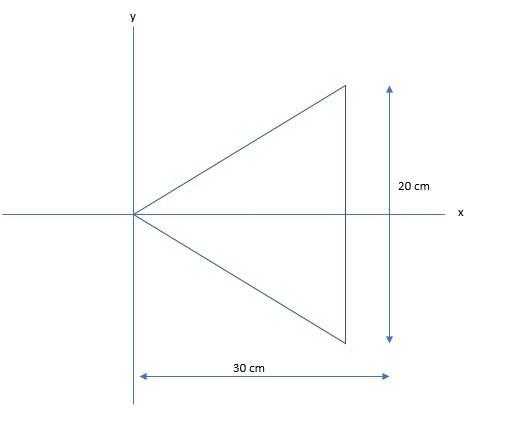
an 800 g steel plate has the shape of the isosceles triangle shown in the figure(figure 1).
Answers
The x- and y-coordinates of the center of mass are; (20, 0)
What is the center of mass of an object?The center of mass is the location where the sum of the relative position of the masses in a mass distribution is zero. It is the point where force can be applied on the distributed mass without causing a rotation of the system.
The mas of the steel plate = 800 g = 0.8 kg
The base length of the isosceles triangular plate = 20 cm = 0.2 m
The height of the isosceles triangular plate = 30 cm = 0.3 m
Considering a small strip of height, dx and width, I, we get
Area of small strip, dA = I·dx
Density of the plate for a unit thickness, ρ = M/A
Density of the small strip of mass dm = dm/dA
Considering the density of the plate as uniform, we get;
\(\displaystyle {\frac{dm}{dA} =\frac{M}{A}\)
Therefore;
\(\displaystyle {dm=\frac{M}{A}\times dA}\)
The area of the triangular plate, A = (1/2) × 0.2 m × 0.3 m = 0.03 m²
Mass of the plate, M = 0.8 kg
Therefore;
\(\displaystyle {dm=\frac{0.8}{0.03}\times I\cdot dx}\)
The width of the small strip, I, located at a distance x from the vertex of the triangular plate, using similar triangles, indicates;
\(\dfrac{I}{20} = \dfrac{x}{30}\)
\(I=20\times \dfrac{x}{30} = \dfrac{2}{3} \cdot x\)
Therefore;
\(\displaystyle {dm=\frac{0.8}{0.03}\times I\cdot dx} = \frac{0.8}{0.03}\times \dfrac{2}{3} \cdot x\cdot dx}\)
The center of mass, \(x_{cm}\), can be obtained with the formula; \(\displaystyle {x_{cm} = \dfrac{1}{M} \cdot \int\limits {x} \, dm }\)
Therefore; \(\displaystyle {x_{cm} = \dfrac{1}{0.8} \cdot \int\limits {x} \cdot \frac{0.8}{0.03} \cdot \frac{2}{3}\cdot x\, dx }\)
\(\displaystyle {x_{cm} = \dfrac{1}{0.8} \cdot \int\limits {x} \cdot \frac{0.8}{0.03} \cdot \frac{2}{3}\cdot x\, dx } = \dfrac{1}{0.8} \times \frac{0.8}{0.03} \times \frac{2}{3}\cdot \int\limits^3_0 {x^2} \, dx\)
\(\displaystyle {x_{cm} = \dfrac{1}{0.8} \times \frac{0.8}{0.03} \times \frac{2}{3}\cdot \int\limits^3_0 {x^2} \, dx = \frac{200}{9} \cdot \left[\frac{x^3}{3} \right]^{0.3}_0\)
\(\displaystyle {x_{cm} = \frac{200}{9} \cdot \left[\frac{x^3}{3} \right]^{0.3}_0=\frac{200}{9} \times \frac{0.027}{3} =0.2\)
The location of the x-coordinate center of mass, \(x_{cm}\) = 0.2 m = 20 cm from the vertex, which is the same location as the x-coordinate of the centroid of the plate of uniform density.
The plate is symmetrical about the x-axis, therefore, the y-coordinate of the center of mass is along the x-axis, which is \(y_{cm}\) = 0
The coordinate of the center of mass = (0.2, 0)
Part of the question requires the location of the coordinate of the center of mass of the triangular plate
Learn more about the center of mass of regular shapes here:
https://brainly.com/question/28021242
#SPJ1

B = 18, c = 30 a = ?
