If you reflect FGH across the x-axis, what will be the coordinates of the vertices of the image F’G'H'?

Answers
Answer:
F ' = (-2, 1)
G ' = (2, -2)
H ' = (4, 3)
========================================
Explanation:
The rule \((\text{x},\text{y})\to (\text{x},-\text{y})\) reflects any point over the x axis.
We keep the x coordinate the same. The y coordinate flips from positive to negative, or vice versa.
For example, let's use that rule on point F.
\((\text{x},\text{y})\to (\text{x},-\text{y})\\\\(-2,-1)\to (-2,-(-1))\\\\(-2,-1)\to (-2,1)\\\\\)
Therefore, point F ' is located at (-2,1).
Follow that same logic for points G and H.
Let me know if you need to see the steps for the other points.
Related Questions
Decide whether the normal sampling distribution can be used. If it can be used, test the claim about the population proportion p at the given level of significance a using the given sample statistics. Claim: p 0.11 ; α-0.05: Sample statistics: p-0.08, n-25 Can the normal sampling distribution be used? OA. No, because np is less than 5. OB. Yes, because both np and nq are greater than or equal to 5 ° C. Yes, because pq is greater than -0.05. D. No, because nq is less than 5
Answers
The normal sampling distribution cannot be used, according to the given sample statistics and claim about the population proportion. The correct answer is option A, "No, because np is less than 5."
To determine whether the normal sampling distribution can be used to test the given claim about the population proportion, we need to check whether the conditions for a normal approximation are met. There are three conditions that need to be satisfied:
The sample size should be large enough (n ≥ 30). However, in this case, the sample size is only 25, which is not large enough.
The expected number of successes (np) and the expected number of failures (nq) should both be greater than or equal to 5. In this case, np = (25)(0.11) = 2.75 and nq = (25)(0.89) = 22.25, so np is less than 5.
The sample is independent and random. There is no information given in the question to suggest that this condition is not met.
Therefore, the correct answer is option A, "No, because np is less than 5." Since np is less than 5, we cannot use the normal sampling distribution to test the claim about the population proportion p at the given level of significance α = 0.05 using the given sample statistics p = 0.08 and n = 25. Instead, we would need to use the binomial distribution to calculate the probability of obtaining a sample proportion of 0.08 or less assuming the null hypothesis is true.
To learn more about sampling distribution here:
brainly.com/question/29375938#
#SPJ11
Look at the graph. All of the following statements are true except

Answers
Answer:
The incorrect statement is decreasing from (-∞, -1)
Step-by-step explanation:
Intercepts are where it touches the axis
The x intercepts are -2 and 1
Increasing is where it goes up
We are increasing from (-∞, -1) and (1,∞)
Decreasing is where it goes down
We are decreasing from ( -1,1)
The incorrect statement is decreasing from (-∞, -1)
Leticia spends $18.45 on a shirt. She spends at least $3.00 more than Humberto spends. If h represents the amount Humberto spends, which symbol can be used to complete the inequality below to represent this situation?
18.45 blank 3 + h
>
<
Greater-than-or-equal-to
Less-than-or-equal-to
Answers
Answer:
>
Step-by-step explanation:
28.45 >3+hgydnjsjsjjsjkso
(2/5)^-2(-3)^4
What is the equivalent?
Answers
Answer:
-8100
Step-by-step explanation:
(2/5)^-2(-3)^4
Given data
and second term
The first term= (2/5)^-2 and
Second term=(-3)^4
Simplify the first term
(2/5)^-2= 2^-2/ 5^-2= 1/2^2 * 1/5^2
=1/4/ 1/25
=1/4*25/1
=100
Simplify the second term
=(-3)^4
= -81
Hence, 100*81
=-8100
I’m confused on this type of math

Answers
Answer:
all you do is add
Step-by-step explanation:
let g be the function defined by g(x)=∫x−1(−12 cos(t 3 2t))ⅆt for 0
Answers
Let g be the integral function defined by g(x) = ∫x-1 (-1/2 * cos (t³ / 2t)) dt for x = 0, g is g(x) = -1/2(x-1 * sin(t³/2t) - x-1 * cos(t³/2t)).
To solve this integral, we need to use the substitution method. We will let u = t/2t, du = 3t/2 dt.
Thus, the integral becomes:
g(x) = -1/2 * ∫x-1 cos(u) du
Using integration by parts, we get:
g(x) = -1/2(x-1 * sin(u) + ∫x-1 sin(u) du).
After integrating the second part, we obtain the final result:
g(x) = -1/2(x-1 * sin(u) - x-1 * cos(u))./2t
we subtitute the value of u to get:
g(x) = -1/2(x-1 * sin(t³/2t) - x-1 * cos(t³/2t)).
Learn more about Integral here: brainly.com/question/18125359
#SPJ11
For a criminal trial, 8 active and 4 alternate jurors are selected. Two of the alternate jurors are male and two are female. During the trial, two of the active jurors are dismissed. The judge decides to randomly select two replacement jurors from the 4 available alternates. What is the probability that both jurors selected are female? 1/12 1/6 1/2 1/4
Answers
The probability that both jurors selected are female is 1/6. To calculate the probability that both jurors selected are female,.
We need to determine the number of favorable outcomes (two female jurors selected) divided by the total number of possible outcomes.
In this scenario, there are two female alternate jurors available out of a total of four alternates. Since we need to select two jurors, we can use combinations to calculate the number of possible outcomes.
The number of possible outcomes is given by selecting 2 jurors out of 4, which can be calculated as:
C(4, 2) = 4! / (2! * (4-2)!) = 6
Therefore, there are 6 possible outcomes.
Out of these possible outcomes, we are interested in the favorable outcome where both selected jurors are female. Since there are two female alternate jurors available, we can calculate the number of favorable outcomes by selecting 2 female jurors out of 2, which is:
C(2, 2) = 2! / (2! * (2-2)!) = 1
Therefore, there is 1 favorable outcome.
Now, we can calculate the probability:
Probability = Number of favorable outcomes / Number of possible outcomes
= 1 / 6
= 1/6
Thus, the probability that both jurors selected are female is 1/6.
Learn more about probability here:
https://brainly.com/question/32117953
#SPJ11
simplify/solve the follow equationslogA1logAAlog A x Blog (a/b)log A ^ Blog 1/A
Answers
Using the logarithm quotient rule, it can be simplified to log1 - logA. Since log1 = 0 for any base, this simplifies further to -logA.
We simplify and solve the given expressions using the mentioned terms. Here are the step-by-step explanations for each expression:
1. logA: This expression represents the logarithm of a number A to a specified base. Without any base provided, it cannot be simplified further.
2. 1logAA: Since the coefficient of the logarithm is 1, this simplifies to logAA, which represents the logarithm of A to the base A. By definition, logAA = 1.
3. logA x Blog (a/b): This expression seems to have formatting issues, so I'll break it down into two separate expressions: - logA x B: This represents the logarithm of the product AB to a specified base. Using the logarithm product rule, it can be simplified to logA + logB. - log (a/b): This represents the logarithm of the quotient a/b to a specified base. Using the logarithm quotient rule, it can be simplified to loga - logb.
4. log A ^ B: This expression represents the logarithm of A raised to the power of B to a specified base. Using the logarithm power rule, it can be simplified to B * logA. 5. log 1/A: This expression represents the logarithm of the reciprocal of A (1/A) to a specified base.
Using the logarithm quotient rule, it can be simplified to log1 - logA. Since log1 = 0 for any base, this simplifies further to -logA.
Learn more about logarithm product rule,
https://brainly.com/question/30133428
#SPJ11
Rename 2/1 using the least common denominator, 4.
Answers
Answer:
8/4
Step-by-step explanation:
2/1
We want a denominator of 4 so multiply by 4/4
2/1 * 4/4 = 8/4
2 + 2 x 5 x 10 =
I need help please!
Answers
Answer:
102
Step-by-step explanation:
50×2+2
100+2
give brilliant answer
\(2+2 \times 5 \times 10 \\ =2+(10)(10) \\ =2+100 \\ =102 \\ \)
reglas de la potenciacion
Answers
Identify the vertex of this absolute value function: f(x) = -2|x + 1| + 2. Type the correct answer in each box. Use numerals instead of words.
Answers
Answer:
Step-by-step explanation:
x+1=0
then f(x)=2
x=-1
vertex is (-1,2)
Answer:
-1,2
Step-by-step explanation:
Plato
Anita needs to buy 7 1/2 feet of packaging tape. There are 1 1/2 feet of tape on each roll. How
many rolls of tape should Anita buy?
Answers
Answer:
5
Step-by-step explanation:
you don't have to but i convert 7 1/2 and 1 1/2 into 7.5 and 1.5 to make it easier than you divide.
how many food calories (in kcal) would a well-conditioned athlete metabolize in doing the same work with an efficiency of 25%? (enter a number.)
Answers
201 food calories (kcal) would be sufficient for a well-conditioned athlete to metabolize in doing the same work with an efficiency of 25%
Assuming input the 25% into equation and work
with the help of the equation, we know:
η = work_out / work_in
therefore we get, 0.25 = (2.10e5) / (kcal)
then, kcal = (2.10e5J)/(0.25)
kcal = 2.10e5 J / 0.25
upon dividing the following we get the answer,
kcal = 840e3J
now we need to convert the Joules to kcal and we get,
we know that, 1kcl = 4184J
therefore, 840e3 / 4184 = 201 kcal
hence we know that 201 food calories (kcal) would be sufficient for a well-conditioned athlete to metabolize in doing the same work with an efficiency of 25%
To learn more about kcal and joules, click here:
brainly.com/question/1261409
#SPJ4
Find the indefinite integral \( \int x^{2} \ln x d x \)
Answers
Integrating the second term on the right-hand side gives (-\frac{x^3}{9} + C), where (C) is the constant of integration. Thus, the final answer is:
[\int x^{2}\ln x dx = \frac{1}{3}x^3\ln x - \frac{x^3}{9} + C]
To find the indefinite integral (\int x^{2} \ln x dx), we can use integration by parts with (u = \ln x) and (dv = x^{2}dx), which gives us:
[\int x^{2}\ln x dx = \frac{1}{3}x^3\ln x - \int\frac{x^2}{3} dx]
Integrating the second term on the right-hand side gives (-\frac{x^3}{9} + C), where (C) is the constant of integration. Thus, the final answer is:
[\int x^{2}\ln x dx = \frac{1}{3}x^3\ln x - \frac{x^3}{9} + C]
The process used to find the indefinite integral (\int x^{2}\ln x dx) is known as integration by parts. This method involves selecting two functions, u and dv, such that their product can be written in a way that makes it easier to integrate. In this case, we choose u = ln x because its derivative is simple, and dv = x^2 dx because it is easy to integrate.
Using the formula for integration by parts, we obtain:
[\int x^2 \ln x dx = \int u dv = u v - \int v du,]
where (v) is the antiderivative of (dv), and (du) is the derivative of (u).
We compute the antiderivative of (v) as follows:
[v = \int x^{2} dx = \frac{x^{3}}{3}]
Next, we compute the derivative of (u) as follows:
[du = \frac{d}{dx}(\ln x) dx = \frac{1}{x} dx]
Substituting these values into the integration by parts formula yields:
[\int x^{2}\ln x dx = \frac{x^{3}}{3} \ln x - \int \frac{x^{3}}{3} \cdot \frac{1}{x} dx]
Simplifying the expression gives us:
[\int x^{2}\ln x dx = \frac{x^{3}}{3} \ln x - \frac{1}{3} \int x^{2} dx]
Integrating the second term on the right-hand side gives us:
[-\frac{x^{3}}{9} + C]
where (C) is the constant of integration. Therefore, the final answer is:
[\int x^{2}\ln x dx = \frac{1}{3}x^{3}\ln x - \frac{x^{3}}{9} + C]
This is the indefinite integral of (x^{2} \ln x) that we wanted to find.
Learn more about integration from
https://brainly.com/question/31440081
#SPJ11
the first step in developing a competency model is:
Answers
The first step in developing a competency-model is to gather background information and analyze the existing standards within the workplace.
The first-step involves conducting a thorough examination of the organization's goals, strategies, and the specific job roles or positions for which the competency-model will be developed.
By gathering background information, organizations can understand the context in which the competency-model will be applied.
Analyzing existing standards within the workplace involves assessing the current performance expectations, competencies, and criteria used for evaluating employees in their respective roles.
The purpose of this step is to identify any gaps or areas for improvement in the existing standards and to ensure that the development of the competency model aligns with the organization's overall objectives.
Learn more about Competency Model here
https://brainly.com/question/10857463
#SPJ4
The first step in developing a competency model is conducting a job analysis.
developing a competency model is a systematic process that helps organizations define the key competencies needed for their employees. The first step in this process is conducting a job analysis.
A job analysis involves gathering information about the job, such as its purpose, tasks, responsibilities, and required qualifications. This information can be collected through methods like interviews, observations, and surveys. By analyzing the job, organizations can identify the critical competencies that are necessary for effective job performance.
These competencies can then be used to guide various HR processes, including recruitment, selection, training, and performance management. By aligning the competencies with job requirements, organizations can ensure that they have the right people with the right skills in the right positions.
Learn more:About developing a competency model here:
https://brainly.com/question/10567895
#SPJ11
Which of the following is equal to the opposite of -45?
O-(-45)
O-45
O-1-451
O-145!
Answers
Step-by-step explanation:
A o option
-(-45)
hope it helps
Use Trigonometric substitution to eliminate the roots 1.1. 164+2 + 1 Use Trigonometric substitution to eliminate the roots 1.1. V64+2 + 1 1.2. V4z2 – 49
Answers
To eliminate the roots in 1.1 and 1.2, we can use trigonometric substitution. In 1.1, we can substitute x = 4 sin(theta) to eliminate the root of 4. In 1.2, we can substitute z = 7 sin(theta) to eliminate the root of 7.
1.1. V64+2 + 1 We can substitute x = 4 sin(theta) to eliminate the root of 4. This gives us:
V64+2 + 1 = V(16 sin^2(theta) + 2 + 1) = V16 sin^2(theta) + V3 = 4 sin(theta) V3 1.2. V4z2 – 49
We can substitute z = 7 sin(theta) to eliminate the root of 7. This gives us:
V4z2 – 49 = V4(7 sin^2(theta)) – 49 = V28 sin^2(theta) – 49 = 7 sin(theta) V4 – 7 = 7 sin(theta) (2 – 1) = 7 sin(theta)
Here is a more detailed explanation of the substitution:
In 1.1, we know that the root of 4 is 2. We can substitute x = 4 sin(theta) to eliminate this root. This is because sin(theta) can take on any value between -1 and 1, including 2.
When we substitute x = 4 sin(theta), the expression becomes V64+2 + 1 = V(16 sin^2(theta) + 2 + 1) = V16 sin^2(theta) + V3 = 4 sin(theta) V3
In 1.2, we know that the root of 7 is 7/4. We can substitute z = 7 sin(theta) to eliminate this root. This is because sin(theta) can take on any value between -1 and 1, including 7/4.
When we substitute z = 7 sin(theta), the expression becomes: V4z2 – 49 = V4(7 sin^2(theta)) – 49 = V28 sin^2(theta) – 49 = 7 sin(theta) V4 – 7 = 7 sin(theta)
To know more about root click here
brainly.com/question/16880173
#SPJ11
I need anyone to plz answer this very soon

Answers
Answer:
29°
Step-by-step explanation:
\(In\: \triangle CDE\\\\
m\angle C + m\angle D + m\angle E = 180\degree \\\\
48\degree + 74\degree + m\angle E = 180\degree \\\\
122\degree + m\angle E = 180\degree \\\\
m\angle E = 180\degree- 122\degree \\\\
\huge \red {m\angle E = 58\degree} \\\\
\because \triangle ABC \cong \triangle DEC... (given) \\\\
\therefore \angle B \cong \angle E.. (CACT) \\\\
\therefore m\angle B = m\angle E\\\\
\therefore 2x = 58\degree \\\\
\therefore x =\frac{58\degree}{2}\\\\
\huge \orange {\boxed {\therefore x = 29\degree}}
\)
What is the equation of the line that passes through the point (−4, 8)
and has a slope of zero?
Answers
Answer:
y=8
Step-by-step explanation:
Slope-intercept form
y=mx+b
Plug in values
y=0x+b
8=0(-4)+b
b=8
substitute
y=8
Micheal swam 82 laps in his pool in the morning and 64 laps in his pool in the evening. About how many more laps did he swim in the morning than he did in the evening?
Answers
Michael swam about 18 more laps in the morning than he did in the evening.
The operation or process of finding the difference between two numbers or quantities is known as subtraction. To subtract a number from another number is also referred to as 'taking away one number from another'.
To find out how many more laps Michael swam in the morning than in the evening, we can subtract the number of laps he swam in the evening from the number of laps he swam in the morning.
Morning laps: 82 laps
Evening laps: 64 laps
To find the difference, we subtract:
82 laps - 64 laps = 18 laps
Know more about subtract here:
https://brainly.com/question/2346316
#SPJ11
What is the yield to maturity on a 1000 face value discount bond maturing in one year that sells for $800?
Answers
Since the bond is a discount bond, it's only payment is the repayment of the par value at maturity, i.e., in one year.Yield to maturity = 25%
Yield to maturity (YTM) is the total rate of return a bond will have achieved after all interest payments and principal repayments have been made.
In essence, YTM represents the internal rate of return (IRR) on a bond if held to maturity.It can be difficult to calculate yield to maturity because it makes the assumption that the bond's rate of return is applicable to all interest and coupon payments.
800 = \(\frac{1000} {1 + \:\:yield \:\:to \:maturity}\)
1 + Yield to maturity = 1.25
Yield to maturity = 25%
Learn more about Yield to maturity
brainly.com/question/26376004
#SPJ4
If m7 is 100 find m3
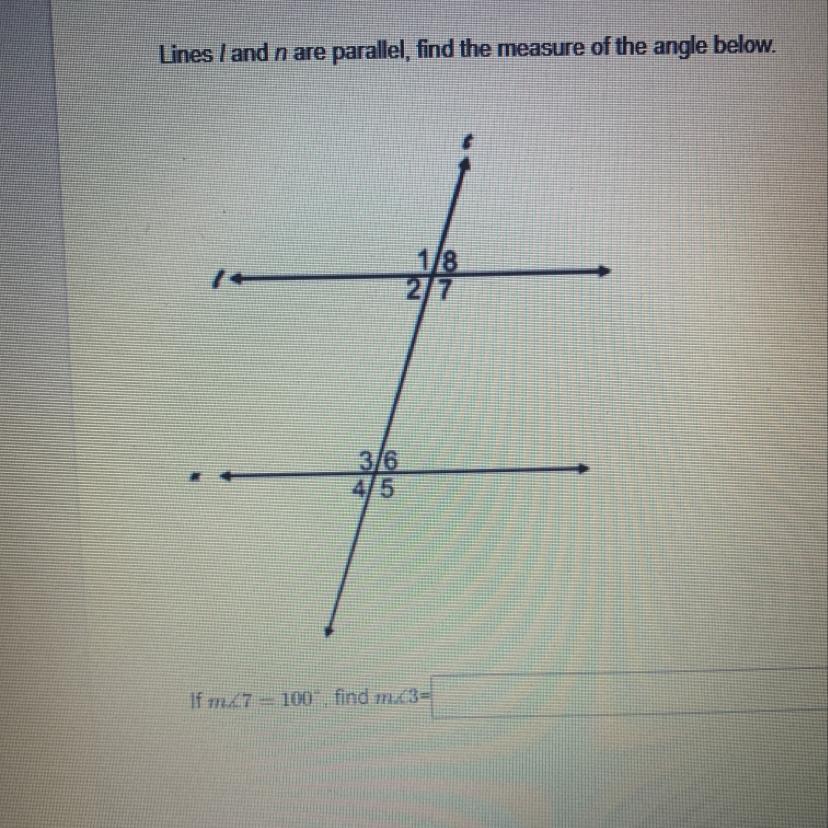
Answers
Answer:
m3 is 100 degrees
Step-by-step explanation:
In this case, angle 7 is congruent to angle 5 because both their angles are located on the same place in different lines. Another rule you need to know is that angles across from each other are equal. So, if angle 5 is 100 degrees, then angle 3 is also 100 degrees because they are across from each other.
hi please help i’ll give brainliest

Answers
Answer:
The answer is 28y + 63
Step-by-step explanation:
7(4y+9)
=28y+63
f(x) = k for 108 < x < 148 what value of k makes f(x) a valid pdf? answer to three decimal places.
Answers
The value of k that makes f(x) a valid pdf is approximately 0.025 to three decimal places.
To make f(x) a valid probability density function (pdf), we need to ensure that the area under the curve between 108 and 148 equals 1. We can use the formula for the area of a rectangle to find the value of k that satisfies this condition.
The width of the rectangle is 148 - 108 = 40, and the height of the rectangle is k. Therefore, the area of the rectangle is 40k.
For f(x) to be a valid pdf, the area under the curve must equal 1. That is:
∫108^148 f(x) dx = 1
Using the formula for a rectangular area, we know that:
∫108^148 f(x) dx = 40k
Therefore, we need to solve the equation:
40k = 1
k = 1/40
So the value of k that makes f(x) a valid pdf is 0.025 (rounded to three decimal places).
To ensure that f(x) is a valid probability density function (pdf), the area under the curve between the specified limits (108 < x < 148) must be equal to 1. Since f(x) = k is a constant function, the area under the curve can be calculated as the product of k and the width of the interval (148 - 108).
Area = k × (148 - 108)
1 = k × 40
To find the value of k, we can solve the equation:
k = 1 / 40
k ≈ 0.025
Thus, the value of k that makes f(x) a valid pdf is approximately 0.025 to three decimal places.
To know more about probability density function visit:
https://brainly.com/question/31039386
#SPJ11
In general, which of the following could be an appropriate null hypothesis? selection was . selection was . selection was . selection was . selection was . selection was .
Answers
In general, an appropriate null hypothesis is one that states there is no significant difference or relationship between two variables.
Therefore, out of the options given, the appropriate null hypothesis would be "selection was not a significant factor."
An appropriate null hypothesis is "Selection has no effect on the observed outcome. "it means that any differences observed in the data are due to chance, and not due to a specific selection process or factor. The null hypothesis serves as a starting point in statistical analysis, and researchers aim to either accept or reject it based on the evidence collected.
Visit here to learn more about statistical analysis:
brainly.com/question/30591800
#SPJ11
This shows the net of a triangular prism.
What is the surface area of the prism?
3,900 m2
4,200 m2
4,800 m2
12,000 m2

Answers
Step-by-step explanation:
Two rectangles 2 x 25 x 40
one rectangle 40 x 40
two triangles (Area = 1/2 * base * height)
2 x 1/2 * 40 * 15
Total = 4200 m^2
4. A prism has an area of cross-section of 89 cm². The volume of the prism is
4895 cm?. Find the height of the prism.
Answers
Answer:
55 cm
Step-by-step explanation:
height = 4895/89 = 55 cm
pls, help I will make you the branliest!

Answers
Answer:
See below
Step-by-step explanation:
Use protractor to measure the UNmarked angle (approx 135 degrees)
then subtract this value from 360 degrees to find the angle in question
what is the solution set of |-x+4|=-3
Answers
The equation | -x + 4 | = -3 does not have a solution set.
The absolute value of a number is always non-negative, meaning it is either zero or positive. The absolute value of any expression, including -x + 4, cannot be negative. However, in this equation, the right side is -3, which is negative. The equation | -x + 4 | = -3 does not have a solution in the set of real numbers.
The absolute value of a number is always non-negative, meaning it is either zero or positive. The absolute value of any expression, including -x + 4, cannot be negative. However, in this equation, the right side is -3, which is negative.
Since the absolute value cannot be negative, there are no values of x that can satisfy the equation | -x + 4 | = -3. Therefore, the solution set is indeed empty or "no solution" in the set of real numbers.
To know more about solution set,
https://brainly.com/question/11988499
#SPJ11