If you have a job and you make $36,000 a year and 42% of it goes to taxes and deductions then how much in dollars are you paying in taxes?
Answers
Answer:
$36,042
Step-by-step explanation:
If you add 36,000 and 42 it will give you that answer
because it is telling you how much are you paying in taxes
Related Questions
HELP ME
Final exam guide due
Show work

Answers
The approximate height of the tree is given as follows:
45.6 ft.
What is the geometric mean theorem?The geometric mean theorem states that the length of the altitude drawn from the right angle of a triangle to its hypotenuse is equal to the geometric mean of the lengths of the segments formed on the hypotenuse.
The altitude segment for this problem is given as follows:
14.5 ft.
The bases are given as follows:
5.2 ft and x ft.
Hence the value of x is given as follows:
5.2x = 14.5²
x = 14.5²/5.2
x = 40.4 ft.
Hence the height of the three is given as follows:
5.2 + 40.4 = 45.6 ft.
More can be learned about the geometric mean theorem at brainly.com/question/10216660
#SPJ1
Alex mows lawns. He earns $15 per lawn. How much does he earn in 4 days if he mows 5 lawns per day?
Answers
Answer:
He would make 300 dollars.
Step-by-step explanation:
15 x 5 = 75
75 x 4 = 300.
Answer:
answer is 300
Step-by-step explanation:
Because if your doing it for 1 day you would have to 15*5 which five you 75. Then you multiple that 75 with the 4 and give you 300 within the 4 days..
Hopes this help.
Which choice is equivalent to the quotient below?

Answers
Answer: B. 4
Which algebraic expression is equivalent to the expression below?
6(5x - 9) + 10x
A. 20x - 54
B. 40x-54
C. 20x + 54
D40X-9
Answers
Answer
D
Step-by-step explanation:
How many 2/3 cup servings are there in a container that holds 7 cups?
Answers
Answer:
10.5
Step-by-step explanation:
A farmer earns $___ for each orange she sells. She had to pay $___ for fertilizer. Part A: Rewrite the description by filling in the blanks with values of your choice to show the amount of money the farmer could earn selling any number of oranges, n. Make sure the values you choose make sense for this situation. (6 points) Part B: Write an algebraic expression from your written description used in Part A. Let n stand for the number of oranges. (6 points)
Answers
Part B: The algebraic expression for the amount of money the farmer could earn selling any number of oranges, n, is 0.20n - 25.
What does the graph of f(x)=(x-3)^2+12 look like
Answers
Answer:
see attached for a graph
Step-by-step explanation:
When g(x) is transformed to
f(x) = f(x -h) +k
The graph of g(x) is translated h units right and k units up.
__
Here, the function g(x) = x^2 is transformed to ...
f(x) = g(x -3) +12 = (x -3)^2 +12
Then the graph of f(x) is the graph of g(x)=x^2 translated 3 units right and 12 units up.

Figure A is similar to Figure B. What must always be true?
a.
The corresponding side lengths of A and B are proportional.
c.
The corresponding side lengths of A and B are equal.
b.
The corresponding side lengths of A are twice the corresponding side lengths of B.
d.
The corresponding side lengths of A are half the corresponding side lengths of B.
Answers
Option (a) is the correct answer. When two figures are similar, it means they have the same shape but different sizes.
How to solve the question?
In other words, their corresponding angles are congruent, and their corresponding side lengths are proportional.
Option (b) and (d) suggest that the corresponding side lengths of A and B are related by a constant factor (either 2 or 1/2). However, this is not necessarily true for all similar figures. The constant of proportionality can be any positive real number.
Option (c) suggests that the corresponding side lengths of A and B are equal, which means that A and B are not just similar but congruent. This is not necessarily true for all similar figures, as similar figures can differ in size.
Therefore, option (a) is the only answer that must always be true for similar figures. The corresponding side lengths of similar figures are proportional, which means that if one side of figure A is twice as long as a corresponding side of figure B, then all other corresponding sides will also be in the same ratio of 2:1. Similarly, if one side of figure A is three times as long as a corresponding side of figure B, then all other corresponding sides will also be in the same ratio of 3:1. This proportional relationship holds true for all pairs of corresponding sides in similar figures
To know more about similar visit :-
https://brainly.com/question/14285697
#SPJ1

Option (a) is the correct answer. The corresponding side lengths of A and B are proportional, must always be true if Figure A is similar to Figure B.
How to find if the figure is similar?When two figures are similar, their corresponding angles are congruent, and their corresponding side lengths are proportional. This means that if we take any two corresponding sides of the figures, the ratio of their lengths will be the same for all pairs of corresponding sides.
Option b and d cannot be true, as they both suggest a specific ratio of corresponding side lengths, which is not necessarily true for all similar figures.
Option c is not necessarily true, as two similar figures can have corresponding side lengths that are not equal but still have the same ratio.
To know more about similar visit :-
brainly.com/question/14285697
#SPJ1
In the figure, the area of trapezoid DBCE is 80 cm2
The ratio of the bases DE to BC is 3 : 5.
What is the area of triangle ADE, in square centimeters?
Answers
As the figure is not available here is a general method to solve this problem if you have the figure available. The area of triangle ADE is 45 cm2
Unfortunately, there is no figure attached to your question, so I cannot solve it accurately without knowing the dimensions of the trapezoid DBCE. However, I can provide you with a general method to solve this problem if you have the figure available:
Let trapezoid DBCE = A1
Let triangle ADE = A2
Let triangle ABC = A = A1 + A2 = BC × h/2
DE/BC = 3/5 = h2/h
h2 = 3/5 h
h = h1 + h2
h = h1 +3/5h
h1 = h - 3/5h
h1 = 2/5h
A2 = DE × h2 / 2
A2 = DE/2 × 3/5 h
A2 = DE × h × 3/10
DE × h = 10/3 A2
A1 = (BC + DE)/2 × h1
A1 = (BC + DE)/2 × 2/5h
A1 = BC/2 × 2/5h + DE/2 × 2/5h
A1 = (BC×h) / 2 ×2/5 + DE × h × 1/5
A1 = ( A1 + A2) × 2/5 + 10/3 × A2 ×1/5
A1 = (2/5×A1) + (2/5 ×A2) + (10/15 × A2)
A1 - 2/5A1 = 2/5A2 + 10/15A2
3/5 A1 = 6/15A2 + 10/15A2
3/5A1 = 6/15A2
3A1 = 16/3A2
A2 = 9/16 A1 (where, A1 = 80\(cm^{2}\) )
A2 = 9/16 × 80\(cm^{2}\)
A2 = 45 \(cm^{2}\)
The area of triangle ADE is 45 cm2
For more such questions on Trapezoid: brainly.com/question/8643562
#SPJ4
The correct question should be
In the figure, the area of trapezoid DBCE is 80 cm2. The ratio of the bases DE to BC is 3: 5. What is the area of triangle ADE, in square centimeters?

56.12 × 49= ???
send help
Answers
The answer is 3311.08, 56.12 * 49 = 3311.08
Answer:
2749.88
Step-by-step explanation:
THERES THE ANSWER have a NICE DAY!! B-)
What is the surface area of the box formed by the pattern below?
2 cm
3 cm
2 cm
6 cm
6 cm
3 cm
3 cm
3 cm
2 cm

Answers
The surface area of the box formed by the pattern is given as follows:
72 cm².
How to obtain the surface area of a figure?The surface area of a figure is calculated as the sum of the areas of all the components of a figure.
The components of the figure in this problem can be defined as follows:
A large rectangle with dimensions 6 cm and 2 + 3 + 2 + 3 = 10 cm.Two smaller rectangles with dimensions of 3 cm and 2 cm.The area of the large rectangle is given as follows:
6 x 10 = 60 cm².
The combined area of the smaller rectangles is given as follows:
2 x 3 x 2 = 12 cm².
Hence the surface area of the figure is given as follows:
60 + 12 = 72 cm².
More can be learned about the surface area at https://brainly.com/question/1310421
#SPJ1
You have 660 grams AP apples. What is your EP weight if the yield is 75 percent?
Answers
AP weight= 660g
Use the general slicing method to find the volume of the following solid. The solid with a semicircular base of radius 11 whose cross sections perpendicular to the base and parallel to the diameter are squares
Answers
The volume of the solid is 1789.33
For a circle of radius 11, we have the following equation:
x²+y²=11²
x²+y²=121
Now, making it explicit for x:
\(x=\sqrt{121-y^2}\)
Then, if we consider that for a height y, the length x is double, we have that the length of each cross-section is given by:
\(s=\sqrt[2]{81-y^2}\)
With this, we can propose the following integral to obtain the volume that they are asking us:
\(\int\limits^1_0 {s^2} \ \, dy \\\int\limits^1_0 ({\sqrt[2]{121-y^2})^2 } \, dy\\\\\int\limits^1_0 {4*(121-y^2)} \, dy\\\\4*(121y-\frac{y^3}{3} )\)
Finally, calculating, we have that the volume is V=1789.33
To know more about the volume of solid:
https://brainly.com/question/20284914
#SPJ4
Trucks in a delivery fleet travel a mean of 120 miles per day with a standard deviation of 18 miles per day. The mileage per day is distributed normally. Find the probability that a truck drives between 150 and 156 miles in a day. Round your answer to four decimal places.
Answers
The probability that a truck drives between 150 and 156 miles in a day is 0.0247. Using the standard normal distribution table, the required probability is calculated.
How to calculate the probability distribution?The formula for calculating the probability distribution for a random variable X, Z-score is calculated. I.e.,
Z = (X - μ)/σ
Where X - random variable; μ - mean; σ - standard deviation;
Then the probability is calculated by P(Z < x), using the values from the distribution table.
Calculation:The given data has the mean μ = 120 and the standard deviation σ = 18
Z- score for X =150:
Z = (150 - 120)/18
= 1.67
Z - score for X = 156:
Z = (156 - 120)/18
= 2
So, the probability distribution over these scores is
P(150 < X < 156) = P(1.67 < Z < 2)
⇒ P(Z < 2) - P(Z < 1.67)
From the standard distribution table,
P(Z < 2) = 0.97725 and P(Z < 1.67) = 0.95254
On substituting,
P(150 < X < 156) = 0.97725 - 0.95254 = 0.02471
Rounding off to four decimal places,
P(150 < X < 156) = 0.0247
Thus, the required probability is 0.0247.
Learn more about standard normal distribution here:
https://brainly.com/question/26822684
#SPJ1
Find the area of the triangle having the indicated angle and sides. (Round your answer to one decimal place.)
B 128°, a 86, c = 37

Answers
The area of the triangle with angle B = 128°, side a = 86, and side c = 37 is approximately 2302.7 square units.
To find the area of a triangle when one angle and two sides are given, we can use the formula for the area of a triangle:
Area = (1/2) * a * b * sin(C),
where a and b are the lengths of the two sides adjacent to the given angle C.
In this case, we have angle B = 128°, side a = 86, and side c = 37. To find side b, we can use the law of cosines:
c² = a² + b² - 2ab * cos(C),
where C is the angle opposite side c. Rearranging the formula, we have:
b² = a² + c² - 2ac * cos(C),
b² = 86² + 37² - 2 * 86 * 37 * cos(128°).
By substituting the given values and calculating, we find b ≈ 63.8.
Now, we can calculate the area using the formula:
Area = (1/2) * a * b * sin(C),
Area = (1/2) * 86 * 63.8 * sin(128°).
By substituting the values and calculating, we find the area of the triangle to be approximately 2302.7 square units.
For more question on area visit:
https://brainly.com/question/2607596
#SPJ8
PLS HELP THIS IS A TEST
Which number satisfies the inequality below?
1.75x + 4.50 < 20
a: 13
b: 14
c: 9
d: 7
Answers
Answer:
D: 7
Step-by-step explanation:
1.75 (7) + 4.50
12.25 + 4.50
= 16.75
16.75 < 20
Use Pascal's Triangle to expand (x^2-3y)^4
Answer


Answers
The expanded form of (x²-3y)⁴ using Pascal's Triangle is x⁸ - 12x⁶y² + 54x⁴y⁴ - 108x²y⁶ + 81y⁸.
What is Pascal's triangle?Pascal's Triangle is a triangular array of numbers in which the value in each cell is the sum of the two numbers directly above it.
To expand the given expression (x²-3y)⁴ as per Pascal's triangle:
First, write down the fourth row of Pascal's Triangle as:
1 4 6 4 1
The above numbers represent the coefficients of the terms in the expansion of (a+b)⁴, where a is x² and b is -3y. Therefore, it can be written as,
1×(x²)⁴ + 4×(x²)³×(-3y) + 6×(x²)²×(-3y)² + 4×(x²)(-3y)³ + 1(-3y)⁴
Simplify each term,
x⁸ - 12x⁶y² + 54x⁴y⁴ - 108x²y⁶ + 81y⁸
Therefore, the expanded form of (x²-3y)⁴ using Pascal's Triangle is x⁸ - 12x⁶y² + 54x⁴y⁴ - 108x²y⁶ + 81y⁸.
Learn more about Pascal's triangle here:
https://brainly.in/question/31891178
#SPJ1
D(5, 7), E(4, 3), and F(8, 2) form the vertices of a triangle. What is mZDEF?
Answers
Answer: \(m\angle DE F=90^{\circ}\)
Step-by-step explanation:
The slope of \(DE\) is \(\frac{7-3}{5-4}=4\).
The slope of \(EF\) is \(\frac{3-2}{4-8}=-\frac{1}{4}\).
Thus, \(DE \perp EF\), meaning \(m\angle DE F=90^{\circ}\).
how do you write the inequality -
"sixteen is less than a number"
Answers
Answer:
16<a number
Step-by-step explanation:
This is the less than symbol: <
16 is less than ( < ) a number
Lets put "a number" as x
16<x
Answer:
16 < n
Step-by-step explanation:
< - Less than. They way I remember is that the symbol is like an L.
n - Stands for number. You can use any letter I just chose that one.
Which expression is equivalent to 27 + 45?
Answers
Answer:
8 x 9
Have a nice day!
Ill give brainliest!!!!! I need the answers to this pleaseeee!!!!!!

Answers
Answer: both of them made ok estimates but i think issacs was better. hope this helps! ^-^
Step-by-step explanation:
A tennis tournament has 342 players. A single match involves 2 players. The winner of a match will play the winner of a match in the next round, whereas losers are eliminated from the tournament. The 2 players who have won all previous rounds play in the final game, and the winner wins the tournament. What is the total number of matches
Answers
Answer:
341 matches
Step-by-step explanation:
Given
\(Players = 342\)
\(Match = 2\ players\)
Required
Total number of matches.
The total number of matches is calculated by getting the number of matches in each round.
i.e.
\(Matches = \frac{Players}{2}\)
So, we have:
Round 1
\(Matches = \frac{342}{2} = 171\)
Round 2
\(Matches = \frac{171}{2} = 85\ R\ 1\) [R 1 means remainder 1]
Round 3
\(Matches = \frac{85 + 1}{2} = \frac{86}{2} = 43\)
[The remainder is added to each round]
Round 4
\(Matches = \frac{43}{2} = 21\ R\ 1\)
Round 5
\(Matches = \frac{21+1}{2} = \frac{22}{2} = 11\)
Round 6
\(Matches = \frac{11}{2} = 5\ R\ 1\)
Round 7
\(Matches = \frac{5+1}{2} = \frac{6}{2} =3\)
Round 8
\(Matches =\frac{3}{2} = 1 + 1\)
Round 9
\(Matches = \frac{1+1}{2} =\frac{2}{2} = 1\)
So, the total is:
\(Total = 171 + 85 + 43 +21 + 11 + 5 + 3 + 1+1\)
\(Total = 341\)
Find the area of the shaded region 10cm and 85 degrees. Help please!

Answers
The area of the shaded region is equal to 425π / 18 square centimeters.
How to determine the area of a circular sectionThe picture indicates us that we must find the area of the shaded region, consisting in a circular section with a measure of central angle of 85° and a radius of 10 centimeters. The area (A), in square centimeters, can be found by using the following formula:
A = (α / 360) · π · r²
Where:
α - Measure of the central angle, in degrees.r - Radius of the circular section, in centimeters.If we know that α = 85° and r = 10 cm, then the area of the shaded region is:
A = (85 / 360) · π · 10²
A = 425π / 18 cm²
The area of the shaded region is equal to 425π / 18 square centimeters.
To learn more on areas: https://brainly.com/question/27683633
#SPJ1
Please help and show how you found the answer step by step.
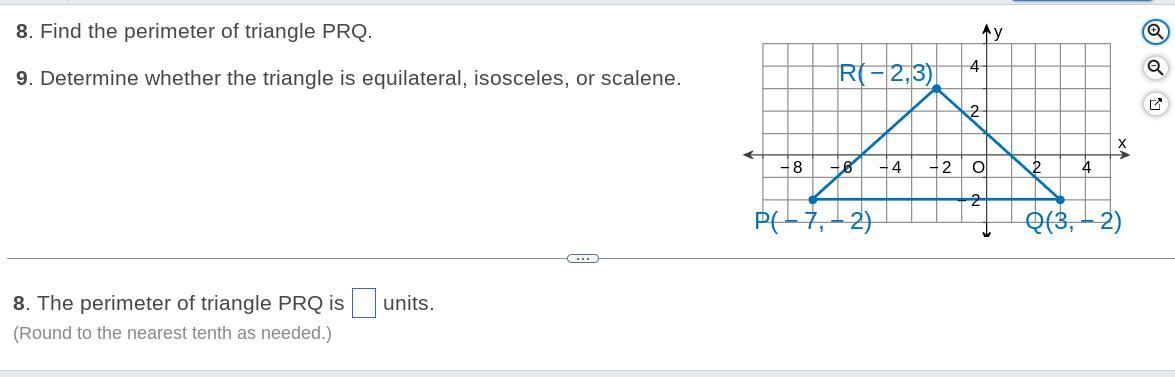
Answers
According to the information, the perimeter of the triangle is ≈ 31.18
How to calculate the perimeter of the triangle?To find the distance between two points, we can use the distance formula:
distance = sqrt((x2 - x1)^2 + (y2 - y1)^2)
Let's label the coordinates as follows:
Point 1: (-2, 3)
Point 2: (3, -2)
Now we can substitute these values into the distance formula:
distance = sqrt((3 - (-2))^2 + (-2 - 3)^2)
distance = sqrt((5)^2 + (-5)^2)
distance = sqrt(25 + 25)
distance = sqrt(50)
distance ≈ 7.07
Therefore, the distance from (-2, 3) to (3, -2) is approximately 7.07 units.
To find the perimeter of the triangle, we need to find the length of all three sides of the triangle and then add them up.
Using the distance formula, we can find the length of the sides:
Side 1: (-2,3) to (3,-2)
d = √[(3 - (-2))^2 + (-2 - 3)^2]
= √[5^2 + (-5)^2]
= √50
= 5√2
Side 2: (3,-2) to (-7,-2)
d = √[(-7 - 3)^2 + (-2 - (-2))^2]
= √[(-10)^2 + 0^2]
= 10
Side 3: (-7,-2) to (-2,3)
d = √[(-2 - (-7))^2 + (3 - (-2))^2]
= √[5^2 + 5^2]
= 5√2
Therefore, the perimeter of the triangle is:
5√2 + 10 + 5√2 = 15√2 + 10 ≈ 31.18 (rounded to two decimal places)
An two of the three sides are equal, so it is an isosceles triangle.
Lean more about isosceles triangle in: https://brainly.com/question/2456591
#SPJ1
Answer this question please

Answers
The possible rotation that transforms the image obtained from the reflection of the square ABCD on the line x = -1, with two vertices of the square remaining invariant is as presented as follows;
A rotation of the image of ABCD 270° counterclockwise, about the point (-2, -1) What is a rotation transformation?A rotation transformation is a transformation in which the preimage coordinate points are turned (in a circular manner) about a point.
The vertices of the square ABCD are; A(1, 4), B(3, 4), C(3, 2), D(1, 2)
The coordinates of the square following the reflection across the line x = -1 are; A'(-3, 4), B'(-5, 4), C'(-5, 2), and D'(-3, 2)
The rotation transformation of the image such that two vertices of the square are invariant (such that they remain the same) can be found as follows;
The rotation of a vertices of the image about the point (-2, -1) indicates the relative points are;
A'(-1, 5), B'(-3, 5), C'(-3, 3), and D'(-1, 3)
The image following a rotation of 270° are;
A''(5, 1), B'(5, 3), C'(3, 3), and D'(3, 1)
The above points relative to the origin are;
A''(5 + (-2), 1 - 1) = (3, 0), B''(5 - 2, -1 + 3) = (3, 2), C';(3 - 2, 3 - 1) = (1, 2), and D''(3 - 2, 1 - 1) = (1, 0)
A''(3, 0), B''(3, 2), C''(3, 4), and D''(1, 4)
The points (1, 2), and (3, 2) are therefore, the same as the points in the preimage and are therefore, invariant
The rotation is therefore;
A rotation of the image obtained from the reflection of the square, 270° counterclockwise about the point (-2, -1)Learn more on rotation transformation here: https://brainly.com/question/18392348
#SPJ1
Use the figure at the right for Exercises 1-3.
-
Can anyone help me pleaseee?

Answers
Answer:
TS is 3.7
UV is 7.9
SU is 6
Step-by-step explanation:
Determine whether each function is linear or nonlinear. Function Linear Nonlinear {(–1, 2), (0, 3), (1, 4), (2, 5)} Linear – {(–1, 2), (0, 3), (1, 4), (2, 5)} Nonlinear – {(–1, 2), (0, 3), (1, 4), (2, 5)} {(–3, 9), (–2, 4), (3, 9), (4, 16)} Linear – {(–3, 9), (–2, 4), (3, 9), (4, 16)} Nonlinear – {(–3, 9), (–2, 4), (3, 9), (4, 16)} y = –14x + 9 Linear – y = –14 x + 9 Nonlinear – y = –14 x + 9 y = x Linear – y = x Nonlinear – y = x
Answers
A. {(–1, 2), (0, 3), (1, 4), (2, 5)} → Non-linear function.
B. {(–3, 9), (–2, 4), (3, 9), (4, 16)} → Non-linear function.
C. y = –14x + 9 → Linear function
D. y = x → Linear function
What is a linear function?A linear function has a straight line as its graph. A linear function has the form shown below.
a + bx = y = f (x).
A linear function consists of one independent variable and one dependent variable. The independent and dependent variables are x and y, respectively.
When the absolute value of the input value of the function is connected to more than 1 output value, then the function is linear else it is a non-linear function.
From the given choices;
A. {(–1, 2), (0, 3), (1, 4), (2, 5)}
Here, the absolute value of 1 is connected to more than one point, so non-linear function.
B. {(–3, 9), (–2, 4), (3, 9), (4, 16)}
Here, the absolute value of 3 is connected to more than one point, so non-linear function.
C. y = –14x + 9 is equivalent to the slope-intercept form of linear function y = ax + b.
D. y = x is a linear function.
Therefore, B and D are linear functions.
To learn more about the linear function;
brainly.com/question/20286983
#SPJ9
Write the rational number -19 in the form of a fraction
Answers
the answer is 19/1
Answer the question in the picture

Answers
The area of the semicircle is A = 1187.9 cm².
What is the area of a circle?The area of a circle with a radius of r is A = πr².
Given that, the diameter of the semicircle is 55 cm.
The radius of the semicircle is,
r = 55/2
The area of a semicircle is given by,
A = (1/2)πr²
Substitute the values,
A = (1/2)π(55/2)²
A = 1187.9
Hence, the area of the semicircle is A = 1187.9 cm².
Learn more about the area of a circle:
https://brainly.com/question/22964077
#SPJ1
I NEED HELP WITH THIS QUESTION PLEASE NO LINKS!!!

Answers
Answer:
The answer should be 2 1/2
Step-by-step explanation:
Answer:
\( \longmapsto - 3 \frac{3}{8} - \frac{7}{8} \\ = - \frac{27}{8} - \frac{7}{8} \\ = \frac{ (- 27 - 7)}{8} \\ = \frac{( - 34)}{8} \\ = \frac{ (- 34) \div 2}{(8) \div 2} \\ = \frac{ - 17}{4} \\ = \boxed{ - 4 \frac{1}{4} }✓\)
- 4¼ is the right answer.