if you draw a card with a value of two or less from a standard deck of cards, i will pay you $452 . if not, you pay me $35 . (aces are considered the highest card in the deck.) step 1 of 2: find the expected value of the proposition. round your answer to two decimal places. losses must be expressed as negative values.
Answers
If you draw a card with a value of two or fewer from a standard deck of cards, I will pay you $452. if not, you pay me $35. Then, the expected value of the proposition is $2.46.
Firstly, calculate the probability of drawing a card with a value of two or less from a standard deck of cards. In a standard deck, there are 4 cards with a value of 2 (one for each suit). So, the probability of drawing a 2 is 4/52 or 1/13.
Now, calculate the expected value of the proposition. To do this, multiply the probability of each outcome by its respective payoff and sum the results. The expected value formula is as follows:
Expected value of the proposition = (Probability of winning) * (Amount won) + (Probability of losing) * (Amount lost)
Expected Value of the proposition = (1/13) * $452 + (12/13) * (-$35)
Expected Value of the proposition = $34.77 - $32.31
Expected Value of the proposition = $2.46
The expected value of the proposition is $2.46, meaning on average, you can expect to gain $2.46 for each card drawn in this game.
Learn more about probability:
https://brainly.com/question/5858025
#SPJ11
Related Questions
An individual has a utility function, U(q1,q2) = √q1 q2. (Mathematical assistance: √x= x^1/2). (a) Derive the individual's demand curve for q1 and q2 Hint: solve for the utility maximising values of q, and q2 for any set of prices (p1 and p2) and income (I). (b) Suppose p1 = £10 and p2 = £25 and total income is £100. Calculate the optimal consumption choices and the maximised utility value. (c) Compute the value for the Lagrange multiplier for the individual's budget constraint and explain its meaning.
Answers
(a) Derive demand curve by maximizing utility function.
(b) Optimal consumption: q1 = 4, q2 = 16; Maximized utility: U = 32.
(c) Lagrange multiplier represents marginal utility of income.
(a) To derive the individual's demand curve for q1 and q2, we maximize the utility function U(q1, q2) subject to the budget constraint. Let p1 and p2 represent the prices of goods q1 and q2, and I denote the individual's income.
The optimization problem can be formulated as follows:
Maximize U(q1, q2) = √(q1q2)
subject to the constraint: p1q1 + p2*q2 = I
By taking the partial derivatives of U with respect to q1 and q2, we can find the individual's demand functions. Setting these derivatives equal to zero and solving the resulting equations will give us the utility-maximizing values of q1 and q2 for any given prices and income.
(b) Given p1 = £10, p2 = £25, and total income I = £100, we can substitute these values into the demand functions derived in part (a) to find the optimal consumption choices. The maximized utility value can be calculated by substituting the optimal values of q1 and q2 into the utility function U(q1, q2).
(c) The Lagrange multiplier is a value associated with the constraint in an optimization problem. In this case, it represents the marginal utility of income or the rate at which the utility changes with respect to a small increase in income. It helps determine the optimal allocation of income between the two goods while satisfying the budget constraint.
Know more about the demand curve click here:
https://brainly.com/question/32623459
#SPJ11
Flat Rolling A 300-mm-wide strip 30-mm thick is fed through a rolling mill with two powered rolls each of radius =241 mm. The work thickness is to be reduced to 23.5 mm in one pass at a roll speed of 50rev/min. The work material has a flow curve defined by K=275MPa and n=0.15, and the coefficient of friction between the rolls and the work is assumed to be 0.10. Determine the maximum possible draft in mm. Give the answer down to the 2 nd decimal places
Answers
The maximum possible draft is 6.85 mm (rounded to the nearest hundredth).
The maximum possible draft is 6.85 mm (rounded to the nearest hundredth).
The given parameters for the flat rolling are:
Width of the strip (w) = 300 mm
Thickness of the strip before rolling (t₁) = 30 mm
Thickness of the strip after rolling (t₂) = 23.5 mm
Radius of the rolls (R) = 241 mm
Roll speed (N) = 50 rev/min
Coefficient of friction between rolls and work (μ) = 0.10
The flow curve of the material can be described using the following formula:
σ = Kεⁿ,
where
σ = Flow stress
K = Strength coefficient
ε = Strainn = Strain-hardening exponent
Since the material is assumed to have a flow curve defined by:
K = 275 MPa and
n = 0.15,
the formula can be rewritten as:
σ = 275ε^0.15
This equation will be used to calculate the rolling force.
First, the mean flow stress should be calculated.
This can be done using the following formula:
σ_avg = (1 / ε)∫[σ(ε)dε],
where
ε = (t₁ - t₂) / t₁
= (30 - 23.5) / 30
= 0.2167
σ = 275ε^0.15
Then,σ_avg = (1 / 0.2167)∫[275(ε^0.15)dε]
= 374.4 MPa
The maximum possible draft can be calculated using the following formula:
Maximum possible draft = (πR/2N)[(σ_avg/μ)ln(t₁/t₂)],
where, R
= 241 mm N
= 50 rev/minσ_avg
= 374.4 MPaμ
= 0.10t₁
= 30 mmt₂
= 23.5 mm
Maximum possible draft = (π × 241 / 2 × 50)[(374.4 / 0.10)ln(30 / 23.5)]
Maximum possible draft = 6.85 mm (rounded to the nearest hundredth)
Therefore, the maximum possible draft is 6.85 mm (rounded to the nearest hundredth).
To know more about maximum possible visit:
https://brainly.com/question/29130692
#SPJ11
I need help with this question
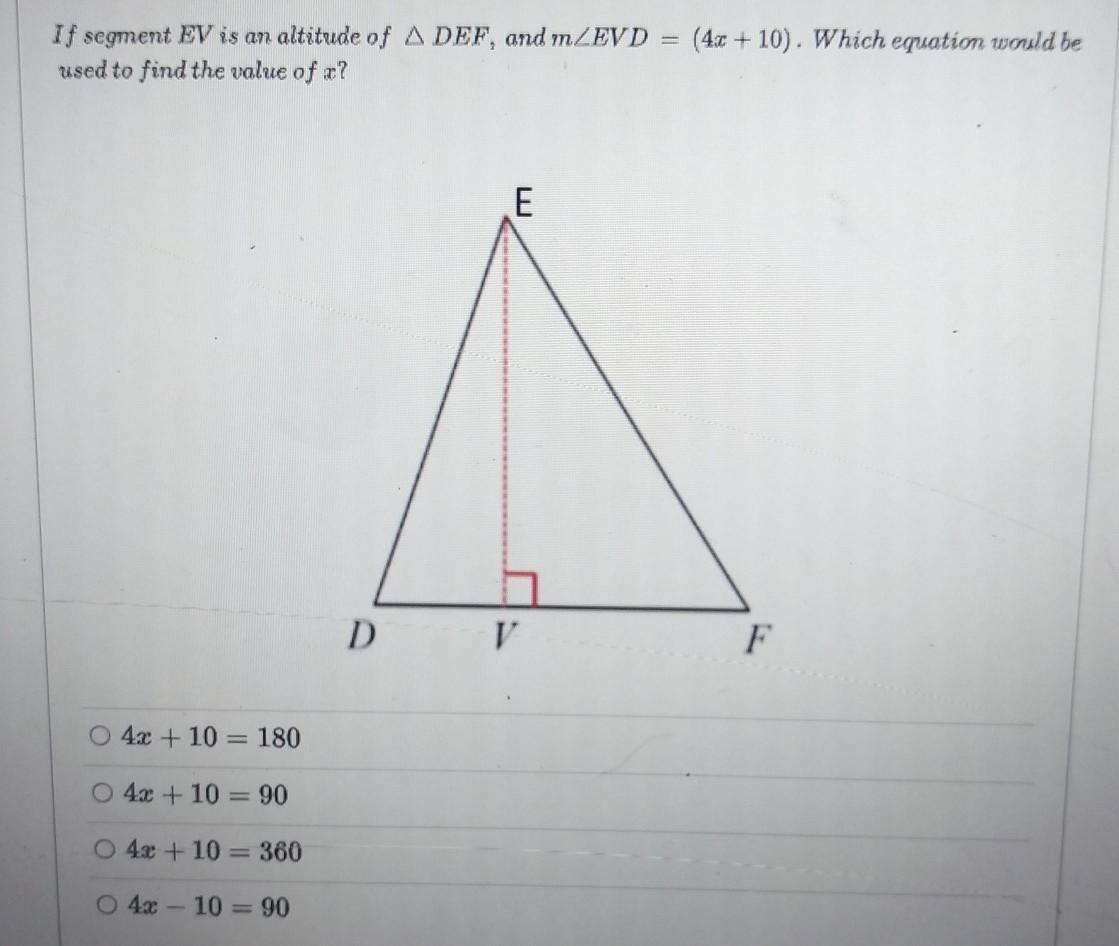
Answers
Answer:
4x+10=90.
Step-by-step explanation:
The angle EVD forms a right angle. right angles are equal to 90. if the angle is 90 and is shown by the equation 4x+10 then 4x+10=90
Kevin is 333 years older than Daniel. Two years ago, Kevin was 444 times as old as Daniel.
Let k be Kevin's age and let d be Daniel's age.
Which system of equations represents this situation?
Answers
Answer:
k = d + 3
k - 2 = 4( d - 2 )
Step-by-step explanation:
Let k be Kevin's age and Let d be Daniel's age.
Given : Kevin is 3 years older than Daniel.
i.e. Age of Kelvin = Age of Daniel+ 3
i.e. In terms of variables , k= d+3 (1)
Two years ago,
Age of Kelvin = k-2
Age of Daniel = d-2
Since Two years ago ,Kevin was 4 times as old as Daniel.
i.e. In terms of variables : k -2 = 4 x (d-2)
k-2=4(d-2) (2)
From (1) and (2) the system of equations represents this situation are
k = d + 3
k - 2 = 4 ( d - 2)
A. 264
B. 233
C. 153
D. 268

Answers
9514 1404 393
Answer:
A. 264 mi³
Step-by-step explanation:
The area of the right triangular base is ...
A = 1/2bh
A = 1/2(6 mi)(8 mi) = 24 mi²
Then the volume of the prism is ...
V = Bh . . . . . where B is the base area and h is the distance between bases
V = (24 mi²)(11 mi) = 264 mi³
Which of the following values cannot be probabilities?
1,
−0.49,
0,
1.45,
5/3,
2,
0.01,
Answers
The values that cannot be probabilities are -0.49 and 5/3.
The values that cannot be probabilities are -0.49 and 5/3.
A probability is a numerical value that lies between 0 and 1, inclusively. A value of 0 indicates that the event is impossible, whereas a value of 1 indicates that the event is certain. Every possible outcome's probability must be between 0 and 1, and the sum of all probabilities in the sample space must equal 1.
A probability of 1/2 means that the event has a 50-50 chance of occurring. Therefore, a value of 0.5 is a possible probability.1 is the highest probability, and it indicates that the event is certain to occur. As a result, 1 is a valid probability value. 0, on the other hand, indicates that the event will never happen.
As a result, 0 is a valid probability value.0.01 is a possible probability value. It is between 0 and 1, and it is not equal to either value.
1.45 is a possible probability value. It is between 0 and 1, and it is not equal to either value.
2, which is greater than 1, cannot be a probability value.
As a result, it is not a valid probability value. -0.49 is less than 0 and cannot be a probability value.
As a result, it is not a valid probability value. 5/3 is greater than 1 and cannot be a probability value.
As a result, it is not a valid probability value. Thus, the values that cannot be probabilities are -0.49 and 5/3.
Learn more about sample space visit:
brainly.com/question/30206035
#SPJ11
How to you write 1/25 using exponents
Answers
Answer:
\(5^{-2}\)
Step-by-step explanation:
Using the rule of exponents
\(a^{-m}\) ⇔ \(\frac{1}{a^{m} }\) , then
\(\frac{1}{25}\) = \(\frac{1}{5^{2} }\) = \(5^{-2}\)
In exponent form, it should be written as \(5^{-2}\).
Given that,
The fraction is \(\frac{1}{25}\)We need to write in the exponent form
Based on the above information, the calculation is as follows:
\(a^{-m} = \frac{1}{a^{m}} \\\\\frac{1}{25} = \frac{1}{5^{2}}\)
\(5^{-2}\)
Learn more: brainly.com/question/17429689
Find the distance from point X to line p.
Answers
The distance from point X to line p is 2√17 units.
We are given the point X as:
X = ( - 2 , 5 )
We need to find the distance of X from the line p.
We will do this by using the distance formula:
Distance = √ (y₂ - y₁)² + (x₂ - x₁)²
Distance = √ (- 2 - 0) ² - (5 - ( - 3)) ²
= √ ( - 2) ² - (5 + 3) ²
= √ ( - 2) ² - (8) ²
= √ 4 + 64
= √ 68
= 2 √17 units
Therefore, the distance from point X to line p is 2√17 units.
Learn more about distance here:
https://brainly.com/question/7243416
#SPJ9
Your question was incomplete. Please find the content below:
Find the distance from point X to line p. An image of a point X, a line p, and three segments joining the point and the line. Question 12 options:
A. 2 √34 units
B. √85 units
C. 2 √17 units
D. √17 units

Justin made a scale drawing of a city. The scale he used was 5 inches : 2 yards. A neighborhood park is 175 inches in the drawing. How wide is the actual park?
Answers
Answer:
68.8 yards
Step-by-step explanation:
We can do justice to this question using proportion,
Proportion in mathematics means that two ratios are equal it can be expressed as w/x = y/z
Let us denote the field on map as Z
Then we can say
5 inches on the map/ 2 yards in the park = 175inches/ X yards
If we cross multiply
5(Z )= 172 × 2
5(Z ) = 344
Make Z subject of the formula
Z= 344/5
Z= 68.8 yards
Hence the the actual park is 68.8 yards
SOMEONE PLEASE HELP ME WITH THIS I NEED TO PASS THIS PLEASE:/

Answers
Answer:
B
Step-by-step explanation:
the line has no slope
y = 5
Answer:
b
Step-by-step explanation:
Use the scale 1:150 and determine the actual length (in m) of a wall if the measured length on the plan is 5 cm
Answers
The actual length of a wall by using a scale of 1:150 is 7.5 m.
The drawing scale is the ratio of drawing size to actual size. To determine the scale of the drawing, we need to know about the formula first which is given by :
scale = drawing size : actual size
From that question, we know that :
scale = 1 : 150
drawing size = 5 cm
Based on the scale we can change the formula to
actual size = drawing size / scale
actual size = 5/ (1:150)
actual size = 5 x 150
actual size = 750 cm
Converting to the meter by dividing with 100
actual size = 750/100 m
actual size = 7.5 m
Hence, the actual length of a wall is 7.5 m
Find more on scale at: https://brainly.com/question/25324744
#SPJ4
PLEASE HELP !!!!!! WILL MARK THE BRAINLIEST

Answers
Answer:
c
hope its right :)
good luck!
Arrange the following integers from largest (top) to smallest (bottom). The integers are: − 90 , 87 , − 21 , 56 , 95 and 65.
Answers
The Arrangement of the given integers from largest (top) to smallest (bottom), will be: 95, 87, 65, 56, -21, -90.
What are the integers?Integers is one that is made up of whole numbers, comprising both positive and negative values, along with zero. There are no fractional or decimal components in integers. Integers refer to complete numbers that comprise positive and negative values, along with zero.
To arrange integers from largest to smallest, one can look at the numbers, compare and place in descending order. A good examples of integers are -3, -2, -1, 0, 1, 2, 3, etc.
Learn more about integers from
https://brainly.com/question/929808
#SPJ1
Find the total balance of each investment account earning simple annual interest. A: $624 at 5% for 3 years
$93. 60
B: $4,120 at 7% for 18 months
$432. 60
C: $900 at 3. 1% for 6 months
D: $275 at 4. 8% for 8 years
$105. 60
Answers
Answer:
the answer is A because if the interest is equal to 624×5×3÷100 which would give us 93.60
but for the rest the when you solve it you won't get the same answer below it
step 1 of 4 : state the null and alternative hypotheses in terms of the expected proportion for each day. write your answer as a fraction or a decimal rounded to six decimal places, if necessary.
Answers
By using the concept of testing of hypothesis, the null and alternative hypothesis is given by
\(H_0 :p_i = \frac{1}{5}\)
\(H_a : p_i \neq \frac{1}{5}\) for atleast one day
What is testing of hypothesis?
Suppose there is a hypothesis and there is a data at hand. Testing of Hypothesis determines whether a particular hypothesis is supported by the data at hand.
The null and alternative hypothesis can be written are as follows-
Null hypothesis: \(H_0\) : There is no difference in the number of swimmers from day to day.
Alternative hypothesis: \(H_a\) : There is a difference in the number of swimmers from day to day.
\(H_0 :p_i = \frac{1}{5}\)
\(H_a : p_i \neq \frac{1}{5}\) for atleast one day
To learn more about testing of hypothesis, refer to the link-
https://brainly.com/question/15980493
#SPJ4
Complete Question
The manager of the city pool has scheduled extra lifeguards to be on staff for Saturdays. However, he suspects that Fridays may be more popular than the other weekdays as well. If so, he will hire extra lifeguards for Fridays, too. In order to test his theory that the daily number of swimmers varies on weekdays, he records the number of swimmers each day for the first week of summer. Test the manager’s theory at the 0.10 level of significance.
Swimmers at the City Pool
Monday Tuesday Wednesday Thursday Friday
Number 46 68 43 51 70
Step 1 of 4 :
State the null and alternative hypotheses in terms of the expected proportion for each day. Enter your answer as a fraction or a decimal rounded to six decimal places, if necessary.
H0: pi=⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯
Ha: There is a difference in the number of swimmers from day to day.
The box plot shows the daily attendance at a Fitness Class. What is the median?

Answers
Answer:
40
Step-by-step explanation:
The median is the middle line of the box, which is the value 40. The lower quartile would be 35 and the upper quartile being 50.
N = r1N1 + ajNiN2, N2 = r2N2 + a2N2N where r1, 12, 41 and az are all positive constants. Determine the equilibria and their stabilities.
Answers
The equilibria of this system of equations can be found by solving the system of equations that results from setting each of the equations equal to zero.
From this system, we obtain two solutions, N1 = 0 and N2 = (a1r1)/(r2a2). The solution N1 = 0 indicates that no populations of individuals 1 exist in the environment. Meanwhile, the second solution, N2 = (a1r1)/(r2a2), indicates that an equilibrium population of N2 individuals is established.
The stability of both these equilibria can be determined by examining the eigenvalues of the Jacobian matrix. If the eigenvalues are negative, then the equilibria is stable and if they are positive, then the equilibria is unstable. The Jacobian matrix for this system is
|2r1 0|
|a1 -r2|.
know more about equations here
https://brainly.com/question/29538993#
#SPJ11
use the method of variation of parameters to solve the initial value problem x' = ax f(t), x(a) = xa using the following values. 4 -2 16t2 0 1 2t - 40 a= f(t) = x(0) = 2 - 1 4t t 1-2t x(t) =
Answers
The process involves finding the complementary solution x_c(t) by solving the homogeneous equation, determining the particular solution x_p(t) using the method of variation of parameters, and combining them to obtain the general solution x(t).
1. The method of variation of parameters can be used to solve the initial value problem x' = axf(t), x(a) = xa, where a and f(t) are given functions. In this case, we have the values a = 4 - 2t and f(t) = 16t^2. We need to find the solution x(t) using the initial condition x(0) = 2.
2. To solve the initial value problem using the method of variation of parameters, we first find the complementary solution x_c(t) by solving the homogeneous equation x' = ax.
3. For the given a = 4 - 2t, the homogeneous equation becomes x' = (4 - 2t)x. By separation of variables and integration, we find the complementary solution x_c(t) = Ce^(2t - t^2).
4. Next, we find the particular solution x_p(t) by assuming a particular solution of the form x_p(t) = u(t)e^(2t - t^2), where u(t) is a function to be determined.
5. Differentiating x_p(t) and substituting it into the original differential equation, we can solve for u'(t) and determine the form of u(t). After finding u(t), we substitute it back into x_p(t).
6. Finally, the general solution is given by x(t) = x_c(t) + x_p(t). By substituting the values and integrating, we can obtain the specific solution x(t) for the given initial condition.
Learn more about homogeneous equation here: brainly.com/question/12884496
#SPJ11
an emergency room nurse believes the number of upper respiratory infections is on the rise. the emergency room nurse would like to test the claim that the average number of cases of upper respiratory infections per day at the hospital is over 21 cases. using the computed test statistic of 2.50 and the critical value of 2.33, is there enough evidence for the emergency room nurse to reject the null hypothesis?
Answers
To determine whether there is enough evidence to reject the null hypothesis, we need to compare the computed test statistic to the critical value.
In this case, the computed test statistic is 2.50 and the critical value is 2.33. If the computed test statistic falls in the rejection region beyond the critical value, we can reject the null hypothesis. Conversely, if the computed test statistic falls within the non-rejection region, we fail to reject the null hypothesis.In this scenario, since the computed test statistic (2.50) is greater than the critical value (2.33), it falls in the rejection region. This means that the observed data is unlikely to occur if the null hypothesis were true.
Therefore, based on the given information, there is enough evidence for the emergency room nurse to reject the null hypothesis. This suggests that there is sufficient evidence to support the claim that the average number of cases of upper respiratory infections per day at the hospital is over 21 cases.
Learn more about statistic here
https://brainly.com/question/15525560
#SPJ11
There is enough evidence to reject the null hypothesis in this case because the computed test statistic (2.50) is higher than the critical value (2.33). This suggests the average number of daily respiratory infections exceeds 21, providing substantial evidence against the null hypothesis.
Explanation:Yes, there is enough evidence for the emergency room nurse to reject the null hypothesis. The null hypothesis is typically a claim of no difference or no effect. In this case, the null hypothesis would be an average of 21 upper respiratory infections per day. The test statistic computed (2.50) exceeds the critical value (2.33). This suggests that the average daily cases indeed exceed 21, hence providing enough evidence to reject the null hypothesis.
It's crucial to understand that when the test statistic is larger than the critical value, we reject the null hypothesis because the observed sample is inconsistent with the null hypothesis. The statistical test indicated a significant difference, upheld by the test statistic value of 2.50. The significance level (alpha) of 0.05 is a commonly used threshold for significance in scientific studies. In this context, the finding suggests that the increase in respiratory infection cases is statistically significant, and the null hypothesis can be rejected.
Learn more about the Null Hypothesis here:https://brainly.com/question/32386318
#SPJ11
An oil company purchased an option on land in Alaska. Preliminary geologic studies assigned the following prior probabilities.P(high-quality oil) = 0.50P(medium-quality oil)= 0.20P(no oil) = 0.30If required, round your answers to two decimal places.What is the probability of finding oil?
Answers
Since these are the only two categories that contain oil, the probability of finding oil is the sum of the probabilities of finding high-quality oil and medium-quality oil.
How to calculate and what is probability?Given that to find
P(finding oil) = P(high-quality oil) + P(medium-quality oil)
= 0.50 + 0.20
= 0.70
Thus the probability of finding oil is 0.70, or 70%.
Probability is a measure of how likely an event is to occur. It is a number between 0 and 1, with 0 indicating that the event is impossible and 1 indicating that the event is certain. The probability of an event is calculated by dividing the number of possible outcomes by the number of favourable outcomes.
To know more about probability visit:-
https://brainly.com/question/30034780
#SPJ1
Isabella is going to an amusement park. The price of admission into the park
is $20, and once she is inside the park, she will have to pay $2 for every ride
she rides on. How much money would Isabella have to pay in total if she goes
on 13 rides? How much would she have to pay if she goes on r rides?
Cost with 13 rides:
Cost with r rides:
Answers
Answer:
46$ in total
y=2r+20
If Isabella goes on 13 rides, she would have to pay a total of $46. If she rides 'r' times, the total cost would be expressed by the mathematical equation 20 + 2r.
Explanation:This question relates to a linear relationship involving a fixed cost and a variable cost. In Isabella's case, the fixed cost is the admission fee, which is $20. The variable cost is the rides, where each ride costs $2.
So, if she goes on 13 rides, she will have to pay: $20 (for admission) + ($2 * 13 (rides)) = $20 + $26 = $46.
For r rides, the total cost would be: $20 (for admission) + ($2 * r (rides)). So the total cost for r rides can be expressed in a mathematical equation as: 20 + 2r.
Learn more about Cost Calculation here:https://brainly.com/question/34783456
#SPJ2
HELP ME WITH MY MATH

Answers
Answer:
91 hundreths, (1*1)+(9*1/10), .19
<3 love from maddie
Answer:
(1*1)+(9*1/10) then 91 hundreths and last 0.19
Hope it helps!
800 children a day ride on the roller coaster, but another 200 are turned away because they're not tall enough. What proportion of the total number of children are turned away?
A) Half are turned away
B) One quarter are turned away
C) One fifth are turned away
Answers
Answer:
Step-by-step explanation:
C
Answer:
B
Step-by-step explanation:
Lee's uncle is installing a new pool in his backyard. The pool is a square and has an area of 121ft^2. He decides to build a 4 ft wide deck to surround the pool. What is the outside perimeter of the deck? The small square is the pool and the deck is the big square
Answers
Answer: 76 feet
Step-by-step explanation:
Given: The pool is a square and has an area of \(121ft^2\).
We know that , area = side²
⇒ side= √area
⇒ side= √121=11 feet
Width of deck =4 feet
Length of deck around pool = 11+4+4 = 19 feet
Outside perimeter of deck = 4 (19) = 76 feet [since perimeter of square = 4 (side)]
Hence, Outside perimeter of deck = 76 feet
Write the ratios as fractions IN THEIR SIMPLEST form
44 boys to 88 girls
Answers
Answer:
2:4
Step-by-step explanation:
In a tennis club there are 3 times as many right-handed players as there are left-handed players. If there are 72 players in total, how many are left-handed?
Answers
Answer 18
Step-by-step explanation:
x²-y²+x-y=0
can yall solve this is either or format
Answers
y-intercept: (0,0) (0, -1)
Salma is ordering 4 bags of cat food from Canada. Each bag has a mass of 2.5 kg. To determine the shipping costs, Salma needs to know the total weight in pounds. What is the weight of the cat food in pounds? Use 1 kg = 2.2 lb and do not round any computations.
Answers
5.5 pounds
Assume A is an n × n matrix. Answer "True" if the statement is always true, and "False" otherwise. a. If A is a stochastic matrix, then its 1-eigenspace must be a line. Choose ▼ b. If A is a stochastic matrix, then 1 must be an eigenvalue of A. Choose c. If A is a positive stochastic matrix, then repeated multiplication by A pushes each vector toward the 1-eigenspace. Choose d. If A is a square matrix, then A and A" must have the same eigenvalues. Choose ▼
Answers
The statements that is always true or false given that A is an n × n matrix are; A. True. B. True C. True, D. True
What should you know about n × n matrix?A. A stochastic matrix always has 1 as an eigenvalue, and the corresponding eigenvector forms a line, the 1-eigenspace. in other words, A stochastic matrix is a matrix whose rows sum to 1. This means that the sum of the elements in each row of A is equal to 1.
B. a stochastic matrix always has 1 as an eigenvalue. The eigenvalues of a matrix are the roots of its characteristic polynomial.
C. A positive stochastic matrix is a stochastic matrix whose entries are all non-negative. If A is a positive stochastic matrix, then repeated multiplication by A pushes each vector toward the 1-eigenspace.
D. For a square matrix, the eigenvalues of a matrix and its transpose are the same.
The above answer for D is based on the assumption that question D is
d. If A is a square matrix, then A and A^T must have the same eigenvalues.
Find more exercises on matrix;
https://brainly.com/question/11348342
#SPJ1
HELP!! out of the 4,500 people Who attended the rock concert 46% purchased a shirt how many people bought t-shirts??
Answers
Answer:
2070 people.
Step-by-step explanation:
We can set up the following proportion:
\(\frac{46}{100}=\frac{x}{4500}\)
Then, cross multiply, and you'll get your answer: 2070 people.
Hope this helped!
Answer:
2,070 people
Step-by-step explanation:
46% of 4,500 is 2,070
you can also solve this by doing 4,500 x .46 which will also give you 2,070
hope this helps :)