Answers
Answer:
to big of a blur to see
Step-by-step explanation:
Related Questions
point (x, y) is randomly picked from inside the rectangle with vertices (0, 0), (4, 0), (4, 1), and (0, 1). What is the probability that x < y
Answers
To solve this problem, let us first find the probability that x < y when point (x, y) is randomly selected from inside the rectangle. Then, using the area of the rectangle, normalize the probability.
The probability that x < y is 1/8.
To find the probability that x < y when a point is randomly chosen from within the rectangle. Let A be the area of the region where x < y, and B be the area of the rectangle. Then, the probability that x < y is given by P(x < y) = A/B. To find A and B, let us first look at the line x = y, which passes through (0,0) and (1,1) and separates the rectangle into two regions: Region I: The area to the right of the line x = y, where x > y. Region II: The area to the left of the line x = y, where x < y. region xy plane Region I has area B - A, and Region II has area A. Hence, B - A + A = B, which implies A/B = A/(B - A) = 1/2. Therefore, we only need to find A.
Let C be the triangle with vertices (0,0), (1,0), and (1,1). This triangle has area 1/2. Since the rectangle has height 1, the line x = y intersects the rectangle at a height of 1/2, which means that A is the area of the trapezoid with vertices (1/2, 0), (1, 0), (1, 1), and (1/2, 1/2).trapezoid xy plane. To find the area of this trapezoid, we can split it into a rectangle and a right triangle, as shown below: split trapezoid xy plane. The rectangle has base 1/2 and height 1, so its area is 1/2. The triangle has base 1/2 and height 1/2, so its area is 1/8. Hence, the area of the trapezoid is 1/2 + 1/8 = 5/8. Therefore, the probability that x < y is P(x < y) = A/B = (5/8) / 4 = 1/8.
Let's learn more about probability:
https://brainly.com/question/25839839
#SPJ11
help me out on this :)

Answers
Answer:
Answer is B
Step-by-step explanation:
y = -1
What is 24/240 as a decimal
Answers
Answer:
0.1
Step-by-step explanation:
Just take 24/24 which is 1 and move the decimal one place to the left because there is an extra 0 on the denominator
Please help me with this math problem

Answers
Answer:
what Type of question is that
To celebrate the first day of school, Reagan brought in a tray of caramel brownies and walnut brownies. The tray had a total of 20 brownies, of which 10% were caramel. How many caramel brownies did Reagan bring?
Answers
Answer:
2 were caramel
Step-by-step explanation:
1.5 of x is 30
Happy new year btw
Answers
happy new yearrrrrrrr
Answer:
20
Step-by-step explanation:
'of' means multiplication
'is' means equals
1.5x = 30
x = 30 ÷ 1.5
x = 20
What is the probability that either event will occur?
15
A
17
B
2
P(A or B) = P(A) + P(B)
P(A or B) = [?]
Answers
The probability that either event will occur is 0.83
What is the probability that either event will occur?From the question, we have the following parameters that can be used in our computation:
Event A = 18
Event B = 12
Other Events = 6
Using the above as a guide, we have the following:
Total = A + B + C
So, we have
Total = 18 + 12 + 6
Evaluate
Total = 36
So, we have
P(A) = 18/36
P(B) = 12/36
For either events, we have
P(A or B) = 30/36 = 0.83
Hence, the probability that either event will occur is 0.83
Read more about probability at
brainly.com/question/251701
#SPJ1
![What is the probability that either event will occur?15A17B2P(A or B) = P(A) + P(B)P(A or B) = [?]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/5dd7e3IsxzB7UDoPS50kjKaWnZ2gZOhz.jpeg)
PLEASE HELP EASY SLOPE MATH its not 1.5

Answers
Answer: The answer is 4.5
Answer:
B. 4.5 miles per hour
Step-by-step explanation:
look at the graph and see where the line hits 1(time in hours) as you can see, the line hits in between 3 and 6, so the most reasonable answer would be 4.5. this doesn't work for all answers, but it seems to work for this one. I hope that helps you!
If y varies directly as x and y = 5 when x = 0.4, find x when y = 37.5.
Answers
The value of x when y = 37.5 if y varies directly as x and y = 5 when x = 0.4 is 3
How to calculate direct variation?y = k × x
Where,
k = constant of proportionality
If y = 5 when x = 0.4
y = k × x
5 = k × 0.4
5 = 0.4k
divide both sides by 0.4
k = 5/0.4
k = 12.5
If y = 37.5, find x
y = k × x
37.5 = 12.5 × x
37.5 = 12.5x
divide both sides by 12.5
x = 37.5 / 12.5
x = 3
Therefore, the value of x when y = 37.5 is 3
Read more on direct variation:
https://brainly.com/question/6499629
#SPJ1
The value of x from y is x = 3
How to determine the value of x from yFrom the question, we have the following parameters that can be used in our computation:
y varies directly as x and y = 5 when x = 0.4,
The equation of direct variation is
k = y/x
So, we have
k = 5/0.4
Evaluate
k = 12.5
So, we have
y/x = 12.5
When y = 37.5. we have
37.5/x = 12.5
Solve for x
x = 3
Hence, the solution is x 3
Read more about direct variation at
https://brainly.com/question/6499629
#SPJ1
Suppose in your sample of 25 trucks, you found a sample mean of 19.58 cubic feet, and a standard deviation of 2.3 cubic feet. What test statistic and P-value result from this sample mean?

Answers
test static=0.0913,P-value=0.37
answer
6(u+3) Use the distributive property to remove the parentheses 6(u+3
Answers
Answer:
6u+18
Step-by-step explanation:
6*u=6u and 6*3=18
At the beginning of the school year, 118 students are enrolled in 4th grade. The students are divided into 6 classes. Which is the best estimate of the number of students in each class? *
A 10
B 20
C 30
D 40
Answers
Answer:
b. 20
Step-by-step explanation:
divide 118 by 6 and round to 20
Answer:
20 you will get me when you round it
For what value of x does 3²x _ g³x-4?
Answers
Answer:
\(x=2\)
Step-by-step explanation:
I believe your question is:
For what value of \(x\) does \(3^{2x}=9^{3x-4}\)?
—
First, rewrite \(9\) as \(3^2\):
\(3^{2x}=(3^2)^{3x-4}\)
Then, use exponentiation to apply the \((a^b)^c=a^{bc}\) rule:
\(3^{2x}=3^{2(3x-4)}\)
Rewrite the expression as a non-exponential one since the bases (\(3\)) are equal on both sides:
\(2x=2(3x-4)\)
Distribute the \(2\):
\(2x=6x-8\)
Subtract \(6x\) from both sides:
\(-4x=-8\)
Divide both sides by \(-4\):
\(x=2\)
4
x+1
=
\,\,256^{1}
256
1
Answers
The solution to the exponential equation 4^(x + 1) = 256 is given as follows:
x = 3.
How to solve the exponential equation?The exponential equation in this problem is defined as follows:
4^(x + 1) = 256
Both 4 and 256 are powers of 2, as follows:
4 = 2².256 = 2^8.Then, considering these simplifications of 4 and 256 as powers of 2, the exponential equation can be simplified as follows:
2^[2(x + 1)] = 2^8.
The exponential function 2^x is one-to-one, meaning that each input is mapped to a single output, hence we can solve for the variable x is follows.
2(x + 1) = 8
2x + 2 = 8
2x = 6
x = 6/2
x = 3.
This means that x = 3 is the solution to the exponential function presented in this problem.
More can be learned about exponential equations at https://brainly.com/question/2456547
#SPJ1
The diagnols of sqaure LMNP intersect at K. Given that LK= 1, find MP.

Answers
if LK = 1, then MP =1, since the diagonals of a square are equal and intersect at the center of the square
This follows that KN = 1 and KP = 1
Therefore, MP = MK + KP = 1 + 1 = 2
Carlos is solving 2x² - 8x = -7 by completing the square. His first few steps are shown below.
What number should he add to both sides of the equation?

Answers
Answer:4
Step-by-step explanation:i hoped ive helped u
Conduct
the hypothesis test and provide the test statistic, critical value and P-Value, and state the conclusion. A person randomly selected 100 credit
card purchases and recorded the cents portions of those amounts. The table below lists those cents portions categorized according to the indicated values. Use a 0.05 significance level to test the claim that the four categories are equally likely. The person expected that many checks for the whole dollar amounts would result in disproportionately high frequency for the first category, but do the results support that expectation?
Data set:
Cents portion 0-24 25-49 50-74 75-99
Number 56 18 14 12
Show all work:
The test statistic is __. (Round to three decimal places as needed).
The critical value is __. (round to 3 decimal places as needed).
The P-value is __. (Round to 4 decimal places a needed).
State the conclusion:
___
H 0 (below right). There ___ sufficient evidence to warrant rejection of the claim that the 4 categories are equally likely. The results ___ to support the expectation that the frequency for the first category is disproportionately high.
Answers
The test statistic (52) is less than the critical value (7.815), so the decision is fail to reject null hypothesis
In conclusion, there is insufficient evidence to support the claim that four categories are not equally likely at the significance level 0.05.
Given information:
The total number of checks (n) is 100.The total number of categories of cents portions (m) is 4.The level of significance is 0.05.The claim is that the four categories are equally likely.The statistical hypothesis is given by,
Null hypothesis \((H_0)\): The four categories of cents portion of check are equally likely.Alternative hypothesis \((H_a)\) : The four categories of cents portion of check are not equally likely.The expected frequency \((E_i)\) of each category is given by:
\(E_i=\frac{n}{m}\\ \\E_i=\frac{100}{4}\\ \\E_i=25\)
The calculation shown in the following table:
Categories \(O_i\) \(E_i\) \((O_i-E_i)^2\) \(\frac{(O_i-E_i)^2}{E_i}\)
0-24 56 25 961 38.44
25-49 18 25 49 1.96
50-74 14 25 121 4.84
75-99 12 25 169 6.76
Total 100 100 1300 52
Test statistic:
\(\chi^2=\sum^4_i_=_1\frac{(O_i-E_i)^2}{E_i}\)
= 52
Therefore, the value of chi-square test statistic is 52.
The degrees of freedom (df) is,
df = m - 1
= 4 - 1
= 3
The critical value obtained from the chi-square table at the degrees of freedom 3 and the significance level 0.05 is 7.815
Thus, the obtained critical value is 7.815.
Since the test statistic (52) is less than the critical value (7.815), so the decision is fail to reject null hypothesis
In conclusion, there is insufficient evidence to support the claim that four categories are not equally likely at the significance level 0.05.
Learn more about statistical hypothesis at:
https://brainly.com/question/29576929
#SPJ4
Give the following non-linear equation: z = x² + 4xy + 6xy² 1.1. Linearize the following equation in the region defined by 8 ≤x≤10,2 ≤y ≤4. (8) 1.2. Find the error if the linearized equation is used to calculate the value of z when x = 8, y = 2.
Answers
The linearized equation for the non-linear equation z = x² + 4xy + 6xy² in the region defined by 8 ≤ x ≤ 10, 2 ≤ y ≤ 4 is given by :
z ≈ 244 + 20(x - 8) + 128(y - 2).
When using the linearized equation to calculate the value of z at x = 8, y = 2, the error is 0.
1.1. To linearize the equation in the given region, we need to find the partial derivatives of z with respect to x and y:
∂z/∂x = 2x + 4y
∂z/∂y = 4x + 6xy
At the point (x₀, y₀) = (8, 2), we substitute these values:
∂z/∂x = 2(8) + 4(2) = 16 + 8 = 24
∂z/∂y = 4(8) + 6(8)(2) = 32 + 96 = 128
The linearized equation is given by:
z ≈ z₀ + ∂z/∂x * (x - x₀) + ∂z/∂y * (y - y₀)
Substituting the values, we get:
z ≈ z₀ + 24 * (x - 8) + 128 * (y - 2)
1.2. To find the error when using the linearized equation to calculate the value of z at x = 8, y = 2, we substitute these values:
z ≈ z₀ + 24 * (8 - 8) + 128 * (2 - 2)
= z₀
Therefore, the linearized equation gives the exact value of z at x = 8, y = 2, and the error is 0.
To learn more about linearized equation visit : https://brainly.com/question/2030026
#SPJ11
Which set of side lengths can be used to construct a triangle?
OPTIONS
3, 4, 9
3, 5, 7
3, 5, 8
2, 6, 8
Answers
The value of set of side lengths can be used to construct a triangle are,
⇒ 3, 5, 7
We have to given that;
To find the set of side lengths can be used to construct a triangle.
Now, We know that;
The sum of two side of a triangle is always greater than third side.
Hence, We can check all options as;
⇒ 3, 4, 9
Since, 3 + 4 = 7 < 9
Hence, It does not form a triangle.
⇒ 3, 5, 7
Since, 3 + 5 = 8 > 7
Hence, It form a triangle.
⇒ 3,5, 8
Since, 3 + 5 = 8 = 8
Hence, It does not form a triangle.
⇒ 2, 6, 8
Since, 2 + 6 = 8 = 8
Hence, It does not form a triangle.
Thus, The value of set of side lengths can be used to construct a triangle are,
⇒ 3, 5, 7
Learn more about the triangle visit;
brainly.com/question/1058720
#SPJ1
How is p-value calculated with example?
Answers
To calculate the p-value, we have to follow the following steps:
First, identify the correct test statistic.Then, calculate the test statistic using the relevant properties of the sample.Specify the characteristics of the test statistic’s sampling distribution.Then, place test statistics in the sampling distribution to find the p-value.To calculate the p-value, we need
p = sample proportion
p' = assumed population proportion in the null hypothesis
n = sample size
Example
Given, n =40, σ = 32.17 and X = 105.37. calculate p-value.
σₓ = σ/ √n
σₓ = 32.17 / √40
= 5.0865
Now, by applying the test static formula, we get
t = (105.37 – 120) / 5.0865
t = -2.8762
Using the table, we find the value of P(t>-2.8762)
From the table, we get
P (t<-2.8762) = P(t>2.8762) = 0.003
If P(t>-2.8762) = 1- 0.003 = 0.997
P- value = 0.997 > 0.05
To learn more about the p-value from the given link
https://brainly.com/question/13786078
#SPJ4
what is ml to quarts?
Answers
One millimeter is equal to 0.00106 of U.S. liquid quarts. Simply multiply any number of ml with the given value of liquid quarts to convert and find volume.
An object's or space's three-dimensional extent can be measured using a volumetric unit of measurement. Capacity is measured by volume. Consequently, the volumetric unit is essentially a unit for gauging the size or extent of an object or space.
Typically, the unit is used to describe the volume of products or liquids. To measure a quantity of something, use the International System of Units. Despite the fact that people speak different languages, the SI Units are used globally to communicate the measurements used in research settings.
Cubic meters, liters, and milliliters are the three most popular SI units for measuring volume. Specifically, the cubic meter as the unit of volume in the SI system.
To learn more about unit of volume: https://brainly.com/question/1789840
#SPJ4
if 45 cookies will serve 15 students how many cookies are needed for 30 students
Answers
Answer: 30
Step-by-step explanation:
this is so easy
Answer:
1for 30 students i would need 90
private nonprofit four-year colleges charge, on average, $26,640 per year in tuition and fees. the standard deviation is $6,617. assume the distribution is normal. let x be the cost for a randomly selected college.
Answers
Using the given average cost, standard deviation, and assuming a normal distribution, we can determine the probability that the cost for a randomly selected college is more than a certain value.
The average cost of tuition and fees at private nonprofit four-year colleges is $26,640 per year, with a standard deviation of $6,617. Assuming a normal distribution, let x represent the cost for a randomly selected college.
To find the probability that x is more than a certain value, we can use the Z-score formula: Z = (x - mean) / standard deviation.
To find the probability that x is more than a certain value, we can use the Z-score formula: Z = (x - mean) / standard deviation.
Let's say we want to find the probability that x is more than $30,000.
Z = (30000 - 26640) / 6617
Z = 0.051
Using a Z-table or calculator, we can find the corresponding probability to be approximately 0.4801. This means that there is a 48.01% chance that the cost for a randomly selected college is more than $30,000.
In conclusion, using the given average cost, standard deviation, and assuming a normal distribution, we can determine the probability that the cost for a randomly selected college is more than a certain value.
To know more about probability visit:
https://brainly.com/question/31828911
#SPJ11
Find the average value of f(x)=−5x4+4x−10
over the interval [−2 , 2]
-104
335
67
26
-67
-151
151
-335
104
-26
Answers
Answer:
Step-by-step explanation:
the answer is f(x)= -5x4+4x-10 over [-2,2]
(9+7i)+(-5-31) =
add complex numbers
Answers
Answer:
4 + 4i
Step-by-step explanation:
Add the real part and add the imaginary part.
9 + 7i + (-5 - 3i) = 9 + 7i - 5 - 3i
= 9 - 5 + 7i - 3i
= 4 + 4i
Answer:
44
Step-by-step explanation:
Okay so we are given (9 + 71) + (-5 - 31).
We need to figure out the value of this expression.
First, let's solve the expression (9 + 71).
1. (9 + 71) = 80.
Now we have 80 + (-5 - 31).
Next, let's solve the expression (-5 - 31).
2. (-5 - 31) = -36.
We're left with 80 + (-36).
Finally, let's add the two numbers together.
80 + (-36) = 44
So (9 + 71) + (-5 - 31) = 44
Feel free to give brainliest.
Have an excellent day!
The most important component when reporting a numerical scientific result is the ______.
Answers
The most important component when reporting a numerical scientific result is the unit.
This is further explained below.
What is a numerical scientific result?Generally, Our work in numerical and scientific computing includes the creation, analysis, and implementation of computer algorithms with the purpose of finding mathematical solutions to issues originating in engineering and the sciences.
In conclusion, When presenting a numerical result from scientific research, the unit is the single most crucial component.
Read more about the numerical scientific result
https://brainly.com/question/19900863
#SPJ4
what is 35.7/0.07 x 100/100
Answers
Answer:
510
Step-by-step explanation:
100 / 100 = 1
35.7/0.07 = 510
510 * 1 = 510
use the values of the vertex and point to write the equation of the graph in standard form

Answers
The vertex form of a quadratic function is:
\(\begin{gathered} y=a(x-h)^2+k \\ \text{ Where} \\ (h,k)\text{ is the vertex of the parabola } \end{gathered}\)The standard form of a quadratic function is:
\(y=ax^2+bx+c\)We can do the following steps to solve the exercise.
Step 1: We replace the values of h,k, x, and y into the vertex form of a quadratic equation, and we solve for a.
\(\begin{gathered} h=1 \\ k=-5 \\ x=3 \\ y=-1 \end{gathered}\)\(\begin{gathered} y=a(x-h)^{2}+k \\ -1=a(3-1)^2-5 \\ -1=a(2)^2-5 \\ -1=4a-5 \\ \text{ Add 5 from both sides} \\ -1+5=4a-5+5 \\ 4=4a \\ \text{ Divide by 4 from both sides} \\ \frac{4}{4}=\frac{4a}{4} \\ 1=a \end{gathered}\)Step 2: We replace the values of a,h, and k into the vertex form of a quadratic equation.
\(\begin{gathered} y=a(x-h)^{2}+k \\ y=1(x-1)^2-5 \end{gathered}\)Step 3: We expand the expression inside the parentheses and combine like terms to convert the function into its standard form.
\(\begin{gathered} y=1(x-1)^{2}-5 \\ y=(x-1)^2-5 \\ y=(x-1)(x-1)-5 \\ \text{ Apply the distributive property} \\ y=x(x-1)-1(x-1)-5 \\ y=x*x-x*1-1*x-1*-1-5 \\ y=x^2-x-x+1-5 \\ y=x^2-2x-4 \end{gathered}\)AnswerThe equation of the graph in standard form is:
\(y=x^{2}-2x-4\)A point (8, c) lies on the line y = 3x + 2. Work out the value of c.
Answers
y=3*8+2=26
Therefor the answer for c is 26
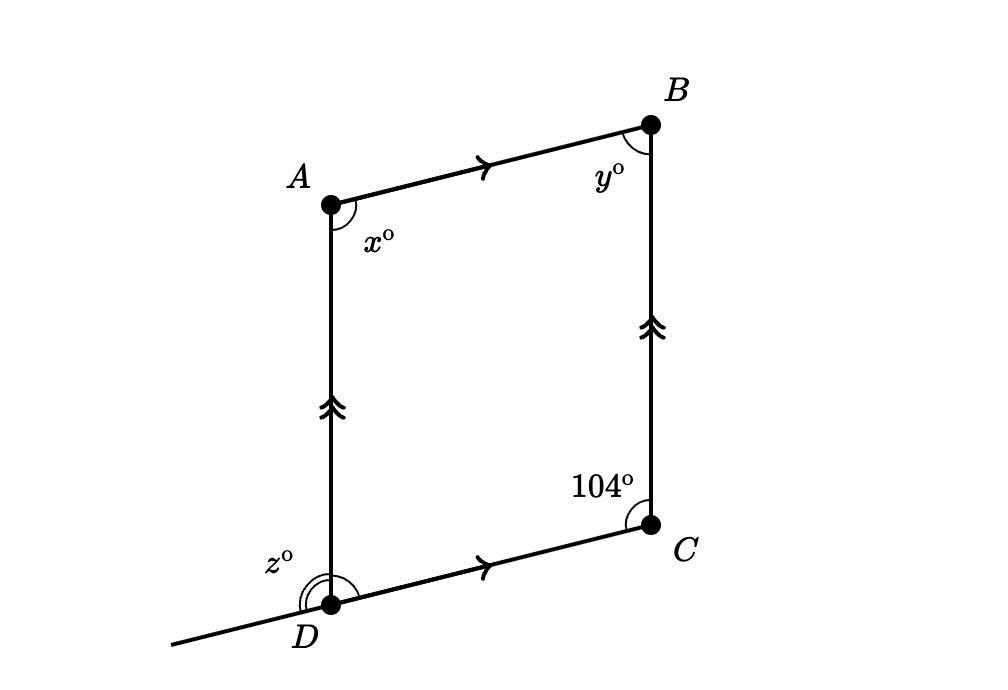
Side and angle properties of a parallelogram (level 2)
find x,y,z