If u(x) = -2x² +3 and V(x) =
X
what is the range of (u.v)(x)?
Answers
The range of u(x) = {-15, -5,1,3,1, -5, -15} and range of v(x)= {-3,-2, -1,0,1,2,3} for the domain of x = { -3,-2,-1,0,1,2,3}
What is domain and range?The domain of a function is defined by the set of the values of independent variables and the ranges are the set of values of dependent variables.
The domains act as an input of function where ranges act as an output.
How to find domain and range?We select domain randomly as domain are the set of independent variables. But how will be the ranges must depend on the function given us.
we are given 2 function u(x) = -2x²+3 and v(x)
for the 1st function the set of domain and ranges are different, but the domain and ranges have the same values for the 2nd function.
we select domain x= {-3, -2, -1, 0, 1, 2, 3}
the ranges for u(x) ={ -15, -5, 1, 3, 1, -5 , -15}
because, u(-3) = -2(-3)²+3 = -15
u(-2) = -2(-2)²+3 =-5
u(0) = 3
similarly, for the same set of x value, v(-3) = -3
v(-2) = -2
v(0) =0
to know more about range and domain visit:
https://brainly.com/question/26098895
#SPJ1
Related Questions
Please help, this chapter was on derivatives...

Answers
================================================
Work Shown:
Before we can use derivatives, we need to find the value of s when (x,y) = (15,20)
s^2 = x^2+y^2
s^2 = 15^2+20^2
s^2 = 225+400
s^2 = 625
s = sqrt(625)
s = 25
-----------
Now we can apply the derivative to both sides to get the following. Don't forget to use the chain rule.
s^2 = x^2 + y^2
d/dt[s^2] = d/dt[x^2 + y^2]
d/dt[s^2] = d/dt[x^2] + d/dt[y^2]
2s*ds/dt = 2x*dx/dt + 2y*dy/dt
2(25)*ds/dt = 2(15)*5 + 2(20)*(10)
50*ds/dt = 150 + 400
50*ds/dt = 550
ds/dt = 550/50
ds/dt = 11
-----------
Side note: The information t = 40 is never used. It's just extra info.
Indicate whether the following statements are True (T) or False (F). The quotient of two rational numbers is always a real number (provided the denominator is non-zero). 2. The ratio of two rational numbers is always positive 3. The difference of two rational numbers is always a rational number. 4. The difference of two rational numbers is always a natural number. 5. The quotient of two rational numbers is always a rational number (provided the denominator is non-zero). 6. The sum of two rational numbers is always a rational number. 7. The product of two rational numbers is always a rational number.
Answers
The true and false statements from the given options are classified below -
What are rational numbers?A rational number is a number that can be expressed in the form of p/q, where [p] and [q] of two integers and denominator [q] cannot be zero.
Given are the sentences describing the properties of rational numbers.
The statements which are true from the given ones are as follows -
The difference of two rational numbers is always a natural number.The difference of two rational numbers is always a rational number.The quotient of two rational numbers is always a rational number (provided the denominator is non-zero).The statements which are false from the given ones are as follows -
The ratio of two rational numbers is always positive. The quotient of two rational numbers is always a real number (provided the denominator is non-zero)The sum of two rational numbers is always a rational number.The product of two rational numbers is always a rational number.Therefore, the true and false statements from the given options are classified above.
To solve more questions on rational numbers, visit the link below-
https://brainly.com/question/1621669
#SPJ1
f(x)=x^3+5x+k and x+2 is a factor of f(x), then what is the value of k?
Answers
The value of k is 18.
If x + 2 is a factor of f(x) = x^3 + 5x + k, it means that when x = -2, the expression f(x) becomes zero.
Substituting x = -2 into f(x), we have:
f(-2) = (-2)³ + 5(-2) + k
= -8 - 10 + k
= -18 + k
Since f(-2) should equal zero, we have:
-18 + k = 0
k = 18
Therefore, the value of k is 18.
Learn more about Factor here:
https://brainly.com/question/30612677
#SPJ1
Answer for the question

Answers
Answer:
it is the domain
Step-by-step explanation:
because if you put 5x on the other side it will be a -5
PLEASE HELP ME ON QUESTION ASAP!!
IF YOU HAVE A TOPIC LIST IN YOUR EXAMS AND IT SAYS AVERAGES AND THE RANGE ARE YOU GOING TO BE HAVING MEAN AND RANGE IN YOUR TEST OR MEAN, RANGE MODE, MIDPOINT BASICALLY ALL OF IT ? IF ANSWERS CORRECT ILL RATE YOU FIVE STARS, GIVE YOU A THANKS AND MAYBE EVEN BRAINLIEST (sorry for caps)
Answers
Answer:
Step-by-step explanation:
Typically yes you need to know
Mean
Median
Mode
and Range
Mean = average, add all numbers then divide by how many
Median = midpoint, middle number. Be sure to list numbers from small to large if there are 2 middle numbers (this happens when there are an even amount), take the average of the 2 middle numbers
Mode = numbers that occurs the most in the list of numbers
Range = This is the largest number minus the smallest number.
4r^2+3s^2-rs r=-1 S=3
Need help with steps because everyone keeps saying it’s 26 but I get 28
Answers
Answer:
34
Step-by-step explanation:
4r² + 3s² - rs ← substitute r = - 1, s = 3 into the expression
= 4(- 1)² + 3(3)² - (- 1)(3)
= 4(1) + 3(9) - (- 3)
= 4 + 27 + 3
= 34
This may be hard to put together, but I need help with an angle equation. I'm looking for example equations and how to do these types of equations. *please note that this equation is completely random and probably ends with an ugly number. it's just an example of a type of problem*

Answers
Example: (2x - 4) x=7 so (2x (x=7) - 4) =18
suppose a b and c are integers and that htere is a solution to the linear diophantine equation ax by
Answers
The linear Diophantine equation k = x'x+y'y has integer solutions, say x' = x and y' = y
Linear Diophantine equations are a special class of equations in which we are looking for integer solutions instead of real ones. These equations play a vital role in number theory, cryptography, and computer science.
The given linear Diophantine equation is ax+by=c, where a, b, and c are integers, and x, y are unknowns that we are looking for. Suppose there is a solution to this equation, i.e., we can find integers x and y that satisfy this equation. Then, we can say that 'c' must satisfy a specific condition.
To understand this condition, we need to introduce the concept of the greatest common divisor (GCD) of two integers. The GCD of two integers a and b is the largest positive integer that divides both a and b without leaving a remainder. We denote the GCD of a and b by (a, b).
Now, the condition that 'c' must satisfy is given by the following theorem.
Theorem: A necessary and sufficient condition for the linear Diophantine equation ax+by=c to have an integer solution (x, y) is that (a, b) divides c.
Suppose there is an integer solution (x, y) to the given equation. Then, we can write:
c = ax+by
Let d be the GCD of a and b, i.e., d = (a, b). We can express a and b in terms of d as follows:
a = dm and b = dn, where m and n are integers.
Substituting these values of a and b in the given equation, we get:
c = dmx+dny
Dividing both sides by d, we get:
(c/d) = mx+ny
Since m, n, x, and y are integers, (c/d) must also be an integer. This means that (a, b) divides c, i.e., (a, b) | c.
Conversely, suppose (a, b) | c. Then, we can write c = k(a, b) for some integer k. Now, we need to show that there exist integers x and y that satisfy the equation ax+by=c.
Since (a, b) divides a and b, we can write:
a = (a, b)x' and b = (a, b)y'
where x' and y' are integers. Substituting these values of a and b in the given equation, we get:
k(a, b) = (a, b)x'x+(a, b)y'y
Dividing both sides by (a, b), we get:
k = x'x+y'y
This is a linear Diophantine equation in x' and y' with constant term k. It is a well-known fact that such equations have integer solutions if and only if (k, (a, b)) = d, where d = GCD(k, (a, b)).
But we know that (k, (a, b)) = (k, c), since (a, b) divides c. Hence, we have:
d = (k, c) = (x'x+y'y, k(a, b)) = (x'x+y'y, ka, kb)
But d divides ka and kb, since it is a common divisor of a and b. Hence, d divides x'x+y'y.
To know more about equation here.
https://brainly.com/question/10413253
#SPJ4
Complete Question:
Suppose a,b, and c are integers and that there is a solution to the linear Diophantine equation ax+by=c, that is, suppose there are integers x and y that satisfy the equation ax+by=c. what condition must c satisfy in terms of a and b?
Write a linear function f(x) = mx + b for the graph.

Answers
We write the linear function as f(x)=3.5x+1 for the graph.
What is linear function?
Linear function means a linear equation. As per given statement, we need to write an equation for straight line. We are given four-point in the XY coordinate.
How to write linear function with points?
We use the formula line passes through two points. The required function
should be in the form f(x) =mx+b or y=mx+b
given points are (0,1) (1,4.5) , (-1,-2.5) (-2,-6)
slope of line passes through first two points is=m= (y₂-y₁)/(x₂-x₁)= 3.5
slop of last two points is = m= 3.5
hence, four points lies in the same straight line
the equation of line, y= 3.5x+b
as the line passes through (-2,-6)
-6=3.5×(-2)+b
b=1, b is a constant
hence, the linear function is f(x)=y=3.5x+1
to learn more about linear function visit:
https://brainly.com/question/30045139
#SPJ1
The triangle shown has an area of 46 square centimeters. Find the measure of the base (segment AB ). Triangle A B C. A line goes from point C to point D on side A B. Side A C is 11 centimeters, C B is 9 centimeters, and A B is question mark.
Answers
By answering the presented question, we may conclude that Therefore, triangle the length of the base AB is approximately 20.88 centimeters.
What precisely is a triangle?A triangle is a closed, double-symmetrical shape composed of three line segments known as sides that intersect at three places known as vertices. Triangles are distinguished by their sides and angles. Triangles can be equilateral (all factions equal), isosceles, or scalene based on their sides. Triangles are classified as acute (all angles are fewer than 90 degrees), good (one angle is equal to 90 degrees), or orbicular (all angles are higher than 90 degrees) (all angles greater than 90 degrees). The region of a triangle can be calculated using the formula A = (1/2)bh, where an is the neighbourhood, b is the triangle's base, and h is the triangle's height.
the length of the base AB,
Area = (1/2) * base * height
\(CB^2 = CD^2 + BD^2\\9^2 = x^2 + (AB - x)^2\\81 = x^2 + (AB^2 - 2ABx + x^2)\\AB^2 - 2ABx + 2x^2 = 81\\\)
We also know that the area of the triangle is:
\(46 = (1/2) * AB * CB\\46 = (1/2) * AB * \sqrt(x^2 + 81)\\Now we can solve for AB in terms of x:AB = (2 * 46) / \sqrt(x^2 + 81)\\AB = 92 / \sqrt(x^2 + 81)\\(92 / \sqrt(x^2 + 81))^2 - 2(92 / \sqrt(x^2 + 81))x + 2x^2 = 81\\\)
\(8464 / (x^2 + 81) - (184x) /sqrt(x^2 + 81) + 2x^2 = 81\\8464 - 184x(x^2 + 81) + 2x^2(x^2 + 81) * sqrt(x^2 + 81) = 81(x^2 + 81)\\2x^4 - 181x^2 + 7743 = 0\\x^2 = (181 + \sqrt(181^2 - 427743)) / (2*2)\\x^2 = (181 + sqrt(129961)) / 4\\x^2 = (181 + 361) / 4\\x^2 = 90^2 / 4\\x = 45\sqrt(2) / 2\\\)
\(AB = 92 / \sqrt(x^2 + 81)\\AB = 92 / \sqrt((45sqrt(2) / 2)^2 + 81)\\AB = 92 / \sqrt(4050)\\AB ≈ 20.88 cm\\\)
Therefore, the length of the base AB is approximately 20.88 centimeters.
To know more about triangle visit:
https://brainly.com/question/2773823
#SPJ1
Question 2/2
Question 1 Part B (01.02, 01.03 MC): A boutique owner needs to sell $1,200 in clothing each week. This week, she is within $125 of
her goal.
What does the variable in the equation represent? (2 points)
4 of 19
Back
A. Amount the owner needs to sell
B. Price per item
C. Number of items sold
D. Total sales for the month
1 answer(s) selected
Open notes navigator A

Answers
A boutique owner needs to sell $1,200 in clothing each week. This week, she is within $125 of her goal. The variable in the equation is
C. Number of items soldWhat is variable in math?A variable is a quantity that could change depending on the circumstances of an experiment or mathematical problem.
Typically, a variable is denoted by a single letter. The general symbols for variables most frequently used are the letters x, y, and z.
In the context of the problem, the boutique owner wants to make $1,200 in clothing each week. This amount in made by the number of items sold as this is added to get to the amount the boutique owner is targeting
Learn more about variable:
https://brainly.com/question/25223322
#SPJ1
What are the coordinates of the point on the directed line segment from ( − 7 , 9 ) (−7,9) to ( 3 , − 1 ) (3,−1) that partitions the segment into a ratio of 2 to 3?
Answers
The coordinates of the point on the directed line segment from (-7, 9) to (3, -1) that partitions the segment into a ratio of 2 to 3 are (-3, 5).
To find the coordinates of the point that divides the directed line segment from (-7, 9) to (3, -1) into a ratio of 2 to 3, we can use the section formula.
Let's label the coordinates of the desired point as (x, y). According to the section formula, the x-coordinate of the point is given by:
x = (2 * 3 + 3 * (-7)) / (2 + 3) = (6 - 21) / 5 = -15 / 5 = -3
Similarly, the y-coordinate of the point is given by:
y = (2 * (-1) + 3 * 9) / (2 + 3) = (-2 + 27) / 5 = 25 / 5 = 5
Therefore, the coordinates of the point that divides the line segment in a ratio of 2 to 3 are (-3, 5).
To understand this conceptually, consider the line segment as a distance from the starting point (-7, 9) to the ending point (3, -1). The ratio of 2 to 3 means that the desired point is two-thirds of the way from the starting point and one-third of the way from the ending point. By calculating the x and y coordinates using the section formula, we find that the desired point is located at (-3, 5).
For more such questions on segment
https://brainly.com/question/280216
#SPJ8
PLEASE HELP ME!!!!!!!
A soda company would like to replace the label on a can of soda with a radius of 2 and three fourths cm. If the label touches end to end with no overlap, what is the length of the label? Use 22 over 7 for π.
121 over 7 cm
121 over 14 cm
121 over 28 cm
121 over 56 cm
Answers
According to the problem the length of the label is 121 over 28 cm.
What is label?A label is a piece of text, image, or other object used to identify and describe an item, product, or object. Labels are typically used to provide information about an item, such as its size, manufacturer, contents, or use. Labels can also be used for labeling items for sale, for labeling items for storage, or for labeling items for shipment.
The length of the label can be calculated using the circumference formula, C = π x d, where C is the circumference and d is the diameter.
The diameter of the can is 2 and three fourths cm, so the circumference is 22 over 7 x 2 and three fourths, which is equal to 121 over 7.
To get the length of the label, divide 121 over 7 by the number of labels needed - in this case, 4.
So, the length of the label is 121 over 28 cm.
To learn more about label
https://brainly.com/question/27943533
#SPJ1
GHIJK ~ STUVR. What is mZV?
R
G
1020
V
H
1220
K
1020
960
S
1229
126
T
m2 =
o
Submit
Answers
Solve all this
1) 2x-8=11x-10
2)6x-6=3x+1
3)1/2x+4=1/3x+1
4)-2/5x+1/3=1/2x+1/4
5)5/3x2=1/2x-2/3
Answers
Answer: hii :)
1. 2x-8=11x-10 = 2/9
2. 6x-6=3x+1 = 7/3
3. 1/2x+4=1/3x+1 = -18
4. -2/5x+1/3=1/2x+1/4 = 5/54
5. I dont know the answer to <3
Step-by-step explanation:
Hopefully this helps you,
Sorry for being late on the question.
- Matthew
what number is 1/2% of 96? round the answer to the nearest hundredth if necessary.
Answers
1/2% is read as 1.2 out of one hundred
so divide 100/1.2 which the answer would be 83.33333333 or 83.3
On the SAT exam a total of 25 minutes is allotted for students to answer 20 math questions without the use of a calculator. A guidance counselor would like to know if the students in his school are prepared to complete this portion of the exam in the timeframe allotted. To investigate, the counselor selects a random sample of 35 students and administers this portion of the test. The students are instructed to turn in their test as soon as they have completed the questions. The mean amount of time taken by the students is 23.5 minutes with a standard deviation of 4.8 minutes. The counselor would like to know if the data provide convincing evidence that the true mean amount of time needed for all students of this school to complete this portion of the test is less than 25 minutes and therefore tests the hypotheses H0: μ = 25 versus Ha: μ < 25, where μ = the true mean amount of time needed by students at this school to complete this portion of the exam. The conditions for inference are met. What are the appropriate test statistic and P-value?
Answers
The P-value is between 0.025 and 0.05. and t = -1.85
On the SAT exam a total of 25 minutes is allotted for students to answer 20 math questions without the use of a calculator.
Therefore tests the hypotheses:
\(H_0\) : μ = 25 versus Ha: μ < 25,
where μ = the true mean amount of time needed by students at this school to complete this portion of the exam.
The alternative hypothesis is:
\(H_1:\mu < 25\)
The test statistic is given by:
\(t=\frac{x-\mu}{\frac{s}{\sqrt{n} } }\)
The parameters are:
'x' is the sample mean. \(\mu\) is the value tested at the null hypothesis.s is the standard deviation of the sample.n is the sample size.the values of the parameters are:
x = 23.5 , \(\mu=25\) , s = 4.8, n = 35
Plug all the values in above formula of t- statistic is:
\(t = \frac{23.5-25}{\frac{4.8}{\sqrt{35} } }\)
t = -1.85
Using a t-distribution , with a left-tailed test, as we are testing if the mean is less than a value and 35 - 1 = 34 df, the p-value is of 0.0365.
t = –1.85; the P-value is between 0.025 and 0.05.
Learn more about t-distribution at:
https://brainly.com/question/13574945
#SPJ1
at football practice, gustavo does push ups for 2 minutes for every 6 minutes playing if he plays for 42 minutes how many of push ups will he do
Answers
Answer:
14 mins
Step-by-step explanation:
2/6 = x/42
6x=84
x=14
some adults and children are watching a musical there are n children there are 25 fewer adults
Answers
According to the concept of algebraic expression and arithmetic, the correct answers are A) Number of adults = N - 25. B) Number of adults when N = 124: 124 - 25 = 99
A) Let's denote the number of children as N. Since there are 25 fewer adults than children, the number of adults can be expressed as N - 25.
B) If there are 124 children, we substitute N with 124 in the expression from part A. Thus, the number of adults would be 124 - 25 = 99.
To arrive at these answers, we used the given information that there are "N" children and 25 fewer adults than children. By substituting the value of N, we determined the number of adults in terms of N and then calculated the specific number of adults when N is equal to 124.
Note: The given question is incomplete. The complete question is:
Some adults and children are watching a musical. there are 'N' number of children. There are 25 fewer adults than children.
A) find the number of adults in terms of 'N'.
B) if there are 124 children how many adults are there?
For more questions on algebraic expression:
https://brainly.com/question/29333936
#SPJ8
how do I subtract 45 1/3 - 9 3/5
Answers
Answer:
35.733
Step-by-step explanation:
have a common denominator then do the math
The ratio 5 to 6 represents the number of salty snacks to sweet snacks people buy in a day at a store. a. If the store sold 36 sweet snacks, how many salty snacks did they sell? Prove your answer b. If the store sold 50 salty snacks, how many sweet snacks did they sell? Prove your answe
Answers
Answer:
give me tha answer please
In the diagram a person who is ft tall is standing on the ground ft away from point . A line segment drawn from the top corner of the building to point creates two similar triangles.
Answers
The height of the building, using similar triangles, is given by:
36 feet.
What are similar triangles?Similar triangles are two triangles that share these two features, which are listed as follows:
Same angle measures.Proportional side lengths.The second bullet point, regarding proportional side lengths, is especially relevant in the context of this problem, as a proportional relationship is built to find the height h of the building.
From the similar triangles, the equivalent side lengths are presented as follows:
3 ft and 18 ft.6 ft and h ft.Hence the proportional relationship that models this situation is presented as follows:
3/18 = 6/h.
Applying cross multiplication, the height of the building is obtained as follows:
3h = 18 x 6
h = 6 x 6 (simplifying by 3)
h = 36 feet.
Missing InformationThe diagram is given by the image shown at the end of the answer.
More can be learned about similar triangles at brainly.com/question/11920446
#SPJ1

In a certain community, 8% of all adults over 50 have diabetes. If a health service in this community correctly diagnoses 95% of all persons with diabetes as having the disease and incorrectly diagnoses 2% of all persons without diabetes as having the disease, find the probabilities that
a) the community health service will diagnose an adult over 50 as having diabetes.
b) a person over 50 diagnosed by the health service as having diabetes actually has the disease.
Answers
Answer and Step-by-step explanation:
Solution:
Given:
Let A is the event of a person over 50 diagnosed by health service.
B1 is the event that an adult over 50 actually has diabetes.
B2 is the event that an adult over 50 does not have diabetes.
P (B1) = 8% = 0.08
And P (B2) = 1 – P (B1)
= 1 – 0.08
= 0.92
Correctly diagnose of all persons with diabetes= 95%
P (A/B1) = 0.95
Incorrectly diagnose of all persons without diabetes= 2%
P (A/B2) = 0.02
(a) ) the community health service will diagnose an adult over 50 as having diabetes.
P (B1) P (A/B1) = (0.08) (0.95) = 0.076
P (B2) p (A/B2) = (0.92) (0.02) =0.0184
P (B1) P (A/B1) + P (B2) p (A/B2) = 0.076 + 0.0184
= 0.0944
(b) A person over 50 diagnosed by the health service as having diabetes actually has the disease.
By using formula:
P (B1/A) = P (B1) P (A/B1) / P (B1) P(A/B1) + P (B2) P (A/B2)
Put all the given values:
= (0.08) (0.95) / (0.08) (0.95) + (0.92) (0.02)
=0.076 / 0.076 + 0.0184
=0.076 / 0.0944
= 0.8050
Using conditional probability, it is found that there is a:
a) 0.0944 = 9.44% probability that the community health service will diagnose an adult over 50 as having diabetes.
b) 0.8051 = 80.51% probability that a person over 50 diagnosed by the health service as having diabetes actually has the disease.
Conditional Probability
\(P(B|A) = \frac{P(A \cap B)}{P(A)}\)
In which
P(B|A) is the probability of event B happening, given that A happened. \(P(A \cap B)\) is the probability of both A and B happening. P(A) is the probability of A happening.Item a:
The percentages of a positive test is:
95% of 8%(have diabetes).2% of 92%(do not have diabetes).Hence:
\(P(A) = 0.95(0.08) + 0.02(0.92) = 0.0944\)
0.0944 = 9.44% probability that the community health service will diagnose an adult over 50 as having diabetes.
Item b:
Event A: Positive test.Event B: Has the disease.From item a, \(P(A) = 0.0944\).
The probability of both a positive test and having the disease is:
\(P(A \cap B) = 0.95(0.08)\)
Hence, the conditional probability is:
\(P(B|A) = \frac{P(A \cap B)}{P(A)} = \frac{0.95(0.08)}{0.0944} = 0.8051\)
0.8051 = 80.51% probability that a person over 50 diagnosed by the health service as having diabetes actually has the disease.
A similar problem is given at https://brainly.com/question/14398287
2
Find the missing side of each triangle. Leave your answers in simplest radical form.

Answers
Answer: x = sqrt(10)
Step-by-step explanation:
You can use the Pythagorean Theorem to solve:
a^2 + b^2 = c^2
You are given one leg (sqrt6) and the hypotenuse (4) and are asked to solve for the other leg (x). Plugging everything into the equation, you get:
(sqrt6)^2 + b^2 = (4)^2
Now, you can solve for b:
b^2 = 4^2 - (sqrt6)^2
b^2 = 16 - 6
b^2 = 10
b = sqrt(10)
In this case, b is equivalent to x, so your answer is x = sqrt(10).
Answer:
x = √10
Step-by-step explanation:
C^2 = A^2 + B^2
4^2 = (√6)^2 + x^2
16 = 6 + x^2
x^2 = 10
x = √10
lect the correct answer.
Under which condition is the sample proportion, , a point estimate of the population proportion?
A.
The sample proportion is never a point estimate of the population proportion.
B.
The sample represents a proportion of the population.
C.
The sample proportion is unbiased.
D.
The sample size, n, is small enough.
Reset Next
Answers
The correct answer is B. The sample represents a proportion of the population.
What is the sample population ?
A point estimate is a single value used to estimate a population's unknown parameter. The sample proportion (denoted by p), in the context of determining the population proportion, is a widely used point estimate. The sample proportion is determined by dividing the sample's success rate by the sample size.
The sample must be representative of the population for it to be a reliable point estimate of the population proportion. To accurately reflect the proportions of various groups or categories present in the population, the sample should be chosen at random.
Learn more about population:https://brainly.com/question/30324262
#SPJ1
ActivityPlane A is descending toward the local airport, and plane B is ascending from the same airport. Plane A is descending at a rate of 2,500 feet perminute. Plane B is ascending at a rate of 4,000 feet per minute. If plane A is currently at an altitude of 14,000 feet and plane B is at an altitude of1,000 feet, how long will it take them to be at the same altitude? Represent time in minutes as the x-variable and altitude in thousands of feet asthe y-variable.
Answers
Let:
y1 = altitude of the plane A
y2 = altitude of the plane B
Let's find the equation for plane A:
\(\begin{gathered} m1=-2500 \\ y1=-2500x+b \\ for \\ 14000=-2500(0)+b \\ b=14000 \\ y1=-2500x+14000 \end{gathered}\)And for plane B:
\(\begin{gathered} m2=4000 \\ y2=4000x+b \\ for \\ 1000=4000(0)+b \\ b=1000 \\ y2=4000x+1000 \end{gathered}\)So:
\(\begin{gathered} y1=y2 \\ -2500x+14000=4000x+1000 \\ solve_{\text{ }}for_{\text{ }}x\colon_{} \\ 6500x=13000 \\ x=\frac{13000}{6500} \\ x=2 \end{gathered}\)Answer:
2 minutes

In September 2016, the cost of gasoline in Berlin was around 1.21 euros per liter.
What would the equivalent cost be in U.S. dollars per gallon?
1 U.S. dollar ~ 0.896 euros
1 gallon 3.785 liters
Answers
Using proportions, it is found that the equivalent cost in U.S. dollars per gallon would be of 5.11.
What is a proportion?A proportion is a fraction of total amount, and the measures are related using a rule of three.In September 2016, the cost of gasoline in Berlin was around 1.21 euros per liter. Hence, per gallon, that is, per 3.785 liters, we use a rule of three to find the cost.
1.21 euros - 1 liter
x euros - 3.785 liters
Applying cross multiplication:
\(x = 1.21(3.785) = 4.57985\)
Cost of 4.57986 euros per gallon. Since 1 U.S dollar is equivalent to approximately 0.896 euros, we have that:
1 dollar - 0.896 euros
x dollars - 4.57986 euros
Applying cross multiplication again:
\(0.896x = 4.57986\)
\(x = \frac{4.57986}{0.896}\)
\(x = 5.11\)
The equivalent cost in U.S. dollars per gallon would be of 5.11.
You can learn more about proportions at https://brainly.com/question/24372153
I have 0 idea what this even means? Does anyone know the answer and if you could possibly elaborate if you do? Very confused over here
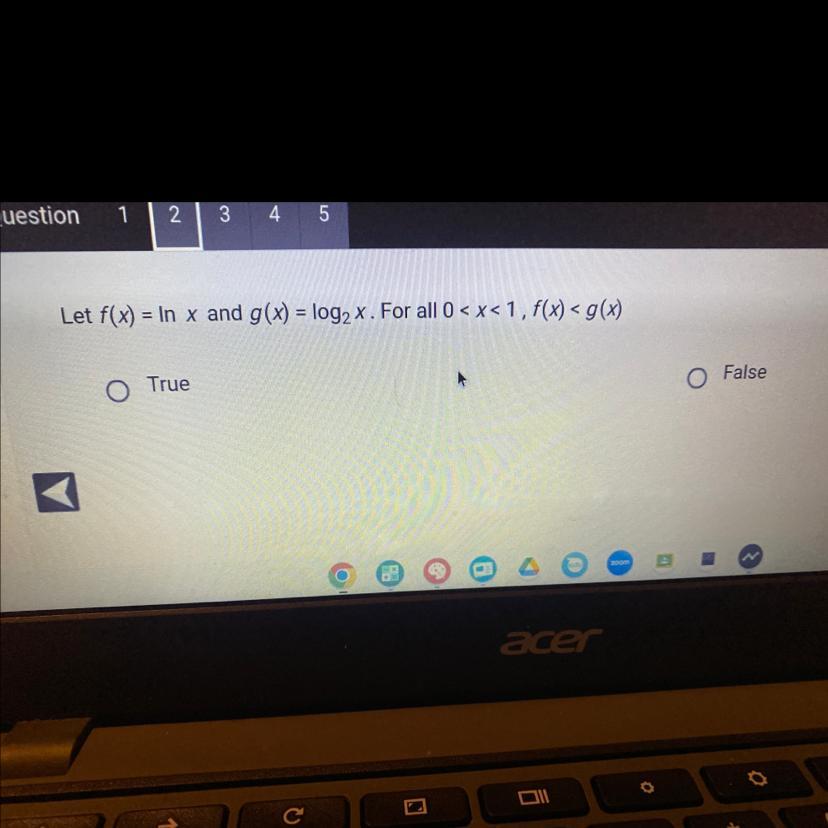
Answers
Let f(x) = lnx and g(x) = log₂x. for all 0 < x < 1, f(x) < g(x): True.
How to determine the corresponding output value for this function?In this scenario and exercise, we would determine the corresponding output value for the functions f(x) and g(x) under the given mathematical operation and independent variables.
When x = 1, the output value for f(x) based on the table of values is given by;
f(x) = lnx
f(1) = ln(1).
f(1) = 0.
When x = 2, the output value for f(x) based on the table of values is given by;
f(x) = lnx
f(2) = ln(2).
f(2) = 0.69314718
When x = 1, the output value for g(x) based on the table of values is given by;
g(x) = log₂x
g(1) = log₂(1)
g(1) = 0.
When x = 2, the output value for g(x) based on the table of values is given by;
g(x) = log₂x
g(2) = log₂(2)
g(2) = 1.
In this context, we can logically deduce that the function f(x) is less than function g(x) for all 0 < x < 1.
Read more on function here: brainly.com/question/10687170
#SPJ1
Does the graph represent a function? Why or why not ?

Answers
Answer:
A.
Step-by-step explanation:
The vertical line test is a way of finding out if a relation is a function.
Graph the relation.
Then imagine a vertical line moving from left to right over the graph of the relation.
If the vertical line intersects at most one point of the graph in any position you place the vertical line, then the relation is a function.
This function passes the vertical test since it never intersects more than one point on the vertical line at a time.
Answer: A.
Jim walks 6/7 of a mile every day. Russell walks 1/4 of a mile. How much farther does Jim work than Russell.
Answers
Answer:
Jim walked 17/28 for miles than Russel
Step-by-step explanation:
First you turn 6/7 and 1/4 to have the same denominators. In that case you find the least common multiple which is 28.
7: 7, 14, 21, 28
4: 4, 8, 12, 16, 20, 24, 28
Next you multiply the top and the bottom of your fraction my the factor you used to get 28 for your denominator
6/7 x 4/4 = 24/28
1/4 x 7/7 = 7/28
Lastly, you subtract the products you got.
24/28 - 7/28 = 17/28