If the temperature is 20c what is it in Fahrenheit.
Answers
Answer:
The answer is 68 degrees Fahrenheit.
Step-by-step explanation:
The equation to convert Celsius to Fahrenheit is (C × 9/5) + 32.
So, first we calculate Celsius times 9/5. 20×9/5 = 36.
Then, we add 36 and 32 together. 36+32= 68
So, 68 is your answer.
Related Questions
Determine whether each expression is equivalent to 100t^2-0.5t

Answers
Answer:
\(100^{t^{2}-0.5\cdot t}\) is not equivalent to \(\frac{10^{t^{2}}}{100^{t}}\).
\(100^{t^{2}-0.5\cdot t}\) is not equivalent to \(\frac{50^{t^{2}}\cdot 2^{t^{2}}}{25^{0.5\cdot t}\cdot 4^{0.5\cdot t}}\).
\(100^{t^{2}-0.5\cdot t}\) is not equivalent to \(\frac{50^{t^{2}-0.5\cdot t}}{5^{t^{2}-0.5\cdot t}}\).
Step-by-step explanation:
The expression to be evaluated is \(100^{t^{2}-0.5\cdot t}\), we find by algebraic means the equivalent expression:
Possibility 1:
\(100^{t^{2}-0.5\cdot t}\)
\(\frac{100^{t^{2}}}{100^{0.5\cdot t}}\)
\(\frac{100^{t^{2}}}{(100^{0.5})^{t}}\)
\(\frac{100^{t^{2}}}{10^{t}}\)
\(100^{t^{2}-0.5\cdot t}\) is not equivalent to \(\frac{10^{t^{2}}}{100^{t}}\).
Possibility 2:
\(100^{t^{2}-0.5\cdot t}\)
\(\frac{100^{t^{2}}}{100^{0.5\cdot t}}\)
\(\frac{(50\cdot 2)^{t^{2}}}{(25\cdot 4)^{0.5\cdot t}}\)
\(\frac{50^{t^{2}}\cdot 2^{t^{2}}}{25^{0.5\cdot t}\cdot 4^{0.5\cdot t}}\)
\(100^{t^{2}-0.5\cdot t}\) is not equivalent to \(\frac{50^{t^{2}}\cdot 2^{t^{2}}}{25^{0.5\cdot t}\cdot 4^{0.5\cdot t}}\).
Possibility 3:
\(100^{t^{2}-0.5\cdot t}\)
\(\left(\frac{500}{5} \right)^{t^{2}-0.5\cdot t}\)
\(\frac{500^{t^{2}-0.5\cdot t}}{5^{t^{2}-0.5\cdot t}}\)
\(100^{t^{2}-0.5\cdot t}\) is not equivalent to \(\frac{50^{t^{2}-0.5\cdot t}}{5^{t^{2}-0.5\cdot t}}\).
help pls
1
3
144
432
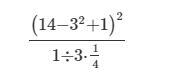
Answers
The value of the given equation is 12.
What is the value of the equation?In order to solve this question, the BODMAS rule would be used. The BODMAS rule gives the order in which mathematical operations can be solved. The order is:
Bracket OfDivision Multiplication Addition SubtractionIn the numerator:
the addition would be done first: 3² + 1 = 9 + 1 = 10
Then the subtraction would be done next = 14 - 10 = 4
Now determine the square of the term in the bracket : 4²= 16
In the denominator:
The multiplication would be solved first: 3 x 1/4 = 3/4
The next step is to solve the division : 1 ÷ 3/4 = 1 x 4/3 = 4/3
The fraction becomes : 16 ÷ 4/3
16 x 3/4 = 12
To learn more about multiplication, please check: https://brainly.com/question/3385014
#SPJ1
Answer:
The answer is 432
Step-by-step explanation:
I did the k 12 quiz and I got it right! good luck
Calculate ∫(4(x²−y)⃗ +5(y²+x)⃗ ) ⋅ ⃗ if
(a) C is the circle (x−8)²+(y−2)² = 16 oriented counterclockwise.
∫(4(x²−y)⃗ + 5(y²+x)⃗ )⋅⃗ = ______
(b) C is the circle (x−)²+(y−)² = ² in the xyxy-plane oriented counterclockwise.
∫(4(x²−y)⃗ +5(y²+x)⃗ )⋅⃗ = _____
Answers
(a) To calculate the line integral ∫(4(x²−y)⃗ + 5(y²+x)⃗ )⋅⃗ over the circle C given by (x−8)²+(y−2)² = 16 oriented counterclockwise, we need to parametrize the curve C. The parametric equations for a circle of radius 4 centered at (8, 2) can be written as x = 8 + 4cos(t) and y = 2 + 4sin(t), where t ranges from 0 to 2π.
Substituting these expressions into the integrand and evaluating the dot product, we have:
∫(4(x²−y)⃗ + 5(y²+x)⃗ )⋅⃗ = ∫(4(8 + 4cos(t))² - (2 + 4sin(t)))dx + 5((2 + 4sin(t))² + (8 + 4cos(t)))dy.
Using the parametric equations and differentiating with respect to t, we can express dx and dy in terms of dt:
dx = -4sin(t)dt,
dy = 4cos(t)dt.
Substituting these expressions into the integral, we get:
∫(4(x²−y)⃗ + 5(y²+x)⃗ )⋅⃗ = ∫(4(8 + 4cos(t))² - (2 + 4sin(t)))(-4sin(t))dt + 5((2 + 4sin(t))² + (8 + 4cos(t)))(4cos(t))dt.
Integrating with respect to t over the range 0 to 2π, we can evaluate the integral to obtain the final answer.
(b) To calculate the line integral ∫(4(x²−y)⃗ + 5(y²+x)⃗ )⋅⃗ over the circle C given by (x−a)²+(y−b)² = r² in the xy-plane oriented counterclockwise, we need the specific values for a, b, and r. Please provide the values for a, b, and r in order to proceed with the calculation.
To learn more about brainly.com/question/29275326#SAPJ11
Consider a fractal line with fractal dimension D. The mean-square distance between monomers u and v along this line is ⟨(R(u)−R(v))2⟩=b2(v−u)2/D. Calculate the mean-square end-to-end distance R2 and radius of gyration Rg2 for this fractal line. Determine the ratio R2/Rg2 symbolically and then calculate this ratio for fractal dimensions D=1,1.7 and 2 .
Answers
The mean-square end-to-end distance for the fractal line is ⟨R2⟩ = b².L^(1-D).
The mean-square end-to-end distance for the fractal line is as follows.⟨R2⟩ = ⟨(R(u)- R(v))^2⟩ for u = 0 and v = L where L is the length of the line.⟨R2⟩ = b²/L^2.D.L = b².L^(1-D).
Thus, the mean-square end-to-end distance for the fractal line is ⟨R2⟩ = b².L^(1-D).
The radius of gyration Rg is defined as follows.
Rg² = (1/N)∑_(i=1)^N▒〖(R(i)-R(mean))〗²where N is the number of monomers in the fractal line and R(i) is the position vector of the ith monomer.
R(mean) is the mean position vector of all monomers.
Since the fractal dimension is D, the number of monomers varies with the length of the line as follows.N ~ L^(D).
Therefore, the radius of gyration for the fractal line is Rg² = (1/L^D)∫_0^L▒〖(b/v^(1-D))^2 v dv〗 = b²/L^2.D(1-D). Thus, Rg² = b².L^(2-D).
The ratio R²/Rg² is given by R²/Rg² = L^(D-2).
When D = 1, R²/Rg² = 1/L. When D = 1.7, R²/Rg² = 1/L^0.7. When D = 2, R²/Rg² = 1/L.
This provides information on mean-square end-to-end distance and radius of gyration for fractal line with a given fractal dimension.
Learn more about mean-square from the given link
https://brainly.com/question/30763770
#SPJ11
The measure of angle DBE is (0.2 - 32) and the measure of angle CBE is (0.2 - 42) . Find the value of x.
Please answer quick! Im begging!

Answers
The value of x for the given angles will be x= 50.
What is geometry?The study of the figures like square, rectangle circle and their angles is called as geometry.
We know that the sum of the angles in a triangle is 180 degrees. Therefore, we can write:
∠CBE + ∠DBE + angle EBC = 180
Substituting the given expressions for angle CBE and angle DBE, we get:
(0.2x - 42) + (0.2x - 32) + angle EBC = 180
Simplifying the left side of the equation, we get:
0.4x - 74 + angle EBC = 180
Adding 74 to both sides, we get:
0.4x + angle EBC = 254
We know that angle EBC is supplementary to both angle CBE and angle DBE since they form a straight line. Therefore, we can write:
∠CBE + ∠EBC = 180
∠DBE + ∠EBC = 180
Substituting the expression (0.2x - 42) for angle CBE and the expression (0.2x - 32) for angle DBE, we get:
(0.2x - 42) + angle EBC = 180
(0.2x - 32) + angle EBC = 180
Simplifying each equation, we get:
∠EBC = 222 - 0.2x (1)
∠EBC = 212 - 0.2x (2)
Setting the right sides of equations (1) and (2) equal to each other, we get:
222 - 0.2x = 212 - 0.2x
Simplifying and solving for x, we get:
10 = 0.2x
x = 50
Therefore, the value of x is 50.
To know more about geometry follow
https://brainly.com/question/23925137
#SPJ1
Nine friends vote on their favorite fruit. only one person in the group votes for kiwi. choose the decimal that is equivalent to the fraction of friends who vote for kiwi. group of answer choices
Answers
The decimal equivalent to the fraction of friends who vote for kiwi is 0.111.
In the given scenario, nine friends have voted on their favorite fruit, and only one person in the group voted for kiwi. We are tasked with finding the decimal equivalent of the fraction representing the friends who voted for kiwi.
To determine the decimal equivalent, we need to calculate the fraction and then convert it into decimal form. In this case, the fraction representing the friends who voted for kiwi is 1 out of 9, or 1/9.
To convert this fraction into a decimal, we divide the numerator (1) by the denominator (9):
1 ÷ 9 = 0.1111...
The decimal representation of 1/9 is 0.1111..., where the digit 1 repeats infinitely.
The decimal 0.1111... is an example of a recurring decimal, which means it repeats the same pattern of digits indefinitely. In this case, the digit 1 repeats endlessly. When we write it in decimal form, we typically use the ellipsis (...) to indicate the recurring pattern.
Therefore, the decimal equivalent to the fraction of friends who voted for kiwi is 0.1111..., where the digit 1 repeats indefinitely.
It is important to note that when working with decimals, we can approximate recurring decimals by rounding to a certain number of decimal places. However, in this case, since the pattern of 1s repeats indefinitely, it cannot be precisely represented in a finite number of decimal places.
In summary, the decimal equivalent of the fraction representing the friends who voted for kiwi is 0.1111..., where the digit 1 repeats indefinitely.
Learn more about fraction here
https://brainly.com/question/30154928
#SPJ11
At a real estate agency, an agent sold a house for $397,000. The commission rate is 4.5% for the real estate agency and the commission rate for the agent is 20% of the amount the real estate agency gets. How much did the agency make on the house? How much did the agent earn in commission?
Answers
Answer:
1. $97,265
2. $17,865
Step-by-step explanation:
Step one:
given data
cost of the house= $397,000.
we are told that the commission is 4.5% real estate agency
and also the agent commission is 20%
Step two:
1. How much did the agency make on the house?
this amount is 20% plus 4.5% together.
=20/100*397,000 +4.5/100*397,000
=0.2*397,000. +0.045*397,000.
=79400+17865
=97,265
The agent made a total of $97,265 on the house
2. How much did the agent earn in commission?
in commission, the rate is 4.5% which amounts to $17,865
a stock has an expected return of 10.5 percent, its beta is 1.00, and the risk-free rate is 6.25 percent. what must the expected return on the market be? (do not round intermediate calculations and enter your answer as a percent rounded to 2 decimal places, e.g., 32.16.) market expected return %
Answers
The expected return on the market must be 10.5 percent, according to the given values.
Expected return is a measure used in finance to calculate the average return an investment is expected to generate over a specific period. It is a weighted average of the possible returns, where each return is multiplied by its respective probability.
The expected return on a stock can be determined using the capital asset pricing model (CAPM), which relates the expected return of an asset to its beta and the expected return of the market. The formula for the CAPM is as follows:
Expected Return = Risk-Free Rate + Beta * (Market Expected Return - Risk-Free Rate). In this case, the stock has an expected return of 10.5 percent, a beta of 1.00, and the risk-free rate is 6.25 percent. Let's denote the market expected return as "M."
Plugging in the values into the CAPM formula: 10.5% = 6.25% + 1.00 * (M - 6.25%).
Simplifying the equation:
10.5% - 6.25% = M - 6.25%
4.25% = M - 6.25%
M = 4.25% + 6.25%
M = 10.5%
Therefore, the expected return on the market must be 10.5 percent in order to be consistent with the given information.
To know more about returns, refer here :
https://brainly.com/question/29730147#
#SPJ11
What is the value of x?

Answers
Answer:
48 degrees.
Step-by-step explanation:
The value of a triangle equals 180* in total, so, 47 + 85 = 132.
180-132=48*.
$......
(c) One month, Gretal spent a total of $360 on presents.
She spent 1/5 of this total on presents for her parents.
She spent 2/3of the remaining money on presents for her friends.
She spent the rest of the money on presents for her sisters.
Calculate the percentage of the $360 that she spent on presents for her sisters.
Answers
The percentage that she spent on present for her sister is 26.67%
What does % example mean?
Since one percent (symbolized as 1%) is equal to one hundredth of something, 100 percent stands for everything, and 200 percent refers to twice the amount specified. As an illustration, 1% of 1,000 chickens is equal to 1/100 of 1,000, or 10 birds, and 20% of the quantity is equal to 20% of 1,000, or 200.
Given that :
She spent = 360 * 1/5 = $72 on presents for her parents
she spent = 360 - 72 = 288 * 2/3 = $192 on presents for her friends
She spent = 288 - 192 = $96 on presents for her sister
Percentage of the $360 that she spent on presents for her sisters is
96/360 * 100 = 26.67%
Hence the percentage that she spent on present for her sister is 26.67%
Learn more about percentages
https://brainly.com/question/24877689
#SPJ1
Solve the following equation for x: 8x^2 + 6x = -5
Answers
Answer:
\(\mathrm{The\:solutions\:to\:the\:quadratic\:equation\:are:}\)
\(x=-\frac{3}{8}+i\frac{\sqrt{31}}{8},\:x=-\frac{3}{8}-i\frac{\sqrt{31}}{8}\)
Step-by-step explanation:
\(8x^2+6x=-5\)
\(\mathrm{Add\:}5\mathrm{\:to\:both\:sides}\)
\(8x^2+6x+5=-5+5\)
\(8x^2+6x+5=0\)
\(\underline{\mathrm{Solve\: further\:using\:the\:quadratic\: formula}}\)
\(x_{1,\:2}=\frac{-6\pm \sqrt{6^2-4\cdot \:8\cdot \:5}}{2\cdot \:8}\)
\(x_{1,\:2}=\frac{-6\pm \:2\sqrt{31}i}{2\cdot \:8}\)
\(\mathrm{Separate\:the\:solutions}\)
\(x_1=\frac{-6+2\sqrt{31}i}{2\cdot \:8},\:x_2=\frac{-6-2\sqrt{31}i}{2\cdot \:8}\)
\(\bold{\frac{-6+2\sqrt{31}i}{2\cdot \:8}=-\frac{3}{8}+\frac{\sqrt{31}}{8}i}\)
\(\bold{\frac{-6-2\sqrt{31}i}{2\cdot \:8}=-\frac{3}{8}-\frac{\sqrt{31}}{8}i}\)
More information
Quadratic equation formula:
\(\mathrm{For\:a\:quadratic\:equation\:of\:the\:form\:}ax^2+bx+c=0\mathrm{\:the\:solutions\:are\:}\)
\(x_{1,\:2}=\frac{-b\pm \sqrt{b^2-4ac}}{2a}\)
the lengths of pregnancies of humans are normally distributed with a mean of 268 days and a standard deviation of 15 days. a baby is premature if it is born three weeks early. what percent of babies are born prematurely?
Answers
8.08 percent of babies are born prematurely .
We have following information,
lengths of pregnancy of humans are Normally distributed.
mean of distribution ( μ ) = 268 days
standard deviations of distribution = 15 days
We shall find out the pecent of babies are born. prematurely.
Using the Normal distribution formula ,
Z = ( X - μ ) /σ
where X---> sample mean
μ --> poplution mean
putting the possble values of variables we get,
if a baby born three weaks early then he is considered as premature.
X = 21 , μ = 268 , r =
Z = ( 21-268)/ 15 = - 247/15 = - 16.4
Now, p-value corresponding to Z-value= -16.4 is
8.08..
thus for z= -16.4 , p-value will be 8.08 .. So, 8.08 percent of babies are born prematurely.
To learn more about Normal distribution, refer :
https://brainly.com/question/28059926
#SPJ4
If we had a Pyramid with a hexagonal base, how many of these pyramids would it take to fill up a hexagonal Prism with a congruent base, and equal height?
Answers
Answer:
3 of the pyramids
Step-by-step explanation:
Given:
Hexagonal Prism
Hexagonal based pyramid
Required
How many of the pyramid will fill up the prism
To do this, we start by calculating the volumes of both shapes.
Let V1 be the volume of the hexagonal prism
\(V_1 = \frac{3\sqrt{3}}{2}a^2h\)
Where: a = base and h = height
Let V2 be the volume of the hexagonal based pyramid
\(V_2 = \frac{\sqrt{3}}{2}a^2h\)
Where: a = base and h = height
The number of the pyramid that can occupy the prism is calculated by dividing V1 by V2
\(Number = \frac{V_1}{V_2}\)
\(Number = \frac{3\sqrt{3}}{2}a^2h /\frac{\sqrt{3}}{2}a^2h\)
Convert division to multiplication
\(Number = \frac{3\sqrt{3}}{2}a^2h * \frac{2}{\sqrt{3}a^2h}\)
\(Number = \frac{3\sqrt{3}}{2} * \frac{2}{\sqrt{3}}\)
\(Number = \frac{3\sqrt{3}}{1} * \frac{1}{\sqrt{3}}\)
\(Number = \frac{3*1}{1} * \frac{1}{1}\)
\(Number = 3\)
How do you find the trapezoidal rule?
Answers
To find the trapezoidal rule, you must integrate the function with the trapezoidal rule formula.
The trapezoidal rule is a numerical integration method used to approximate the definite integral of a function. It is a simple and popular method of approximating definite integrals, especially when the function is not easy to integrate analytically.
The trapezoidal rule estimates the definite integral by dividing the area under the curve into a series of trapezoids, and then summing the areas of these trapezoids.
The formula for the trapezoidal rule is: (b-a) * (f(a) + f(b)) / 2
Where a and b are the limits of integration, f(a) and f(b) are the function evaluated at the limits of integration and (b-a) is the width of the trapezoid.
In practice, to find the trapezoidal rule, you must divide the definite integral into small subintervals and then evaluate the function at the endpoints of each subinterval.
Then you can use the trapezoidal rule formula to find the approximate area under the curve by summing the areas of all the trapezoids. It's important to note that the more subintervals you use, the more accurate the approximation will be.
To know more about trapezoidal rule click on the link below:
https://brainly.com/question/17218343#
#SPJ11
Work out angle BXC, give reasons for all angles you work out

Answers
The value of Angle BXC is 70°
What are corresponding angles?Corresponding angles are the angles which are formed in matching corners with the transversal when two parallel lines are intersected by any other line called the transversal.
The line which joins the two parallel lines is usually called a transversal.
Angle XBC is 55° because it is corresponding with Angle AXY
From triangle XBC, Angle XBC is equal to XCB( base angles of an isosceles triangle)
so XBC = XCB = 55°
Also,
XBC + XCB + BXC = 180( sum of angles in triangle XBC)
55 + 55 + BXC = 180
110 + BXC = 180
BXC = 180 - 110
BXC = 70°
In conclusion, Angle BXC is 70°
Learn more about corresponding angles: https://brainly.com/question/22190474
#SPJ1
The perimeter of a square is 80 minus 64 y units. Which expression can be used to show the side length of one side of the square?
16 (5 minus 4 y): Each side measures 5 minus 4 y units.
16 y (5 minus 4): Each side measures 5 minus 4 units.
4 (20 minus 16 y): Each side measures 20 minus 16 y units.
4 y (20 minus 16): Each side measures 20 minus 16 units.
Answers
The expression that represents the side length of the square is as follows:
(20 minus 16 y): Each side measures 20 minus 16 y units.How to find the side length of a square?A square is a quadrilateral with 4 sides equal to each other. The opposite sides are parallel to each other. The sum of angles in a square is 360 degrees. Each angle in the square is 90 degrees.
The sum of the whole side of a square is the perimeter of the square.
Therefore, the perimeter of the square is 80 minus 64 y units.
Let's use expression to find the side length as follows;
perimeter of a square = 4l
where
l = side lengthTherefore,
80 - 64y = 4l
divide both sides of the equation by 4
l = 80 / 4 - 64y / 4
l = 20 - 16y
Therefore,
side length = 20 - 16y
learn more on square here: https://brainly.com/question/17087381
#SPJ1
Answer:
yo
Step-by-step explanation:
the answer is C
true or false? in the context of our theory of inductive proofs, p(n) represents the quantity about which we are proving something.
Answers
In the context of our theory of inductive proofs, P(n) represents the quantity about which we are proving something- False.
A proof by induction requires justification at every step, just like a regular proof. But, it uses a clever technique that enables you to demonstrate the truth of a proposition when n is 1, assume it is true for n=k, and then demonstrate that it is true for n=k+1.
According to the theory, all that is required to demonstrate a person's ability to ascend to the nth floor of a fire escape is for them to demonstrate their ability to ascend the fire escape ladder (n=1) and their ability to ascend the stairs from any level of the fire escape (n=k) to the next level (n=k+1).
You could have been asked to assume the n-1 case and prove the n case if you've done proof by induction before, or to assume the n case and show the n+1 case. This is the same as what I'm describing here, but I'll use a different letter since I believe it helps people understand what each instance is for better.
Learn more about Inductive proofs:
https://brainly.com/question/30474602
#SPJ4
An equation for the graph shown to the right is: 4 y=x²(x-3) C. y=x²(x-3)³ b. y=x(x-3)) d. y=-x²(x-3)³ 4. The graph of the function y=x¹ is transformed to the graph of the function y=-[2(x + 3)]* + 1 by a. a vertical stretch by a factor of 2, a reflection in the x-axis, a translation of 3 units to the right, and a translation of 1 unit up b. a horizontal stretch by a factor of 2, a reflection in the x-axis, a translation of 3 units to the right, and a translation of 1 unit up c. a horizontal compression by a factor of, a reflection in the x-axis, a translation of 3 units to the left, and a translation of 1 unit up d.a horizontal compression by a factor of, a reflection in the x-axis, a translation of 3 units to the right, and a translation of 1 unit up 5. State the equation of f(x) if D = (x = Rx) and the y-intercept is (0.-). 2x+1 x-1 x+1 f(x) a. b. d. f(x) = 3x+2 2x + 1 3x + 2 - 3x-2 3x-2 6. Use your calculator to determine the value of csc 0.71, to three decimal places. b. a. 0.652 1.534 C. 0.012 d. - 80.700
Answers
The value of `csc 0.71` to three decimal places is `1.534` which is option A.
The equation for the graph shown in the right is `y=x²(x-3)` which is option C.The graph of the function `y=x¹` is transformed to the graph of the function `y=
-[2(x + 3)]* + 1`
by a vertical stretch by a factor of 2, a reflection in the x-axis, a translation of 3 units to the right, and a translation of 1 unit up which is option A.
The equation of `f(x)` if `D = (x = Rx)` and the y-intercept is `(0,-2)` is `
f(x) = 2x + 1`
which is option B.
The value of `csc 0.71` to three decimal places is `1.534` which is option A.4. Given a graph, we can find the equation of the graph using its intercepts, turning points and point-slope formula of a straight line.
The graph shown on the right has the equation of `
y=x²(x-3)`
which is option C.5.
The graph of `y=x¹` is a straight line passing through the origin with a slope of `1`. The given function `
y=-[2(x + 3)]* + 1`
is a transformation of `y=x¹` by a vertical stretch by a factor of 2, a reflection in the x-axis, a translation of 3 units to the right, and a translation of 1 unit up.
So, the correct option is A as a vertical stretch is a stretch or shrink in the y-direction which multiplies all the y-values by a constant.
This transforms a horizontal line into a vertical line or a vertical line into a taller or shorter vertical line.6.
The function is given as `f(x)` where `D = (x = Rx)` and the y-intercept is `(0,-2)`. The y-intercept is a point on the y-axis, i.e., the value of x is `0` at this point. At this point, the value of `f(x)` is `-2`. Hence, the equation of `f(x)` is `y = mx + c` where `c = -2`.
To find the value of `m`, substitute the values of `(x, y)` from `(0,-2)` into the equation. We get `-2 = m(0) - 2`. Thus, `m = 2`.
Therefore, the equation of `f(x)` is `
f(x) = 2x + 1`
which is option B.7. `csc(0.71)` is equal to `1/sin(0.71)`. Using a calculator, we can find that `sin(0.71) = 0.649`.
Thus, `csc(0.71) = 1/sin(0.71) = 1/0.649 = 1.534` to three decimal places. Hence, the correct option is A.
To know more about slope visit:
brainly.com/question/3605446
#SPJ11
if my avg is a 96 and my final exam is a 75 which is 25% of my whole grade what will my final grade be
Answers
Step-by-step explanation:
That means the 96 is 75% of your grade
96 (.75) + 75 (.25) = 90.75 final grade
If f(x) = x4 âÂ’ x3 x2 and g(x) = âÂ’x2, where x ≠0, what is (f â„g)(x)?.
Answers
The composite function is \(f\circ g(x) = x^8+x^6+x^4\)
Given that \(f(x)=x^4+x^3+x^2\) and \(g(x)=x^2\).
We need to calculate \(f\circ g(x)\) which is a composite function.
If two functions are given and we create another function by using the given functions, then the new function is called composite function.
So to calculate the composite function, put the value of \(g(x) = x^2\) in the function \(f(x)\).
\(f\circ g(x) = (x^2)^4+(x^2)^3+(x^2)^2\)
\(f\circ g(x) = x^8+x^6+x^4\)
Hence the composite function is \(f\circ g(x) = x^8+x^6+x^4\).
For more details, follow the link given below.
https://brainly.com/question/17299449.
The Radius of a circle is 4 millimeters. What is the circle’s area ?
Answers
Answer:
Step-by-step explanation:
S = \(R^{2} *\pi\)
S = \(4^{2} * \pi\)
S = 16 * 3,14
S = 50,24
what would this be??

Answers
what is the equation of the line in slope-intercept form?

Answers
The linear function for this problem is defined as follows:
y = x + 50.
How to define a linear function?The slope-intercept equation for a linear function is presented as follows:
y = mx + b
In which:
m is the slope.b is the y-intercept.The graph touches the y-axis at y = 50, hence the intercept b is given as follows:
b = 50.
When x increases by 10, y also increases by 10, hence the slope m is given as follows:
m = 10/10
m = 1.
Hence the function is given as follows:
y = x + 50.
More can be learned about linear functions at https://brainly.com/question/15602982
#SPJ1
Find the value of x.

Answers
35-5= 30
5x=30
30/5= 6
X=6
I think it is an acute triangle
Not positive on the type of triangle
Answer the question below. *
1 point
What is the equation of a line passes through the point (12,-48) and is perpendicular to the line
y = ²x +15?
Answers
The equation of the line perpendicular to y = 2x + 15 and passing through the point (12, -48) is y = -1/2x - 42.
To find the equation of the line passing through the point (12, -48) and perpendicular to y = 2x + 15, we need to first find the slope of the perpendicular line. The slope of the given line is 2. Since perpendicular lines have slopes that are negative reciprocals, the slope of the perpendicular line is -1/2.
Now, we use the point-slope form of the equation for a line: y - y1 = m(x - x1), where m is the slope and (x1, y1) is the given point.
Plug in the values: y - (-48) = -1/2 (x - 12)
Simplify the equation:
y + 48 = -1/2x + 6
Now, write the equation in the slope-intercept form (y = mx + b):
y = -1/2x + 6 - 48
y = -1/2x - 42
To know more about the point-slope form, click here;
https://brainly.com/question/29503162
#SPJ11
2/5 ÷ 1/6 I need the answer step by step the reciprocal kfc and da answer
Answers
\(\frac{12}{5}\) or \(2 \frac{2}{5\\}\)
Step-by-step explanation:You follow KCF (Keep Change Flip)Keep \(\frac{2}{5}\) the same
change the division sign to multiplication \(\frac{2}{5} \\\) × \(\frac{1}{6\\}\)
Flip \(\frac{1}{6}\) so that the denominator is on top and the numerator is on the bottom like this \(\frac{6}{1\\}\)
After doing those steps your new equation will look like this- \(\frac{2}{5}\) × \(\frac{6}{1}\)
Multiplying\(\frac{2}{5}\) × \(\frac{6}{1}\) Now all you have to do is multiply
1st- multiply 2x6
2nd- multiply 5x1
\(\frac{2}{5}\) × \(\frac{6}{1\\\\}\) = \(\frac{12}{5}\)
So your answer is \(\frac{12}{5\\}\) or \(2 \frac{2}{5}\)
Hope my explanation helps you out!
a research firm needs to estimate within 3% the proportion of junior executives leaving large manufacturing companies within three years. a 0.95 degree of confidence is to be used. several years ago, a study revealed that 30% of junior executives left their company within three years. to update this study, how many junior executives should be surveyed? group of answer choices 897 1,085 800 782
Answers
To estimate the proportion of junior executives leaving large manufacturing companies within three years within a 3% margin of error and a 95% confidence level, we can use the formula for sample size calculation
Thus, the research firm should survey approximately 1,085 junior executives to update the study with a 3% margin of error and a 95% confidence level Where:n = required sample sizeZ = Z-value corresponding to the desired confidence level (in this case, 0.95)p = estimated proportion from the previous study (30% or 0.3)
E = margin of error (3% or 0.03)P lugging in the values, we have:
n = (1.96^2 * 0.3 * (1 - 0.3)) / 0.03^2n ≈ 1079.68 Rounding up to the nearest whole number, the required sample size is approximately 1080. Therefore, the answer closest to this value is 1,085.
Learn more about confidence level here: brainly.com/question/31581571
#SPJ11
Can someone please help with this

Answers

An arithmetic sequence has u10 = 16 and u30 = 156.
a Find the value of 50
Answers
Answer: u50=296
Step-by-step explanation:
30-10=20
50-30=20
u30-u10=
156-16=140
u50=u30+140
u50=156+140
u50=296
help
do odds except 17

Answers
Answer:
19. 1 do 4^5 which is 1024 then do 1024^0 which is 1
21. 0.000064 do 5^-2 which is 0.04 then do 0.04^3 which is 0.000064
23. 2.33 do 9^4 which is 6561 then do 6561^-2 which is 2.32305731 so you round it to 2.33
btw you should talk to me more