If the liquid continues to cool at the same rate, what will
the temperature be at 3 PM? Explain.
Answers
The liquid's temperature decreases by -5/4°C every hour for 6 hours, resulting in a temperature change of -15/2°C. Subtracting this from the initial temperature of 0°C gives a final temperature of -15/2°C at 3 PM.
The liquid's temperature is decreasing by −5/4°C every hour. From 9 AM to 3 PM, there are six hours. Therefore, the temperature change over this period will be:
−5/4°C x 6 hours = −15/2°C
This means that the temperature will decrease by 15/2 degrees Celsius over the six-hour period. To find the final temperature at 3 PM, we need to subtract this change from the initial temperature of 0°C:
0°C - 15/2°C = -15/2°C
So the temperature of the liquid will be −15/2°C at 3 PM.
It's worth noting that this temperature is below the freezing point of water, which is 0°C, so the liquid may be frozen by this time depending on its composition.
Learn more about temperature here: brainly.com/question/29768169
#SPJ4
Complete question:
The temperature of a liquid in an experiment is 0°C at 9 AM. The experiment calls for the temperature to change −5/4°C every hour. If the liquid continues to cool at the same rate, what will the temperature be at 3 PM? Explain
Related Questions
a marketing research firm was hired to conduct a study aimed at determining the number of alcoholic drinks individuals consumed during a week's time in a metropolitan area. the firm sampled adults and asked e
Answers
A marketing research firm was hired to conduct a study on the number of alcoholic drinks consumed by individuals in a metropolitan area over a week's time. The firm would sample adults, collect data through surveys or interviews, and analyze the data to gain insights into drinking patterns in the area.
The purpose of this study is to understand the drinking patterns of individuals in the metropolitan area. By conducting this research, the marketing research firm aims to gain insights into the average number of alcoholic drinks consumed by adults in a week's time.
The firm would start by selecting a representative sample of adults from the metropolitan area. This sample should be diverse and reflect the demographics of the population.
The firm may use random sampling methods to ensure that the sample is unbiased and representative.
Once the sample is selected, the marketing research firm would then administer a survey or conduct interviews with the participants. The survey or interviews would include questions about the number of alcoholic drinks consumed by the individuals over the course of a week. The participants may be asked to provide estimates or keep a diary of their drinking habits.
After collecting the data, the marketing research firm would analyze it to determine the average number of alcoholic drinks consumed by adults in the metropolitan area during a week. They may also look for patterns or trends in the data to understand the factors that influence drinking habits.
This study aims to provide valuable information for understanding and addressing alcohol consumption in the metropolitan area.
Learn more about marketing research from the given link
https://brainly.com/question/28206725
#SPJ11
What value is equivalent to (8+2)2 + (6 − 4) × 3?
A.106
B.110
C.6
D.94
E.18
Answers
Answer:
A. 106
Step-by-step explanation:
Use the correct order of operations.
(8 + 2)² + (6 − 4) × 3 =
= 10² + 2 × 3
= 100 + 6
= 106
One repair service company charges $27 for a house call plus
$10 per hour. A different company charges $15 for a house
call plus $13 an hour. After how many hours will the price for
the service call be the same for the two companies?
Answers
Answer:
4
Step-by-step explanation:
27+10(x)
15+13(x)
27+10(4)=67
15+10(4)=67
A room that is in the shape of a cube has a capacity of 1331 cubic feet. The room is ____ feet long
Answers
Answer:
200020ft
Step-by-step explanation:
find the area of a polygon with the vertices of (-4, 5), (-1, 5), (4, -3), and (-4, -3). suggestion: plot the points on graph paper and connect the vertices to form the polygon.
Answers
The area of the polygon with the vertices (-4, 5), (-1, 5), (4, -3), and (-4, -3) is 12 square units.
To calculate the area of the polygon, we can use the shoelace formula, also known as Gauss's area formula or the surveyor's formula. The formula involves writing the x-coordinates and y-coordinates of the vertices in a specific order and performing a series of calculations.
1. We write the x-coordinates of the vertices in one row, repeating the first coordinate at the end: -4, -1, 4, -4.
2. We write the y-coordinates of the vertices in the next row, in the same order: 5, 5, -3, -3.
3. Next, we multiply each pair of adjacent x and y coordinates and add them together in a counterclockwise direction.
4. Then, we subtract the sum of the products of the y-coordinates and the x-coordinates in a counterclockwise direction.
5. Taking the absolute value of this result, we divide it by 2 to obtain the area.
Applying the shoelace formula:
Area = |((-4*5) + (-1*-3) + (4*-3) + (-4*5)) - (5*-1 + 5*4 + -3*-4 + -3*-4)| / 2
= |-49 - (-25)| / 2
= |-24| / 2
= 12 / 2
= 12.
Therefore, the area of the polygon with the given vertices is 12 square units.
To know more about area of the polygon, click here: brainly.com/question/25907039
#SPJ11
help plzzzzz! I'll give 30 points

Answers
Answer:
c
Step-by-step explanation:
Suppose J is between H and K. Use the Segment Addition Postulate to solve for x. Then find the length of each segment. If HJ=x+10 JK=9x KH=14x−58 a) Draw a sketch of the segments described above b) Write an equaation using the segment addition postulate that will help you solve the problem ___+ ___= c) combine like terms ( x terms on one side of the equal sign and numbers in the other side of the equal sign) ____ = ____ d) x= __ HJ= __ JK= __ HK= __
Answers
Answer:
x= 17
HJ= 27
JK= 153
HK= 180
Step-by-step explanation:
If HJ=x+10
JK=9x
KH=14x−58
a) The diagram of sketch of the segments described above is attached to this answer.
b) KH = HJ + JK
14x - 58 = (x + 10) + 9x
14x - 58 = x + 10 + 9x
c)
14x - 58 = x + 10 + 9x
14x - 58 = 10x + 10
Collect like terms
14x - 10x = 10 + 58
4x = 68
Divide both sides by 4
4x/4 = 68/4
x = 17
d)
x= 17
HJ= x + 10
= 17 + 10
= 27
Hence, HJ = 27
JK= 9x
= 9 × 17
= 153
Hence, JK = 153
HK=14x −58
HK = 14 × 17 - 58
= 238 - 58
= 180
Hence, HK = 180

An office manager buys 34 chairs for the new office. Each chair cost $205. What is the total amount the office manager pays for chairs?
Answers
Multiply the number of chairs by the price of the chair:
34 x 205 = 6,970
Total spent = $6,970
Justin earned $50 mowing yards and $19 washing cars. He wants to divide his money into 3 equal accounts.
How much will he put in each account? Complete the explanation.
Justin will put $
into each account.
First add $50 and $19 to find how much money Justin earned. Justin earned a total
of $
mowing yards and washing cars. Then divide the total by
to find out how much money will go into each account.
Answers
Answer:
$23
Step-by-step explanation:
50 + 19 is 69, and since Justin wants to divide the money into 3 parts. Just divide the total (69) by 3, to get 23. So, Justin will put $23 into the three of the accounts.
If there is a point on the grid and its (6,4) and its asking to rotate it 90 degrees clockwise what is the answer ?
Answers
4. Create a Python program (Filename: optimization.py) to perform the following optimization problem. Minimize x
3
−2cos(x)+9 s.t. 0≤x≤2 This optimization is to find the minimum value of x
3
−2cos(x)+9 when 0≤x≤2. This optimization problem can be approximately solved by simply searching in the feasible range. In the program, you can simply define a list x=[0,0.01,0.02,…,1.98,1.99,2.0] and also define an objective function as f(x)=x
3
−2cos(x)+9, and search for the minimum f(x) of different values in the list x.
Answers
Here's a Python program (Filename: optimization.py) to perform the optimization problem: Minimize x
3
−2cos(x)+9 s.t. 0≤x≤2The optimization problem is to find the minimum value of x
3
−2cos(x)+9 when 0≤x≤2. This optimization problem can be approximately solved by simply searching in the feasible range. In the program, you can simply define a list x = [0, 0.01, 0.02, …, 1.98, 1.99, 2.0]. Also, define an objective function as f(x) = x
3
−2cos(x)+9 and search for the minimum f(x) of different values in the list x.```python
import math
x = [0.01*i for i in range(201)]
min_val = 1e18
opt_x = 0
def f(x):
return x**3 - 2*math.cos(x) + 9
for xi in x:
if xi>=0 and xi<=2:
fval = f(xi)
if fval
To know more about optimization problems: https://brainly.com/question/14160739
#SPJ11
Identify a positive coterminal angle for the angle shown below. You must answer in radians.

Answers
What equation represents the line that is perpendicular to 3x+2y=-4 and passes through the point (-6,0)?
Answers
Answer:
Step-by-step explanation:
2y = -3x - 4
y = -3/2x - 2
perp.:2/3
y - 0 = 2/3(x + 6)
y = 2/3x + 4
Kyle's pancake recipe calls for a ratio of three tablespoons of sugar for every two cups of flour. How many tablespoons of sugar are needed per cup of flour? Do not include units tablespoons) in your answer
Answers
Answer:
1.5 tablespoons of sugar
Step-by-step explanation:
Given: ZADB = ZCBD ZABDZCDB m ZA= 3x + 15 mZC=8x-20 Find: x and m ZA A4 D B

Answers
Answer:
x = 7 , ∠ A = 36°
Step-by-step explanation:
since ∠ ADB ≅ ∠ CBD ( alternate angles )
and ∠ ABD ≅ ∠ CDB ( alternate angles )
then ABCD is a parallelogram
the opposite angles of a parallelogram are congruent , so
∠ C = ∠ A , that is
8x - 20 = 3x + 15 ( subtract 3x from both sides )
5x - 20 = 15 ( add 20 to both sides )
5x = 35 ( divide both sides by 5 )
x = 7
Then
∠ A = 3x + 15 = 3(7) + 15 = 21 + 15 = 36°
Answer: x = 7 and m∠A = 36
Step-by-step explanation:
Here ∠ADB ≅ ∠CBD and ∠ABD ≅ ∠CDB
This configuration is found when a quadrilateral has two parallel sides which have a diagonal as their transversal. Thus the figure is of parallelogram. In a parallelogram, opposite angles are equal. Thus m∠A = m∠C
⇒3x +15 = 8x - 20
⇒3x + 15 - 3x = 8x - 3x -20
⇒5x = 20 + 15
⇒x = 7
Now m∠A = (3X7) +15 = 36
when you solve a system of equations (i.e. two equations with two variables each), what possible form(s) could the solution take
Answers
9 didvided by 5 and 1 /7th
Answers
Answer:
7/4
Step-by-step explanation:
i am sooo sure that the answer is 1.75
The value of proper fraction are found between _ and _ in whole number
Answers
Answer:
The value of proper fractions is found in between 0 and 1.
Step-by-step explanation:
Proper fractions are fractions where the denominator is greater than the numerator.
If the numerator is greater than the denominator, then it is an improper fraction.
Common Examples of Proper fractions:
1/4, 1/2, 2/3
Common Examples of Improper fractions:
3/2, 2/1, 7/4
Someone pls explain, i’ll mark u brainliest!

Answers
Answer: (a) 2, (b) 4, (c) - 4, (d) -3. (look at the image for the solution)
Step-by-step explanation:

Consider the following data drawn independently from normally distributed populations: (You may find it useful to appropriate table: z table or t table)
xˉ1 = −17.1
s1^2 = 8.4
n1=22
xˉ2 = −16.0
s2^2 = 8.7
n2 = 24
a. Construct the 90% confidence interval for the difference between the population means. Assume the population va unknown but equal. (Round final answers to 2 decimal places.)
confidence interval is __ to __
Answers
The 90% confidence interval for the difference in the population means is -2.51 to 0.31
Calculating the 90% confidence interval for the population mean differenceFrom the question, we have the following parameters that can be used in our computation:
xˉ₁ = −17.1
s₁² = 8.4
n₁ = 22
xˉ₂ = −16.0
s₂² = 8.7
n₂ = 24
Calculate the pooled variance using
P = (df₁ * s₁² + df₂ * s₂²)/df
Where
df₁ = 22 - 1 = 21
df₂ = 24 - 1 = 23
df = 22 + 24 - 2 = 44
So, we have
P = (21 * 8.4 + 23 * 8.7)/44
P = 8.56
Also, we have the standard error to be
SE = √(P/n₁ + P/n₂)
So, we have
SE = √(8.56/22 + 8.56/24)
SE = 0.86
The z score at 90% CI is 1.645, and the CI is calculated as
CI = (x₁ - x₂) ± z * SE
So, we have
CI = (-17.1 + 16.0) ± 1.645 * 0.86
This gives
CI = -1.1 ± 1.41
Expand and evaluate
CI = (-2.51, 0.31)
Hence, the confidence interval is -2.51 to 0.31
Read more about confidence interval at
https://brainly.com/question/15712887
#SPJ1
Help me out? Thanks :)

Answers
Answer:
pretty sure its 21
Step-by-step explanation:
21 21 times 10 is 210
42
63
84
mark brainleist if right
determine the solution for the equation 2x^2+3x+1=0
Answers
Answer:
x = -1, x=-0.5
Step-by-step explanation:
Use the quadratic formula. The equation you have has a base formula of ax^2+bx+c, so if you plug the numbers into the formula and solve, it should show the answers.
What do the coordinates of an undefined slope have in common?
Answers
The coordinates of an undefined slope are points that are either the same or have no x-value. In both cases, the slope of a line between these points would be undefined because it would involve dividing by 0, which is not allowed in mathematics. This is because the slope of a line is calculated by dividing the difference in y-coordinates by the difference in x-coordinates, and if the x-coordinates are the same or do not exist, this division would result in an undefined value.
If the radioactive half-life of a substance is 20 days, and there are 5 grams of it initially. When will the amount left be 2 grams? Round to the nearest tenth of a day.
Answers
Answer: \(26.4\ \text{days}\)
Step-by-step explanation:
Given
Half life of radioactive substance is \(T_{\frac{1}{2}}=20\ \text{days}\)
Initial amount \(A_o=2\ \text{days}\)
Amount left at any time is given by
\(\Rightarrow A=A_o2^{\dfrac{-t}{T_{\frac{1}{2}}}}\\\\\Rightarrow 2=52^{\dfrac{-t}{20}}\\\\\Rightarrow 0.4=2^{\dfrac{-t}{20}}\\\\\Rightarrow 2^{\dfrac{t}{20}}=2.5\\\\\Rightarrow \dfrac{t}{20}\ln 2=\ln (2.5)\\\\\Rightarrow t=\dfrac{20\ln (2.5)}{\ln 2}\\\\\Rightarrow t=26.4\ \text{days}\)
It takes 26.4 days to reach 2 gm.
8. A shape is enlarged by a scale factor of 2. Its original area is 6cm². What is the area of the enlarged shape?..... 9. A shape has an area of 8cm². It is enlarged by a scale factor of 3. What is the area of the enlarged shape?...?.!! 10. A shape with an area of 20cm² is enlarged by a scale factor of k. What is the area of the enlarged shape? ........
Answers
Answer:
8. 24 cm²
9. 72 cm²
10. 20k²
Step-by-step explanation:
Let's come up with a rule, then we will solve all problems.
We start by answering this question.
If the area of one figure is enlarged by a scale factor of k to get to a second figure, by what factor does the area of the second figure change?
There are two figures with a scale factor of k.
For example, there is a square with side s.
Then there is a second square which is enlarged by a factor of k, k > 1.
The side of the enlarged square is ks.
area of square = (side)²
The area of the smaller square is s².
The area of the larger square is (ks)² = k²s².
scale factor from old to new = (new length) / (old length)
The scale factor is ks/s = k
The ratio of the areas is k²s²/s² = k²
From here we see that if the side is enlarged by a factor of k, then the area is enlarged by a factor of k².
The area is enlarged by the square of the scale factor. To find the new area, multiply the old area by the square of the scale factor.
Now we solve problems 8, 9, 10.
Question 8:
original area = 6 cm²
scale factor = 2 = k
factor of the area = k² = 2² = 4
enlarged area = 6 cm² × 4 = 24 cm²
Question 9:
original area = 8 cm²
scale factor = 3 = k
factor of the area = k² = 3² = 9
enlarged area = 8 cm² × 9 = 72 cm²
Question 10.
original area = 20 cm²
scale factor = k
factor of the area = k²
enlarged area = 20 cm² × k² = 20k² cm²
A bicycle tire is 28 inches in diameter. Approximately how far does the bicycle move forward each time the wheel goes around? (use 22/7 as an approximation for pi)
Answers
Answer: 88 inches
Step-by-step explanation:
A bicycle tire is 28 inches in diameter. approximately.
To find the distance traveled by the bicycle each time the wheel goes around we need to find the circumference of the tire.
The circumference of a circle: where d is the diameter of the circle.
Now, the circumference of the tire:
Hence, the distance traveled by the bicycle each time the wheel goes around =88 inches.
(5x-2)-(3x+9)
Can someone tell me the answer plz
Answers
(5x - 2) - (3x + 9)
Step one: take away the parenthesis and your equation is now 5x - 2 - 3x + 9
Step two: combine your like terms:
5x - 3x = 2x
-2 + 9 = 7
Answer: 2x + 7
ABCD is a rectangle with angleBAC =32 and find angleDBC
Answers
Answer:
Angle BAC= Angle DBC ( vertically opposite angels are equal)
Therefore, Angle DBC = 32 degree
Step-by-step explanation:
I hope it is correct.
What could be the answer?
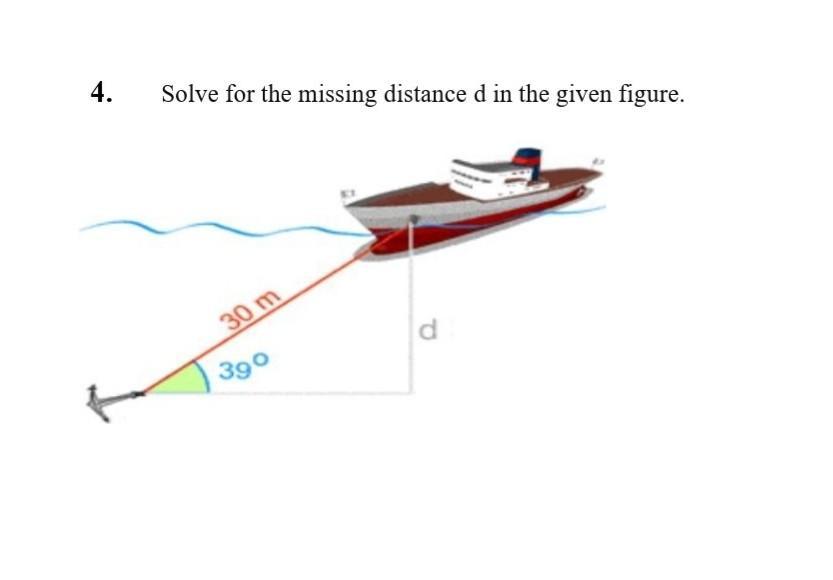
Answers
Answer:
D = 1 8.87961173
Round off to the whole number
D= 19m
Explanation of results
So to find d you will use the trigonometry formula
So you are given the
Degree which is 39°
and the hypotenuse which is 30m
Using the sin θ = Opposite Side/Hypotenuse you are going to put in the numbers where they should go in the formula so,
\( \sin(39) = \frac{d}{30} \)
then you are going to isolate d on the right by multiplying 30 on both sides.
It will look like
30 Sin 39
So, just put this in the calculator
I WILL GIVE BRAINLIEST TO RIGHT ANSWER
write an equation of the line in a slope intercept form of a line that passes through (5,7) and (4,4)
Answers
Answer:
y = 3x - 8
Step-by-step explanation:
passes through (5, 7) and (4, 4)
Find slope:
(7 - 4) / (5 - 4)
= 3/1
= 3
This is your slope.
Now plug in a set of coordinates.
y = 3x + b
7 = 3(5) + b
7 = 15 + b
b = -8
Your equation is: y = 3x - 8
Check your work by plugging in the second coordinate pair.
y = 3x - 8
4 = 3(4) - 8
4 = 12 - 8
4 = 4
Your solution is correct.