if the end behavior is decreasing to the left and increasing to the right, which statement must be true about the function?

Answer: 12cm

Step-by-step explanation:

They are similar, so we can set an equation of:

the ratio of length and width of the big triangle equal to the ratio of length and width of the small(second) triangle.

36:9 = x:3

36/9 = x/3

9x = 3(36)           by use the cross multiply

9x = 108

x = 12 cm

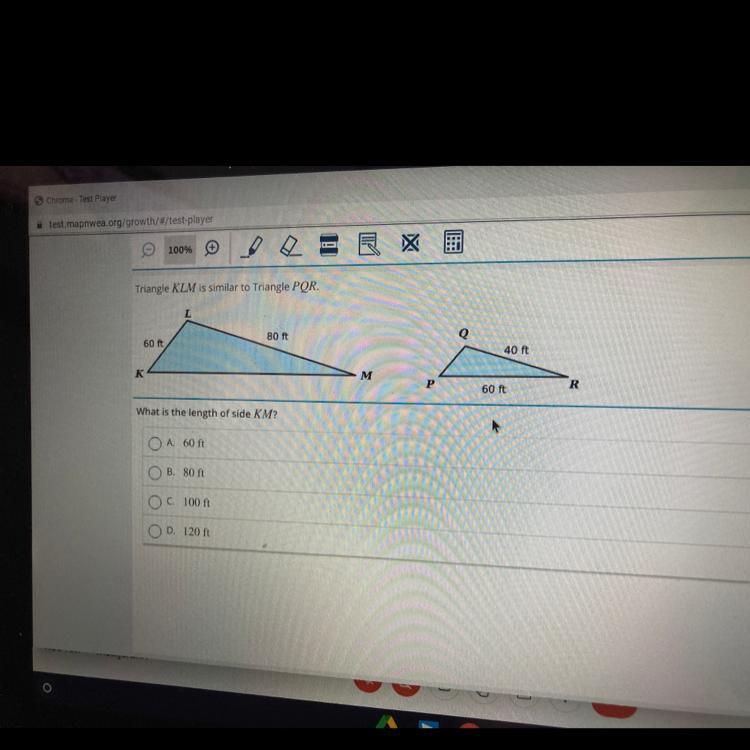
Answer:

Step-by-step explanation:

0.00048*.81=0.0003888

0.0003888*10=0.003888

0.003888*(10)=0.3888

0.3888-7=-6.6112

-6.6112*0.027=-224.8592593

-224.8592593*0.04= -9.794370372

-9.794370372*(10)=-97.94370372

-97.94370372*6= -587.6622223

The given conditional statements are false, true, false, True.

They are determined by following:

(a) False - The statement "If 10<7,10<7, then 3=43=4" is false, since 10 is not less than 7.
(b) True - The statement "If 7<10,7<10, then 3=43=4" is true, since 7 is less than 10.
(c) False - The statement "If 10<7,10<7, then 3+5=83+5=8" is false, since 10 is not less than 7.
(d) True - The statement "If 7<10,7<10, then 3+5=83+5=8" is true, since 7 is less than 10.

Conditional statements are used in mathematics and logic to express relationships between events and conditions. These statements consist of an "if-then" structure, where the "if" clause is the antecedent or condition, and the "then" clause is the consequent or outcome.

The truth value of the conditional statement depends on whether the condition is true or false. If the condition is true, then the outcome is also true, and the statement is considered true.

If the condition is false, then the outcome may be true or false, and the statement is considered false. Conditional statements are widely used in mathematical proofs, programming, and reasoning to establish logical connections between different events and conditions.

To learn more about the 'conditional statement':

https://brainly.com/question/11073037

#SPJ11

The task requires devising a recursive definition for the set S, which contains all strings from A* in which there is no b before an a.

To create a recursive definition for S, we need to consider two cases: a string that starts with an "a" and a string that starts with a "b." For the first case, we can define the set S recursively as follows:

λ ∈ S (the empty string is in S)

If w ∈ S, then aw ∈ S (concatenating an "a" at the end of a string in S results in a string that is also in S)

If w ∈ S and x ∈ A*, then \(wx\) ∈ S (concatenating any string in A* to a string in S results in a string that is also in S)

For the second case, we only need to consider the empty string because any string starting with a "b" cannot be in S. Thus, we can define S recursively as follows:

λ ∈ S

If w ∈ S and x ∈ A*, then xw ∈ S

These two cases cover all possible strings in S, as they either start with an "a" or are the empty string. By using recursive rules to concatenate characters at the beginning or end of strings in S, we can generate all valid strings in the set without generating any invalid strings that contain a "b" before an "a."

Learn more about string here:

https://brainly.com/question/27832355

#SPJ11

Answer:

-3/4

Step-by-step explanation:

We can rearrange the equation to get 3y = 4x + 27. Then we can find the slope intercept form: y = 4x/3 +9. You find the perpendicular slope by solving for the opposite and reciprocal of the current slope 4/3. So we would get -4/3, and then -3/4.

Answer: Slope of line = \(\frac{1.2}{2}\)

Graph- see picture.

Step-by-step explanation:

Graphs are graphed using y=mx+b

Slope (m) is written as \(\frac{rise}{run}\), and y coordinate is up and down, x is left & right.

The y coordinate adds 1.2 every time, so the rise is 1.2.

The x coordinate adds 2 every time, so the run is 2.

The y intercept (b) simply means where the line intercepts the y axis.

It is given that the y intercept is 0.

So, the graphing equation: y= \(\frac{1.2}{2}\)x

We don't need to put the y intercept because it is 0!

The graph is attached!

I am not a professional, simply using prior knowledge!

Answer:

10.5% (Rounds to 11% if question asked)

Step-by-step explanation:

When finding percentage increase, I usually construct a proportion, as follows

1.52. 100%

------. =. ---------

1.68. x

1.52 across from 100 because that was his actual height %

1.68 across from x because we want that new %

We start by cross multipling

1.52x = (1.68)(100)

1.52x = 168

Next we divide by 1.52 on both sides of the equal sign to get x alone

x = 110.5%

Now he's at 110.5%

We simply subtract the percent

110.5-100 = 10.5

10.5% (Rounds to 11% if question asked)

Answer:

10

Step-by-step explanation:

it is Pythagoras theorem

6*6=36

8*8=64

64+36=100

square root of 100 is 10

Answer:

A sequence is a chain of numbers all related. In this case, they are related by the rule "f(n + 1) = –10f(n)". Each number is called a term. Here is what the rule in this sequence means:

Since f(n + 1) is the "next" term and f(n) is the "current" term, to get to the next term, you take the current term and multiply by -10.

When they say f(1) = 1 it means that the first term (term number 1) is 1. When they ask "What is f(3)?", they are asking, "What is the 3rd term?"

Since term #1 is 1, then to find term #2, we multiply 1 by -10. So term #2 is -10. To find term #3, we take term #2 and multiply it by -10, so -10 x -10 = 100. So term #3 is 100

Step-by-step explanation:

The probability that at least one of the 5 people selected has been vaccinated is 0.998, or 99.8%.

To solve this problem, we can use the complement rule, which states that the probability of an event happening is equal to 1 minus the probability of the event not happening. In this case, the event we're interested in is at least one person being vaccinated.
First, we need to find the probability that none of the 5 people selected have been vaccinated. Since 62% of the population has been vaccinated, that means 38% have not been vaccinated. So the probability of any one person not being vaccinated is 0.38.
Using the multiplication rule for independent events, the probability that all 5 people have not been vaccinated is:
0.38 x 0.38 x 0.38 x 0.38 x 0.38 = 0.002
Now we can use the complement rule to find the probability that at least one person has been vaccinated:
1 - 0.002 = 0.998
So the probability that at least one of the 5 people selected has been vaccinated is 0.998, or 99.8%.

To know more about probability visit:

https://brainly.com/question/31120123

#SPJ11

To differentiate the function f(x) = qx + r/sx + t, where q, r, s, and t are constants, the derivative is given by f'(x) = q - (r/s) * (1/x^2).

To differentiate the given function, we need to apply the rules of differentiation. Let's break down the steps:

1. Differentiate qx with respect to x: Since q is a constant, the derivative of qx is simply q.

2. Differentiate r/sx with respect to x: We can rewrite r/sx as r * (s * x)^(-1). Applying the power rule of differentiation, the derivative of (s * x)^(-1) is (-1) * (s * x)^(-1 - 1) * s = -s/x^2.

3. Differentiate t with respect to x: Since t is a constant, the derivative of t with respect to x is 0.

4. Combining the derivatives obtained from the previous steps, we have f'(x) = q - (r/s) * (1/x^2).

Therefore, the derivative of the given function f(x) = qx + r/sx + t, where q, r, s, and t are constants, is f'(x) = q - (r/s) * (1/x^2).

Learn more about differentiation here:

https://brainly.com/question/24062595

#SPJ11

Answer:

Exact Form:

x=401/625

Decimal Form:

x=0.6416

Answer: x = 401/625

Step by step:

How to solve your problem

25^{2}x-1=400

Solve

1

Evaluate the exponent

2

Add

1

to both sides

3

Simplify

4

Divide both sides by the same factor

5

Simplify

Show less

Solution

Answer:

A. 3

Step-by-step explanation:

In a function, the inputs do not repeat.

The inputs are assigned to exactly one output for each.

Three is one of the options. Three is already an input in the given function.

Replacing the ? with 3 would create the non-function.

(3,5) (2, 4) (9, 0) (3,6)

Option A should be the correct answer.

Hope this helps.

Since the joint probability distribution is not equal to the product of the marginal probability distributions for all combinations of X and Y, we can conclude that the random variables X and Y are not independent. Therefore, the answer is that these random variables are not independent.

To determine whether two random variables X and Y are independent, we need to check if the joint probability distribution of X and Y is equal to the product of their marginal probability distributions.

Given the probability space (S, M, P) and the random variables X and Y defined as:

X(a) = X(b) = X(c) = 1

X(d) = X(e) = X(f) = 0

Y(a) = Y(d) = 2

Y(b) = Y(c) = Y(e) = Y(f) = 3

We can calculate the joint probability distribution as follows:

P(X = 1, Y = 2) = P({a, d}) = f(a) + f(d) =  +  =

P(X = 1, Y = 3) = P({b, c, e, f}) = f(b) + f(c) + f(e) + f(f) =  +  +  +  =

P(X = 0, Y = 2) = P({}) = f() =  =

P(X = 0, Y = 3) = P({}) = f() =  =

Next, we calculate the marginal probability distributions:

P(X = 1) = P({a, b, c, d, e, f}) = f(a) + f(b) + f(c) + f(d) + f(e) + f(f) =  +  +  +  +  +  =

P(X = 0) = P({}) = f() =  =

P(Y = 2) = P({a, d}) = f(a) + f(d) =  +  =

P(Y = 3) = P({b, c, e, f}) = f(b) + f(c) + f(e) + f(f) =  +  +  +  =

Now, let's check if the joint probability distribution is equal to the product of the marginal probability distributions:

P(X = 1, Y = 2) = P(X = 1) * P(Y = 2)

P(X = 1, Y = 3) = P(X = 1) * P(Y = 3)

P(X = 0, Y = 2) = P(X = 0) * P(Y = 2)

P(X = 0, Y = 3) = P(X = 0) * P(Y = 3)

Since the joint probability distribution is not equal to the product of the marginal probability distributions for all combinations of X and Y, we can conclude that the random variables X and Y are not independent.

Therefore, the answer is that these random variables are not independent.

Visit here to learn more about joint probability distribution brainly.com/question/32099581

#SPJ11

Step-by-step explanation:

Hope it will help you a lot.

If Abby deposited $3000 and has $3600 at the end of 8 years, then the interest-rate is 2.5%.

The "Simple-Interest" is the interest which is calculated based only on principle amount of a loan or investment, without taking into account any additional interest earned on previous periods.

We can use the simple interest formula to find the annual interest rate:

⇒ Simple Interest = Principle × Rate × Time,

Where: Principle is = initial deposit of $3000,

Rate = annual interest rate (what we need to find)

Time = number of years the money was invested = 8,

The Simple Interest earned over 8 years : $3600 - $3000 = $600,

Substituting the values,

We get,

⇒ $600 = $3000 × Rate × 8,

⇒ Rate = 600/(3000 × 8),

⇒ Rate = 0.025, or 2.5%.

Therefore, the annual interest rate on the account is 2.5%.

Learn more about Simple Interest here

https://brainly.com/question/30964674

#SPJ1

The required percentage of regular grade gasoline are;

a) 34%

b) 95.5%

c)4.5%

(a) To determine the percentage of regular grade gasoline sold between $3.25 and $3.65 per gallon, we need to find the proportion of the data that falls within this range. Assuming a bell-shaped distribution, we can use the standard deviation and mean to find the z-scores for these two prices, and then look up the cumulative probability in a standard normal table.

$3.25$ is $1$ standard deviation below the mean and $3.65$ is $0.5$ standard deviation above the mean.

Using a standard normal table, we find that approximately 68% of the data falls within one standard deviation of the mean, and approximately 34% falls between $-0.5$ and $0.5$ standard deviations.

Therefore, approximately 34% of regular grade gasoline is sold between $3.25 and 3.65 per gallon.

(b) To find the percentage of regular grade gasoline sold between $3.25 and $3.85 per gallon, we need to find the cumulative probability for the range $3.25$ to $3.85$.

$3.85$ is $1.5$ standard deviations above the mean.

Using a standard normal table, we find that approximately 95.5% of the data falls within $1.5$ standard deviations of the mean.

Therefore, approximately 95.5% of regular grade gasoline is sold between $3.25 and $3.85 per gallon.

(c) To find the percentage of regular grade gasoline sold for more than $3.85 per gallon, we need to find the cumulative probability for values greater than $3.85$.

Using a standard normal table, we find that approximately 100% - 95.5% = 4.5% of the data falls above $1.5$ standard deviations from the mean.

Therefore, approximately 4.5% of regular grade gasoline is sold for more than $3.85 per gallon.

To know more about Percentage visit:

brainly.com/question/28269290

#SPJ4

Answer: 4.4 + (4 x 1/4 + 8.6) = 14

Step-by-step explanation: Because starting inside the parenthesis, 4 times 1/4 = 1. Then 8.6 plus 1 = 9.6. Finally, 9.6 plus 4.4 which equals 14. :)

Answer:140mph

Step-by-step explanation:

The criteria that we could use to prove the congruency that ΔABC ≅ ΔDEC is;

Vertical Angles are Congruent. We could then use AAS to prove that ΔABC ≅ ΔDEC

There are different triangle congruency postulates namely:

SSS: Side Side Side Congruency Postulate

SAS: Side Angle Side Congruency Postulate

ASA: Angle Side Angle Congruency Postulate

AAS: Angle Angle Side Congruency Postulate

HL: Hypotenuse Leg Congruency Postulate

We want to prove that ΔABC ≅ ΔDEC

Now, from the given image, we see that we are given 2 congruent sides.

However, angle ECD is congruent to angle DCA because they are vertically opposite angles and vertical angles are congruent.

Thus, the triangles are congruent by AAS Congruency postulate.

Read more about Triangle Congruence Postulate at; https://brainly.com/question/29268713

#SPJ1

Answer: I think B

Step-by-step explanation:

For a loan, simple interest makes the customer pay interest only for the amount of the loan.

Compound interest makes the customer pay interest for the loan balance at the end of each payment period. In other words, the customer pays interest over interest based on the remaining balance.

Of course, the best option for the bank is that the customer pays more often so the interest adds up more times for the loan duration.

The daily compound interest is the best choice for the bank because the loan recalculates every day, that is, 360 (or 365) times a year as compared to the monthly, quarterly, or yearly compound interest.

Answer: E. Compound interest daily

Answer:

2x=50   x=25

Step-by-step explanation:

Answer:

x = 25

Step-by-step explanation:

6x - 20 = 4x + 30 (Since, lines are parallel and They are Corresponding angles)

=> 6x - 4x = 30 + 20

=> 2x = 50

=> x = 25

Answer:

2 and -1/2 since -1/2 is negative the answer is 2

Step-by-step explanation:

I plugged the values into the quadratic formula

well, from 1990 to 1998 is 8 years, and we know the amount went from $4800 to $6300, let's check for the rate of growth.

\(\qquad \textit{Amount for Exponential Growth} \\\\ A=P(1 + r)^t\qquad \begin{cases} A=\textit{accumulated amount}\dotfill & \$6300\\ P=\textit{initial amount}\dotfill &\$4800\\ r=rate\to r\%\to \frac{r}{100}\\ t=\textit{years}\dotfill &8\\ \end{cases} \\\\\\ 6300=4800(1 + \frac{r}{100})^{8} \implies \cfrac{6300}{4800}=(1 + \frac{r}{100})^8\implies \cfrac{21}{16}=(1 + \frac{r}{100})^8\)

\(\sqrt[8]{\cfrac{21}{16}}=1 + \cfrac{r}{100}\implies \sqrt[8]{\cfrac{21}{16}}=\cfrac{100+r}{100} \\\\\\ 100\sqrt[8]{\cfrac{21}{16}}=100+r\implies 100\sqrt[8]{\cfrac{21}{16}}-100=r\implies \stackrel{\%}{3.46}\approx r\)

now, with an initial amount of $4800, up to 2007, namely 17 years later, how much will that be with a 3.46% rate?

\(\qquad \textit{Amount for Exponential Growth} \\\\ A=P(1 + r)^t\qquad \begin{cases} A=\textit{accumulated amount}\\ P=\textit{initial amount}\dotfill &4800\\ r=rate\to 3.46\%\to \frac{3.46}{100}\dotfill &0.0346\\ t=years\dotfill &17\\ \end{cases} \\\\\\ A=4800(1 + 0.0346)^{17} \implies A=4800(1.0346)^{17}\implies A \approx 8558.02\)