if the average collection period is 100.0 days, what is the accounts receivable turnover? (round your answer to 2 decimal places.) 7.30 times 3.65 times 4.65 times 14.60 times
Answers
The accounts receivable turnover is approximately 3.65 times.
We can use the formula:
Accounts Receivable Turnover = Net Credit Sales / Average Accounts Receivable
However, we need additional information to calculate this. Specifically, we need to know the net credit sales and the average accounts receivable.
The average collection period is a measure of how long it takes for accounts receivable to be collected. It is calculated as:
Average Collection Period = (Accounts Receivable / Net Credit Sales) x 365
We can rearrange this formula to solve for the accounts receivable:
Accounts Receivable = (Average Collection Period / 365) x Net Credit Sales
We are given that the average collection period is 100.0 days. Assuming a 365-day year, we have:
Accounts Receivable = (100.0 / 365) x Net Credit Sales
Accounts Receivable = 0.27397 x Net Credit Sales
Now we can use the accounts receivable turnover formula:
Accounts Receivable Turnover = Net Credit Sales / Average Accounts Receivable
Accounts Receivable Turnover = Net Credit Sales / (0.27397 x Net Credit Sales)
Accounts Receivable Turnover = 1 / 0.27397
Accounts Receivable Turnover ≈ 3.65
Therefore, the accounts receivable turnover is approximately 3.65 times.
To know more about Accounts Receivable Turnover refer here
https://brainly.com/question/16447941#
#SPJ11
Related Questions
Rachel ran 3 miles when she was training for a race. How many feet did she run?
Answers
Answer:
15,840 i did this in test and got 100%
Step-by-step explanation:
The total feet ran by Rachel is given by the equation A = 15,840 feet
What is an Equation?Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given data ,
Let the equation be represented as A
Now , the value of A is
Let the total miles ran by Rachel be A = 3 miles
Now , the value of 1 mile = 5,280 feet
Substituting the values in the equation , we get
The distance of 3 miles in feet = 3 x value of 1 mile
On simplifying the equation , we get
The distance of 3 miles in feet = 3 x 5,280
The distance of 3 miles in feet = 15,840 feet
Therefore , the distance ran by Rachel A = 15,840 feet
Hence , the equation is A = 15,840 feet
To learn more about equations click :
https://brainly.com/question/19297665
#SPJ6
I’m giving brainlest pls help meeee

Answers
Answer:
gggggjwjwkekdbfjfnnf
Answer:
B is the correct answer
Step-by-step explanation:
Hope it helped have a great day
You are shopping for single-use cameras to hand out at a party. The daylight cameras cost $2.75 and the flash cameras cost$4.25. You must buy exactly 20 cameras and you want to spend between $65 and$75, inclusive. Write and solve a compound inequality for this situation. Then list all the solutions that involve whole numbers of cameras.
Answers
The compound inequality for the given situation is $2.75x + $4.25y ≥ $65 and $2.75x + $4.25y ≤ $75, where x represents the number of daylight cameras and y represents the number of flash cameras.
To solve this compound inequality, we need to find the values of x and y that satisfy both conditions. The inequality $2.75x + $4.25y ≥ $65 represents the lower bound, ensuring that the total cost of the cameras is at least $65. The inequality $2.75x + $4.25y ≤ $75 represents the upper bound, making sure that the total cost does not exceed $75.
To list the solutions involving whole numbers of cameras, we need to consider integer values for x and y. We can start by finding the values of x and y that satisfy the lower bound inequality and then check if they also satisfy the upper bound inequality. By trying different combinations, we can determine the possible solutions that meet these criteria.
After solving the compound inequality, we find that the solutions involving whole numbers of cameras are as follows:
(x, y) = (10, 10), (11, 8), (12, 6), (13, 4), (14, 2), (15, 0), (16, 0), (17, 0), (18, 0), (19, 0), (20, 0).
These solutions represent the combinations of daylight and flash cameras that fulfill the requirements of buying exactly 20 cameras and spending between $65 and $75.
Learn more about compound inequality
brainly.com/question/17957246
#SPJ11
you bought a new car for $17,896. as you drive off the lot , the car depreciates by 6.3%. what will the value of the car be in 9 years ?
Answers
Answer: at the end of year 9 the car value would be $9963,5
Step by step:
Every year you lose 6.30% of the last value, so from the last year's value you take out another 6.3%.
every year the formula is the same, so based on first year it would be:
$17896 * (100%-6.3%) = $17896 * 93.5% = $16768.6
year 1 17896,0 6,30%
year 2 16768,6 6,30%
year 3 15712,1 6,30%
year 4 14722,3 6,30%
year 5 13794,8 6,30%
year 6 12925,7 6,30%
year 7 12111,4 6,30%
year 8 11348,4 6,30%
year 9 10633,4 6,30%
end of year 9 = 9963,5
I NEED A ANSWER ASAP!!
A dog park is 100 yards long and the town wants to install water bowls for their beloved pups. If the town wants a water bowl at each end and every 20 yards i
between, how many water bowls need to be installed?
Answers
Answer:
5
Step-by-step explanation:
5*20=100
A statistical test used to help answer the question of whether an observed difference is real or just due to chance error.a. trueb. false
Answers
a. A statistical test used to help answer the question of whether an observed difference is real or just due to chance error- true
The statistical test referred to in the question is known as a hypothesis test. It is used to determine the probability that the observed difference between two groups or variables is not due to chance but rather represents a true difference. The test involves setting up a null hypothesis, which assumes that there is no difference between the groups or variables, and an alternative hypothesis, which assumes that there is a real difference.
The test calculates a p-value, which represents the probability of obtaining the observed difference by chance if the null hypothesis is true.
If the p-value is below a predetermined level of significance (usually 0.05), then the null hypothesis is rejected and the alternative hypothesis is accepted.
This means that the observed difference is considered real and not just due to chance error.
Hence, If the p-value is below a certain level of significance, the null hypothesis is rejected and the alternative hypothesis is accepted, indicating that the observed difference is real.
learn more about hypothesis click here:
https://brainly.com/question/606806
#SPJ11
the mayor of a city randomly chooses 4 of the 20 wards in her city and surveys all the voters in those selected wards.
Answers
The sample space is 4845.Therefore, option C is correct.
Given: The mayor of a city randomly chooses 4 of the 20 wards in her city and surveys all the voters in those selected wards.
Solution: We have a sample size of 4 wards out of a total of 20 wards. The mayor has chosen all the voters in those 4 wards. So, the sampling method used here is stratified sampling as the mayor chose the voters of specific 4 wards.
Sample space = Total number of ways to select 4 wards out of 20 wards= C(20,4) = 20!/(4!(20 - 4)!) = 4845
Hence, the sample space is 4845.Therefore, option C is correct.
Learn more about sample space visit:
brainly.com/question/30206035
#SPJ11
Find the length of b to the nearest tenth.
(BRAINLIEST :D)
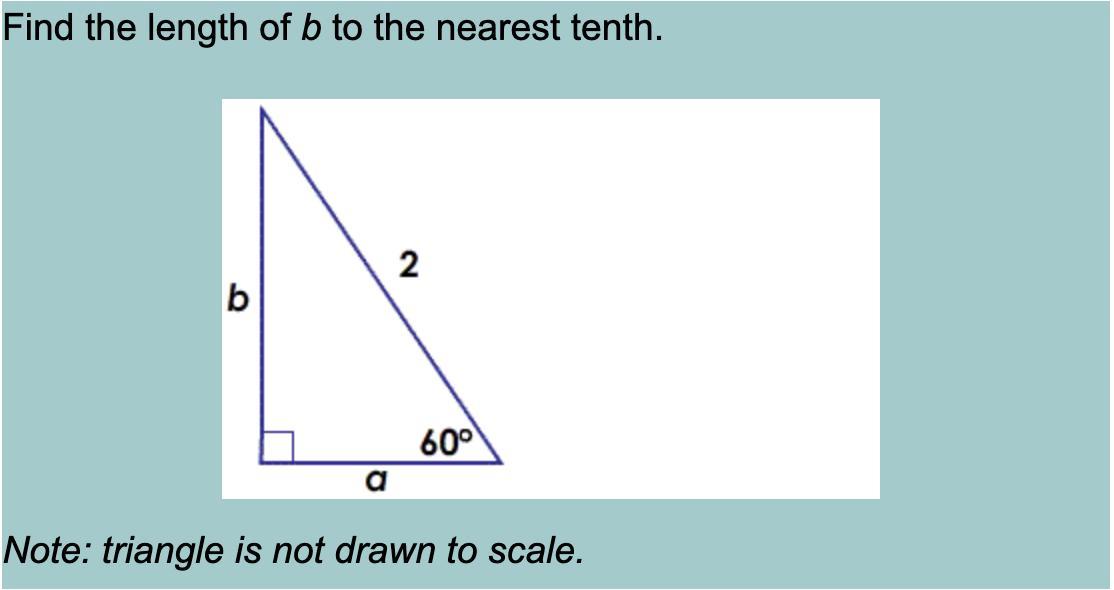
Answers
Answer:
1.7
Step-by-step explanation:
You can use the 30/60/90 triangle rule, but it was quicker for me to do. SIN(60)=b/2. If you want a more in depth explanation just reply to this but I have to go right now so I will do it later.
The signal x[n] = u[n] - u[n − 3] is applied to an LTI system whose impulse response is: h[n] = = (1/2)^n u[n] - (a) Find the output y[n]. - (b) Show that the system is stable or unstable, as the case may be.
Answers
The impulse response is absolutely summable and hence, the system is stable. Therefore, the system is stable.
The given signal x[n] is;
\($$x[n] = u[n] - u[n-3]$$\)
The impulse response of the system is given as:
\($$h[n] = \left(\frac{1}{2}\right)^nu[n]$$\)
Now, the output of a linear time-invariant (LTI) system is given by;
\($$y[n] = x[n] * h[n]$$\)
Where, * represents the convolution operation. Hence, we need to find the convolution of the input signal x[n] with the impulse response of the system h[n].
(a) Convolution of the given input signal x[n] with the given impulse response h[n] is given as:
\($$\begin{aligned} y[n] &= x[n] * h[n] \\ &= \sum_{k=-\infty}^{\infty} x[k]h[n-k] \\ &= \sum_{k=-\infty}^{\infty} (u[k] - u[k-3]) \left(\frac{1}{2}\right)^{n-k} u[n-k] \end{aligned}$$\)
Now, let's break this equation into two parts, one for \($0 \leq n < 3$\) and other for \($n \geq 3$\).
For \($0 \leq n < 3$\), the above equation can be simplified as:
\($$\begin{aligned} y[n] &= \sum_{k=0}^{n} \left(\frac{1}{2}\right)^{n-k} \\ &= \frac{1}{2^n} \sum_{k=0}^{n} \left(\frac{1}{2}\right)^k \\ &= \frac{1}{2^n} \cdot \frac{1 - \left(\frac{1}{2}\right)^{n+1}}{1 - \frac{1}{2}} \\ &= 1 - \frac{1}{2^{n+1}} \end{aligned}$$\)
For\($n \geq 3$\), the above equation can be simplified as:
\($$\begin{aligned} y[n] &= \sum_{k=n-2}^{n} \left(\frac{1}{2}\right)^{n-k} \\ &= \frac{1}{2^3} + \frac{1}{2^2} + \frac{1}{2^1} \\ &= \frac{7}{8} \end{aligned}$$\)
Therefore, the output of the given system is:
\($$y[n] = \begin{cases} 1 - \frac{1}{2^{n+1}} & \text{for } 0 \leq n < 3 \\ \frac{7}{8} & \text{for } n \geq 3 \end{cases}$$\)
(b) The system is said to be stable if the impulse response is absolutely summable, that is,
\($$\sum_{n=-\infty}^{\infty} |h[n]| < \infty$$\)
Now, let's check whether the given system is stable or not:
\($$\sum_{n=-\infty}^{\infty} |h[n]| = \sum_{n=0}^{\infty} \left(\frac{1}{2}\right)^n = \frac{1}{1 - \frac{1}{2}} = 2 < \infty$$\)
Since the above sum is a finite quantity, the impulse response is absolutely summable and hence, the system is stable. Therefore, the system is stable.
to know more about linear time-invariant visit:
https://brainly.com/question/31041284
#SPJ11
El triángulo ABC es equilátero y L, M y N son los puntos medios de BC, AB y CA respectivamente. Si MN = 3, ¿cuál es el valor de ML?

Answers
The value of ML = 3, using the mid-point theorem of triangles.
According to the midpoint theorem, "the line segment of a triangle crossing the midpoints of two sides of the triangle is said to be parallel to its third side and also half the length of the third side."
In the question, we are given that triangle ABC is an equilateral triangle, and L, M, and N are the midpoints of BC, AB, and CA respectively.
Thus, by the midpoint theorem, we can say that:
MN || BC, and MN = (1/2)BC,ML || AC, and ML = (1/2)AC, andNL || AB, and NL = (1/2)AB.Assuming AB = BC = AC = x units, we get:
MN = (1/2)BC = x/2,ML = (1/2)AC = x/2, andNL = (1/2)AB = x/2.
Thus, the triangle LMN is an equilateral triangle.
Thus, MN = ML = NL.
Given MN = 3, we can write the value of ML = 3.
Thus, the value of ML = 3, using the mid-point theorem of triangles.
Learn more about the mid-point theorem of triangle at
https://brainly.com/question/9635025
#SPJ1
The given question is in Spanish. The question in English is:
"Triangle ABC is equilateral and L, M, and N are the midpoints of BC, AB, and CA respectively. If MN = 3, what is the value of ML?"
4 = -(x + 3) implemented as a real life problem
Answers
The control panel in a nuclear power plant contains 50 diodes. Based on testing individual diodes, the probability that any particular diode will fail prior to its scheduled replacement is known to be 0.0001. Based on the construction of the control panels, the failure of an individual diode is independent of the failure of any other diode on the control panel. During a 30 day period, the number D of failed diodes out of the 50 diodes on the control panel is recorded. The distribution of D is
Answers
The distribution of D, the number of failed diodes, follows a binomial distribution with parameters n = 50 and p = 0.0001.
The distribution of D, the number of failed diodes out of the 50 diodes on the control panel, can be modeled using the binomial distribution.
In this case, each diode can either fail (with probability 0.0001) or not fail (with probability 1 - 0.0001 = 0.9999).
The binomial distribution is defined by two parameters: the number of trials (n) and the probability of success on each trial (p).
The number of trials is 50 (corresponding to the 50 diodes) and the probability of success (p) is 0.0001 (the probability that any particular diode will fail).
To learn more on probability click:
https://brainly.com/question/11234923
#SPJ4
i do not understand how to do this can someone pls help me with this question i’m trying to get a good grade

Answers
Answer:
63 ft^2
Step-by-step explanation:
3x3 + 6x9 = 63 ft^2
Solve: 3x²+9x+6 = 0
Thank you.
Answers
Given quadrant equation:
3x² + 9x + 6 = 0
Here we see that,
→ Product of coefficient of x² and constant term = 3 × 6 = 18
→ Sum of coefficient of x² ans constant term = 3 + 6 = 9
So the given equation can be written as,
⇛3x² + 6x + 3x + 6 = 0
On taking the common terms, we get
⇛3x(x + 2) + 3(x + 2) = 0
On grouping the common terms, we get
⇛(3x + 3)(x + 2) = 0
Here either (3x + 3) = 0 or (x + 2) = 0. So,
⇛3x + 3 = 0 or x + 2 = 0
⇛3x = -3 or x = -2
⇛x = -3/3 or x = -2
⇛x = -1 or x = -2
also read similar questions:- These are the two roots of the equation.
Julian used these steps to solve the equation 9x=?6+3(3x+2) 9 x = - 6 + 3 ( 3 x + 2 ) . Which choice describes the meaning of his result, 0=0 ?
https://brainly.com/question/11808722?referrer
many academic institutions offer a sabbatical policy. every seven years a professor is given a year free of teaching and other administrative responsibilities at full pay. for a professor earning $70,000 per year who works for a total of 42 years, what is the present value of the amount she will earn while on sabbatical if t
Answers
Present value of the amount she will earn while on sabbatical if the interest rate is 6% is $126,964.34
The value of money reduces as time passes, this is due to the interest factor. $1 is worth more today than tomorrow this is because of the time value of money. The present value of cash flows is discounted value of future cash flows. Discount factors at a given rate of interest are used to find out the present value of cash flows.
Here, the professor will receive $70,000 every 7 years for 42 years.
Hence he will receive $70,000 sabbatical in the 7th, 14th,21st,28th,35th, and 42nd years.
We will find the present value of such receipts and add them.
R=0.06
F=$70,000
\(Present~Value = \displaystyle\frac{FV}{(1+r)^7}+\frac{FV}{(1+r)^{14}}+\frac{FV}{(1+r)^{21}}+\frac{FV}{(1+r)^{28}}+\frac{FV}{(1+r)^{35}}+\frac{FV}{(1+r)^{42}}\)
\(Present~Value = \displaystyle\frac{70,000}{(1.06)^7}+\frac{70,000}{(1.06)^{14}}+\frac{70,000}{(1.06)^{21}}+\frac{70,000}{(1.06)^{28}}+\frac{70,000}{(1.06)^{35}}+\frac{70,000}{(1.06)^{42}}\)
=$126,964.34
Learn more about present value:
https://brainly.com/question/17322936
#SPJ4
The diameter of a car wheel is 60 cm, if the car travels at an average speed of 13.2m/s, find the number of revolutions made by the car per hour , hiving the awnser correct to nearest whole number. (take pie to be 3.142 )
Answers
The wheel has diameter 60 cm = 0.60 m, and thus circumference π(0.60 m) ≈ 5.923 m.
In one complete revolution, a point on the edge of the wheel covers this distance, so that the wheel has an angular speed of
(13.2 m/s) * (1/5.923 rev/m) ≈ 2.229 rev/s
There are 60 seconds to each minute, and 60 minutes to each hour, so converting to rev/h gives
(2.229 rev/s) * (60 s/min) * (60 min/h) ≈ 8024 rev/h
There are 6 friends baking bread. They equally share 3 sticks of butter. Write an equation to find the fraction of a stick of butter that each friend uses. 3 sticks of butter Choose the correct answer below. A. 3÷6= 6 3 B. 3÷6= 3 6 C. 6÷3= 3 6 D. 6÷3= 6 3
Answers
Answer:
B.
Step-by-step explanation:
the three sticks of butter were divided among six people
Titus and Theresa have collected money and are buying food for a dog shelter. Titus buys 2 bags and 5 cans of dog food, spending $17.50. Theresa buys 6 bags and 2 cans of dog food for $40.80. Let x represent the price of a bag of dog food and y represent the price of a can of dog food. Write a system of equations and use the elimination method to find a reasonable price for a can of dog food.
A)$0.90
B)$1.70
C)$6.30
D)$6.50
Answers
Ava had $28.50 to spend at the farmer's market. After buying 3 pumpkins Ava, has $12 left.
Q.1 Which equation could you use to find the price of one pumpkin (x)?
Q.2 How much did Ava pay for each pumpkin?
Answers
Question 1: 28.50 - 3x = 12
Question 2: $5.50
Answer:
Step-by-step explanation:
Question 1: 28.50 - 3x = 12
Question 2: $5.50
This is the graph of f(x). Wha is the value of f(2)

Answers
Answer: 2
Step-by-step explanation:
They are saying that x equals 2, and the question is what the function is defined at when x = 2
Going to x = 2, the y value is just 2
The answer is 4.
f(2)=4
What is the range for this set of data? 7, 15, 12Mrs. Juarez graded ten English papers and recorded the scores. 92, 95, 100, 62, 88, 90, 100, 96, 89, 98 Which statements are true? Check all that apply.
Answers
Answer:
Following are the solution to the given question:
Step-by-step explanation:
Please find the complete question in the attached file.
Arrange the value into the ascending order:
\(62, 88, 89, 90, 92, 95, 96, 98, 100, 100\)
Calculating the Range:
\(= Greatest - Lowest\\\\= 100 - 62\\\\ = 38\)
Outlier = This might be the value "far" from other data values= 62
The range of scores would be, sans outlier,
\(88, 89, 90, 92, 95, 96, 98, 100, 100\)
Calculating the range without outlier \(= 100 - 88 = 12\)
Inter Quartile Range \(= Q_3 - Q_1\)
\(IQR = 98 - 89 = 11\)
Calculating the IQR without outlier \(= 99 - 89.5 = 9.5\)
Therefore,
Option a is "True".
Option b is "True".
Option c is "True".
Option d is "False".
Option e is "False".
Option f is "True".

PLEASE HELP ANSWER FAST AND ADD AN EXPLANATION!!

Answers
The total mass of the paperclips in the box is 6. 144 × 10^1 mg. Option C
1 mass of a paperclip = 8.0 × 10−4 mg
But there are 7.68 × 104 paperclips = x mg
cross multiply
x = 7.68 × 104 × 8.0 × 10−4 mg
Multiply through
x = 61. 44 × 10^ 4 -4
x = 61. 44 × 1
x = 6. 144 × 10^1 mg
Thus, the total mass of the paperclips in the box is 6. 144 × 10^1 mg. Option C
Learn more about scientific notation here:
brainly.com/question/27862246
a study was designed to investigate the effects of two variables (1) a student's level of mathematical anxiety and (2) teaching method , on a student's achievement in a mathematics course. students who had a low level of mathematical anxiety were taught using the traditional expository method. these students obtained a mean score of 370 with a standard deviation of 50 on a standardized test. assuming a mound-shaped and symmetric distribution, in what range would approximately 95% of the students score?
Answers
On a test with a range of 110–410, these students received a mean score of 370 and a standard deviation of 50. What range would roughly 95% of the students' scores fall into, presuming a mound-shaped and symmetric distribution.
A variable is what?Any traits, figures, or amounts that may be gauged or counted are considered variables. Another name for a variable is a data item. Variables include things like age, sex, business income and expenses, birthplace, capital expenditures, class grades, eye color, and vehicle type.
Which examples use variables?A variable is a quality that may be measured and take on several values. A few examples of variables are height, age, income, province of birth, school grades, and kind of dwelling. Categorical and numeric variables are the two basic types of variables that can be categorized.
h(x)=12x+3 evaluate h(6)
Answers
Answer:
75
Step-by-step explanation:
Substitute 6 in for x:
12(6)+3 –––Multiply 12 by 6
72 + 3 –––Add 72 and 3
75 –––Your answer
Find the image of -2 under the function f(x) =2x-1
Answers
Answer:
- 5
Step-by-step explanation:
Substitute x = - 2 into f(x)
f(- 2) = 2(- 2) - 1 = - 4 - 1 = - 5
The standard formulas for the derivatives of sine and cosine are true no matter if the angle is in radians or degrees. true or false
Answers
The correct option is False. The standard formulas for the derivatives of sine and cosine are true when the angle is in radians. These formulas are derived based on the properties of the trigonometric functions in the context of radians. The derivatives of sine and cosine with respect to an angle measured in radians are as follows:
\(\[\frac{d}{dx}(\sin(x)) = \cos(x)\]\)
\(\[\frac{d}{dx}(\cos(x)) = -\sin(x)\]\)
If the angle is measured in degrees, these formulas would not hold true. To differentiate trigonometric functions when the angle is measured in degrees, conversion factors and additional adjustments would be necessary.
To know more about functions visit-
brainly.com/question/2273042
#SPJ11
solve the linear equation 4x-(2x-1)=x+5+x-6
Answers
The linear equation doesn't have a solution.
How to compute the value?The linear equation given is illustrated as: 4x-(2x-1) = x+5+x-6
This will be solved thus:
4x - 2x + 1 = x+5+x-6
4x - 2x + 1 = 2x - 1.
2x + 1 = 2x - 1
Collect like terms
2x - 2x = -1 - 1
0 = -2
This illustrates that the equation doesn't have a solution.
Learn more about equations on:
brainly.com/question/28280501
#SPJ1
Determine whether each statement is True or False. Select the correct cell in each row. Statement True False T h e s u m o f − 9 a n d 18 2 i s e q u a l t o 0. The sum of −9 and 2 18 is equal to 0. T h e s u m o f − 14 2 a n d 7 i s g r e a t e r t h a n 0. The sum of − 2 14 and 7 is greater than 0. T h e s u m o f 6 , − 4 , a n d − 2 i s e q u a l t o 0. The sum of 6, −4, and −2 is equal to 0. T h e s u m o f 7 , − 9 , a n d 2 i s l e s s t h a n 0. The sum of 7, −9, and 2 is less than 0.
Answers
Each of the statements should be marked correctly as follows;
The sum of −9 and 18/2 is equal to 0: True.
The sum of −14/2 and 7 is greater than 0: False.
The sum of 6, −4, and −2 is equal to 0: True.
The sum of 7, −9, and 2 is less than 0: False.
What is an inequality?In Mathematics and Geometry, an inequality simply refers to a mathematical relation that is typically used for comparing two (2) or more numerical data and variables in an algebraic equation based on any of the inequality symbols;
Greater than (>).Less than (<).Greater than or equal to (≥).Less than or equal to (≤).Next, we would evaluate each of the statements as follows;
-9 + 18/2 = -9 + 9 = 0
Therefore, the sum of −9 and 18/2 is truly equal to 0.
-14/2 + 7 = -7 + 7 = 0.
Therefore, the sum of −14/2 and 7 is not greater than 0.
6 - 4 - 2 = 0
Therefore, the sum of 6, −4, and −2 is truly equal to 0.
7 - 9 + 2 = 0
Therefore, the sum of 7, −9, and 2 is not less than 0.
Read more on inequality here: brainly.com/question/27976143
#SPJ1


200 = 1000 - n/4. What is the value of n? Show working out, please.
Answers
Answer:
n = 3200
Step-by-step explanation:
200 = 1000 - \(\frac{n}{4}\) ( subtract 1000 from both sides )
- 800 = - \(\frac{n}{4}\) ( multiply both sides by 4 to clear the fraction )
- 3200 = - n ( multiply both sides by - 1 )
n = 3200
Identify the highlighted part of circle O shown below
Central angle
Secant
Inscribed angle
Chord

Answers
Answer:
Chord
Step-by-step explanation:
Notice that the highlighted part is the line segment that joins the points J and E on the circle, which is known as a chord.