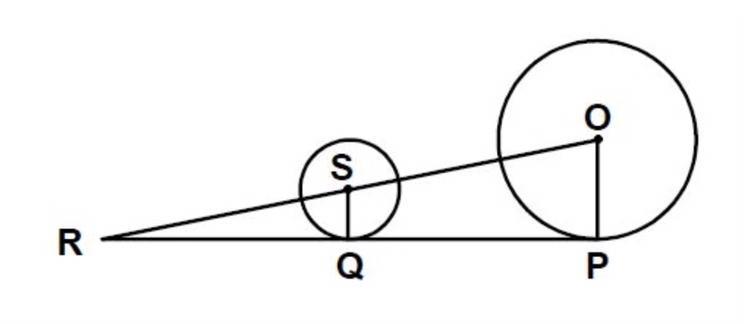
Answers
Given that
\(\begin{gathered} OP=14 \\ SQ=7 \\ QR=24 \\ PR=\text{?} \end{gathered}\)Using the method of the ratio of similar figures,
Which says
\(\frac{OP}{SQ}=\frac{PR}{QR}\)Therefore,
\(\frac{14}{7}=\frac{PR}{24}\)Solving for PR
First of all, we will cross-multiply
\(\begin{gathered} 7\times PR=14\times24 \\ 7PR=14\times24 \end{gathered}\)Then, we will divide both sides by 7
\(\begin{gathered} \frac{7PR}{7}=\frac{14\times24}{7} \\ PR=2\times24=48 \\ \therefore PR=48 \end{gathered}\)Hence,
\(PR=48\text{units}\)Related Questions
Use a ruler and compasses to answer this question.
The map of an island is shown below.
F
•Y
F
A treasure chest has been buried
on the island so that it is the same
distance from X as it is from Y.
Construct a line on the map to
show all the possible places
where the chest could be. Worth 80 points :)
Answers
The line segment joining the points X and Y on the map, which shows all the possible places where treasure chest can be found is drawn.
Explain about the line segment?In geometry, a line is just a straight, one-dimensional shape that never ends in either direction. It doesn't have a beginning or an end.
A ray is what we term a line that has a defined beginning but no defined end. A line segment is a crucial phrase related to the line.A line segment is just a section or chunk of a line that enables the construction of polygons, calculation of slopes, and slope determination. The two extremities of it indicate its finite length.The grid created by an x-axis and a y-axis is known as a coordinate plane, sometimes known as a Cartesian plane. It can be visualised as a map of the area occupied with line segments or as two perpendicular decimals.The location X and Y are given on the map.
Using the compass: draw the line joining the points X and Y.
Thus, the line segment joining the points X and Y on the map, which shows all the possible places where treasure chest can be found is drawn.
Know more about the line segment
https://brainly.com/question/19054042
#SPJ1
4- Employees at a certain company currently have to pay 7% of their health care costs,
while the company pays the rest. Next year, however, employees will have to pay 14%
of their health care costs. Express this change as:
absolute change (in percentage points) =
relative change =
Answers
Answer:
The absolute change would be 3 percentage points.
The relative change would be 100%
Step-by-step explanation:
Marilyn saves 4% of her income. If she saves $80 per month, find her
monthly income.
Answers
Using the given information, Marilyn's monthly income is $2000
Calculating monthly incomeFrom the question, we are to determine Marilyn's monthly income.
Let Marilyn's monthly income be x
From the given information,
"Marilyn saves 4% of her income"
That is,
Marilyn saves 4% of x
Also, from the given information,
She saves $80 per month
Then, we can write that
4% of x = $80
Now, we will determine the value of x
4% of x = $80
4% × x = $80
0.04 × x = $80
x = $80/0.04
x = $2000
Hence, her income is $2000
Learn more on Calculating monthly income here: https://brainly.com/question/14620435
#SPJ1
f(x)=5x-25 What is the domain of the function?
Answers
Answer:
Domain: All Real Numbers
Step-by-step explanation:
Since this function is a linear function, it will use any x-value in order to continue with being a linear function. Therefore, if the line goes on for infinity, every x-value will be used for infinity. Therefore, the domain will be All Real Numbers since every number on the x-axis has a possibility of being used.
work out the area of this circle. take pi to be 3.142 and give your answer to be 2 decimal places. 11,2 cm
Answers
Answer:
11.2 i think so but you will write 11.2
(Irrational Numbers MC)
Approximate -10 + √30 to the nearest tenth. HELP PLS
Answers
-10 + 5.47722~
=4.523~
round to nearest tenth = 4.5
Answer:
-4.5
Step-by-step explanation:
\(\sqrt{30}\) is approximately 5.47722557505. You can find this number with a calculator.
-10 + 5.47722557505 = -4.52277442495
To add a negative and a positive number, you subtract the absolute values and take the sign of the number that has the larger absolute value. Absolute value just means thinking of both numbers as positive numbers.
Helping in the name of Jesus.
I need help pls help me
Answers
Answer:
Allison
Step-by-step explanation:
Allison:
2^6 = 64
Chris:
3³ = 27
Hannah:
4² = 16
Steve:
18^1 = 18
Answer:
Allison
Step-by-step explanation:
Allison
\(2^{6}\) = 2 x 2 x 2 x 2 x 2 x 2 = 64
Chris
\(3^{3}\) = 3 x 3 x 3 = 27
Hannah
\(4^{2}\) = 4 x 4 = 16
Steve
\(18^{1}\) = 18 = 18
An ice chest contains 9 cans of apple juice6 cans of grape juice5 cans of orange juiceand 4 cans of pineapple juice Suppose that you reach the container and randomly select three cans in successionFind the probability of selecting no grape juice Select one 243 506 6 17/45; c * 5/506; d * 102/253
Answers
Answer:
243/506
Step-by-step explanation:
There are 24 total juice boxes.
18 of them are not grape
You have an 18/24 chance of picking not grape juice
The second time, 1 is removed, then another is removed. This creates:
(18/24)*(18/23)*(18/22) = 243/506
Write an expression to represent the product of 6 and the square of a number plus 15. In your expression what is the value of the coefficient? A. 1 B. 6 C. 15 D. 2
Answers
Answer:
B) 6
Step-by-step explanation:
Let the number be x
Product of 6 and square of number plue 15 : (6x²) + 15
Coefficient of x² = 6
Solve the following linear equation using equivalent equations to isolate the variable. Express your answer as an integer, as a simplified fraction, or as a decimal number rounded to two places.
Answers
ANSWER
\(u=\frac{1}{5}\)EXPLANATION
We want to solve the given linear equation:
\(-6u=\frac{-6}{5}\)To do this, divide both sides of the equation by -6 to isolate u and simplify:
\(\begin{gathered} \frac{-6u}{-6}=\frac{-6}{5}\cdot\frac{1}{-6} \\ \Rightarrow u=\frac{1}{5} \end{gathered}\)That is the solution to the linear equation.
A transponder for a toll bridge costs $17.50. With the transponder, the toll is $5 each time you cross the bridge. The only other option is toll-by-plate, for which the toll is $7.25 each time you cross the bridge with an additional administrative fee of $1.25 for each crossing. How many times would you need to cross the bridge for the costs of the two toll options to be the same?
Answers
Answer: you would need to cross the bridge 5 times
Step-by-step explanation:
costing a total of $42.50 for each option.
hope this helps
Consider the parabola given by the equation:
f
(
x
)
=
−
2
x
2
−
8
x
+
14
Find the following for this parabola:
A) The value of
f
(
−
5
)
:
B) The vertex = (
,
)
C) The
y
intercept is the point (0,
)
D) Find the two values of
x
that make
f
(
x
)
=
0
. Round your answers to two decimal places. Write the values as a list, separated by commas:
x
=
Answers
Answer:
Sure, here are the answers to your questions:
**A) The value of $f(-5)$ is $-2$.**
To find the value of $f(-5)$, we can simply substitute $x=-5$ into the equation $f(x)=-2x^2-8x+14$. This gives us:
$$f(-5)=-2(-5)^2-8(-5)+14=-2(25)+40+14=-50+54=4$$
**B) The vertex of the parabola is $(2,6)$.**
To find the vertex of the parabola, we can complete the square. This involves adding and subtracting $\left(\dfrac{{b}}{2}\right)^2$ to both sides of the equation, where $b$ is the coefficient of the $x$ term. In this case, $b=-8$, so we have:
$$\begin{aligned}f(x)&=-2x^2-8x+14\\\\ f(x)+20&=-2x^2-8x+14+20\\\\ f(x)+20&=-2(x^2+4x)\\\\ f(x)+20&=-2(x^2+4x+4)\\\\ f(x)+20&=-2(x+2)^2\end{aligned}$$
Now, if we subtract 20 from both sides, we get the equation of the parabola in vertex form:
$$f(x)=-2(x+2)^2-20$$
The vertex of a parabola in vertex form is always the point $(h,k)$, where $h$ is the coefficient of the $x$ term and $k$ is the constant term. In this case, $h=-2$ and $k=-20$, so the vertex of the parabola is $(-2,-20)$. We can also see this by graphing the parabola.
[Image of a parabola with vertex at (-2, -20)]
**C) The $y$-intercept is the point $(0,14)$.**
The $y$-intercept of a parabola is the point where the parabola crosses the $y$-axis. This happens when $x=0$, so we can simply substitute $x=0$ into the equation $f(x)=-2x^2-8x+14$ to find the $y$-intercept:
$$f(0)=-2(0)^2-8(0)+14=14$$
Therefore, the $y$-intercept is the point $(0,14)$.
**D) The two values of $x$ that make $f(x)=0$ are $2.5$ and $-3.5$.**
To find the values of $x$ that make $f(x)=0$, we can set the equation $f(x)=-2x^2-8x+14$ equal to zero and solve for $x$. This gives us:
$$-2x^2-8x+14=0$$
We can factor the left-hand side of the equation as follows:
$$-2(x-2)(x-3)=0$$
This means that either $x-2=0$ or $x-3=0$. Solving for $x$ in each case gives us the following values:
$$x=2\text{ or }x=3$$
However, we need to round our answers to two decimal places. To do this, we can use the calculator. Rounding $x=2$ and $x=3$ to two decimal places gives us the following values:
$$x=2.5\text{ and }x=-3.5$$
Therefore, the two values of $x$ that make $f(x)=0$ are $2.5$ and $-3.5$.
Tommy is thinking of a number between 800 and 900 He divides it by 4 and there is a remainder of 1 He divides it by 5 and there is a remainder of 1 He divides it by 6 and there is a remainder of 1 He divides it by 7 and there is a remainder of 1
What is Tommy's number?
Answers
Answer:
841
Step-by-step explanation:
If the number is divided by 4 and the remainder is 1, the last digit must be 1, 3, 5, 7 or 9.
If the number is divided by 5 and the remainder is 1, the last digit must be 6 or 1.
So we already know the last digit must be 1.
The numbers between 800 and 900, with last digit 1, that divided by 6 have a remainder of 1 are:
811, 841, 871
The numbers between 800 and 900, with last digit 1, that divided by 7 have a remainder of 1 is just 841
So Tommy's number is 841.
Tommy's number is 841.
In this question we must determine first the least common number of 4, 5, 6 and 7, which is the product of these four numbers, that is to say:
\(x = 4\times 5\times 6 \times 7\)
\(x = 840\)
This is the least number that is divisible both for 4, 5, 6 and 7. Now we add this number by 1 to determine what number Tommy thought:
\(y = x + 1\)
\(y = 841\)
Tommy's number is 841.
To learn more on divisibility, we kindly invite to check the following verified question: https://brainly.com/question/369266
(sin30/1+cos30) + (1+cos30/sin30)
\( \sin(30 )\div 1 + \cos(30 ) + (1 + \cos(30 ) \div \sin(30) \)
Answers
Answer:
1
11111222223333334444554444667899ppojhgbsicudjejviwoiri3iw
Answer:
4
Step-by-step explanation:
\(\frac{sin 30}{1+cos 30} +\frac{1+cos 30}{sin 30} \\=\frac{sin 30(1-cos30)}{(1+cos30)(1-cos30)} +\frac{1+cos30}{sin 30} \\=\frac{sin30(1-cos30)}{1-cos^230 } +\frac{1+cos30}{sin 30} \\=\frac{sin 30(1-cos30)}{sin^2 30} +\frac{1+cos30}{sin30} \\=\frac{1-cos30}{sin30 } +\frac{1+cos30}{sin30} \\=\frac{1-cos30+1+cos 30}{sin 30} \\=\frac{2}{sin 30} \\=\frac{2}{\frac{1}{2} } \\=4\)
Indicate the range of the function. PLEEEAAASSEEEEE!!!!
Answers
Answer:
The right answer is D
(- infinite,6]
Write as the opposite of a square root. -3√5
Answers
The value of -3√5 as the opposite of the square root is -75.
What in mathematics is a square root?
The factor we can multiply by itself to obtain a given number is the number's square root.
Square root is represented by the symbol sqrt, which stands for square root of, end square root. Squaring an integer is the reverse of finding its square root.
-3√5
The opposite of the square root is the square, so,
-3√5 = -3 × 5²
-3√5 = - 3 × 25
-3√5 = - 75
Learn more about Square root
brainly.com/question/3120622
#SPJ1
need help with this ASAP
!!!!!!!!!!!!!!!!!!!!!!!!
Answers
The fence in dead center is about 399 feet from the third base.
What is the Pythagorean Theorem?The Pythagorean Theorem states that in the case of a right triangle, the square of the length of the hypotenuse, which is the longest side, is equals to the sum of the squares of the lengths of the other two sides.
Hence the equation for the theorem is given as follows:
c² = a² + b².
In which:
c > a and c > b is the length of the hypotenuse.a and b are the lengths of the other two sides (the legs) of the right-angled triangle.For the triangle in this problem, we have that:
The sides are d ft and 90 ft.The hypotenuse is of 409 ft.Hence the distance is obtained as follows:
d² + 90² = 409²
\(d = \sqrt{409^2 - 90^2}\)
d = 399 ft.
More can be learned about the Pythagorean Theorem at brainly.com/question/30203256
#SPJ1
17. the shaft is supported at its ends by two bearings a and b and is subjected to the forces applied to the pulleys fixed to the shaft. determine the resultant internal loadings acting on the cross section at point d. the 400-n forces act in the -z direction and the 200-n and 80-n forces act in the y direction. the journal bearings at a and b exert only y and z components of force on the shaft.
Answers
The resultant normal force at point D along the x-direction is \(F_D_x=0\) and the resultant shear force at point D along the y-direction is \(F_D_y=154.29N\)
Consider the equilibrium of the shaft.
Resolve the forces along the y-direction.
\(R_A_y+R_B_y=200+200+80+80R_A_y+R_B_y=560-----(1)\)
Take moments about point B and about the z-axis:
\(R_A_y*1.4=2*100*0.7+2*80*0.4\\\\R_A_y=245.71\)
Substitute the above value in equation (1).
\(245.71+R_B_y=560\\\\R_B_y=314.29N\)
Resolve the forces along the z-direction.
\(R_A_z+R_B_z=385+385R_A_z+R_B_z=770-----(2)\)
Take moments about point B and about the y-axis:
\(R_A_z*1.4=2*385*1.1\\\\R_A_z=605N\)
Substitute the above value in equation (2).
\(605+R_B_z=770\\\\R_B_z=165N\)
a) The resultant normal force at point D along the x-direction is
\(F_D_x=0\)
b) The resultant shear force at point D along the y-direction is
\(F_D_y-R_B_y+2*80=0\\\\F_D_y-314.29+160=0\\F_D_y=154.29N\)
To know more about the resultant normal forces:
https://brainly.com/question/14292810
#SPJ4
In 1998, the average price for bananas was 51 cents per pound. In 2003, the following 7 sample prices (in cents) were obtained from local markets:
50, 53, 55, 43, 50, 47, 58.
Is there significant evidence to suggest that the average retail price of bananas is different than 51 cents per pound? Test at the 5% significance level.
Answers
Answer:
\(t=\frac{50.857-51}{\frac{5.014}{\sqrt{7}}}=-0.075\)
The degrees of freedom are given by:
\(df=n-1=7-1=6\)
The p value for this case would be given:
\(p_v = 2*P(t_6 <-0.075)=0.943\)
The p value for this case is lower than the significance level so then we have enough evidence to FAIL to reject the null hypothesis and we can conclude that the true mean is not significantly different from 51
Step-by-step explanation:
Info given
50, 53, 55, 43, 50, 47, 58.
We can calculate the sample mean and deviation with this formula:
\(\bar X=\frac{\sum_{i=1}^n X_i}{n}\)
\(s=\sqrt{\frac{\sum_{i=1}^n (X_i -\bar X)^2)}{n-1}}\)
represent the mean height for the sample
\(s=5.014\) represent the sample standard deviation for the sample
\(n=7\) sample size
represent the value that we want to test
\(\alpha=0.05\) represent the significance level for the hypothesis test.
t would represent the statistic (variable of interest)
\(p_v\) represent the p value
Hypothesis to test
We want to test if the true mean is equal to 51, the system of hypothesis would be:
Null hypothesis:\(\mu = 51\)
Alternative hypothesis:\(\mu \neq 51\)
The statistic is given by:
\(t=\frac{\bar X-\mu_o}{\frac{s}{\sqrt{n}}}\) (1)
Replacing we got:
\(t=\frac{50.857-51}{\frac{5.014}{\sqrt{7}}}=-0.075\)
The degrees of freedom are given by:
\(df=n-1=7-1=6\)
The p value for this case would be given:
\(p_v = 2*P(t_6 <-0.075)=0.943\)
The p value for this case is lower than the significance level so then we have enough evidence to FAIL to reject the null hypothesis and we can conclude that the true mean is not significantly different from 51
The interior angles of a polygon are in A.P. If the smallest angle is 100 o
and the common difference is 4 o
, find the number of sides ?
Answers
The polygon has 21 sides whose interior angle are in Arithmetic Progression (A.P.)
The interior angles of a polygon are in an arithmetic progression (A.P) if the difference between any two consecutive angles is constant. To find the number of sides in a polygon given its smallest angle and the common difference of its interior angles, we can use the formula:
n = (180° - smallest angle) / common difference + 1, where n is the number of sides in the polygon.
In this case, the smallest angle is 100° and the common difference is 4°, so the number of sides can be calculated as follows:
n = (180° - 100°) / 4° + 1 = (80°) / 4° + 1 = 20 + 1 = 21.
Therefore, the polygon has 21 sides. It is important to note that a polygon with 21 sides is called an icosikaihenagon, which is a highly unusual and exotic shape, as most polygons have a smaller number of sides.
Learn more about polygon :
https://brainly.com/question/24464711
#SPJ4
Tina pet sits to earn extra money. She charges a flat service fee of $20, plus $15 per day. If one of her customers spent less than $125, which of the following inequalities could be used to solve for x, the number of days the customer paid for pet sitting?
Answers
Therefore, **x < 7** is the inequality that may be utilized to find x
What is inequality?A mathematical statement known as an inequality compares two expressions using an inequality sign, such as (less than), > (greater than), or (less than or equal to).
For instance, the inequality x + 2 5 signifies that "x + 2 is less than 5".
Let x represent how many days the client paid for pet sitting.
$15 per day plus a $20 fixed service fee equals the total cost of pet sitting.
We are aware that the customer's purchase was under $125. Consequently, we can write:
20 + 15x < 125
Putting this disparity simply:
15x < 105
x < 7
To know more about inequality visit:
brainly.com/question/11536194
#SPJ1
Stock dividend: Investor Sarah Warren currently holds 400 shares of Nutri-Foods. The firm has 40,000 shares outstanding. The firm most recently had earnings available for common stockholders of $80,000, and its stock has been selling for $22 per share. The firm intends to retain its earnings and pay a 10% stock dividend. c. What proportion of the firm will Sarah own after the stock dividend? Explain your answer.
Answers
We know that
• Sarah holds 400 shares.
,• The firm has 40,000 shares.
,• The recent earnings are $80,000.
,• The stock has been selling for $22.
,• The firm intends to pay 10% of the dividend.
To find the proportion, we just have to divide the number of shares Sarah holds and the total number of shares the firm has. Take into account it is after the stock dividend. Observe that 10% of 400 is 40, so we have to divide 440 by 40,000.
\(\frac{440}{40,000}=0.011\)Then, we multiply by 100 to express in percentage.
\(0.011\cdot100=1.1\)Hence, the proportion is 1.1%.how many 3/10 size are in 3 wholes
Answers
Answer:
9/10
Step-by-step explanation:
multiply 3/10 by 3.
3/10 x 3/1 =
3x3/10x1 =
9/10
3 ÷ 3/10
3 • 10/3
30/3
10
Done.
Two student clubs were selling t-shirts and school notebooks to raise money for an upcoming school event. In the first few minut
notebooks, and made $19. Club B sold 1 t-shirt and 1 notebook, for a total of $8.
-
Use matrices to solve the equation and determine the cost of a t-shirt and the cost of a notebook. Show or explain all necessary:
Answers
Using matrices the simultaneous equation is solved to get x = 3 and y = 5
How to solve the simultaneous equation using matricesThis method required finding determinants in three occasions then dividing
The given equation
\(\left[\begin{array}{cc}3&2&\\1&1\\\end{array}\right] \left[\begin{array}{c}x\\y\\\end{array}\right]= \left[\begin{array}{c}19\\8\\\end{array}\right]\)
the determinant is
\(\left[\begin{array}{cc}3&2&\\1&1\\\end{array}\right]\)
3 * 1 - 2 * 1 = 3 - 2 = 1
Solving for x
determinant while replacing x values
\(\left[\begin{array}{cc}19&2&\\8&1\\\end{array}\right]\)
19 * 1 - 2 * 8 = 19 - 16 = 3
solving for x = 3/1 = 3
Solving for y
determinant while replacing y values
\(\left[\begin{array}{cc}3&19&\\1&8\\\end{array}\right]\)
3 * 8 - 19 * 1 = 24 - 19 = 5
solving for y = 5/1 = 5
Learn more about simultaneous equations at:
https://brainly.com/question/148035
#SPJ1
find the mean of data set between 1-26?
Answers
Answer:
13
Step-by-step explanation:
13 is the number in the very middle of the set.
Another way to find this is to add up all numbers and divide by the total in the data set which in this case would be 26
what is the sum 3/x+9+5/x-9
Answers
Answer:
\(\frac{8}{x}\)
Step-by-step explanation:
what is the sum 3/x+9+5/x-9
\(\frac{3}{x} + 9 + \frac{5}{x} - 9 =\) (add \(\frac{3}{x}\) and \(\frac{5}{x}\))
\(\frac{8}{x} + 9 - 9 =\) (solve 9 - 9 = 0)
\(\frac{8}{x}\) ( your answer)
Sunset Lake is stocked with 2800 rainbow trout and after 1 year the population has grown to 7000. Assuming logistic growth with a carrying capacity of 28000, find the growth constant kk, and determine when the population will increase to 14600.
Answers
The growth constant is 1.0986 and the trout population will increase to 14600 after 2.1 years. The result is obtained by using the logistic equation.
How to find the increase of population?The increase of population can be found by using the logistic equation. It is
\(P(t) = \frac{K}{1 + Ae^{-kt} }\)
Where
P(t) = population at time t (in years)K = carrying capacityA = (K- P₀)/P₀k = growth constant of proportionalityt = time (in years)Sunset Lake is stocked with the rainbow trout. We have
P₀ = 2800P(1) = 7000K = 28000Find the growth constant k and time t when P(t) = 14600!
A = (K - P₀)/P₀
A = (28000 - 2800)/2800
A = 25200/2800
A = 9
After 1 year, we have 7000 rainbow trout. The growth constant is
\(7000 = \frac{28000}{1 + 9e^{-k(1)} }\)
\(1 + 9e^{-k} = 4\)
\(9e^{-k} = 3\)
\(e^{-k} = \frac{1}{3}\)
k = - ln (1/3)
k = 1.0986
Use k value to find the time when the population will increase to 14600!
\(14600 = \frac{28000}{1 + 9e^{-1.0986t} }\)
\(1.9178 = 1 + 9e^{-1.0986t}\)
\(0.9178 = 9e^{-1.0986t}\)
\(\frac{0.9178 }{9} = e^{-1.0986t}\)
\(t = \frac{ln \: 0.10198}{-1.0986}\)
t = 2.078
t ≈ 2.1 years
It is in another 1.1 years after t = 1.
Hence, the growth constant k is 1.0986 the population will increase to 14600 when t is 2.1 years.
Learn more about increase of population here:
brainly.com/question/13060148
#SPJ4
a trapezoid is shown in the grid
Answers
Answer:
To prove that it is a trapezoid, remember that the definition of a trapezoid is a quadrilateral with exactly one pair of parallel sides. Therefore, to prove it is a trapezoid you must verify that one pair of sides is parallel. From algebra, remember that two lines are parallel if they have the same slope.
Solve the inequation x - 12 ≤ 3 - 2x and graph its solution.
Let's do these one-by-one.
The solution to x - 12 ≤ 3 - 2x is:
Answers
Answer:
Step-by-step explanation:
x - 12 ≤ 3 - 2x
3x ≤ 15
x ≤ 5
To graph this, just draw a VERTICAL line passing through x = 5, then shade the area to the LEFT
FIGURE 1
FIGURE 2
7 cm
17 cm
FORMULA
PLUG IN
VALUES
3 cm
2 cm
VOLUME
10 cm
Total Volume:
Answers
CLICK TO REPORT