If f(x)=3x-1 and g(x)=x+2, find (f-g)(x)
Answers
Answer:
2x - 3
Step-by-step explanation:
\(f(x) = 3x - 1 \\ g(x) = x + 2 \\ (f - g)(x) = f(x) - g(x) \\ = 3x - 1 - (x + 2) \\ = 3x - 1 - x - 2 \\ = 3x - x - 1 - 2 \\ (f - g)(x) = 2x - 3\)
Related Questions
List in order from least to greatest.

Answers
Answer:
56%, 4/5, 1.07, 5/4
Step-by-step explanation:
5/4=1.25
56%=0.56
1.07
4/5=0.8
so the order is
56%, 4/5, 1.07, 5/4
let s(n) denote the number of steps required to carry out a certain algorithm with n items being processed. foreach function, describe what happens to s(n) if n is doubled
Answers
If the algorithm has a constant number of steps independent of the input size, s(n) remains the same when n is doubled.
Then the effect on the number of steps required, denoted as s(n), when the number of items being processed (n) is doubled will depend on the specific algorithm and its complexity.
Here are a few possibilities:
1. Constant Time Complexity (O(1)): If the algorithm has a constant time complexity, it means that the number of steps required remains the same, regardless of the input size. In this case, doubling n would not have any impact on s(n).
2. Linear Time Complexity (O(n)): If the algorithm has a linear time complexity, it means that the number of steps required is directly proportional to the input size. Doubling n would approximately double the number of steps as well. Thus, s(n) would increase in a linear manner.
3. Quadratic Time Complexity (O(n^2)): If the algorithm has a quadratic time complexity, it means that the number of steps required grows quadratically with the input size. When n is doubled, the number of steps would be approximately four times the original amount. Thus, s(n) would increase significantly.
4. Logarithmic Time Complexity (O(log n)): If the algorithm has logarithmic time complexity, doubling n would not have a substantial impact on the number of steps required. The increase in s(n) would be relatively small compared to the increase in n.
These are just a few examples, and there are various other complexities that algorithms can exhibit.
Each algorithm has its own time complexity, which determines how the number of steps required changes as the input size is doubled.
To know more about algorithms refer here:
https://brainly.com/question/31936515#
#SPJ11
the question is long so I will send a pic lol <3

Answers
Explanation
Step 1
let x represents the year
let y represents the hours of electricity generated ( in millons)
then, we have two coordinates of the function
\(undefined\)use the vectors in the figure below to graph the following vector

Answers
Given:
The given vector is w.
Required:
We need to draw 3w.
Explanation:
Use the Pythagorean theorem to find the magnitude AB.
Let the origin be (0,0).
Point A is (0,4) and point B is (3,0).
The magnitude of AB is (3-0,0-4)
\(w=(3,-4)\)Multiply the equation by 3 to find 3w.
\(3\cdot w=3\cdot(3,-4)\)\(3w=(3\cdot3,3\cdot(-4))\)\(3w=(9,-12)\)Consider any point on the graph and take it as the origin (0,0) and mark (9,-12) and joint them as follows.
Final answer:


Help me plzz I don’t understand this question I have 15min left




Answers
Answer:
1) 150°
2) 30°
3) 50°
4) 70°
5) 100°
Find the greatest common factor.
3x^2a+3xa^2
Answers
Since
3
x
2
a
,
3
x
a
2
contain both numbers and variables, there are two steps to find the GCF (HCF). Find GCF for the numeric part then find GCF for the variable part.
Steps to find the GCF for
3
x
2
a
,
3
x
a
2
:
1. Find the GCF for the numerical part
3
,
3
2. Find the GCF for the variable part
x
2
,
a
1
,
x
1
,
a
2
3. Multiply the values together
Find the common factors for the numerical part:
3
,
3
The factors for
3
are
1
,
3
.
Tap for more steps...
1
,
3
The factors for
3
are
1
,
3
.
Tap for more steps...
1
,
3
List all the factors for
3
,
3
to find the common factors.
3
:
1
,
3
3
:
1
,
3
The common factors for
3
,
3
are
1
,
3
.
1
,
3
The GCF for the numerical part is
3
.
GCF
Numerical
=
3
Next, find the common factors for the variable part:
x
2
,
a
,
x
,
a
2
The factors for
x
2
are
x
⋅
x
.
x
⋅
x
The factor for
a
1
is
a
itself.
a
The factor for
x
1
is
x
itself.
x
The factors for
a
2
are
a
⋅
a
.
a
⋅
a
List all the factors for
x
2
,
a
1
,
x
1
,
a
2
to find the common factors.
x
2
=
x
⋅
x
a
1
=
a
x
1
=
x
a
2
=
a
⋅
a
The common factors for the variables
x
2
,
a
1
,
x
1
,
a
2
are
x
⋅
a
.
x
⋅
a
The GCF for the variable part is
x
a
.
GCF
Variable
=
x
a
Multiply the GCF of the numerical part
3
and the GCF of the variable part
x
a
.
3
x
a
Answer: 3xa
Step-by-step explanation:
Find the prime factors of each term in order to find the greatest common factor
find the missing side length when the perimeter is 20
Answers
Answer:
the answer is 5 here you go
"Find an equation for the line tangent to the curve at the point defined by the given value of t. Also, find the value of d²y / dx² at this point. x = 4 cos t, y = 4 sint, t = - π / 4
Answers
The line tangent to the curve defined by x = 4cos(t), y = 4sin(t) at t = -π/4 is y = -x - 2√2, and the value of d²y/dx² at that point is -1.
To find the equation of the tangent line, we need to determine the slope of the curve at the given point.
We can calculate the derivative of y with respect to x using the chain rule: dy/dx = (dy/dt) / (dx/dt). For x = 4cos(t) and y = 4sin(t), we have dx/dt = -4sin(t) and dy/dt = 4cos(t). At t = -π/4, dx/dt = -4/√2 and dy/dt = 4/√2. Therefore, the slope of the tangent line is dy/dx = (4/√2) / (-4/√2) = -1.
Using the point-slope form of a line, we obtain y - 4sin(-π/4) = -1(x - 4cos(-π/4)), which simplifies to y = -x - 2√2. The second derivative d²y/dx² represents the curvature of the curve. At the given point, d²y/dx² = -1, indicating a concave shape.
Learn more about Equation click here :brainly.com/question/13763238
#SPJ11
Please solve this question

Answers
Answer:
46?
Step-by-step explanation:
23*2=46
Answer:
37.31 cm
Step-by-step explanation:
∡ AB = 180 - 148 = 32° = ∡ DE
∡ CD = 360 - ∡ AE - ∡ AB - ∡ BC - ∡ DE = 360 - 148 - 32 - 87 - 32 =61°
∡ CE = 61 + 32 = 93°
arc length = 2\(\pi\)r \(\frac{angle}{360}\) = 2×3.14×23×\(\frac{93}{360}\\\) = 37.31 cm
Someone please answer my question

Answers
Answer:
Point D is the solution to the system of equations.
Step-by-step explanation:
When asked for a solution involving 2 equations, the goal is to find a point (x,y) that would be a solution to both equations. Any point on a line that is defined by an equation is a solution to that equation. For an equation of y = 2x + 2, possible solutions are (1,4), (2,6), (5,12) etc. These points all lie on the line formed by that equation. There are an infinite number of possible solutions. If a second eqaution is added, there is now a constraint on the possible answers. The goal is to find a point that satisfies both equations.
If a seond equation of y = 1x + 3 were matced with y=2x+2, both are straight lines, but with different slopes. So they will intersect at some point. One may either solve mathematically using substitution, or by graphing, as was done here.
Matematically:
y = 2x + 2
y = 1x + 3
Rearrange either equation to isolate a variable, x or y. These are already isolated (since I made them up) so go to the next step of substituting one expression of y into the other:
y = 1x + 3
2x + 2 = 1x + 3
x = 1
Now use this value of x to find y:
y = 2x + 2
y = 2*(1) + 2
y = 4
The point these two lines intersect is (1,4) and is the "solution" to this series of equations.
See the attached graph.
not sure how to do this can you help me ?

Answers
Here , we are going to use Trigonometric ratios.
In given right angled ∆ ;
\({:\implies \quad \sf \dfrac{x}{18}=\sin (60^{\circ}) \quad \bigg\{ \because \sin (\theta)=\dfrac{P}{H}\bigg\}}\)
\({:\implies \quad \sf x=\dfrac{18\sqrt{3}}{2} \quad \bigg\{\because \sin (60^{\circ})=\dfrac{\sqrt{3}}{2}\bigg\}}\)
\({:\implies \quad \bf \therefore \quad x=9\sqrt{3} \: units}\)
Also;
\({:\implies \quad \sf \dfrac{y}{18}=\cos (60^{\circ}) \quad \bigg\{ \because \cos (\theta)=\dfrac{B}{H}\bigg\}}\)
\({:\implies \quad \sf x=\dfrac{18}{2} \quad \bigg\{\because \cos (60^{\circ})=\dfrac{1}{2}\bigg\}}\)
\({:\implies \quad \bf \therefore \quad y=9 \: units}\)
Hence , The required values for x and y are 9√3 and 9 units
Porfa es para un examen xD

Answers
Answer: -13
Step-by-step explanation:
M(3) → x = 3M(2) → x = 2\(\frac{M(3)+M(2)}{2} =\frac{[-2(3)^{2}] +[-2(2)^{2}]}{2}=\frac{(-2)(9)+(-2)(4)}{2}=\frac{-18-8}{2}=\frac{-26}{2}=-13\)

A sheet of plastic has an area of 35 square cm. If the sheet is 5 cm thick, what is the volume?
Answers
Answer:
175 cm³
Step-by-step explanation:
Volume = área * thick
Volume = 35cm² * 5cn
Volume = 175 cm³
Answer:
7cm
Step-by-step explanation:
Area = 35cm²
Length= 5cm
Width=?
A=L×B
B=A/L
B=35/5
B=7cm
Someone please help with my STAT homework PLEASE I will give brainliest

Answers
Hi there!
a. A stratified sample can be used by dividing the tenants into two groups: those who have children and those who do not have children. Then, a Sample Random Sample FROM EACH stratum can be conducted for a total of 16 tenants surveyed.
b. Using a cluster sample in this situation could introduce undercoverage or selection bias if there is a distinction between those on some floors and those on others. For example, tenants on lower floors might be more opposed to a playground (ex: noise, crowd, etc.) in comparison to those on higher floors.
typically, in which type of claim is it most important to have a random sample?
Answers
It is most important to have a random sample in inferential statistics, particularly in making statistical inferences about a population based on the sample data.
Random sampling is a critical component of inferential statistics because it helps to ensure that the sample is representative of the population. When a sample is randomly selected, each member of the population has an equal chance of being included in the sample, which reduces the risk of bias in the results. Without a random sample, the results of statistical analyses may not be accurate or generalizable to the population, and the conclusions drawn from the data may be flawed or misleading.
Therefore, random sampling is crucial in making valid statistical inferences about a population.
Learn more about Random Sampling here: brainly.com/question/30759604
#SPJ11
. In which quadrant does θ lie given that sinθ>0 and cosθ<0?
Quadrant I
Quadrant II
Quadrant III
Quadrant IV
Answers
Answer:
Quadrant II
Step-by-step explanation:
Which linear inequality is represented by the graph?
y<3x+2
y>3x+2
y<1/3x+2
y>1/3x+2

Answers
Answer:
Y < 3x+2
Step-by-step explanation:
Alright so if you ever get stuck on something like this, Go on demos and put in (0,2) and then add in (-3,-7) and then add in the other answers to see if they match.
So your answer is:
y>3x+2

what is the first step in evaluating the expression shown below? will send image.
Answers
Using PEMDAS
We must first clear P which stands for Parentheses
The values in the parentheses are (12.9 -3.1)
so the first and right option is option c subtract 3.1 from 12.9
An SRS of 20 orangutans is selected, and 65 cc of blood is to be drawn from each orangutan using a 100 cc syringe. In the sample, the mean volume is 64 cc and the standard deviation is 12 cc. Assume that in the population of all such procedures, the amount of blood drawn follows a Normal distribution with mean ?.
Reference: Ref 17-1
We are interested in a 95% confidence interval for the population mean volume. The margin of error associated with the confidence interval is
Answer
A. 4.64.
B. 2.68.
C. 6.84.
D. 5.62.
Answers
The margin of error associated with the 95% confidence interval for the population mean volume is: D. 5.62.
To calculate the 95% confidence interval for the population mean volume, we can use the formula:
CI = x ± (t * (s/√n))
Where CI represents the confidence interval, x is the sample mean, t is the t-score associated with the desired confidence level (95%), s is the sample standard deviation, and n is the sample size.
In this case, x = 64 cc, s = 12 cc, and n = 20 orangutans. We need to find the t-score for a 95% confidence interval with 19 degrees of freedom (n-1). Using a t-table, we find that the t-score is approximately 2.093.
Now we can calculate the margin of error:
Margin of Error = t * (s/√n) = 2.093 * (12/√20) ≈ 5.62
Therefore, the margin of error associated with the 95% confidence interval for the population mean volume is: D. 5.62.
Visit here to learn more about margin of error brainly.com/question/29419047
#SPJ11
which ratio is equivalent to 4:10? Choose ALL the equivalent ratios
Answers
Answer:
2:5
12:30
Step-by-step explanation:
How would you describe the shape of the normal distribution?
Answers
The shape of the normal distribution is bell shape and it is also symmetrical from the left and right sides about the origins (mean).
What is a normal distribution?
A normal distribution is a function on some random variables, which represent the set of all those random variables in a symmetrical bell shape about the mean value.
It shows that the probability of occurrence of some data which is distributed over a function is more at or around the mean.
It is also known as probability distribution curve.
The normal distribution has two parameters:
MeanStandard deviationWhat is the shape of the normal distribution?
The normal distribution curve is at it's peak at the mean value. This shows that the probability of occurrence of the data or value is more concentrated or distributed about the mean. It is also symmetric about the mean. As we more further from the mean, we see that the normal distribution curve gradually decreases showing that the probability of occurrence of the data or the values decreases. The shape that this curve forms is like a bell-shaped. So the shape of normal distribution is bell shape.
Hence, the shape of the normal distribution is bell shape and it is also symmetrical from the left and right sides about the origins (mean).
Know more about "normal distribution" here: https://brainly.com/question/15103234
#SPJ4

What are the numerical measures of each angle in the diagram? 1 and 3 measure degrees. 2 and 4 measure degrees. (3x - 1)º (2x + 9)°
Answers
Answer:
Step-by-step explanation:
In the diagram shown, the measure of angle 1 is oppositely directed to angle 2 and oppositely directed angles are equal.
Hence <1 = <3
Given < 1 = 3x-1 and <3 = 2x+9
Hence 3x-1 = 2x+9
collect like terms
3x-2x = 9+1
x = 10°
Since <1 = 3x-1
on substituting x = 10
<1 = 3(10)-1
<1 = 30-1
<1 = 29°
<1+<2 = 180 (angle on a straight line)
29+<2 = 180
<2 = 180-29
<2 = 151°
Similarly, on substituting x = 10 into <3
<3 = 2x+9
<3 = 2(10)+9
<3 = 20+9
<3 = 29°
<3+<4 = 180 (angle on a straight line)
29+<4 = 180
<4 = 180-29
<4 = 151°

Answer:
keeping it simple answers are 29 and 151 now thats simple
Step-by-step explanation:
Mikki created a painting with an area of 32 square feet and a length of 4 feet. They create a second painting with an area of 24 square feet. It has the same width as the first painting. what is the length of the second painting?
Answers
Answer:
3 feet
Step-by-step explanation:
To begin, find the width of the first painting by dividing 32 by 4. You get 8 feet as the width. Since the second painting has a width of 8, divide 24 by 8 to get the length (area of a rectangle is length times width). You get that the length of the second painting is 3 feet.
Hopefully this helps- let me know if you have any questions!
The circumference of a circle is 19π ft. What is the area, in square feet? Express your answer in terms of \piπ
Answers
Answer:
1134.1 [cm²]
Step-by-step explanation:
A=πr2
Circle area = π * r² = π * 361 [cm²] ≈ 1134.1 [cm²]
π ≈ 3.14159265 ≈ 3.14
d = r * 2 = 19 [cm] * 2 = 38 [cm]
Remember y=mx +b Given the following graph what would the equation be?

Answers
Answer:
y=5/3x
Step-by-step explanation:
since the line crosses the y intercept at 0, nothing needs to be there. The 5/3 is from rise/run, so 5 up and 3 right
Answer:
a. y = 5/3x
Step-by-step explanation:
Since the line passes through the origin, there is no y-intercept so we can eliminate B and D. Now let's find two points on the graph;
(-3, -5) and (0, 0)
Find the slope using the formula [ y2-y1/x2-x1 ]
0-(-5)/0-(-3)
5/3
Input this into the slope-intercept form expression and we have our answer.
y = 5/3x
Best of Luck!
Question 3 - Simulating a Random Walk
Consider the following random process:
You start at point zero and take a number of steps. Each step is
equally likely to be a step forward (+1) or a step backwar
Answers
Answer:
The random process described is a symmetrical random walk.
A symmetrical random walk is a mathematical model that represents a series of steps taken in either a forward (+1) or backward (-1) direction, each with equal probability. Starting from point zero, the process involves taking a certain number of steps. The outcome at each step is independent of previous steps, making it a stochastic process. The key characteristic of a symmetrical random walk is that, on average, the process remains centered around its starting point. This means that over a large number of steps, the expected displacement from the starting point approaches zero.
Learn more about: Random walks
brainly.com/question/28534847
#SPJ11
Use the functions to find the expected number of plants in 10 years for each method
Answers
Part A: For the method of buying new bulbs each year: new_bulbs(year): return 50*year + 6
Part B: we expect to have 506 plants if we buy new bulbs each year and 6144 plants if we divide existing bulbs after 10 years.
Part C: For the method of buying new bulbs each year: new_bulbs(5) = 256 new_bulbs(15) = 756
Part A:
Let's define two functions to model the expected number of plants for each year:
For the method of buying new bulbs each year:
new_bulbs(year):
return 50*year + 6
For the method of dividing existing bulbs:
divide_bulbs(year):
return 6*(2**year)
Part B:
To find the expected number of plants in 10 years for each method, we simply need to evaluate the functions at year = 10:
For the method of buying new bulbs each year:
new_bulbs(10) = 506
For the method of dividing existing bulbs:
divide_bulbs(10) = 6144
Therefore, we expect to have 506 plants if we buy new bulbs each year and 6144 plants if we divide existing bulbs after 10 years.
Part C:
To compare the expected number of plants in five years to the expected number of plants in 15 years, we can evaluate the functions at year = 5 and year = 15:
For the method of buying new bulbs each year:
new_bulbs(5) = 256
new_bulbs(15) = 756
For the method of dividing existing bulbs:
divide_bulbs(5) = 96
divide_bulbs(15) = 32768
We can see that the expected number of plants for both methods increases significantly between 5 and 15 years, but the method of dividing existing bulbs shows a much greater increase. This is because each year, the gardener can double the number of plants by dividing the existing bulbs. In contrast, the number of plants obtained by buying new bulbs increases linearly.
These patterns could affect the method the gardener decides to use depending on their goals and resources. If the gardener wants to have a larger number of plants in the short term (i.e., within five years), buying new bulbs each year may be a better option. However, if the gardener wants to have a larger number of plants in the long term (i.e., beyond five years), dividing existing bulbs may be more efficient and cost-effective. If the gardener has limited resources, dividing existing bulbs may be a more sustainable option as it allows them to multiply their existing plants without having to buy new bulbs every year.
Learn more about mathematics here: brainly.com/question/24600056
#SPJ4
Complete question is in the image attached below

if g(x)=x^2-6x+9 which statements are true
Answers
The true statements about the function \(g(x) = x^2 - 6x + 9\) are that it is a quadratic function, it opens upwards, and it has a minimum point.
To determine the true statements about the function \(g(x) = x^2 - 6x + 9,\)we can analyze its properties and characteristics.
The function is a quadratic function: True.
The expression\(g(x) = x^2 - 6x + 9\) represents a quadratic function because it has a degree of 2.
The function opens upwards: True.
Since the coefficient of \(x^2\) is positive (1), the parabola opens upwards.
The vertex of the parabola is at the minimum point: True.
The vertex of a quadratic function in the form \(ax^2 + bx + c\) is given by the formula x = -b/2a.
In this case, the vertex occurs at x = -(-6)/(2\(\times\)1) = 3.
Substituting x = 3 into the function, we find g(3) = 3^2 - 6(3) + 9 = 0. Therefore, the vertex is at (3, 0), which represents the minimum point of the parabola.
The parabola intersects the x-axis at two distinct points: True. Since the coefficient of \(x^2\) is positive, the parabola opens upwards and intersects the x-axis at two distinct points.
The function has a maximum value: False.
Since the parabola opens upwards, the vertex represents the minimum point, not the maximum.
The function is always increasing: False.
The function is not always increasing since it is a quadratic function. It increases to the left of the vertex and decreases to the right of the vertex.
In summary, the true statements about the function \(g(x) = x^2 - 6x + 9\) are:
The function is a quadratic function.
The function opens upwards.
The vertex of the parabola is at the minimum point.
The parabola intersects the x-axis at two distinct points.
The function is not always increasing.
For similar question on quadratic function.
https://brainly.com/question/1214333
#SPJ8
Regular hexagon ABCDEFG in inscribed into circle O and AB=8cm. Calculate each of the following:
(a)What is the radius of circle O
(b)What is the area of circle O
(c)What is m
(d)What is m
(e)What is the measure of arc AB
(f)What is the measure of arc ACE
(g)What is the length of arc AB
(h)What is the area of sector AOB
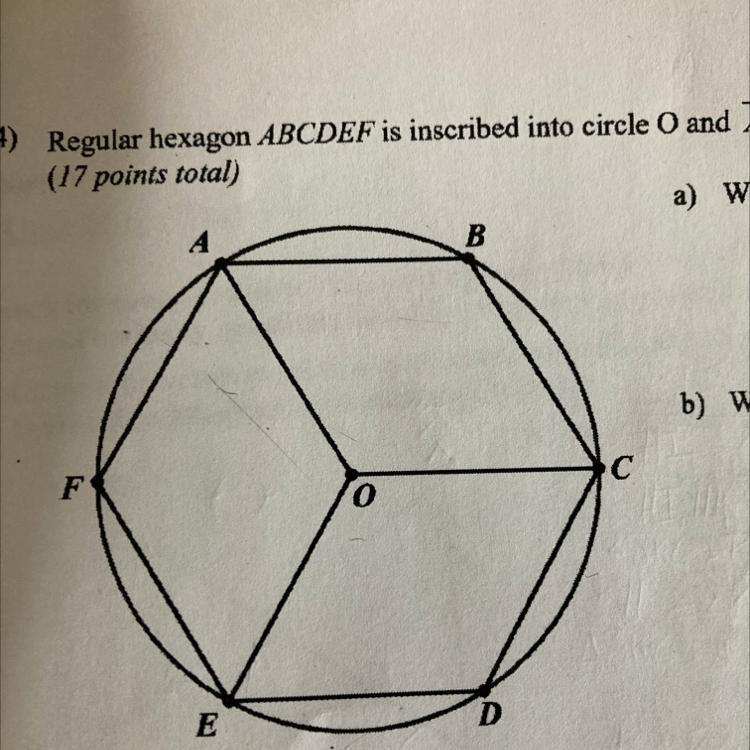
Answers
a. The radius of the circle O is 8 cm.
c. The circle has an area of 213.66 square centimeters.
e. AB's arc length equals 60 degrees
f. ACE has arc measure of 240 degree.
g. the arc length is 8.38 cm
h. area of the sector AOB is 33.51 cm²
How to find the radius of the circlea. The radius of the circle is solved using the properties of a regular hexagon
It has equal sides and angles on all six sides.There is a 120° inside angle and a 60° outside angle.There are six equilateral triangles in it.The radius is 8 cm since the base of one of the equilateral triangles is the radius.
b. Area of circle O
= 3.142 * 8^2
= 213.66 squared cm
e. measure of arc AB
The center angle that creates the intercepted arc is what is known as the arc measure, which is measured in degrees.
= 60 degrees
f. measure of arc ACE
= arc AB + arc BC + arc CD + arc DE
= 60 + 60 + 60 + 60
= 240 degrees
g. length of arc AB
= 60/360 * 2 * 3.142 * 8
= 8.38 cm
h. area of the sector AOB
= 60/360 * 3.142 * 8²
= 33.51 cm²
Learn more about length of arc at:
https://brainly.com/question/8020286
#SPJ1
In public opinion surveys, a sample of the total population
a. must be at least 50 percent of the targeted population.
b. need be only 25 percent of the targeted population.
c. need be only 10 percent of the targeted population.
d. must be representative in that the views of those in the sample must accurately and proportionately reflect the views of the whole population.
e. must be based on all the registered voters in the targeted population.
Answers
In order for a sample of the entire population to be considered representative in public opinion polls, it must correctly and fairly reflect the views of the entire population.
Public opinion surveys are used to collect data and information on the opinions and views of people in a given population. For the results of a survey to be valid and reliable, the sample of people chosen for the survey must be representative of the entire population. This means that the views of those in the sample must accurately and proportionately reflect the views of the whole population.
Public opinion surveys are designed to measure the opinions and views of people in a given population. To ensure the results of the survey are accurate and reliable, the sample of people chosen for the survey must be representative of the entire population. This means that the views of those in the sample must accurately and proportionately reflect the views of the whole population. It is not necessary for the sample to exceed 50% of the targeted population, nor does it need to be based on all registered voters in the population. Therefore, option d. is the correct answer, which states that the sample must be representative in that the views of those in the sample must accurately and proportionately reflect the views of the whole population.
Learn more about population here
https://brainly.com/question/19538277
#SPJ4