If f(x) = x³ + 14x² + 61x + 84, which of the following is not a factor of f(x)?
Answers
Related Questions
If Susan will be 2 times old in seven years as she was 3 years ago, what is Susan's present age?
Answers
Answer:
Let's start by assigning a variable to Susan's present age. Let's call it "x".
According to the problem, in seven years, Susan will be "x + 7" years old.
Three years ago, Susan was "x - 3" years old.
The problem tells us that Susan will be 2 times as old in seven years as she was 3 years ago. So we can set up the following equation:
x + 7 = 2(x - 3)
Now we can solve for x:
x + 7 = 2x - 6
x = 13
Therefore, Susan's present age is 13 years old.
Let's assume Susan's present age is "x" years. According to the information provided, "Susan will be 2 times old in seven years as she was 3 years ago."
Seven years from now, Susan's age would be x + 7, and three years ago, her age would have been x - 3. According to the given statement, her age in seven years will be two times her age three years ago:
x + 7 = 2(x - 3)
Let's solve this equation to find Susan's present age:
x + 7 = 2x - 6
Subtracting x from both sides:
7 = x - 6
Adding 6 to both sides:
13 = x
Therefore, Susan's present age is 13 years.
Simplify. Your answer should contain only positive exponents.
2*2^-3
Answers
The parent function (x) = x3 is represented by graph A. Graph A is transformed to get graph B and graph C. Write the functions represented bygraph B and graph C.Graph B represents the function g(x)=Graph C represents the function /x)=
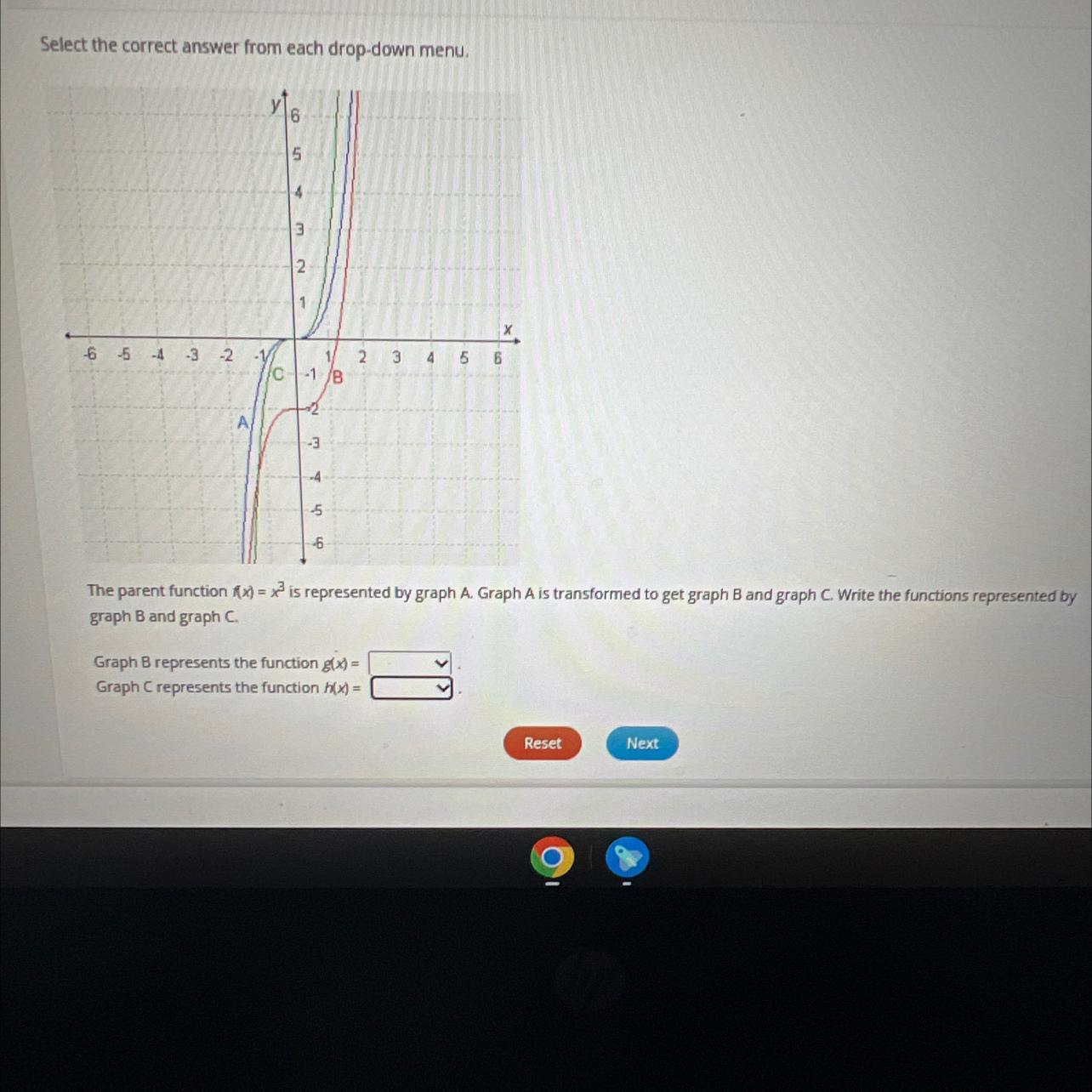
Answers
Given:
The parent function is
\(f(x)=x^3\)represented by graph A. Graph A is transformed to get graph B and graph C.
Required:
To find the function B and C by using the graph.
Explanation:
The graph B represents the function g(x) :
Here the graph shifts 2 units down.
So
\(g(x)=x^3-2\)The graph C represents the function h(x) :
Here the transformed function have horizontal compression of 2 units.
\(h(x)=2x^3\)Final Answer:
\(\begin{gathered} g(x)=x^3-2 \\ h(x)=2x^3 \end{gathered}\)A box has a width of 10 cm and a length of 17 cm. The volume of the box is decreasing at a rate of 527 cubic cm per minute, with the width and length being held constant. What is the rate of change, in cm per minute, of the height when the height is 6 cm?
Round your answer to the nearest hundredth. (Do not include any units in your answer.)
Answers
Therefore, the rate of change, in cm per minute, of the height when the height is 6 cm is approximately -6 cm/min.
Given,The width of the box = 10 cm Length of the box = 17 cmThe volume of the box = 527 cubic cm/minWe need to find the rate of change, in cm per minute, of the height when the height is 6 cm.We know that the volume of the box is given as:V = l × w × h where, l, w and h are length, width, and height of the box respectively.It is given that the width and length are being held constant.
Therefore, we can write the volume of the box as
:V = constant × h Differentiating both sides with respect to time t, we get:dV/dt = constant × dh/dtNow, it is given that the volume of the box is decreasing at a rate of 527 cubic cm per minute.
Therefore, dV/dt = -527.Substituting the given values in the above equation, we get:
527 = constant × dh/dt
We need to find dh/dt when h = 6 cm.To find constant, we can use the given values of length, width and height.Substituting these values in the formula for the volume of the box, we get:
V = l × w × hV = 17 × 10 × hV = 170h
We know that the volume of the box is given as:V = constant × hSubstituting the value of V and h, we get:
527 = constant × 6 cm
constant = 87.83 cm/minSubstituting the values of constant and h in the equation, we get
-527 = 87.83 × dh/dtdh/dt = -6.0029 ≈ -6 cm/min
For such more question on Length
https://brainly.com/question/28108430
#SPJ8
An IQ test is designed so that the mean is 100 and the standard deviation is 15 for the population of normal adults. Find the sample size necessary to estimate the mean IQ score of the residents of a state if you want to be 95% confident that the sample mean is within 4 IQ points of the true mean.
What is the required sample size?
Answers
Answer:
55
Step-by-step explanation:
\(\displaystyle MOE = z\biggr(\frac{\sigma}{\sqrt{n}}\biggr)\\\\4=1.96\biggr(\frac{15}{\sqrt{n}}\biggr)\\\\4=\frac{29.4}{\sqrt{n}}\\\\\sqrt{n}=\frac{29.4}{4}\\\\\sqrt{n}=7.35\\\\n=54.0225\\\\n\approx55\uparrow\)
Make sure to always round up the required sample size to the nearest integer!
Which of the following is equivalent to the product below?
Square root 3 square root 21
I NEED HELP ILL GIVE BRAINLIEST
Answers
The equivalent of the products given = 3√7
Simplifying square rootsA perfect square root is said to be a number that gives rise to an integer when it's square root is carried out. Examples are √16, √9 which is 4 and 3 respectively.
√3 × √21
But √a ×√b = √ a×b
Find the prime factors which when multiplied would give 21 = 3 and 7.
Therefore,
\( \sqrt{3 \times 3 \times 7} \)
\( \sqrt{9 \times 7} \)
\( 3 \sqrt{7} \)
Therefore, the equivalent of the products of √3 × √21 =
3√7
Learn more about perfect square roots here:
https://brainly.com/question/3617398
Urgent!!!!!!!!!!!!!!!!!!!

Answers
Answer:
4+2/3-1 = 3
Step-by-step explanation:
hopefully it helped
Solve y = ax² + c for x.
O x
x= ± √ay-c
O
O
x = ±₁
X=
X=
у-с
a
y
y + c
a

Answers
In the quadratic equation y = a\(x^{2}\) + c ,the value of x = ± \(\sqrt \frac{y-c}{a}\)
A quadratic equation is any equation containing one term wherein the unknown is squared and no term wherein it's far raised to a higher power.
A quadratic equation is an algebraic equation of the second degree in x. The quadratic equation in its standard form is ax2 + bx + c = 0, in which a and b are the coefficients, x is the variable, and c is the constant term.
To find the value of x
Assuming \(a\neq o\)
First, subtract c from both the sides to get:
\(y-c=ax^{2}\)
then, divide both sides by \(a\) and transpose to get:
\(x^{2} =\frac{y-c}{a}\)
So, \(x\) must be a square root of \(\frac{y-c}{a}\) and we can deduce:
\(x=\) ± \(\sqrt \frac{y-c}{a}\)
Learn more about quadratic equations here brainly.com/question/1214333
#SPJ9
Which shape has only one pair of parallel sides?

Answers
Answer:
The answer is C.
Step-by-step explanation:
This is because that shape only has the top and bottom lines which are parallel. The sides are not vertical and leaning outwards, which are not parallel. Leaving that shape to only have one pair of parallel sides.
Answer:
C.
Step-by-step explanation:
A & B both have 2 pairs of parallel lines, so they're not a choice. D has three sides, making it a triangle. Meaning it has no pairs of parallel lines. That leaves us with C. The reason why C is the answer is because, we can see that both top and bottom lines are parallel to each other. However, the left and right lines are not.
I hope this helped!
Find a. Round your answer to the nearest hundredth

Answers
Step-by-step explanation:
\(c = 40 \\ b = 180 - 90 - 40 = 50\)
\( \cos(40) = \frac{a}{12} \\ 0.766 = \frac{a}{12 } \\ a = 9.19\)
Can someone please help awnser these.

Answers
The answers are 4. a) 15.7 cm, b) 26.25 m, 5. a) 128.74 cm, b) 40.82 mm, c) 45 cm and 6. 777.28 cm
Given are the circles and the circular items we need to find their circumference,
Circumference of a circle = 2π × radius = Diameter × π
4. a) Circumference = 5 × 3.14 = 15.7 cm
b) Circumference = 8.36 × 3.14 = 26.25 m
5. a) Circumference = 41 × 3.14 = 128.74 cm
b) Circumference = 13 × 3.14 = 40.82 mm
c) Circumference = 14.3 × 3.14 = 45 cm
6.
The perimeter of the cloth = circumference of the circular ends plus length in the middle,
= 76 × 2 × 3.14 + 150 × 2
= 477.28 + 300
= 777.28 cm
Learn more about Circumference click;
https://brainly.com/question/28757341
#SPJ1
54. f(x) = ln (x + 1)
What is the end behavior?
Answers
The function end behavior of ln(x + 1 ) is \(\quad \mathrm{as}\:x\to \:+\infty \:,\:f\left(x\right)\to \:+\infty \:\)
How to determine the end behavior of the functionFrom the question, we have the following parameters that can be used in our computation:
f(x) = ln(x + 1)
The end behavior of a function f(x) describes the behavior of the function as x approaches \(+\infty\) and as :x approaches \(-\infty\)
Calculate f(∝) and f(-∝)
So, we have
f(∝) = ln(∝ + 1) = +∝
f(-∝) = ln(-∝ + 1) = +∝
Using the above as a guide, we have the following:
The function end behavior of ln(x + 1 ) is \(\quad \mathrm{as}\:x\to \:+\infty \:,\:f\left(x\right)\to \:+\infty \:\)
Read more about end behavior at
https://brainly.com/question/1365136
#SPJ1
find the area of ABC

Answers
Answer:
area of ABC=1/2 b×h=1/2×20×6=30m²
Answer:
60 m^2
Step-by-step explanation:
( Base * Hight / 2 = Area)
20 * 6 = 120
120 / 2 = 60
A game require rolling a six sided die numbered fro 1 to 6. What is the probability of rolling a 1 or a 2?
Answers
Answer:
1/3
Step-by-step explanation:
hello,
probability of 1 = 1/6
probability of 2 = 1/6
probability of 1 or 2 = 1/6+1/6 as probability of 1 and 2 = 0
so the answer is 2/6=1/3
Need help plss answer

Answers
Answer:
x ≤ 1
Step-by-step explanation:
In the graph shown, the blue arrow is facing to the left, so we know that the inequality is some kind of less-than inequality (x < number).
We can also see that the blue arrow starts at a filled-in circle, so we know that the inequality will use the less-than-or-equal-to relator (≤).
Finally, the filled-in dot is at 1, so we can construct the equation:
x ≤ 1
Note that you could replace x with any other variable or even a blank space, since it isn't specified by the number line.
let t be a binary search tree with n nodes. when t is linear the search algorithm makes key comparisons in the unsuccessful case
Answers
Let T be a binary search tree with n nodes, in which n > 0. When I is linear, the search algorithm makes n key comparisons, in unsuccessful case.
The BST (Binary Search Tree) is a tree where all nodes on the left and right sides of a given node are larger and less than each other.
The nodes of the BST are not kept in a continuous location because it is a non-linear data structure. The element is absent from the list in the best-case scenario, making it a worst-case scenario.
The worst-case temporal complexity for linear structures is O. (n).
In the worst scenario, there will be n key comparisons.
To learn more about binary search tree link is here
brainly.com/question/12946457
#SPJ4
The right question is:
Let T be a binary search tree with n nodes, in which n > 0. When I is linear, the search algorithm makes.......................... key comparisons, in unsuccessful case.
aluate expressions
(5 + 3) •8-22
Answers
Answer:
42
Step-by-step explanation:
(5+3) x 8 -22
8 x 8 -22
64 - 22
42
Answer:
42
Step-by-step explanation:
You Use PEMDAS
I’m am so lost please help thank you all

Answers
Answer:
Step-by-step explanation:
148 people
it is due today, please help me. If you just want points get out of my question page...


Answers
To completely solve the problem, Karim should convert the product back into standard decimal notation.
We cannot directly apply the product of powers property because the binomial is not raised to a power itself.
Miscellaneous problem(1) To convert a number from scientific notation to standard decimal notation, we multiply the coefficient (0.0258) by 10 raised to the power of the exponent (-8).
0.0258 × \(10^{-8\) = 0.0258 × 0.00000001
= 0.000000000000258
(2) The product of powers property states that when you raise a term with an exponent to another exponent, you can simplify it by multiplying the exponents.
In the expression \((3z + y)^3\), we have a binomial term (3z + y) raised to the power of 3. This is not a situation where we can directly apply the product of powers property because the binomial is not raised to a power itself.
To simplify the expression, we need to expand it using the binomial theorem or by applying the concept of binomial expansion.
More on powers property can be found here: https://brainly.com/question/2499975
#SPJ1
What is the opposite of the opposite of -1.4?
Answers
Answer:
1.4
Step-by-step explanation:
when we add -1.4 and 1.4 we get zero so its the opposite
The base of a square pyramid was dilated with k=0.55. The area of the base is 1600 square units Find the area of the cross section.
Answers
The area of the cross section after the dilation has a value of 484 square units
Calculating the area of the cross section.
When a square pyramid is dilated, all of its dimensions, including the base area and height, are multiplied by the same factor.
In this case, the base of the pyramid was dilated with a factor of k=0.55.
Therefore, the new area of the base can be calculated as:
New base area = k^2 * old base area
Plugging in the values given in the problem, we get:
New base area = (0.55)^2 * 1600
New base area = 484 square units
So, the new base area is 484 square units
Read more about dilation at
https://brainly.com/question/3457976
#SPJ1
PLEASE HELP
Write the equation of the line that is perpendicular to the given segment and that passes through the point (-6, -3). A. 1 V=--x-3 2 B. 1 V=--X-6 2 C. y = 2x + 9 D. = 2x-6.

Answers
Answer:
C
Step-by-step explanation:
The slope of the line will be (2) and the equation will be C
I have to express in terms of logarithms but somehow i keep messing up. Could someone who knows logarithms help?

Answers
\(\begin{array}{llll} \textit{Logarithm of exponentials} \\\\ \log_a\left( x^b \right)\implies b\cdot \log_a(x) \end{array}~\hfill \begin{array}{llll} \textit{Logarithm Cancellation Rules} \\\\ \stackrel{\stackrel{\textit{we'll be using this one}}{\downarrow }~\hfill }{log_a a^x = x\qquad \qquad a^{log_a x}=x} \end{array}\)
\(\textit{Logarithm Change of Base Rule} \\\\ \log_a b\implies \cfrac{\log_c b}{\log_c a}\qquad \qquad c= \begin{array}{llll} \textit{common base for }\\ \textit{numerator and}\\ denominator \end{array} \\\\[-0.35em] \rule{34em}{0.25pt}\)
\(2^{0.5x}=10\implies \log_2\left( 2^{0.5x} \right)=\log_2(10)\implies 0.5x=\log_2(10) \\\\\\ \cfrac{x}{2}=\log_2(10)\implies x = 2\log_2(10)\implies x = \log_2(10^2)\implies x = \log_2(100) \\\\\\ \stackrel{\textit{using the change of base rule}}{x = \cfrac{\log(100)}{\log(2)}\implies x = \cfrac{2}{\log(2)}}\implies x\approx 6.644\)
as far as the domain, or namely what values "x" can take on safely, I don't see any constraints, so it must be (-∞ , +∞).
ITS THE FOURTH QUESTION

Answers
The surface areas of the figures are 336, 82 and 836
How to calculate the surface areasFrom the question, we have the following parameters that can be used in our computation:
The figures
For the triangular prism, we have
Surface area = 2 * 1/2 * 6 * 8 + 12 * 10 + 8 * 12 + 6 * 12
Surface area = 336
For the rectangular prism, we have
Surface area = 2 * (7 * 3 + 3 * 2 + 2 * 7)
Surface area = 82
For the cylinder, we have
Surface area = 2π * 7 * (7 + 12)
Surface area = 836
Read more about surface area at
https://brainly.com/question/76387
#SPJ1
The surface area of the prisms are
1. 336 cm²
2. 82 m²
3. 836 cm²
What is surface area?The area occupied by a three-dimensional object by its outer surface is called the surface area.
A prism is a solid shape that is bound on all its sides by plane faces.
The surface area of prism is expressed as;
SA = 2B +pH
where B is the base area , p is the perimeter and h is the height.
1. SA = 2B +ph
B = 1/2 × 6 × 8
= 24 m²
p = 6+8+10 = 24m
h = 12m
SA = 2 × 24 + 24 × 12
= 48 + 288
= 336 cm²
2. SA = 2( 3× 2) + 3× 7)+ 2 × 7)
= 2( 6+21+14)
= 2( 41)
= 82 m²
3. SA = 2πr( r +h)
= 2 × 3.14 × 7( 7 + 12)
= 44( 19)
= 836 cm²
learn more about surface area from
https://brainly.com/question/16519513
#SPJ1
The revenue of a company is represented by 3x² + 9x + 5 and the costs by 3x² + 3x + 21. If the profit can be found by subtracting cost from revenue, what expression could represent the profit? I
Answers
Subtract the cost equation from the revenue equation
The 3X^2 cancel each other out
9X-3X= 6X
And 5-21= -16
Leaving 6X-16
help me plzzzzzzzzzzz
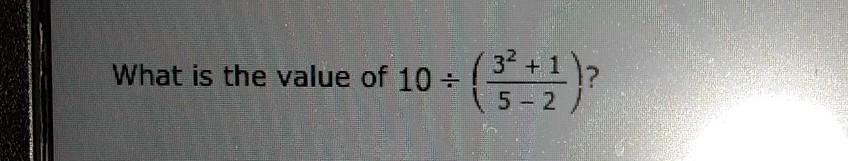
Answers
Answer:
\(3\)
Step-by-step explanation:
\(10 \div ( \frac{ {3}^{2} + 1 }{5 - 2} )\)
\( \frac{10(5 - 2)}{ {3}^{2} + 1} \)
\( \frac{10 \times 3}{ {3}^{2} + 1 } \)
\( \frac{30}{ {3}^{2} + 1 } \)
\( \frac{30}{9 + 1} \)
\( \frac{30}{10} \)
\(3\)
five times a number minus two is ten .find the number
Answers
Answer:
12/5 or 2.4
Step-by-step explanation:
Form the equation:
5x - 2 = 10
^ ^ ^
^ ^ "is ten" which adds a equal sign to it
^ minus two
five times a number
Solve:
5x - 2 = 10
+2 +2
-----------------
5x = 12
---- ----
5 5
x = 12/5 or 2.4
Let the number be x
Then ATQ
5x - 2 = 10
5x = 10+2
x = 12/5
Must click thanks and mark brainliest
Which ratio is less than
7/15
o
Answers
The length of a rectangle is twice its width. Find its lenght and width, if its perimeter is 7 1/3 cm.
Answers
The length of the rectangle is twice its width. If its perimeter is 7 1/3 cm, its length will be 22/9 cm, and the width is 11/9 cm.
Let's assume the width of the rectangle is "b" cm.
According to the given information, the length of the rectangle is twice its width, so the length would be "2b" cm.
The formula for the perimeter of a rectangle is given by:
Perimeter = 2 * (length + width)
Substituting the given perimeter value, we have:
7 1/3 cm = 2 * (2b + b)
To simplify the calculation, let's convert 7 1/3 to an improper fraction:
7 1/3 = (3*7 + 1)/3 = 22/3
Rewriting the equation:
22/3 = 2 * (3b)
Simplifying further:
22/3 = 6b
To solve for "b," we can divide both sides by 6:
b = (22/3) / 6 = 22/18 = 11/9 cm
Therefore, the width of the rectangle is 11/9 cm.
To find the length, we can substitute the width back into the equation:
Length = 2b = 2 * (11/9) = 22/9 cm
So, the length of the rectangle is 22/9 cm, and the width is 11/9 cm.
For more information on the Perimeter of the Rectangle, click:
https://brainly.com/question/13757874
please someone help me with maths

Answers
Answer:
a)= 5x+10
b)= 7y-6
c)= 6x-6
d)= 2x^2+8x-5
e)= 6x+9
f)= 4xy-4y^2+8y
g)= -12y^2+10y
h)= 6x+154
i)= 6x+21
h)= 2x^2+16
