Answers
Answer:
answer is 5 hope this helps

Answer:
5
Step-by-step explanation:
Related Questions
Is the relation shown in the table below a function? (type in yes or no)

Answers
Answer:
Yes
Step-by-step explanation:
To know if a table is a function or not, we have to see if 1 input only has 1 output.
Looking at the table each input only has 1 output, so it is a function.
The number of typos made by a student follows Poisson distribution with the rate of 1.5 typos per page. Assume that the numbers of typos on different pages are independent. (a) Find the probability that there are at most 2 typos on a page. (b) Find the probability that there are exactly 10 typos in a 5-page paper. (c) Find the probability that there are exactly 2 typos on each page in a 5-page paper. (d) Find the probability that there is at least one page with no typos in a 5-page paper. (e) Find the probability that there are exactly two pages with no typos in a 5-page paper.
Answers
Answer:
a) 0.8088 = 80.88% probability that there are at most 2 typos on a page.
b) 0.0858 = 8.58% probability that there are exactly 10 typos in a 5-page paper.
c) 0.001 = 0.1% probability that there are exactly 2 typos on each page in a 5-page paper.
d) 0.717 = 71.7% probability that there is at least one page with no typos in a 5-page paper.
e) 0.2334 = 23.34% probability that there are exactly two pages with no typos in a 5-page paper.
Step-by-step explanation:
Poisson distribution:
In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:
\(P(X = x) = \frac{e^{-\mu}*\mu^{x}}{(x)!}\)
In which
x is the number of sucesses
e = 2.71828 is the Euler number
\(\mu\) is the mean in the given interval.
Binomial distribution:
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
In which \(C_{n,x}\) is the number of different combinations of x objects from a set of n elements, given by the following formula.
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
And p is the probability of X happening.
The number of typos made by a student follows Poisson distribution with the rate of 1.5 typos per page.
This means that \(\mu = 1.5n\), in which n is the number of pages.
(a) Find the probability that there are at most 2 typos on a page.
One page, which means that \(\mu = 1.5\)
This is
\(P(X \leq 2) = P(X = 0) + P(X = 1) + P(X = 2)\)
In which
\(P(X = x) = \frac{e^{-\mu}*\mu^{x}}{(x)!}\)
\(P(X = 0) = \frac{e^{-1.5}*(1.5)^{0}}{(0)!} = 0.2231\)
\(P(X = 1) = \frac{e^{-1.5}*(1.5)^{1}}{(1)!} = 0.3347\)
\(P(X = 2) = \frac{e^{-1.5}*(1.5)^{2}}{(2)!} = 0.2510\)
\(P(X \leq 2) = P(X = 0) + P(X = 1) + P(X = 2) = 0.2231 + 0.3347 + 0.2510 = 0.8088\)
0.8088 = 80.88% probability that there are at most 2 typos on a page.
(b) Find the probability that there are exactly 10 typos in a 5-page paper.
5 pages, which means that \(n = 5, \mu = 5(1.5) = 7.5\).
This is P(X = 10). So
\(P(X = x) = \frac{e^{-\mu}*\mu^{x}}{(x)!}\)
\(P(X = 10) = \frac{e^{-7.5}*(7.5)^{10}}{(10)!} = 0.0858\)
0.0858 = 8.58% probability that there are exactly 10 typos in a 5-page paper.
(c) Find the probability that there are exactly 2 typos on each page in a 5-page paper.
Two typos on a page: 0.2510 probability.
Two typos on each of the 5 pages: (0.251)^5 = 0.001
0.001 = 0.1% probability that there are exactly 2 typos on each page in a 5-page paper.
(d) Find the probability that there is at least one page with no typos in a 5-page paper.
0.2231 probability that a page has no typo, so 1 - 0.2231 = 0.7769 probability that there is at least one typo in a page.
(0.7769)^5 = 0.283 probability that every page has at least one typo.
1 - 0.283 = 0.717 probability that there is at least one page with no typos in a 5-page paper.
(e) Find the probability that there are exactly two pages with no typos in a 5-page paper.
Here, we use the binomial distribution.
0.2231 probability that a page has no typo, so \(p = 0.02231\)
5 pages, so \(n = 5\)
We want P(X = 2). So
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(P(X = 2) = C_{5,2}.(0.2231)^{2}.(0.7769)^{3} = 0.2334\)
0.2334 = 23.34% probability that there are exactly two pages with no typos in a 5-page paper.
I grew up on a pig farm. We raised baby pink pigs from birth to 8 weeks old. A 90% confidence interval is calculated for a sample of weights of 135 randomly selected 8-week old pigs. The resulting confidence interval is 75 to 90 pounds. Will the sample mean weight, from this random sample of 135 pigs, fall within the confidence interval?
a. yes
b. no
c. maybe
Answers
Answer:
A
Step-by-step explanation:
3 4 5 6
The sample mean weight, from this random sample of 135 pigs, fall within the confidence interval. (Option A: yes)
How to find the confidence interval for large samples (sample size > 30)?Suppose that we have:
Sample size n > 30Sample mean = \(\overline{x}\)Sample standard deviation = \(s\)Population standard deviation = \(\sigma\)Level of significance = \(\alpha\)Then the confidence interval is obtained as
Case 1: Population standard deviation is known\(\overline{x} \pm Z_{\alpha /2}\dfrac{\sigma}{\sqrt{n}}\)
Case 2: Population standard deviation is unknown.\(\overline{x} \pm Z_{\alpha /2}\dfrac{s}{\sqrt{n}}\)
For this case, we work with sample standard deviation(you can choose even population standard deviation, it won't matter as both are not given here).
We're provided that:
Sample size = n = 135Confidence interval is of 90%, therefore, Level of significance = \(\alpha\) = 100 - 90% = 10% = 10/100 = 0.1 (converted percent to decimal)The critical value of Z at 0.1 level of significance is \(\pm 1.645\)Confidence interval's limits = 75 (lower limit) and 90(upper limit) (in pounds)Sample mean = \(\overline{x}\)Sample standard deviation = \(s\)Since the formula for limits of confidence interval is:
\(\overline{x} \pm Z_{\alpha /2}\dfrac{s}{\sqrt{n}} = \overline{x} \pm 1.645\dfrac{s}{\sqrt{135}}\)
That has:
\(\text{Lower limit} = 75 = \overline{x} - 1.645\dfrac{s}{\sqrt{135}}\\\\\text{Upper limit} = 90 = \overline{x} +1.645\dfrac{s}{\sqrt{135}}\\\\\)
Thus, we get:
Adding both the equations, we get:
\(165 = 2\overline{x}\\\\\overline{x} = 82.5 \: \rm pounds\)
That is between 75 and 90 pounds.
Thus, the sample mean weight, from this random sample of 135 pigs, fall within the confidence interval. (Option A: yes)
Learn more about confidence interval for large samples here:
https://brainly.com/question/13770164
I need help with this problem

Answers
at x = 1 we have one tangent line and at x = 5 we have just another tangent line.
\(f(x)=3x^2-15x\implies \left. \cfrac{df}{dx}=6x-15 \right|_{x=1}\implies \stackrel{\stackrel{m}{\downarrow }}{-9}~\hfill \left. 6x-15\cfrac{}{} \right|_{x=5}\implies \stackrel{\stackrel{m}{\downarrow }}{15}\)
so we have the slopes, but what about the coordinates?
well, for the first one we know x = 1 and we also know f(x), let's use f(1) to get "y", and likewise we'll do the for the second one.
\(\stackrel{x=1}{f(1)}=3(1)^2-15(1)\implies f(1)=-12\qquad \qquad (\stackrel{x_1}{1}~~,~~\stackrel{y_1}{-12}) \\\\\\ \begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-12)}=\stackrel{m}{-9}(x-\stackrel{x_1}{1}) \\\\\\ y+12=-9x+9\implies y=-9x-3 \\\\[-0.35em] ~\dotfill\)
\(\stackrel{x=5}{f(5)}=3(5)^2-15(5)\implies f(5)=0\qquad (\stackrel{x_1}{5}~~,~~\stackrel{y_1}{0}) \\\\\\ \begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{0}=\stackrel{m}{15}(x-\stackrel{x_1}{5})\implies y=15x-75\)
The midpoint of AB ‾ AB is M ( − 1 , − 5 ) M(−1,−5). If the coordinates of A are ( 3 , − 8 ) (3,−8), what are the coordinates of B?
Answers
Answer:
(-5,-2)
Step-by-step explanation:
To find the mid-point the formula is;
\((x_1+x_2)/2 ,(y_1+y_2)/2\)
In this case point A (3,-8) , mid-point (-1,-5), point B (x,y)
Thus (3+x)/2 = -1
3+x=-2
x= -2-3 = -5
And
( -8+y)/2 = -5
-8 + y = -5*2
-8 +y = -10
y= -10 +8 = -2
Hence point B coordinates are: (-5, -2)
The slopes of perpendicular lines are negative reciprocals.TrueFalse
Answers
Answer:
True
Step-by-step explanation:
Given that 8 tan = 3 cos
a) Show that the above equation can be rewritten in the form 3 sin2 + 8 sin − 3 = 0
b) Hence solve, for 0 ≤ ≤ 90, the equation 8 tan 2 = 3 cos 2, giving your answers to 2 decimal places.
Answers
The only solution for the equation 8 tan^2 θ = 3 cos^2 θ in the given Range is θ ≈ 19.47 degrees.
a) We are given the equation 8 tan θ = 3 cos θ.
Dividing both sides of the equation by cos θ, we have:
8 tan θ / cos θ = 3
Using the identity tan θ = sin θ / cos θ, we can substitute it into the equation:
8 (sin θ / cos θ) / cos θ = 3
Simplifying further, we get:
8 sin θ / cos^2 θ = 3
Now, multiplying both sides of the equation by cos^2 θ, we have:
8 sin θ = 3 cos^2 θ
Using the identity cos^2 θ = 1 - sin^2 θ, we can substitute it into the equation:
8 sin θ = 3(1 - sin^2 θ)
Expanding the equation, we get:
8 sin θ = 3 - 3 sin^2 θ
Rearranging the terms, we have:
3 sin^2 θ + 8 sin θ - 3 = 0
Therefore, we have successfully shown that the equation can be rewritten in the form 3 sin^2 θ + 8 sin θ - 3 = 0.
b) Now, let's solve the equation 3 sin^2 θ + 8 sin θ - 3 = 0.
To solve the quadratic equation, we can use factoring, quadratic formula, or other appropriate methods.
In this case, the equation factors as:
(3 sin θ - 1)(sin θ + 3) = 0
Setting each factor equal to zero, we have two equations:
3 sin θ - 1 = 0 or sin θ + 3 = 0
For the first equation, solving for sin θ, we get:
3 sin θ = 1
sin θ = 1/3
Taking the inverse sine (sin^-1) of both sides, we find:
θ = sin^-1(1/3) ≈ 19.47 degrees (to 2 decimal places)
For the second equation, solving for sin θ, we have:
sin θ = -3
Since the range of sine is between -1 and 1, there are no solutions for this equation in the given range (0 ≤ θ ≤ 90 degrees).
Therefore, the only solution for the equation 8 tan^2 θ = 3 cos^2 θ in the given range is θ ≈ 19.47 degrees.
To know more about Range .
https://brainly.com/question/30389189
#SPJ11
Robert's book bag is weighing him down. His bag alone weighs 4 pounds. His library book
weighs 2 pounds. The math book is 4 times the weight of the library book, and his science
book is 2 times the weight of the math book. How much does his book bag weigh with all
these books? What is the heaviest book in his book bag?
Answers
The library book weighs 2 pounds.
The math book is 4 times the weight of the library book, so it weighs 4 * 2 = 8 pounds.
The science book is 2 times the weight of the math book, so it weighs 2 * 8 = 16 pounds.
To find the total weight of Robert's book bag, we add the weights of all the books and the bag:
4 pounds (bag) + 2 pounds (library book) + 8 pounds (math book) + 16 pounds (science book) = 30 pounds.
Therefore, Robert's book bag weighs 30 pounds with all these books.
To determine the heaviest book in his book bag, we compare the weights of the books:
The bag weighs 4 pounds.
The library book weighs 2 pounds.
The math book weighs 8 pounds.
The science book weighs 16 pounds.
From these options, the science book is the heaviest, weighing 16 pounds.
Answer:
1) 30 pounds is the weight of the bag all together
2) science book is the heaviest book
Step-by-step explanation:
bag=4 pounds
library book=2 pounds
maths book=2×4=8 pounds
science book=8×2=16 pounds
4+2+8+16=30 pounds all together
heaviest book= science book (16 pounds)
Given f(x)= x^2-3x+4, find f(x+2)-f(2).
Answers
Is that what you want

Answer:
f ( x+2) – f(2) = x² + x
Step-by-step explanation:
f(x) = x² – 3x+4
f(x+2) = (x+2)² – 3 (x+2) +4
= ( x²+ 4x + 4) – 3x – 6 +4
= x² + 4x +4 – 3x – 6 + 4
= x² + x +2
f(x) = x² – 3x+4
f(2) = 2² – 3(2) +4 = 4 – 6 + 4 = 2
f ( x+2) – f(2) = (x² +x +2 ) – (2)
= x² + x +2 – 2
= x² + x
I hope I helped you^_^
The vertices of triangle ABC are given: A (0;-1) B(12; -10) C(10;4)
Find:
a) the equation of the median and bisector drawn from vertex A;
b) the equation of the altitude from vertex B;
c) the point of intersection of the median and height;
d) the coordinates of the center of mass (the point of intersection of the medians).
Answers
verified
Verified by Toppr
Median bisects the line.
D≡(
2
−3+5
,
2
−9−8
)≡(1,
2
−17
)
E≡(−
2
1+5
,
2
6−8
)≡(2,−1)
F≡(−
2
1−3
,
2
6−9
)≡(−2,
2
−3
)
∴ equation of AD:(y−y
1
)=(
x
2
−x
1
y
2
−y
1
)
AD
(x−x
1
)
⇒(y−6)=
⎝
⎜
⎜
⎛
1+1
2
−17
−6
⎠
⎟
⎟
⎞
(x+1)⇒(y−6)=−
4
29
(x+1)
⇒
4
29
x+y−6+
4
29
=0
AD⇒29x+4y+5=0
equation of BE:(y+9)=(−
2+3
1+9
)
BE
(x+3)
⇒(y+9)=
5
8
(x+3)⇒5y+45=8x+24
BE⇒8x−5y−21=0
Equation of CF:(y+8)=
⎝
⎜
⎜
⎛
−2−5
−
2
3
+8
⎠
⎟
⎟
⎞
CF
(x−5)
⇒(y+8)=−
14
13
(x−5)⇒14y+112=−13x+65
CF:13x+14y+47=0
Find the slope of the lined graph

Answers
The slope of the lined graph is 5 / 3
How to determine the slope
The formula for determining the slope of a line is expressed as;
Slope = y2 - y1/ x2 - x1
From the graph shown;
y1 = -1y2 = 4x2 = 3x1 = 0Now, let's substitute the values
Slope, m = 4 - (-1) / 3 - 0
Find the differences
Slope, m = 4 + 1/ 3
Slope, m = 5 / 3
Thus, the slope of the lined graph is 5 / 3
Learn more about slope here:
https://brainly.com/question/3493733
#SPJ1
Naty bought a dress for $24.95 and a skirt for $14.95. The sales clerk said the total cost including 9.5% sales tax was $49.40. Below are the steps the sales clerk completed.
Step 1: 24.95 + 14.95 = 39.90
Step 2: 39.90 + 9.5 = 49.40
Are the clerk's steps correct? If she is incorrect, identify her mistake and explain her error. Explain in writing how to accurately calculate the sales tax, the total cost, and state the correct total. (Round the final answer to the nearest hundredth)
Answers
She is incorrect. The mistake she made was adding $9.5 instead of taking 9.5% from the $39.90 and adding it to the initial total. The correct answer is actually $43.69. To find sales tax add your two starting prices and simply find the percent your looking for and add it to the original total
Answer:
see below
Step-by-step explanation:
Clerk is wrong at step two. It should be...
To calculate the sales tax take 9.5% and divide by 100 which is 0.095. The tax is 0.095(39.90) = 3.79
Cost of items + Tax = Total cost
Cost of items + .095(cost of items) = Total cost
39.90 + 3.79 = 43.69
Which of the following statements is not true?
Choose the incorrect statement below.
The three-part inequality - 1 <-3x ≤ 1 is equivalent to -5x<
15x2
<3 is equivalent to -6≤5-x<6.
The three-part inequality - 3s-
OD. The three-part inequality -7≤11-x<7 is equivalent to 4 < x≤ 18.
OA.
OB.
C.
The three-part inequality -5s-10x<5 is equivalent to
5-x
...
Answers
The incorrect statement is:
B. The three-part inequality - 5x < 15x^2 < 3 is equivalent to - 6 ≤ 5 - x < 6.
In the given statement, there is an error in the inequality. The correct statement should be:
The three-part inequality - 5x < 15x^2 < 3 is equivalent to - 6 ≤ 5 - x and 5 - x < 6.
When solving the three-part inequality - 5x < 15x^2 < 3, we need to split it into two separate inequalities. The correct splitting should be:
- 5x < 15x^2 and 15x^2 < 3
Simplifying the first inequality:
- 5x < 15x^2
Dividing by x (assuming x ≠ 0), we need to reverse the inequality sign:
- 5 < 15x
Simplifying the second inequality:
15x^2 < 3
Dividing by 15, we get:
x^2 < 1/5
Taking the square root (assuming x ≥ 0), we have two cases:
x < 1/√5 and -x < 1/√5
Combining these inequalities, we get:
- 5 < 15x and x < 1/√5 and -x < 1/√5
Therefore, the correct statement is that the three-part inequality - 5x < 15x^2 < 3 is equivalent to - 6 ≤ 5 - x and 5 - x < 6, not - 6 ≤ 5 - x < 6 as stated in option B.
For more such questions on inequality
https://brainly.com/question/30681777
#SPJ8
Will mark BRAINLIEST!! This is pt.2

Answers
Answer:
See below.
Step-by-step explanation:
Problem 3.
1. <3, <4
Given
2. <1, <2
Given
3. KG
Congruence of segments is reflexive.
4. HKG, LKG
ASA
Problem 4.
1. MR, OR
Given
2. PR, NR
Given
3. <2
Vertical angles are congruent.
4. MPR, ONR
SAS
-2 (8p+2) -3(2-7p)=2(4+2p)
Answers
Answer:
p = 18
Step-by-step explanation:
Let's solve your equation step-by-step.
−2(8p+2)−3(2−7p)=2(4+2p)
Step 1: Simplify both sides of the equation.
−2(8p+2)−3(2−7p)=2(4+2p)
(−2)(8p)+(−2)(2)+(−3)(2)+(−3)(−7p)=(2)(4)+(2)(2p)(Distribute)
−16p+−4+−6+21p=8+4p
(−16p+21p)+(−4+−6)=4p+8(Combine Like Terms)
5p+−10=4p+8
5p−10=4p+8
Step 2: Subtract 4p from both sides.
5p−10−4p=4p+8−4p
p−10=8
Step 3: Add 10 to both sides.
p−10+10=8+10
p=18
Therefore, the final answer is 18, I hope this helps :D
Answer:
p=18
Step-by-step explanation:
See image below:)

the question is below

Answers
Answer:
sin I = \(\frac{80}{89}\)
Step-by-step explanation:
sin I = \(\frac{opposite}{hypotenuse}\) = \(\frac{KJ}{JI}\) = \(\frac{80}{89}\)
18 ABCDEFGH is a cuboid. AB= 7.3 cm CH= 8.1 cm Angle BCA = 48° F A E D G B Find the size of the angle between AH and the plane ABCD Give your answer correct to 1 decimal place. H C (Total for Question 18 is 4 marks)
Answers
The size of the angle between AH and the plane ABCD is approximately 74.4°, rounded to one decimal place.
To find the size of the angle between AH and the plane ABCD in the given cuboid, we can use the concept of three-dimensional geometry.
First, let's consider the right triangle BCA. The given angle BCA is 48°, and we know that the length of AB is 7.3 cm. Using trigonometric functions, we can find the length of BC:
BC = AB * sin(BCA)
BC = 7.3 * sin(48°)
BC ≈ 5.429 cm
Now, let's look at the right triangle BAH. The length of AH is given as 8.1 cm. We can find the length of BH by subtracting BC from AB:
BH = AB - BC
BH ≈ 7.3 - 5.429
BH ≈ 1.871 cm
Next, let's consider the right triangle ABH. We want to find the angle BAH, which is the complement of the angle between AH and the plane ABCD. We can use the cosine function to find the angle BAH:
cos(BAH) = BH / AH
cos(BAH) ≈ 1.871 / 8.1
BAH ≈ arccos(1.871 / 8.1)
BAH ≈ 74.4°
For more such questions on angle
https://brainly.com/question/31615777
#SPJ8
cuanto es la respuesta de 579 x 784
Answers
Answer:
453936
que tenga un lindo día
Answer:
453936
Step-by-step explanation:
Hope this helps!
Graph the system of equations on your graph paper to answer the question.
{y=x−4y=−x+6
What is the solution for this system of equations?
Answers
Answer: (5 , 1)
Step-by-Step explanation:
hihi your problem is a system of question y = x-4 and y = -x+6 okay so graph them both normally and then find the point where they intersect which is gonna be a coordinate point, and that's your solution !!
y = x-4
the y intersect is going to be 4
the slope is a positive 1 , going up to the right, through the positive quadrant, line is facing to the right
y = -x+6
the y intersect is going to be -6
the slope is going to be a -1 , following up the opposite way the line is going to face the left
once you graph them both you'll see the point of intersection, the solution
make sure you drew your lines very clearly !!!!
the solution is x = 5 and y = 1 which is also (5 , 1)
hopefully this was helpful !
Calculate 3cm ,4cm, 10cm and 2cm
Answers
Answer:
19cm
Step-by-step explanation:
(chose one way)
1. way using commutativity
(3cm+4cm)+(10cm+2cm)=7cm+12cm=19cm
2. way just writing
3cm+4cm+10cm+2cm=19cm
What is the x-value in the solution to this system of linear equations?
2x - y = 11
x + 3y = -5
0-3
0 -1
O 2
O4
PLEASE HELP :)
Answers
Solving Steps:
2x-y=11
x+3y=-5
-2x-y=11
-2x-6y=10
-7y=21
y=-3
x+3(-3)=-5
x=4
A circular garden has a circumference of 63 yards. Lars Is digging a straight line along a diameter of the garden at a rate of 5 yards per hour. How many hours will it take him to dig across the garden? Use 3.14 for 1 and round the diameter to the nearest whole number, if necessary. It will take Lars about hours to dig across the garden.
PLZ answer need by 10:40
Answers
Answer:
4 hours
Step-by-step explanation:
f the circumference of the circular garden =63 yards
Circumference of a Circle =2πr=πd (d=diameter)
Therefore:
πd= 63
diameter of the circular garden =63/3.14=20 yards
If he digs at a rate of 5 yards per hour, the time required to dig across the garden will be:
20 yards/5 yard per hours = 4 hours
It will take him 4 hours to dig across the circular garden.
Easy math questions, I just don't have time, ASAP PLEASE
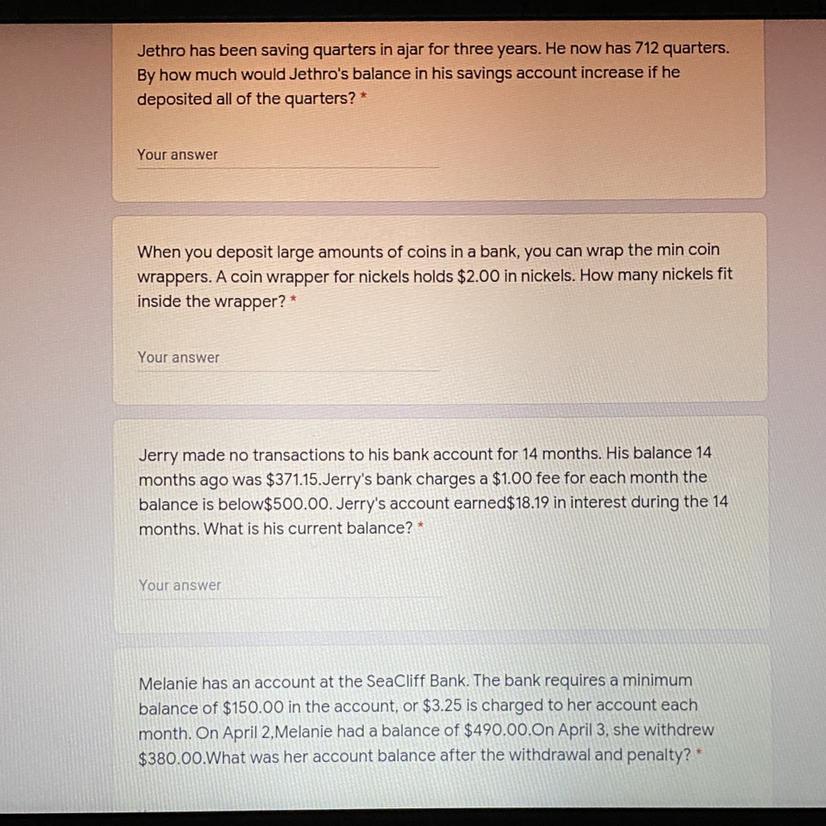
Answers
The second one would be 8 quarters
His current balance is $321.34
She would have $110.00 but with penalty she would have $106.75
You are choosing between two health clubs club a offers membership for a fee of $13 plus a monthly fee of $28 club B offers membership for a fee of $19 plus a monthly fee of $27 after how many months will the total cost of each health club be the same? What will be the total cost for each club?
Answers
To determine when the total cost of each health club will be the same, we can set up an equation and solve for the number of months.
Let's assume the number of months is represented by 'x'.
For Club A, the total cost is given by:
Total cost of Club A = $13 (one-time fee) + $28x (monthly fee)
For Club B, the total cost is given by:
Total cost of Club B = $19 (one-time fee) + $27x (monthly fee)
To find the number of months when the total cost is the same, we set the two equations equal to each other:
$13 + $28x = $19 + $27x
Simplifying the equation, we get:
$28x - $27x = $19 - $13
$x = 6
Therefore, after 6 months, the total cost of each health club will be the same.
To find the total cost for each club after 6 months, we substitute the value of 'x' back into the equations:
Total cost of Club A after 6 months = $13 + $28(6) = $13 + $168 = $181
Total cost of Club B after 6 months = $19 + $27(6) = $19 + $162 = $181
So, the total cost for both Club A and Club B will be $181 after 6 months.
For such more question on equation
https://brainly.com/question/29174899
#SPJ8
Please explain how to combine them into one standard form equation.

Answers
9514 1404 393
Answer:
e. 7x -y = -5
Step-by-step explanation:
Rearranging the first equation to general form, we have ...
7x -2 = 0 . . . . subtract 5 from both sides
Rearranging the second equation to general form, we have ...
y -7 = 0 . . . . . subtract 6 from both sides
Now, we can equate these expressions for 0:
7x -2 = y -7
Subtracting y gives ...
7x -y -2 = -7
and adding 2 gives the standard form equation ...
7x -y = -5 . . . . matches choice E
_____
Comment on the question
Mathematically, there is no good reason to do this. It seems to be simply an exercise in manipulating equations.
Here, we subtracted the y-equation from the x-equation to get the final result. There are many other ways an expression for "0" can be used to combine these equations.
Tram Fancy Balloons has offered to sell its balloon bouquet for a fixed down payment of $30 and an additional charge of $3 25 per bouquet
Write an algebraic rule that will determine the cost of "c" balloon bouquets
Answers
Answer:
y = 30 + 3.25c
(where y is the total cost in dollars, and c is the number of balloon bouquets)
Step-by-step explanation:
Let y = total cost (in dollars)
Let c = number of balloon bouquets
Given:
Fixed payment = $30Charge per bouquet = $3.25⇒ y = 30 + 3.25c
Y inetercept:-
Fixed payment=30Rate of change=3.25
So
No of balloons=cCost be Y
Y=3.25c+3022 Find the circumference of the circle, Use 3.14 or for x. Round to the nearest tenth if necessary, 31.5 cm

Answers
ANSWER:
The circumference is 198 cm
STEP-BY-STEP EXPLANATION:
We have the formula to calculate the circumference of the circle is the following:
\(c=2\pi r\)we replace the value of pi and the radius:
\(\begin{gathered} c=2\cdot\frac{22}{7}\cdot31.5 \\ c=198 \end{gathered}\)how to get the area of the base ?
Answers
Answer:
LxWxH
Step-by-step explanation:
Bases
The area of a rectangle is equal to its length, l, multiplied by its width, w: A = l x w.
example: Given a pyramid whose base is 10 inches long and 15 inches wide, find area as follows: A = 10 inches x 15 inches = 150 square inches.
Westside Energy charges its electric customers a base rate of $8.00 per month, plus 12¢ per kilowatt-hour (kWh) for the first 300 kWh used and 4¢ per kWh for all usage over 300 kWh. Suppose a customer uses x kWh of electricity in one month. Express the monthly cost E as a piecewise defined function of x. (Assume E is measured in dollars.)

Answers
The linear function that gives the monthly cost E for x > 300 is given by:
E(x) = 44 + 0.04x.
What is a linear function?A linear function is modeled by:
y = mx + b
In which:
m is the slope, which is the rate of change, that is, by how much y changes when x changes by 1.b is the y-intercept, which is the value of y when x = 0, and can also be interpreted as the initial value of the function.When x > 300, we have that:
The base rate of $8.00 was paid.The 12 cents for each kWh up to 300 was paid.Hence the intercept is given by:
b = 8 + 0.12 x 300 = 44.
The slope is the cost per kWh of 4 cents, hence the function is:
E(x) = 44 + 0.04x.
More can be learned about linear functions at https://brainly.com/question/24808124
#SPJ1
7 11/6 x 6 2/5
Please solve
