If f(x) = 3x + 7, find:
f(3) = [?]
Answers
Answer:
16
Step-by-step explanation:
f(3) = 3(3) + 7
f(3) = 9 + 7
f(3) = 16
Related Questions
ΔQRS is an isosceles triangle. What is the length of RT¯¯¯¯¯
R
T
? Round to the nearest hundredth. Enter your answer in the box.

Answers
\(\begin{array}{llll} \textit{using the pythagorean theorem} \\\\ a^2+o^2=c^2\implies o=\sqrt{c^2 - a^2} \end{array} \qquad \begin{cases} c=\stackrel{hypotenuse}{11}\\ a=\stackrel{adjacent}{6}\\ o=\stackrel{opposite}{RT} \end{cases} \\\\\\ RT=\sqrt{ 11^2 - 6^2}\implies RT=\sqrt{ 121 - 36 } \implies RT=\sqrt{ 85 }\implies RT\approx 9.22\)
factorize 20(x - y)^2- 45y^2
Answers
Answer:
\(20(x - y)² - 45y² = 5(2(x - y) + 3y)(2(x - y) - 3y)\)
Step-by-step explanation:
We can start by factoring out the common factor of 5 from both terms:
\(20(x - y)² - 45y² = 5(4(x - y)² - 9y²)\)
Now, we can see that we have a difference of squares in the second set of parentheses:
\(= 5(2(x - y) + 3y)(2(x - y) - 3y)\)
Therefore, the fully factorized expression is:
\(20(x - y)² - 45y² = 5(2(x - y) + 3y)(2(x - y) - 3y)\)
What is the probability that either event will occur?
25
A
5
B
15
5
P(A or B)=P(A) + P(B) - P(A and B)
P(A or B) = [?]
Enter as a decimal rounded to the nearest hundredth.
Enter
Answers
If the events A and B are mutually exclusive, meaning they cannot occur simultaneously, then the probability of both events occurring together is zero. In this case, the formula simplifies to P(A or B) = P(A) + P(B).
The probability that either event A or event B will occur can be calculated using the addition rule of probability. According to this rule, the probability of either event A or event B occurring is equal to the sum of the individual probabilities of each event minus the probability of both events occurring together.
In other words, P(A or B) = P(A) + P(B) - P(A and B)
However, if the events A and B are not mutually exclusive, then the probability of both events occurring together needs to be subtracted from the sum of their individual probabilities to avoid double-counting.
So, the final answer to the question "What is the probability that either event will occur?" depends on the specific probabilities of events A and B and whether they are mutually exclusive or not.
To learn more about : probability
https://brainly.com/question/13604758
#SPJ11
Guys what is the answer
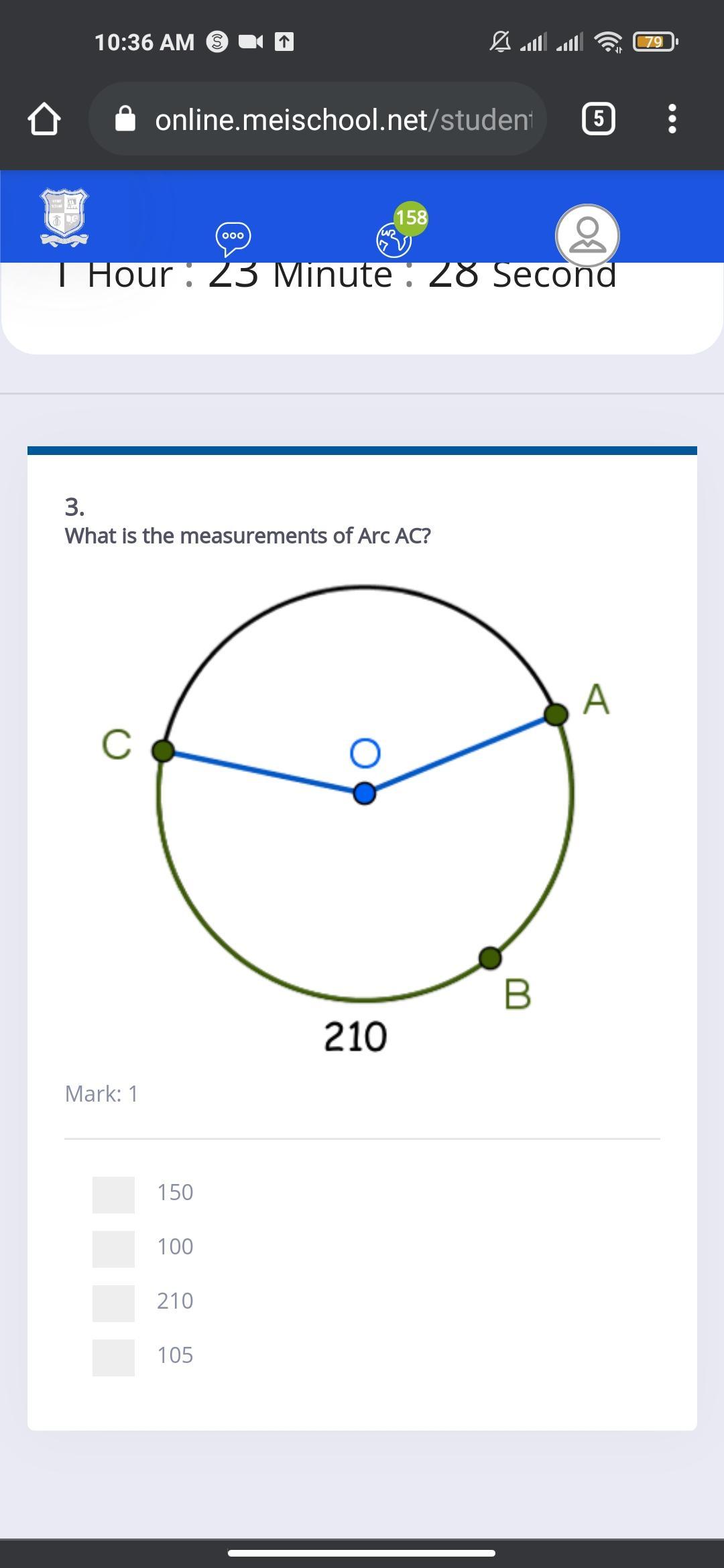
Answers
150°
Step-by-step explanation:
360° - 210° = 150° .......
If 343 is the third proportional of A and B, where a:b= 1:7 then the value of a+b will be
Answers
g/5 - 3 > 37. Solve for g. PLEASE HELPPP TYSM
Answers
Answer:
g = 200
Step-by-step explanation:
trust me.
I big brain.
What is the answer pleaseee

Answers
Answer: 803.84cm3
Step-by-step explanation:
The formula for finding the volume of a cylinder is πr2h.
In other words, the area of the top face's circle times the height.
To find the circle's area, we first find the radius of the circle. Since the diameter is 8cm, we divide by 2 to get the radius, which is 4cm.
4cm squared is 4cm x 4cm, which is 16cm. 16cm times 3.14 is 50.24cm squared.
Now, we have the area of the circle. 50.24cm squared!
The height is 16cm, so to find the cylinder, we times the area of the circle by the height of the cylinder! So,
16cm x 50.24cm squared = 803.84cm cubed.
The volume of the can of soup is 803.84cm cubed.
Please helpppp!!!!!
Algebra 2

Answers
Answer:
1209067.550.625Step-by-step explanation:
25% = 25/100 = 0.25
Then:
Bounce 1:
160 - (160*0.25) = 160 - 40 = 120
Bounce 2:
120 - (120*0.25) = 120 - 30 = 90
Bounce 3:
90 - (90*0.25) = 90 - 22.5 = 67.5
Bounce 4:
67.5 - (67.5*0.25) = 67.5 - 16.875 = 50.625
Find the perimeter and the area of each shape. Give your answer as a completely simplified exact value in terms of π (no approximations).

Answers
Answer:
Circumference: 12π + 8 cm,
Area: 48 ( cm )^2
Step-by-step explanation:
This figure is composed of circles, squares, and semicircles. As you can see, the squares indicate that each semicircle should have ( 1 ) the same area, and ( 2 ) the same length ( circumference ). It would be easier to take the circumference of the figure first, as it is composed of arcs part of semicircles the same length.
Circumference of 1 semicircle = \(\frac{1}{2}\)( πd ) = \(\frac{1}{2}\)π( 4 ) = 2π ( cm )
Circumference of Figure (composed of 6 semicircles + 2 sides of a square),
We know that 6 semicircles should be 6 \(*\) 2π, and as the sides of a square are equal - if one side is 4 cm, the other 3 are 4 cm as well. Therefore the " 2 sides of a square " should be 2
Circumference of Figure = 6 \(*\) 2π + 2 = 12π + 8 ( cm )
_____________
The area of this figure is our next target. As you can see, it is composed of 3 semicircles, and the area of 3 semicircles subtracted from the area of 3 squares. Therefore, let us calculate the area of 1 semicircle, and the area of 1 square first.
Area of 1 semicircle = 1/2π\(r^2\) = 1/2π\((2)^2\) = 2π ( cm ),
Area of 1 square = ( 4 cm )( 4 cm ) = 16 ( \(cm^2\) )
So, the area of the figure should be the following -
Area of Figure = 3 \(*\) 2π + 3( 16 - 2π ) = 48 ( cm )^2
Invent examples of data with
(a) SS(between) = 0 and SS(within) > 0
(b) SS(between) > 0 and SS(within) = 0
For each example, use three samples, each of size 5.
Answers
The sample of given data is Sample 1: 1, 2, 3, 4, 5 Sample 2: 6, 7, 8, 9, 10
b)Sample 1: 1, 2, 3, 4, 5 Sample 2: 6, 7, 8, 9, 10
(a) An example of data with SS(between) = 0 and SS(within) > 0 could be the following:
Sample 1: 1, 2, 3, 4, 5
Sample 2: 6, 7, 8, 9, 10
Sample 3: 11, 12, 13, 14, 15
In this example, the means of each sample are all different from each other, but the grand mean (8) is equal to the mean of each sample. Therefore, there is no variability between the means of the samples, resulting in SS(between) = 0. However, there is still variability within each sample, resulting in SS(within) > 0.
(b) An example of data with SS(between) > 0 and SS(within) = 0 could be the following:
Sample 1: 1, 2, 3, 4, 5
Sample 2: 6, 7, 8, 9, 10
Sample 3: 11, 12, 13, 14, 15
In this example, the means of each sample are all the same (8), but the values within each sample are all different from each other. Therefore, there is variability between the means of the samples, resulting in SS(between) > 0. However, there is no variability within each sample, resulting in SS(within) = 0.
To know more about sample Visit:
https://brainly.com/question/28196409
#SPJ1
.) Suppose college students produce 650 pounds of solid waste each year, on average. Assume that the distribution of waste per college student is normal with a mean of 650 pounds and a standard deviation of 20 pounds. What is the probability that a randomly selected student produces either less than 620 or more than 700 pounds of solid waste
Answers
Answer:
0.073 = 7.3% probability that a randomly selected student produces either less than 620 or more than 700 pounds of solid waste
Step-by-step explanation:
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Mean of 650 pounds and a standard deviation of 20 pounds.
This means that \(\mu = 650, \sigma = 20\)
What is the probability that a randomly selected student produces either less than 620 or more than 700 pounds of solid waste?
Less than 620:
pvalue of Z when X = 620. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{620 - 650}{20}\)
\(Z = -1.5\)
\(Z = -1.5\) has a pvalue of 0.0668
More than 700:
1 subtracted by the pvalue of Z when X = 700. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{700 - 650}{20}\)
\(Z = 2.5\)
\(Z = 2.5\) has a pvalue of 0.9938
1 - 0.9938 = 0.0062
Total:
0.0668 + 0.0062 = 0.073
0.073 = 7.3% probability that a randomly selected student produces either less than 620 or more than 700 pounds of solid waste
3. Determine f(2,5) and (4,2) are solutions to the system of inequalities both algebraically and graphically. Show your work algebraically. Graphically, draw and shade both inequalities. Then, plot each ordered pair to confirm the answers you found algebraically.
y<1÷2 x+4
x+2y≥6

Answers
The graph showing the points is attached
The solutions are shown algebraically below
(2,5) is not a solution for y < x/2 + 4 (2,5) is a solution for x + 2y ≥ 6(4,2) is a solution for y < x/2 + 4(4,2) is a solution for x + 2y ≥ 6How to show the solutions algebraicallyThe solutions are f(2,5) and (4,2)
when the x or y part of the solution is substituted in the equation if the values is in line with the equation then the solution is correct
using f(2,5)
y < 1÷2x+4 = y < x/2 + 4
y < 2/2 + 4
y < 5
This is not a solution since y should be less than 5 not equal to 5
x + 2y ≥ 6 ⇒ x ≥ 6 - 2y
⇒ x ≥ 6 - 2 * 5
x ≥ 6 - 10
x ≥ -4
this is a solution 2 ≥ -4
using f(4,2)
y < x/2 + 4
y < 4/2 + 4
y < 6
This is a solution since 4 < 6
x + 2y ≥ 6 ⇒ x ≥ 6 - 2y
⇒ x ≥ 6 - 2 * 2
x ≥ 6 - 4
x ≥ 2
this is is a solution since 4 ≥ 2
Learn more about inequality graphs :
https://brainly.com/question/29244324
#SPJ1

The equation C=24n+2 represents the cost
Answers
Jim did not buy any tickets (n_Jim = 0).
Larry bought 7 more tickets than Jim.
To determine the number of tickets Larry bought more than Jim, we need to find the values of n for Larry and Jim's ticket purchases.
For Larry:
Let's substitute C = $170 into the equation C = 24n + 2 and solve for n:
$170 = 24n + 2
Subtracting 2 from both sides:
$168 = 24n
Dividing both sides by 24:
n = 7
For Jim:
We can calculate the number of tickets Jim bought by subtracting 12 from Larry's number of tickets:
n_Jim = n_Larry - 12
n_Jim = 7 - 12
n_Jim = -5
Since we cannot have a negative number of tickets, we can conclude that Jim did not buy any tickets (n_Jim = 0).
To find the difference in the number of tickets bought, we subtract the number of tickets Jim bought from the number of tickets Larry bought:
n_difference = n_Larry - n_Jim
n_difference = 7 - 0
n_difference = 7
Therefore, Larry bought 7 more tickets than Jim.
for such more question on quantity
https://brainly.com/question/29792134
#SPJ8
Question
The equation C=24n+2 represents the cost, C, in dollars, of buying n tickets to a play. J $170. How many more tickets did Larry buy than Jim? 12
If it takes 2men 11 days to dig 7 well, how many days should 7men dig 21well
Answers
7 men should be able to dig 21 wells in approximately 4.7 days.
How to determine the number of daysFrom the question, we have the following parameters that can be used in our computation:
If it takes 2men 11 days to dig 7 well, How many days should 7men dig 21wellWe can use the formula:
Number of days = (number of wells * number of days per well) / number of men.
So, we have
Number of days per well for 2 men:
11 days / 7 wells = 1.5714 days per well.
Using the above as a guide, we have the following:
the number of days for 7 men to dig 21 wells:
21 wells * 1.5714 days per well / 7 men = 4.7142days.
Hence, the number of days is 4.7 days.
Read more about rates at
https://brainly.com/question/24178013
#SPJ1
When f(x) is divided by x + 4 the quotient is x2+5x−3+2x+4. What is f(−4)?
Answers
=> f(-4)=((-4)2+5(-4)-3+2*(-4)+4)(-4+4)=0
F(-4)=0
For each ordered pair, determine whether it is a solution to the system of equations.
-3x+2y=5
y=8x-4
(x, y)
(0, -4)
(-3,5)
(1,4)
(-7, - 8)
Is it a solution?
Yes
O
O
O
No
O
X
Ś
Answers
An ordered pair which is a solution to the given system of linear equations is: (1, 4).
How to determine the solution?In order to determine which ordered pairs are valid and true solutions based on the given system of linear equations, we would have to test the given ordered pairs by substituting their values into the linear equations as follows;
For ordered pair (0, -4), we have:
-3x + 2y = 5
-3(0) + 2(-4) = 5
0 - 8 = 5
-8 = 5 (No)
For ordered pair (-3, 5), we have:
-3x + 2y = 5
-3(-3) + 2(5) = 5
9 + 10 = 5
19 = 5 (No)
For ordered pair (1, 4), we have:
-3x + 2y = 5
-3(1) + 2(4) = 5
-3 + 8 = 5
5 = 5 (Yes)
For ordered pair (1, 4), we have:
y = 8x - 4
4 = 8(1) - 4
4 = 4 (Yes).
For ordered pair (-7, -8), we have:
-3x + 2y = 5
-3(-7) + 2(-8) = 5
21 - 16 = 5
5 = 5 (Yes)
For ordered pair (-7, -8), we have:
y = 8x - 4
-8 = 8(-7) - 4
-8 = -58 (No).
Read more on ordered pairs here: brainly.com/question/12179097
#SPJ1
(02.02 MC)
Joel has a small deposit to save and is looking for an account that offers a high rate of return. He
does not need to have easy access to the money, and he doesn't mind taking a risk. Which of the
following options would best suit his needs?
Money Market account
Traditional savings account
Traditional checking account
Certificate of deposit
Answers
Answer:
Money Market account
Step-by-step explanation:
Money Market accounts typically allow you to earn money at a higher interest rate than other types of savings accounts.
2. Here is a linear equation in two variables:2x + 4y - 31 = 1232a. Solve for x.*A. x = 77-2yB. x = 2y - 77C. x = 154 - 4yD. x = 154 - 2y2b. Solve for y."
Answers
2a) x = 77 - 2y (option A)
2b) y = 77/2 - x/2
Explanation:2a) 2x + 4y - 31 = 123
To solve for x, first we need to collect like terms
Add 31 to both sides:
2x + 4y - 31 + 31 = 123 + 31
2x + 4y = 154
Next we move 4y to the other side by subtracting 4y from both sides:
2x + 4y - 4y = 154 - 4y
2x = 154 - 4y
Divide both sides by 2:
2x/2 = 1/2 (154 - 4y)
x = 154/2 - 4y/2
x = 77 - 2y (option A)
2b) To solve for y using the first equation, we will collect like terms
2x + 4y - 31 = 123
Add 31 to both sides:
2x + 4y - 31 + 31 = 123 + 31
2x + 4y = 154
subtract 2x from both sides:
2x - 2x + 4y = 154 - 2x
4y = 154 - 2x
divide both sides by 4:
\(\begin{gathered} \frac{4y}{4}\text{ = }\frac{1}{4}(154\text{ - 2x)} \\ y\text{ = }\frac{154}{4}\text{ - }\frac{2x}{4} \\ y\text{ = }\frac{77}{2}-\frac{x}{2} \end{gathered}\)leg 1: is 5 and leg 2: is 12 what is the hypotenuse
Answers
Answer:
13
Step-by-step explanation:
Hypotenuse is c
so c^2 = a^2 + b^2
c^2 = 5^2 + 12^2
c^2 = 25 + 144 = 169
c^2 = 13^2
c = 13
Joe is asked to prove that the sum of the interior angles (, , and ) of the triangle he has drawn equals 180°. His triangle is represented in the diagram above, and his work is shown below.
Answers
The angles <1, <2, and <3 will not add up to 180 degrees. The angles <1 and <2 are alternate interior angles, and the angles <2 and <3 are also alternate interior angles, AB is parallel to CD.
What is angle sum property of triangle?The angle sum property of a triangle states that the sum of the interior angles of a triangle is always equal to 180 degrees. This means that if you measure the angles inside any triangle and add them up, the result will always be 180 degrees. This property holds true for all types of triangles, whether they are equilateral, isosceles, or scalene.
To understand this property, consider a triangle ABC with interior angles angle A, angle B, and angle C. If we draw a line segment from vertex A to a point D on side BC such that it is parallel to the side AB, then we can see that angle A and angle C are alternate interior angles of the parallel lines AB and CD. Similarly, angle B and angle C are alternate interior angles of the parallel lines BC and AD.
To know more about isosceles, visit:
https://brainly.com/question/9872652
#SPJ1

fill in the mission numbers to make the fractions equivalent. 1/2 and /8= 4/12 and /60= 2/3 and /12= 4/4 and /8=
Answers
To make the fractions equivalent, we need to find the missing numerators that would make them equal. Let's fill in the missing numerators:
1/2 and __/8
To make the fractions equivalent, we can multiply both the numerator and denominator of the first fraction by 4:
1/2 and 4/8
Now, the fractions are equivalent.
---
4/12 and __/60
To make the fractions equivalent, we can multiply both the numerator and denominator of the first fraction by 5:
4/12 and 20/60
Now, the fractions are equivalent.
---
2/3 and __/12
To make the fractions equivalent, we can multiply both the numerator and denominator of the first fraction by 4:
2/3 and 8/12
Now, the fractions are equivalent.
---
4/4 and __/8
To make the fractions equivalent, we can multiply both the numerator and denominator of the first fraction by 2:
4/4 and 8/8
Now, the fractions are equivalent.
There are two numbers that have a sum of 47. Three times the lesser
number is equal to 9 more than the greater number. What are the
numbers?
Answers
Answer:
The numbers are 14 and 33---------------
Let the numbers be s and l.
We are given that:
Sum of the two is 47 and 3 times the lesser number is equal to 9 more than the greater number.Set up equations:
s + l = 473s = l + 9Eliminate l:
l = 47 - s and l = 3s - 9Solve for s:
47 - s = 3s - 93s + s = 47 + 94s = 56s = 14Find l:
l = 47 - 14l = 33What is 6 divided by 2 ( 1+2 ) = ?
Answers
ANSWER;
6/ 2(1+2)
= 6/ 2(3)
= 6/ 2X3
= 6/6
= 1
Answer:
6 ÷ 2 [1 + 2]
= 6 ÷ 2 + 4
= 6 ÷ 6
= 1
A basket had 15 mangoes. A monkey came and took
away two-fifths of the mangoes. How many mangoes
were left in the basket
Answers
Answer: There are 9 mangoes left in the basket.
Step-by-step explanation:
(2/5) * 15 = 6.
15 - 6 = 9.
The quality control manager at a factory records the number of equipment breakdowns each day. Let the random variable Y represent the number of breakdowns in one day. The standard deviation of Y is 0.28. Which of the following is the best interpretation of the standard deviation? A. The number of breakdowns on a randomly selected day is expected to be 0.28. B. The number of breakdowns on a randomly selected day will be 0.28 away from the mean. C. The average number of breakdowns per day for a random sample of days is expected to be 0.28 D. On average, the number of breakdowns per day varies from the mean by about 0.28. E. The number of breakdowns per day for a random sample of days is expected to be 0.28 away from the mean.
Answers
The correct option is (D). On average, the number of breakdowns per day varies from the mean by about 0.28.
Because standard deviation represents the typical distance between each data point and the mean.
The variability in a dataset is condensed into a single value called the standard deviation (SD). It shows the typical separation between the mean and each data point. Smaller values show that the data points are more evenly distributed around the mean, indicating that the dataset's values are generally stable.The average distance between each data point and the mean is known as the mean absolute deviation of a dataset. It offers us a sense of how variable a dataset is.
A discrete random variable's variance and standard deviation can be seen as measurements of the variability of the values the random variable assumes throughout the course of an experiment's multiple trials.So, the correct answer is On average, the number of breakdowns per day varies from the mean by about 0.28.
For more such questions on standard deviation
https://brainly.com/question/23907081
#SPJ4
Jane spent 2/5 of her money on games. She had $120 remaining. What was the cost of the games Jane bought?
Answers
Answer:
i think it would be $80 (brainliest??)
Step-by-step explanation:
jane had a total of $200 BEFORE she spent on 2 games
1. $40
2. $40
3. $40
4. $40
5.$40
2 games = $80
3 games = $120 (money she had left)
Which the following expressions is equivalent(
a + b)(a-b)?
Answers
Answer:
Step-by-step explanation:
(a+b)(a-b)=a^2-b^2
Find the measure of e . A. 88 B. 46 C. 44 D. 90

Answers
Answer:
The answer is A. 88.
Step-by-step explanation:
To solve for the measure of angle ( \(e\) ), start by noticing that 92 degrees and ( \(e\) ) sum up to 180 degrees, which makes them supplementary angles.
Two angles are said to be supplementary angles if they add up to 180 degrees. Supplementary angles form a straight angle (180 degrees) when they are put together. In other words, angle 1 and angle 2 are supplementary, if Angle 1 + Angle 2 = 180 degrees.
Since angle 92 degrees and angle ( \(e\) ) sum up to 180 degrees, the equation will look like \(92\)°\(+e=180\)°. To solve the equation, start by subtracting 92 degrees from both sides, and the equation will look like \(e=88\)°. The final answer will be that the measure of angle ( \(e\) ) is 88 degrees.
Answer:
88
Step-by-step explanation:
If the lengths of two adjacent sides of a parallelogram area a and b, and if the acute angle formed by these two sides is theta, show that the product of the lengths of the two diagonals is given by the expression (a^2 + b^2)^2 - 4a^2b^2cos^2theta
Answers
√(a² + b²)² - 4a²b²cos²θ is the product of the lengths of the two diagonals is given by the expression.
What is a mathematical expression?
A mathematical expression is a phrase that includes at least two numbers or variables, at least one arithmetic operation, and the expression itself. This mathematical operation may be addition, subtraction, multiplication, or division.
An expression's structure is as follows: Number/variable, Math Operator, Number/Variable is an expression.
we have AB as a, AD as b and the angle between them is theta.
So using the cosine rule, we have
BD = √a² + b² - 2abcosθ
So now consider the triangle ABC
Here AB is a, BC is b and the angle is 180-theta
So using cosine rule, we get AC as
AC = √a² + b² - 2abcosθ( 180 - θ )
AC = √a² + b² - 2ab(-cosθ )
AC = √a² + b² - 2abcosθ
Now we have the two diagonals AC and BD. So multiplying, we get
AC × BD = √a² + b² + 2abcosθ × √a² + b² - 2abcosθ
Simplifying, we get
AC × BD = √(a² + b² + 2abcosθ) × (√a² + b² - 2abcosθ)
AC × BD = √(a² + b²)² - (2abcosθ)²
AC × BD = √(a² + b²)² - 4a²b²cos²θ
Learn more about the expression
brainly.com/question/29052794
#SPJ4
20 PTS LOOK AT PIC FOR QUESTION WILL MARK BRAINILEST clc

Answers
Answer:
295 square feet
Step-by-step explanation:
Break the figure up into 3 rectangles, and then find the area of each rectangle and add all areas together.
15*3=45
19*10=190
15*4=60
45+190+60=295
Answer:26 *15*4*5*3=23400
Step-by-step explanation: Area is measured in square units such as square inches, square feet or square meters. To find the area of a rectangle, multiply the length by the width. The formula is: A = L * W where A is the area, L is the length, W is the width, and * means multiply.