If f(x) = 3x - 2 then what is f(10)?
Answers
Answer:
f(10) = 3(10) - 2 = 28
Step-by-step explanation:
Related Questions
y+4x=-5
2y=-8x-20
Is it no solution or exactly one solution?
PLS HELP
Answers
Answer:
there are no solutions in the equation :)
How to solve 342x8 the easiest way

Answers
Answer:
Step-by-step explanation:
8x2 = 16
8x4= 32 (since its the 2nd one meaning its in the tenth place add 1 Zero, 10) making it 320
8x3 =24 (since its hundredths place add 2 Zeros 100) making 2400
2400+ 320+ 16= 2736
The answer is 2737
n3=8/125 for n n= ???
Answers
Answer:
2/25
Step-by-step explanation:
\(n^3 = \frac{8}{125}\)
\(n^3 = (\frac{2}{5})^3\)
\(n = \sqrt[3]{n^3} = \sqrt[3]{(\frac{2}{25})^3}\)
\(n = \sqrt[3]{(\frac{2}{25})^3}\)
\(n = \frac{2}{25}\)
if the minimum amount of weight you could add to a 10 pound backpack someone was wearing (with them noticing) was 1 pound, how much would have to be added to a 100 pound backpack for them to notice?
Answers
Answer:
10 pounds
Step-by-step explanation:
given ratio weight:added weight=10:1
100:x=10:1
100/x=10/1
solving for x
100=10x
x=10
What is the remainder when x 3 1 is divided by x 3 x 1?
Answers
The remainder when x³ - 1 is divided by (x + 3) is -28
How to determine the remainder of the polynomial division?The functions are given as
x 3 1 is divided by x 3
Rewrite them as
f(x) = x³ - 1 is divided by (x + 3)
Set the divisor to 0
So, we have
x + 3 = 0
Determine the value of x
This gives
x = -3
By the remainder theorem
Substitute x = -3 in the function f(x)
So, we have
f(-3) = (-3)³ - 1
Evaluate the expression
f(-3) = -28
By the remainder theorem, this represents the remainder
Read more about remainder at
brainly.com/question/14130807
#SPJ1
Sharon is paving a rectangular concrete driveway on the side of her house. The area of the driveway is , and the length of the driveway is . What is the width of the driveway in terms of x
Answers
The width of the driveway is 5x-2 and the height of the carport is 6x+1.
What is a rectangle?a plane figure with four straight sides and four right angles, especially one with unequal adjacent sides, in contrast to a square.
The area of a rectangle is given by length × width. Since the area is 5x²+43x-18 and the length is x+9, to find the width, we divide:
he first term of the quotient will be the number of times x goes into 5x². It goes 5x times; multiply this by the divisor, and we have 5x²+45x to write under the first two terms of the dividend. Subtracting these, we have -2x left over bring down the -18. The second term of the quotient will be the number of times x+9 goes into -2x-18, it goes -2 times. Multiply this by the divisor, and we have -2x-18 with no remainder. This gives the quotient 5x-2.
The volume of the carport is given by the area of the base × height, since the volume is 48x³+68x²-8x-3 and the area of the base is 8x²+10x-3, we divide to get the height.
The first term of the quotient will be the number of times 8x² goes into 48x³. It goes 6x times; multiply this by the divisor and we have 48x³+60x² to write under the first two terms of the dividend.
Subtract these and we have 8x²+10x left over bring down the -3. The second term of the quotient will be the number of times 8x² goes into 8x²; it goes 1 time. Multiply this by the divisor and we have 8x²+10x-3 with no remainder. This makes the height 6x-3.
Hence, The width of the driveway is 5x-2 and the height of the carport is 6x+1.
To learn more about rectangle from the given link:
https://brainly.com/question/8614122
#SPJ4

express your answer as a polynomial in a standard form.
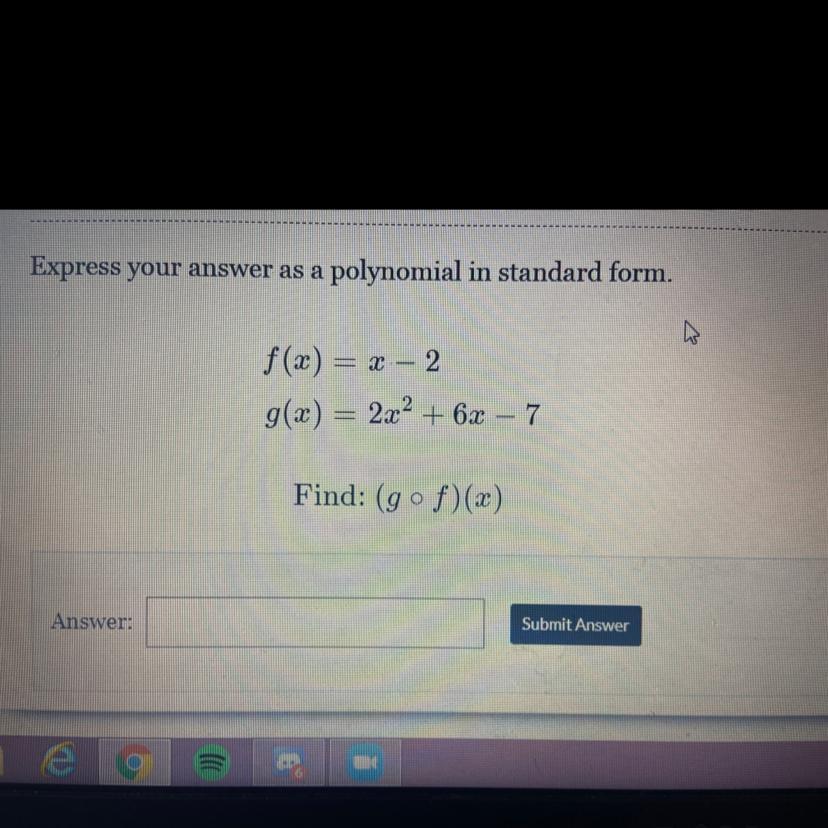
Answers

Consider the simplified Mastermind game in which there are three positions and three colors of pegs. Find an optimal first guess for this game. A guess is optimal if for some number k, all possible scores of the guess leave at most k possible secret codes and some possible score of any other guess leaves at least k possible secret codes.
Answers
The optimal first guess for the simplified Mastermind game with three positions and three colors of pegs is "ABC" (where A, B, and C represent the three different colors).
In the simplified Mastermind game, each position can be filled with any of the three available colors. Therefore, there are a total of 3^3 = 27 possible secret codes.
To find the optimal first guess, we need to choose a guess that maximizes the number of possible secret codes it eliminates. The guess "ABC" covers all the available colors and positions, ensuring that no matter the secret code, it will match at least one peg.
By selecting "ABC" as the first guess, we eliminate a maximum number of secret codes. For any possible score, there will always be at most 18 remaining possible secret codes (since we eliminate 9 possibilities). This is the highest elimination rate among all possible first guesses.
Hence, "ABC" is the optimal first guess in the simplified Mastermind game, as it maximizes the elimination of possible secret codes and provides the best starting point for subsequent guesses.
To know more game of Mastermind, visit:
https://brainly.com/question/32884539
#SPJ11
Find an equation of the tangent line to the following curve at the given point. y = e6x cos x, (0, 1)
Answers
An equation of the tangent line to curve [y = e⁶ˣ cos x] at the given point (0, 1) is y = x + 6.
What is tangent line?At a given point, the tangent line of a curve is a line that really just contacts the curve (function). In calculus, the tangent line may connect the curve at any other point(s), and it may also cross the graph at any other point(s).
Now, as per the given question;
Because of this, point (0,1) is a tangent point;
y = f((0) = e⁰cos0 = 1.
We differentiate to get the slope of the tangent line m. Tangent line equation:
y' = 6e⁶ˣcosx - e⁶ˣ sinx;
Thus, the slope of the curve becomes;
m = f'(0) = 6.
Substituting the values of slope and coordinates (0, 1).
y = 6 + 1(x - 0),
Simplifying the equation.
y = x + 6
Thus, the equation of the tangent line to the given curve is y = x + 6.
To know more about the tangent line, here
https://brainly.com/question/6617153
#SPJ4
What is the volume of a hemisphere with a radius of 44. 9 m, rounded to the nearest tenth of a cubic meter?.
Answers
The volume of a hemisphere with a radius of 44.9 m is approximately 189582.2 cubic meters, rounded to the nearest tenth.
To calculate the volume of a hemisphere, you can use the formula
V = (2/3)πr^3
where V is the volume, π is pi (approximately 3.14), and r is the radius. In this case, r = 44.9 m.
So, (2/3)π(44.9)^3 = 189582.234 cubic meters.
This is the exact volume, but since the question asked for the volume rounded to the nearest tenth, the final answer would be 189582.234 cubic meters. It's worth mentioning that a hemisphere is half of a sphere, thus, the volume of a full sphere with a radius of 44.9 m would be double of this value.
To know more about hemisphere click below:
https://brainly.com/question/13625065#
#SPJ4
Pls someone help me please

Answers
2
1
3
5/8 = 0.625
1/3 = 0.3333...
17/24 = 0.70833333
−8.3=d+4.7
Pls Help me
Answers
-d = 13
d = -13
Answer this CORRECTLY

Answers
Answer:
call Alex hanna 999 231 7767
Step-by-step explanation:
What value should go in the empty box to complete the calculation for finding the product of 62.834 × 0.45? A)2,213,360 B)2,313,360 C)2,413,360 D)2,513,360
Answers
Answer:
28.27530
Step-by-step explanation:
Given the expression 62.834 × 0.45, to solve this expression, first we need to convert it to fraction
62.834 = 62834/1000
0.45 = 45/100
Take the product if the resulting fraction:
62.834 × 0.45 = 62834/1000 × 45/100
= (62834×45)/1000×100
= 2,827,530/100,000
= 28.27530
Answer:28.27530
Step-by-step explanation:Given the expression 62.834 × 0.45, to solve this expression, first we need to convert it to fraction
62.834 = 62834/1000
0.45 = 45/100
Take the product if the resulting fraction:
62.834 × 0.45 = 62834/1000 × 45/100
= (62834×45)/1000×100
= 2,827,530/100,000
= 28.27530
If a bike normally costs $150 but it is marked up
100% due to an increase in demand. How much
would it cost? *
Answers
Answer:
300
Step-by-step explanation:
100% of 150 is literally 150, add those together and you get 300.
Answer:
the answer is $300
Step-by-step explanation: when increasing by 100% it is the same as multiplying by 2
Suppose the function y(t) satisfies the differential equation y ′(t)+a(t)y(t)=b(t) where the functions a(t) and b(t) are not constant. Define the function z(t)=y(4t). Which of the following differential equations is z(t) a solution to? z ′ (t)+4a(4t)z(t)=4b(4t)
z ′ (t)+4a(t)z(t)=4b(t)
z ′ (t)+a(4t)z(t)=b(4t)
z ′ (t)+a(t)z(t)=b(t)
Answers
z(t) satisfies the differential equation: z'(t) + 4a(4t)z(t) = 4b(4t)
So, the correct option is z'(t) + 4a(4t)z(t) = 4b(4t).
To determine which differential equation z(t) satisfies, let's differentiate z(t) with respect to t and substitute it into the given differential equation.
We have z(t) = y(4t), so differentiating z(t) with respect to t using the chain rule gives:
z'(t) = (dy/dt)(4t) = 4(dy/dt)(4t)
Now let's substitute z(t) = y(4t) and z'(t) = 4(dy/dt)(4t) into the differential equation y'(t) + a(t)y(t) = b(t):
4(dy/dt)(4t) + a(4t)y(4t) = b(4t)
Now, let's compare the coefficients of each term in the resulting equation:
For the first option, z'(t) + 4a(4t)z(t) = 4(dy/dt)(4t) + 4a(4t)y(4t), we can see that it matches the form of the resulting equation.
Therefore, z(t) satisfies the differential equation:
z'(t) + 4a(4t)z(t) = 4b(4t)
So, the correct option is z'(t) + 4a(4t)z(t) = 4b(4t).
Learn more about differential equation
brainly.com/question/32645495
#SPJ11
a wall that is 12 feet wide and 10 feet high is to be painted. a blackboard that is 5 feet wide and 3 feet high is affixed to the wall and is the only portion of the wall that will not be painted.
Answers
The area of the wall that will be painted is 105 square feet. To find the area of the wall that will be painted, we need to subtract the area of the blackboard from the total area of the wall.
The total area of the wall is calculated by multiplying its width by its height:
Total area of wall = 12 feet * 10 feet = 120 square feet
The area of the blackboard is calculated by multiplying its width by its height:
Area of blackboard = 5 feet * 3 feet = 15 square feet
To find the area of the wall that will be painted, we subtract the area of the blackboard from the total area of the wall:
Area of painted wall = Total area of wall - Area of blackboard
Area of painted wall = 120 square feet - 15 square feet
Area of painted wall = 105 square feet
The area of the wall that will be painted is 105 square feet.
To know more about area , visit;
https://brainly.com/question/1631786?
#SPJ11
Evaluate the expression.

Answers
Answer:
1/125 (0.008)
Step-by-step explanation:
1/(5⁻³) * 1/(5⁶) = 5³ / 5⁶ = 1 / 5³ = 1 /125
What is an equation of the line that passes through the point (−8,−1) and is parallel to the line x-4y=4x
Answers
Answer:
y = -3/4x - 7
Step-by-step explanation:
Parallel lines have the same slope.
Solve for y in the equation to find the slope.
x - 4y = 4x
-4y = -x + 4x
-4y = 3x
y = 3/-4 x = -3/4x So the slope is -3/4 which is the coefficient of the
x term
Substitute the slope(m) = -3/4 and point (-8, -1) into y = mx + b to solve for "b"
y = mx + b
-1 = -3/4(-8) + b
-1 = 6 + b
-1 - 6 = b
-7 = b
The equation of the new line: y = mx + b
y = -3/4x - 7
Find the first and second derivatives of the function. (Factor your answer completely.)
g(u) = u(2u − 3)^3
g ' (u) = g'' (u) =
Answers
The first derivative of the function `g(u) = u(2u - 3)^3` is `g'(u) = 6u(2u - 3)^2 + (2u - 3)^3`. The second derivative of the function is `g''(u) = 12(u - 1)(2u - 3)^2`.
Given function: `g(u)
= u(2u - 3)^3`
To find the first derivative of the given function, we use the product rule of differentiation.`g(u)
= u(2u - 3)^3`
Differentiating both sides with respect to u, we get:
`g'(u)
= u * d/dx[(2u - 3)^3] + (2u - 3)^3 * d/dx[u]`
Using the chain rule of differentiation, we have:
`g'(u)
= u * 3(2u - 3)^2 * 2 + (2u - 3)^3 * 1`
Simplifying:
`g'(u)
= 6u(2u - 3)^2 + (2u - 3)^3`
To find the second derivative, we differentiate the obtained expression for
`g'(u)`:`g'(u)
= 6u(2u - 3)^2 + (2u - 3)^3`
Differentiating both sides with respect to u, we get:
`g''(u)
= d/dx[6u(2u - 3)^2] + d/dx[(2u - 3)^3]`
Using the product rule and chain rule of differentiation, we have:
`g''(u)
= 6[(2u - 3)^2] + 12u(2u - 3)(2) + 3[(2u - 3)^2]`
Simplifying:
`g''(u)
= 12(u - 1)(2u - 3)^2`.
The first derivative of the function `g(u)
= u(2u - 3)^3` is `g'(u)
= 6u(2u - 3)^2 + (2u - 3)^3`. The second derivative of the function is `g''(u)
= 12(u - 1)(2u - 3)^2`.
To know more about derivative visit:
https://brainly.com/question/29144258
#SPJ11
The first derivative of g(u) is g'(u) = (2u - 3)³ + 6u(2u - 3)², and the second derivative is g''(u) = 12(2u - 3)² + 12u(2u - 3).
Using the product and chain ruleFirst, let's find the first derivative:
g'(u) = (2u - 3)³ * d(u)/du + u * d/dx[(2u - 3)³]
Using the chain rule, we can differentiate (2u - 3)³ and u as follows:
d(u)/du = 1
d/dx[(2u - 3)³] = 3(2u - 3)² * d(2u - 3)/du
= 3(2u - 3)² * 2
Plugging these values back into the equation for g'(u), we have:
g'(u) = (2u - 3)² + u * 3(2u - 3)² * 2
= (2u - 3)³ + 6u(2u - 3)²
Simplifying the expression, we have:
g'(u) = (2u - 3)³ + 6u(2u - 3)²
Now, let's find the second derivative:
g''(u) = d/dx[(2u - 3)³ + 6u(2u - 3)²]
Using the chain rule and product rule, we can differentiate each term:
d/dx[(2u - 3)³] = 3(2u - 3)² * d(2u - 3)/du
= 3(2u - 3)² * 2
d/dx[6u(2u - 3)²] = 6(2u - 3)² + 6u * d/dx[(2u - 3)²]
= 6(2u - 3)² + 6u * 2(2u - 3)
The Second derivativePlugging these values back into the equation for g''(u), we have:
g''(u) = 3(2u - 3)² * 2 + 6(2u - 3)² + 6u * 2(2u - 3)
= 6(2u - 3)² + 6(2u - 3)² + 12u(2u - 3)
= 12(2u - 3)² + 12u(2u - 3)
Simplifying the expression further, we have:
g''(u) = 12(2u - 3)² + 12u(2u - 3)
Therefore, the first derivative of g(u) is g'(u) = (2u - 3)³ + 6u(2u - 3)², and the second derivative is g''(u) = 12(2u - 3)² + 12u(2u - 3).
Learn more on differentiation : https://brainly.com/question/25081524
#SPJ4
please find the result !

Answers
Answer:
\( \displaystyle - \frac{1}{2} \)
Step-by-step explanation:
we would like to compute the following limit:
\( \displaystyle \lim _{x \to 0} \left( \frac{1}{ \ln(x + \sqrt{ {x}^{2} + 1} ) } - \frac{1}{ \ln(x + 1) } \right) \)
if we substitute 0 directly we would end up with:
\( \displaystyle\frac{1}{0} - \frac{1}{0} \)
which is an indeterminate form! therefore we need an alternate way to compute the limit to do so simplify the expression and that yields:
\( \displaystyle \lim _{x \to 0} \left( \frac{ \ln(x + 1) - \ln(x + \sqrt{ {x}^{2} + 1 } }{ \ln(x + \sqrt{ {x}^{2} + 1} ) \ln(x + 1) } \right) \)
now notice that after simplifying we ended up with a rational expression in that case to compute the limit we can consider using L'hopital rule which states that
\( \rm \displaystyle \lim _{x \to c} \left( \frac{f(x)}{g(x)} \right) = \lim _{x \to c} \left( \frac{f'(x)}{g'(x)} \right) \)
thus apply L'hopital rule which yields:
\( \displaystyle \lim _{x \to 0} \left( \frac{ \dfrac{d}{dx} \ln(x + 1) - \ln(x + \sqrt{ {x}^{2} + 1 } }{ \dfrac{d}{dx} \ln(x + \sqrt{ {x}^{2} + 1} ) \ln(x + 1) } \right) \)
use difference and Product derivation rule to differentiate the numerator and the denominator respectively which yields:
\( \displaystyle \lim _{x \to 0} \left( \frac{ \frac{1}{x + 1} - \frac{1}{ \sqrt{x + 1} } }{ \frac{ \ln(x + 1)}{ \sqrt{ {x}^{2} + 1 } } + \frac{ \ln(x + \sqrt{x ^{2} + 1 } }{x + 1} } \right) \)
simplify which yields:
\( \displaystyle \lim _{x \to 0} \left( \frac{ \sqrt{ {x}^{2} + 1 } - x - 1 }{ (x + 1)\ln(x + 1 ) + \sqrt{ {x}^{2} + 1} \ln( x + \sqrt{ {x }^{2} + 1} ) } \right) \)
unfortunately! it's still an indeterminate form if we substitute 0 for x therefore apply L'hopital rule once again which yields:
\( \displaystyle \lim _{x \to 0} \left( \frac{ \dfrac{d}{dx} \sqrt{ {x}^{2} + 1 } - x - 1 }{ \dfrac{d}{dx} (x + 1)\ln(x + 1 ) + \sqrt{ {x}^{2} + 1} \ln( x + \sqrt{ {x }^{2} + 1} ) } \right) \)
use difference and sum derivation rule to differentiate the numerator and the denominator respectively and that is yields:
\( \displaystyle \lim _{x \to 0} \left( \frac{ \frac{x}{ \sqrt{ {x}^{2} + 1 } } - 1}{ \ln(x + 1) + 2 + \frac{x \ln(x + \sqrt{ {x}^{2} + 1 } ) }{ \sqrt{ {x}^{2} + 1 } } } \right) \)
thank god! now it's not an indeterminate form if we substitute 0 for x thus do so which yields:
\( \displaystyle \frac{ \frac{0}{ \sqrt{ {0}^{2} + 1 } } - 1}{ \ln(0 + 1) + 2 + \frac{0 \ln(0 + \sqrt{ {0}^{2} + 1 } ) }{ \sqrt{ {0}^{2} + 1 } } } \)
simplify which yields:
\( \displaystyle - \frac{1}{2} \)
finally, we are done!
9514 1404 393
Answer:
-1/2
Step-by-step explanation:
Evaluating the expression directly at x=0 gives ...
\(\dfrac{1}{\ln(\sqrt{1})}-\dfrac{1}{\ln(1)}=\dfrac{1}{0}-\dfrac{1}{0}\qquad\text{an indeterminate form}\)
Using the linear approximations of the log and root functions, we can put this in a form that can be evaluated at x=0.
The approximations of interest are ...
\(\ln(x+1)\approx x\quad\text{for x near 0}\\\\\sqrt{x+1}\approx \dfrac{x}{2}+1\quad\text{for x near 0}\)
__
Then as x nears zero, the limit we seek is reasonably approximated by the limit ...
\(\displaystyle\lim_{x\to0}\left(\dfrac{1}{x+\dfrac{x^2}{2}}-\dfrac{1}{x}\right)=\lim_{x\to0}\left(\dfrac{x-(x+\dfrac{x^2}{2})}{x(x+\dfrac{x^2}{2})}\right)\\\\=\lim_{x\to0}\dfrac{-\dfrac{x^2}{2}}{x^2(1+\dfrac{x}{2})}=\lim_{x\to0}\dfrac{-1}{2+x}=\boxed{-\dfrac{1}{2}}\)
_____
I find a graphing calculator can often give a good clue as to the limit of a function.

find the area of the figure

Answers
Answer:
\(A=190\ cm^2\)
Step-by-step explanation:
The attached figure shows a parallelogram.
Base, \(b=15\dfrac{1}{5}\ yd=\dfrac{76}{5}\ yd\)
Height, \(h=12\dfrac{1}{2}\ yd=\dfrac{25}{2}\ yd\)
We need to find the area of the figure. The area of a parallelogram is given by :
\(A=b\times h\\\\A=\dfrac{76}{5}\times \dfrac{25}{2}\\\\A=190\ cm^2\)
So, the area of the figure is \(190\ cm^2\).
For the following scenarios, state the null hypothesis and the alternative hypothesis to be used when a hypothesis test is performed. Scenario i) After the Cold War, it was claimed that two of three Americans say that the chances of world peace are seriously threatened by the nuclear capabilities of other countries. Is there evidence that this proportion is actually different? To investigate this, a random sample of 400 Americans was taken, and it was found that only 248 hold this view. Scenario ii) JP wants to test whether at least 9% of gaming headsets have manufacturing flaws that make game-play impossible. A sample of 150 headsets revealed that 12 contained a defect. Scenario iii) The mean water temperature downstream from JP's Power Plant's cooling tower discharge pipe should be no more than 106°F. Past experience has indicated that the standard deviation of temperature is 2°F. The water temperature is measured on nine randomly chosen days, and the average temperature is found to be 99°F. 2. Suppose you were performing a hypothesis test, and you found the power for a given alternative to be 0.9382. Based only on the power of the test, would you believe that this is a good test procedure? Explain why or why not in 1-3 sentences.Previous question
Answers
Scenario i)
Null hypothesis: The proportion of Americans who say that the chances of world peace are seriously threatened by the nuclear capabilities of other countries is equal to two-thirds (66.67%).
Alternative hypothesis: The proportion of Americans who say that the chances of world peace are seriously threatened by the nuclear capabilities of other countries is different from two-thirds.
Scenario ii)
Null hypothesis: The proportion of gaming headsets with manufacturing flaws that make game-play impossible is less than 9%.
Alternative hypothesis: The proportion of gaming headsets with manufacturing flaws that make game-play impossible is at least 9%.
Scenario iii)
Null hypothesis: The mean water temperature downstream from JP's Power Plant's cooling tower discharge pipe is 106°F.
Alternative hypothesis: The mean water temperature downstream from JP's Power Plant's cooling tower discharge pipe is more than 106°F.
2. The power of a hypothesis test indicates the ability of the test to correctly reject the null hypothesis when the alternative hypothesis is true. A power of 0.9382 suggests that the test procedure has a high probability of detecting a true effect or difference. Therefore, based on the power of the test, it can be considered a good test procedure.
to more about proportion visit:
brainly.com/question/31010676
#SPJ11
find inverse equation for y=(x-3)^2
Answers
Answer:Rewrite the cartesian equation as a polar equation.
Rewrite the cartesian equation as a polar equation.r
Rewrite the cartesian equation as a polar equation.r2
Rewrite the cartesian equation as a polar equation.r2cos
Rewrite the cartesian equation as a polar equation.r2cos2
Rewrite the cartesian equation as a polar equation.r2cos2(
Rewrite the cartesian equation as a polar equation.r2cos2(θ
Rewrite the cartesian equation as a polar equation.r2cos2(θ)
Rewrite the cartesian equation as a polar equation.r2cos2(θ)−
Rewrite the cartesian equation as a polar equation.r2cos2(θ)−6
Rewrite the cartesian equation as a polar equation.r2cos2(θ)−6r
Rewrite the cartesian equation as a polar equation.r2cos2(θ)−6rcos
Rewrite the cartesian equation as a polar equation.r2cos2(θ)−6rcos(
Rewrite the cartesian equation as a polar equation.r2cos2(θ)−6rcos(θ
Rewrite the cartesian equation as a polar equation.r2cos2(θ)−6rcos(θ)
Rewrite the cartesian equation as a polar equation.r2cos2(θ)−6rcos(θ)−
Rewrite the cartesian equation as a polar equation.r2cos2(θ)−6rcos(θ)−r
Rewrite the cartesian equation as a polar equation.r2cos2(θ)−6rcos(θ)−rsin
Rewrite the cartesian equation as a polar equation.r2cos2(θ)−6rcos(θ)−rsin(
Rewrite the cartesian equation as a polar equation.r2cos2(θ)−6rcos(θ)−rsin(θ
Rewrite the cartesian equation as a polar equation.r2cos2(θ)−6rcos(θ)−rsin(θ)
Rewrite the cartesian equation as a polar equation.r2cos2(θ)−6rcos(θ)−rsin(θ)=
Rewrite the cartesian equation as a polar equation.r2cos2(θ)−6rcos(θ)−rsin(θ)=−
Rewrite the cartesian equation as a polar equation.r2cos2(θ)−6rcos(θ)−rsin(θ)=−9
Rewrite the cartesian equation as a polar equation.r2cos2(θ)−6rcos(θ)−rsin(θ)=−9Tap to view steps...
The quadratic function which is represented by the graph of a Parabola fails the Horizontal Line Test thus is not a one to one function. Therefore the inverse is not a function unless with restricted domain.
Edit: Adding the solution below to address update in the comments:
y
=
(
x
+
3
)
2
x
=
(
y
+
3
)
2
±
√
x
=
y
+
3
y
=
−
3
±
√
x
=> inverse relation
Restricting the domain: Recall that the domain and the range of the inverse function are the range and the domain of the original function respectively. The range of the original function in this case is
y
≥
0
, that should be the domain of the inverse function so for the inverse function we take the positive square root as follow:
f
−
1
(
x
)
=
−
3
+
√
x
=> this is the inverse function the domain and the range are:
domain:
x
≥
0
range:
y
≥
−
3
This means we need to restrict the domain of the original function to:
x
≥
−
3
in order for it to have an inverse function.
let $m/n$, in lowest terms, be the probability that a randomly chosen positive divisor of $10^{99}$ is an integer multiple of $10^{88}$. find $m n$.
Answers
The value of (m+n) is 634.
Probability is a way to gauge how likely something is to happen. Many things are difficult to forecast with absolute confidence. Using it, we can only make predictions about the likelihood of an event happening, or how likely it is.
Probability can vary from 0 to 1, with 0 being an impossibility and 1 denoting a certainty.
The probability formula is defined as the possibility of an event happening being equal to the ratio of the number of favorable outcomes and the total number of outcomes.
To get the multiples of \(10^{99}\)
we need to take \({(2)^{88}.........(2)^{99}}\) and \({(5)^{88}.........(5)^{99}}\)
there are 12*12= 144
Probability = 14/(100)² = 144/10000 = 9/625
Thus, m = 9 and n = 626
Hence, m+n = 9+625 =634
Therefore, The value of (m+n) is 634.
To know more about Probability visit: brainly.com/question/11234923
#SPJ4
How many real solutions does it have?
v² = -75
Answers
Answer:
None
Step-by-step explanation:
\(v^2=-75\) has the solution \(v=\pm \sqrt{-75}\), but it isn't real since you cannot take the square root of a negative number to produce that real output.
4. Which of the following formulas can be used to write 0.797979... as a fraction?
Answers
Answer:
The options are not shown, so i will answer this in a general way.
When we have a number like:
0.7979....
The steps to writing it as a fraction are the following ones:
1) First, you need to notice the repeating decimals.
In this case is easy to see that the repeating decimals are two, 7 - 9
2)we can multiply this number by 10^n, where n is the number of repeated decimals, in this case n = 2
10^2 = 100
then:
0.7979...*100 = 79.7979...
Now we can subtract the original number:
79.7979... - 0.7979 = 79
And this is equivalent to have:
0.7979..*100 - 0.7979... = 0.7979..*99 = 79
Then we know that if we multiply our number by 99, the outcome will be an integer.
Then we can multiply and divide by the same number (this is equivalent to multiply by one) as follows:
0.7979...*1 = 0.7979..*(99)/(99) = (0.7979..*99)/99 = 79/99
Then:
0.7979... = 79/99
Answer:
\(S_{inf.} - \frac{\frac{79}{100} }{1-\frac{1}{100} }\)
Pretend "inf." is the infinity symbol, I couldn't put the actual symbol. It's option B.
what is Nine hundred four thousandths in decimal form I will give 5 stars if your Correct I would like a explanation to if someone can do that
Answers
Answer:
0.904
Step-by-step explanation:
You want the decimal version of "nine hundred four thousandths".
Reading decimalsA decimal fraction is read (expressed in words) as the number to the right of the decimal point followed by the place value of the least-significant digit:
0.2 = "two tenths"
0.34 = "thirty-four hundredths"
0.904 = "nine hundred four thousandths"
0.0008 = "eight ten-thousandths"
FractionThe same reading applies to the number written as a fraction:
2/10 = "two tenths"
34/100 = "thirty-four hundredths"
904/1000 = "nine hundred four thousandths"
8/10000 = "eight ten-thousandths"
Each of these can be converted to a decimal by recognizing the meaning of the various parts of the fraction:
904/1000 = 904 × 1/1000
= 904 × 0.001 = 0.904
__
Additional comment
When reading a decimal number that has an integer part and a fractional part, the location of the decimal point is often signified by the word "and":
"nine hundred and four thousandths" = 900 + 0.004 = 900.004
This suggests you need to be somewhat careful with the use of "and" when pronouncing a decimal number.

Find the probability a randomly selected z-score is between -1 and 1.2. 0.7781 None of these 0.7019 0.7761 0.7263
Answers
To find the probability a randomly selected z-score is between -1 and 1.2, we need to use the standard normal distribution table.
A standard normal distribution table shows the area to the left of the z-score. To find the area between two z-scores, we need to find the area to the left of the larger z-score and subtract the area to the left of the smaller z-score. So, the probability that a randomly selected z-score is between -1 and 1.2 is given by: P(-1 ≤ z ≤ 1.2) = P(z ≤ 1.2) - P(z ≤ -1)
Using the standard normal distribution table, we get: P(-1 ≤ z ≤ 1.2) = 0.8849 - 0.1587 = 0.7262. Therefore, the probability that a randomly selected z-score is between -1 and 1.2 is approximately 0.7263, which is the closest option to our answer. The correct option is option D.
To know more about probability refer to:
https://brainly.com/question/27342429
#SPJ11
Find the complete factored form of the
polynomial:
-36a5-24b6
Answers
The factored form of the given polynomial (-36a⁵-24b⁶) is -3 × 12a⁵ + (-2 × 12b⁶).
What are polynomials?A polynomial is a mathematical statement made up of coefficients and indeterminates that uses only the operations addition, subtraction, multiplication, and powers of positive integers of the variables. x² - 4x + 7 is an illustration of a polynomial with a single indeterminate x. They are the cubic polynomial, the zero polynomial, the linear polynomial, and the quadratic polynomial. The degree of polynomials should be a full number. Polynomials are not expressions with negative exponents.So, factor form of -36a⁵-24b⁶:
Now, factorize as follows:
-36a⁵-24b⁶3 × 12a⁵ + 2 × 12b⁶-3 × 12a⁵ + (-2 × 12b⁶) (Get common out)Therefore, the factored form of the given polynomial is -3 × 12a⁵ + (-2 × 12b⁶).
Know more about polynomials here:
https://brainly.com/question/2833285
#SPJ13