If a campaign worker walks 6 kilometers knocking on voters' doors for a candidate before an
election, how many miles did the campaign worker walk?
Answers
Answer with step-by-step explanation:
6 km = 3.72822715 mi
Answer:
Step-by-step explanation:
Thirty three campaign workers called 12,375 eligible voters to encourage them to do their civic duty. Which rate best represents the relationship between the eligible voters reached by each campaign worker?
Related Questions
4. For each babysitting job, Adam charges a fee for his bus fare plus an hourly rate. The graph shows how he calculates the cost of a babysitting job. Write a linear function in the form
y = mx + b to represent the situation.
Ay = 3x+2
B. y = 3x+1
C. y = 6x+2
D. y = -6× + 2
Answers
y = 6x + 2 is the function which Adam charges a rate of $6 per hour and an additional fee of $2 for the bus fare.
The linear function in the form y = mx + b represents the situation where y represents the cost of the babysitting job
x represents the number of hours, "m" represents the hourly rate, and "b" represents the additional fee (bus fare).
y = 3x + 2 represents an hourly rate of 3 and an additional fee of 2.
y = 3x + 1 represents an hourly rate of 3 and an additional fee of 1.
y = 6x + 2 represents an hourly rate of 6 and an additional fee of 2.
y = -6x + 2 represents a negative hourly rate of -6 and an additional fee of 2.
Hence, y = 6x + 2 is the which Adam charges a rate of $6 per hour and an additional fee of $2 for the bus fare.
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
The mean June midday temperature in Desertville is 36°C and the standard deviation is 3°C.Assuming this data is normally distributed, how many days in June would you expect the midday temperature to be between 39°C and 42°C?
Answers
Answer:
The value is \(E(X) = 4 \ days\)
Step-by-step explanation:
From the question we are told that
The mean is \(\mu = 36^oC\)
The standard deviation \(\sigma = 3^oC\)
Generally the probability that in June , the midday temperature is between
39°C and 42°C is mathematically represented as
\(P(39 < X < 42) = P(\frac{39 - 36}{3} < \frac{X - \mu }{\sigma} < (\frac{42 - 36}{3} )\)
\(\frac{X -\mu}{\sigma } = Z (The \ standardized \ value\ of \ X )\)
\(P(39 < X < 42) = P(1 < Z <2 )\)
=> \(P(39 < X < 42) = P(Z < 2) - P( Z <1 )\)
From the z table the area under the normal curve to the left corresponding to 1 and 2 is
P(Z < 2) = 0.97725
and
P(Z < 1) = 0.84134
\(P(39 < X < 42) = 0.97725 - 0.84134\)
=> \(P(39 < X < 42) = 0.13591\)
Generally number of days in June would you expect the midday temperature to be between 39°C and 42°C
\(E(X) = n * P(39 < X 42 )\)
Here n is the number of days in June which is n = 30
\(E(X) = 30 * 0.13591\)
=> \(E(X) = 4 \ days\)
Y is inversely proportional to x, when Y = 7, x = 4.
True or False: the constant of proportionality, k, is 20.
Answers
Answer:
The given statement Y = 7, x = 4 is False.
Step-by-step explanation:
We are given:
Y is inversely proportional to x, when Y = 7, x = 4.
We need to tell if the statement is True or False: the constant of proportionality, k, is 20.
Y is inversely proportional to x
We can write it as: \(y\:\alpha \:\frac{1}{x}\\y=\frac{k}{x}\)
Now, we need to check when Y=7, x = 4 is true or false
We are given k = 20
Now, I can find value of y, by putting values of k and x in the equation:
\(y=\frac{k}{x}\\y=\frac{20}{4}\\y=5\)
When we put x = 4, and k =20, we get Y=5 and not Y=7
So, The given statement Y = 7, x = 4 is False.
please no fake answers ,I need help:)
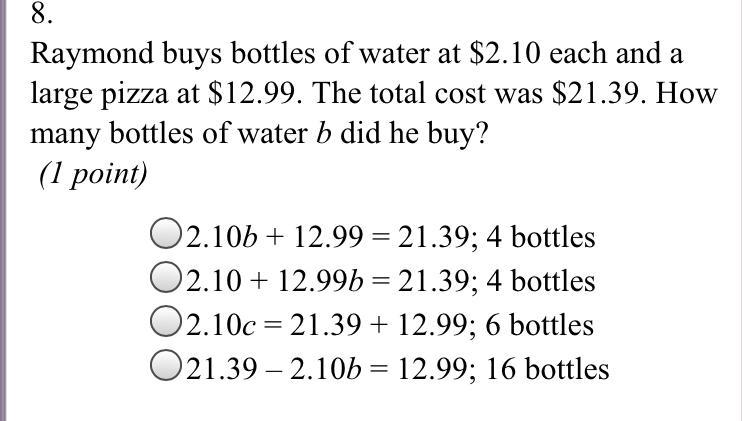
Answers
Answer:
A. 2.10b + 12.99 = 21.39; 4 bottles
Step-by-step explanation:
The b represents bottles of water, at the end of the equation. If each bottle is $2.10, and there were 4 bottles brought, $2.10 * 4 = $8.40, and $8.40 + $12.99 is $21.39.
I need help with all these 5 questions please please help me with these questions





Answers
Answer:
1. (4,5) 2. D 3. J 4.D 5. 64.8 oz
Step-by-step explanation:
math
Is triangle XYZ = ABC ? If so, name the postulate that applies. A. Congruent - ASA B. Congruent - SAS C. Might not be congruent D. Congruent - SSS

Answers
Which equation shows the point-slope form of the line that passes through (3, 2) and has a slope of y plus StartFraction one-half EndFraction equals 3 left-parenthesis x minus 2 right-parenthesis.?
y + 2 =y plus 2 equals StartFraction one-third EndFraction left-parenthesis x plus 3 right-parenthesis.(x + 3)
y – 2 = y minus 2 equals StartFraction one-third EndFraction left-parenthesis x minus 3 right-parenthesis.(x – 3)
y + 3 = y plus 3 equals StartFraction one-third EndFraction left-parenthesis x plus 2 right-parenthesis.(x + 2)
y – 3 = y plus StartFraction one-half EndFraction equals 2 left-parenthesis x minus 3 right-parenthesis.(x – 2)
Answers
The equation that shows the point-slope form of the line passing through (3, 2) with a slope of (1/2) is:
y - 2 = (1/2)(x - 3)
In the point-slope form of a linear equation, the formula is y - y1 = m(x - x1), where (x1, y1) represents a point on the line, and m represents the slope of the line. By substituting the given values into the formula, we can determine the correct equation.
In this case, the given point is (3, 2) and the slope is (1/2). Plugging these values into the formula, we get:
y - 2 = (1/2)(x - 3)
This equation represents the line passing through the point (3, 2) with a slope of (1/2). It is in the point-slope form, which allows us to easily determine the equation of a line based on a given point and slope.
Therefore, the correct equation is y - 2 = (1/2)(x - 3).
For more such answers on Point slope
https://brainly.com/question/29797287
#SPJ8
Answer: B
Step-by-step explanation:
Which equation gives the sum of...
S=0.2/1-8
S=1/8-0.2
S=8/0.2-1
S=8/1-0.2
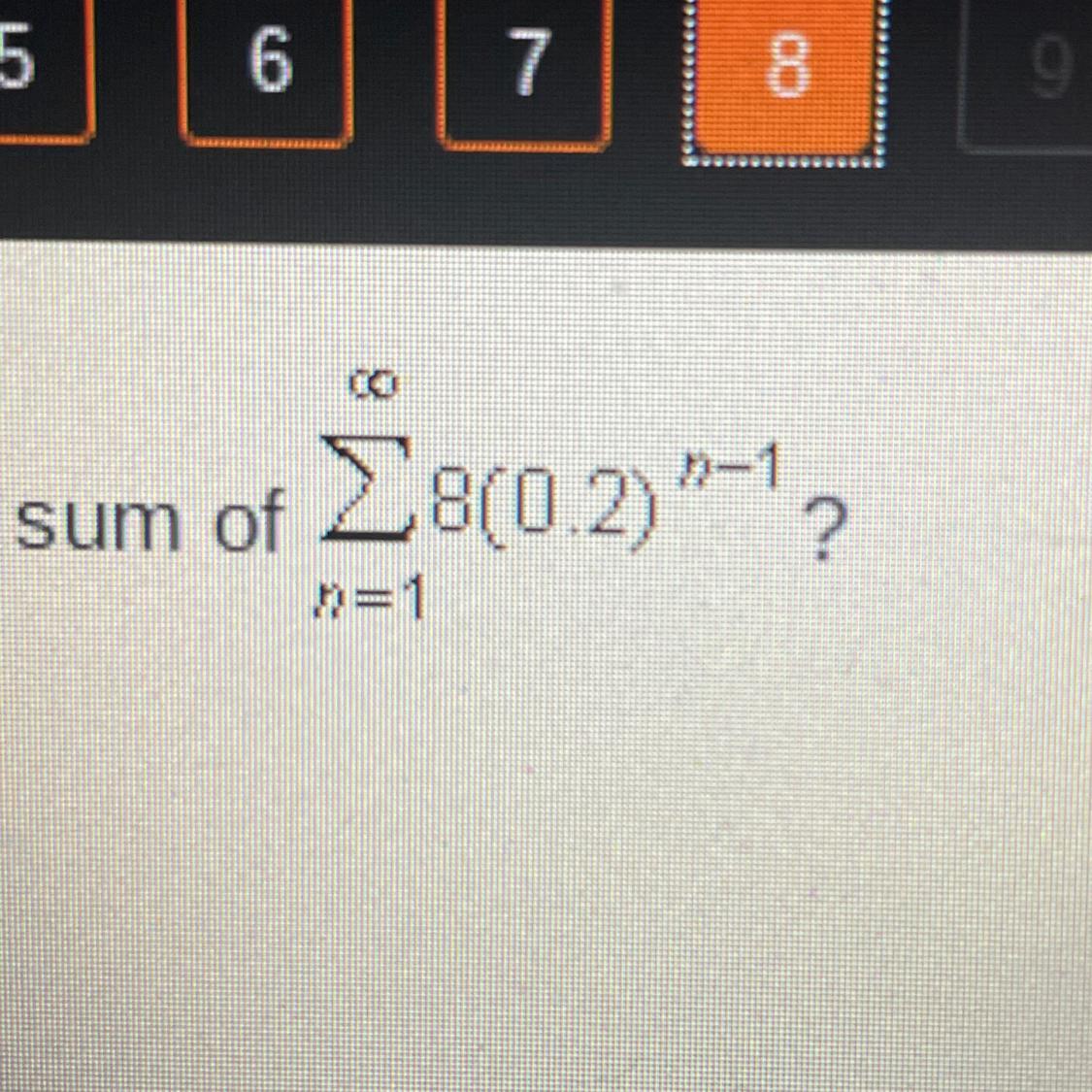
Answers
Answer:
Option D
S=8/1-.2
Step-by-step explanation:
Edg
The sum of the sequence will be S = 8 / (1 – 0.2). Then the correct option is D.
What is the sum of the geometric series?Let a be the first term and r be the common ratio. Then the sum of the geometric series will be
S = a / (1 – r) if r < 1
S = a / (r – 1) if r > 1
The sum of \(\rm \Sigma_{n = 1}^{\infty} 8(0.2)^{n - 1}\).
Then the first term of the geometric sequence will be 8.
And the common difference between the successive terms will be 0.2.
The common ratio less than one, then the formula for the sum will be given as
S = a / (1 – r) if r < 1
Then the sum of the sequence till infinity will be
S = 8 / (1 – 0.2)
S = 8 / 0.8
S = 10
Thus, the sum of the sequence will be S = 8 / (1 – 0.2).
Then the correct option is D.
More about the sum of the geometric series link is given below.
https://brainly.com/question/2771750
#SPJ5
what is 7 plus 56 divided by 4 tims 7
Answers
Answer:
107
Step-by-step explanation:
Answer:
The answer is 105
Step-by-step explanation:
hope its help:)
Adaim has a goal to reach 70 miles. If he hikes 8 miles per day, how long will it take him to hike all 70 miles?
Answers
So basically what you’re going to do is solve for X.
8 times X = 70.
To get X by itself, you divide both sides by 8.
So you have X = 70/8.
Now assuming your teacher prefers a decimal, you’d convert that to 8.75 annnnd because it’s days, you’d round to 9.
Hope this helps!
PLEEEASSEEEEE HELP ME...THIS HAS TO BE TURNED IN 10 MINUTES...WILL GIVE BRAINLIEST..there are two pics plllease help me..THAKYOU!!!


Answers
Answer: I cant see the picture
Step-by-step explanation:
Answer:
lol
no
ask
it teacher of it school
I need help please i will give brainly

Answers
Answer:
C
Step-by-step explanation:
Answer:
C
Step-by-step explanation:
A rectangular pool has a length of 200 ft. You're building a model. Using a scale
factor of 1725, what is the scale length of your model? *
Answers
Answer:
1.4 inches.
Step-by-step explanation:
Given that the length of the pool = 200 ft.
Scale factor = 1725.
As,
\(\text{Scale factor }=\frac{\text{Original length}}{\text{Scaled length}}\)
So,
\(\text{Scaled length} = \frac{\text{Original length}}{\text{Scale factor}}\)
By using the given values, we have
{Scaled length} \(= \frac{200}{1725} ft.=0.116 ft.\)
As 1 foot = 12 inch,
So, scaled length = 0.116 x 12 = 1.4 inches.
Hence, the scale length of the model = 1.4 inches.
7 7/8 - 3 1/4 =? What’s the answer
Answers
Answer:
4 5/8
Step-by-step explanation:
7 7/8= 63/8
3 1/4= 13/4= 26/8
63/8 - 26/8= 37/8
37/8= 4 5/8
Which system of inequalities has the solution setshown in the graph?

Answers
Solution;
The option is the correct answer.
Explanation;
If we combine the two graphs;



My house is 20 miles from yours, but on the map it is only 4 mm away.
What is the scale of the map?
A. 1 mm = 5 mi
B. 1 mm = 20 mi
C. 1 mi= 20 mm
D. 20 mm = 4 mi
E. 5 mi = 4 mm
Answers
Answer:
A. 1mm = 5mi
Step-by-step explanation:
20 mi divided by 4 mm would simplify down to 5 mi per 1mm. If there is 4 mm then there is 5mi*4mm which equals out to 4 mm = 20 mi.
A scale of the map is the relationship between the distance on the map to the actual distance. The scale of the map is 1 mm: 5 miles (ml). Thus the option A is the correct option.
To find out the scale of the map, we have to know about scaling of map.
What is the scaling of map?
The scaling of map is the ratio or relationship between the distance of the map to the original distance.
Given information-
The distance of the two houses on the ground is 20 miles.
The distance of the two houses on the map is 4 mm.
Suppose the scale of the map is \(s\).
As the 20 miles distance on the ground is same as the 4 mm distance on the map.
Thus the scale of the map can be given as,
\(s=\dfrac{4\rm mm}{20\rm miles} \\s=\dfrac{1\rm mm}{5\rm miles}\)
Hence the scale of the map is 1 mm: 5 miles (ml). Thus the option A is the correct option.
Learn more about the scale of map here;
https://brainly.com/question/10283478
Fine the missing length to the nearest 10th

Answers
The value of the missing length to the nearest tenth are;
a. x = 7.5
b. x = 7.8
What is Pythagoras theorem?Pythagoras theorem states that the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse.
Therefore ;
c² = a²+b²
a. x² = 9²-5²
x² = 81-25
x² = 56
x = √56
x = 7.5 ( nearest tenth)
b. using Pythagoras theorem also!
x² = 6²+5²
x² = 36+25
x² = 61
x = √61
x = 7.8( nearest tenth).
Therefore the value of the missing values are 7.5 and 7.8
learn more about Pythagoras theorem from
https://brainly.com/question/343682
#SPJ1
x³ ÷ 3 = y; use x = 3, and y = 1
Answers
Step-by-step explanation:
If x = 3 :
x³ ÷ 3 = y
3³ ÷ 3 = y
27 ÷ 3 = y
y = 27 ÷ 3 = 9
What is the value of x to the nearest hundredth?

Answers
x= 15.45.
Step-by-step explanation:Use the law is sines to find the value of x (check the attached image below).
According to the law, the length of side x is obtained in the following fashion:
\(\frac{14}{sin(65)} =\frac{x}{sin(90)}\\ \\x=\frac{14}{sin(65)}*{sin(90)\)
\(x=15.45\).
Note. We know that the angle infront of side x equals 90 because of the square drawn on the corner where the angle is. Whenever that square is drawn, means that we have a right angle, whose angle is always 90°.

For the function defined here, find f(0), ƒ(2), and f(4) by using the graph below.
x² - 1
f(x) = {¹
-x+1
if
if
x < 2
x > 2
Answers
The values of the functions are f(0) = 2, f(2) = 0 and f(4) = -2
How to evaluate the piece-wise functionThe graph that completes the question is added as an attachment
From the question, we have the following parameters that can be used in our computation:
The graph
On the graph, we can see that the first curve is a quadratic function,
Also, it has an open circle at x = 1
So, we have:
x² + 2 if x < 1
Next, we have a linear equation with a closed circle at x = 1
So we have:
y = -x + 2 for x ≥ 1
This means that
f(0) = 0^2 + 2 = 0f(2) = -2 + 2 = 0f(4) = -4 + 2 = -2Read more about piecewise functions at:
brainly.com/question/3628123
#SPJ1

The width of a rectangular slab of concrete is 14 m less than the length. The area is 32 m². What are dimensions of rectangle? The length of the slab?
Answers
The dimensions of the rectangular slab are 16 meters in length and 2 meters in width.
Let's assume the length of the rectangular slab of concrete is L meters. According to the given information, the width is 14 meters less than the length, so the width would be L - 14 meters.
The formula for the area of a rectangle is A = length × width. In this case, the area is given as 32 m², so we can set up the equation:
32 = L × (L - 14)
Expanding the equation, we get:
32 = L² - 14L
Rearranging the equation, we have:
L² - 14L - 32 = 0
To solve this quadratic equation, we can either factorize it or use the quadratic formula. In this case, it's easier to use the quadratic formula:
L = (-b ± √(b² - 4ac)) / (2a)
Here, a = 1, b = -14, and c = -32. Substituting these values into the formula, we get:
L = (14 ± √((-14)² - 4 × 1 × (-32))) / (2 × 1)
Simplifying further:
L = (14 ± √(196 + 128)) / 2
L = (14 ± √324) / 2
L = (14 ± 18) / 2
Therefore, we have two possible values for L:
L₁ = (14 + 18) / 2 = 16
L₂ = (14 - 18) / 2 = -2
Since the length of the slab cannot be negative, we discard the negative value.
Thus, the length of the rectangular slab is 16 meters. To find the width, we subtract 14 meters from the length:
Width = 16 - 14 = 2 meters
Therefore, the dimensions of the rectangle are 16 meters by 2 meters.
To learn more about dimensions
https://brainly.com/question/31460047
#SPJ8
39÷4=? R ? What is the remainder for 39÷4 all i'm asking for is just the remainder.
Answers
Answer:
3
Step-by-step explanation:
im pretty sure hope this helps
Answer:
9.75
Step-by-step explanation:
9 R 3
Im here to steal ur points (and answer ur question)
Jessamyn bought 3 notebooks that cost $2.25 each and a pen that cost $0.75. Sales tax on her purchases was
6%. What was the amount of the sales tax?
$0.54
$0.75
$0.18
$0.45
Answers

In 1995, the price of a laser printer was 1,299. In 2002, the price of the same type of printer had dropped to 499. Find the percent of decrease
Answers
Answer:
b
Step-by-step explanation:
Sammy wants to spend no more than $35 at the arcade. If he is playing games at the arcade that each cost $0.75, which inequality can be used to find g, the number of games that Sammy can play and stay within his goal
Answers
Answer:
0.75 g ≤ 35
Step-by-step explanation:
if each games costs $0.75, then the answer of g will be given by 35/0.75.
he can go up to exactly $35 but not over
so, the inequality is given by 0.75 g ≤ 35
Given: The height of the cone is 12 mm.12 mm52°Which is closest to the volume of the cone?O 236 mm386 mmO 1,105 mm2,965 mm

Answers
ANSWER:
1105 mm^3
STEP-BY-STEP EXPLANATION:
We have that the volume of the cone has the following formula:
\(V=\frac{1}{3}\cdot\pi\cdot r^2\cdot h\)We do not know the radius of the cone, but we can calculate it since a right triangle is formed, by means of the tangent function we can calculate the value of the radius, just like this:
\(\begin{gathered} \tan \theta=\frac{\text{opposite}}{\text{adjacent}} \\ \text{opposite = 12 mm} \\ \text{adjacent = r} \\ \theta=52\text{\degree} \\ \text{replacing and solving for r} \\ \tan 52=\frac{12}{r} \\ r=\frac{12}{\tan 12} \\ r=9.38\text{ mm} \end{gathered}\)We replace the value of the radius to calculate the value of the volume:
\(\begin{gathered} V=\frac{1}{3}\cdot3.14\cdot9.38^2\cdot12 \\ V=1105.08\cong1105\operatorname{mm} \end{gathered}\)Therefore the volume is equal to 1105 cubic millimeters
What is the relative maximum point for the function shown on the graph?
A)(0, -1)
B)(-3,0)
C(-2,-5)
D)(2,5)
Helpppp plzzz

Answers
Answer:
A) (0, -1)
Step-by-step explanation:
A relative maximum point is a point where the function changes direction from increasing to decreasing (making that point a "peak" in the graph)
(0, -1)
Word Problems : Subtract 18 rupees 9 paise from 75 rupees 80 paise
Write In Step by Step
Answers
Answer:
abb_xdcb_apn come here 10th girls for studies.
Step-by-step explanation:
75.80-18.9
67.71
For each of the following find:
I. lim f (x) as x approaches a from the negative
II. lim f (x) as x approaches a from the positive
III. lim f (x) as x approaches a
a. f(x)={ sin x/3, if x< or equal to pi a=pi
{ x(root3)/(2pi), if x>pi
b. f(x)= (x^2-36)/root(x^2-12x+36) a=6
Answers
Answer:
a. For the function:
f(x) = { sin x/3, if x ≤ π
{ x√3/2π, if x > π
I. To find lim f(x) as x approaches π from the negative side, we need to evaluate f(x) for values of x that are slightly less than π. In this case, since sin(x/3) is a continuous function, we can simply evaluate it at x = π:
lim f(x) as x approaches π- = f(π-) = sin(π/3) = √3/2
II. To find lim f(x) as x approaches π from the positive side, we need to evaluate f(x) for values of x that are slightly greater than π. In this case, we can simply evaluate the other part of the piecewise function at x = π:
lim f(x) as x approaches π+ = f(π+) = π√3/2π = √3/2
III. To find lim f(x) as x approaches π, we need to check whether the left-hand and right-hand limits are equal. In this case, since both the left- and right-hand limits exist and are equal, we have:
lim f(x) as x approaches π = √3/2
b. For the function:
f(x) = (x^2 - 36)/√(x^2 - 12x + 36)
I. To find lim f(x) as x approaches 6 from the negative side, we need to evaluate f(x) for values of x that are slightly less than 6. In this case, we can substitute x = 6 - h, where h is a positive number approaching zero, to get:
lim f(x) as x approaches 6- = lim f(6 - h) as h approaches 0
Substituting x = 6 - h into the function, we get:
f(6 - h) = [(6 - h)^2 - 36]/√[(6 - h)^2 - 12(6 - h) + 36]
= [h^2 - 12h]/√[h^2]
Simplifying the numerator and denominator separately, we get:
f(6 - h) = h(h - 12)/|h|
Since h approaches 0 from the positive side, we have:
lim f(6 - h) as h approaches 0+ = lim h(h - 12)/h as h approaches 0+ = lim (h - 12) as h approaches 0+ = -12
II. To find lim f(x) as x approaches 6 from the positive side, we need to evaluate f(x) for values of x that are slightly greater than 6. In this case, we can substitute x = 6 + h, where h is a positive number approaching zero, to get:
lim f(x) as x approaches 6+ = lim f(6 + h) as h approaches 0
Substituting x = 6 + h into the function, we get:
f(6 + h) = [(6 + h)^2 - 36]/√[(6 + h)^2 - 12(6 + h) + 36]
= [h^2 + 12h]/√[h^2]
Simplifying the numerator and denominator separately, we get:
f(6 + h) = h(h + 12)/|h|
Since h approaches 0 from the positive side, we have:
lim f(6 + h) as h approaches 0+ = lim h(h +
Step-by-step explanation:
identify the special product by writing the letter of the answer on the space provided ( question in photo number 1 )

Answers
Question:
Solution:
Note that :
\(x^2+9x\text{ + 20 = 1(x+4)(x+5)}\)where the left hand of the equation represents a trinomial and the right hand of the equation represents a product of two binomials. Then, we can conclude that the correct answer is:
B
