If 64 is added to a number, the result is 40 less than three times the number. Find the number.
Answers
Answer: 52
Step-by-step explanation:
\((x+64)+40=3x\\x+64+40=3x\\x+104=3x\\104=2x\\ 52=x\)
Checking my work:
\(52*3=156\\\\52+64=116\\116+40= 156\)
Related Questions
S={(3,p),(3,0),(4,q),(1,4)}
Answers
Answer:
S = {(3,p), (3,0), (4,q), (1,4)} is a set of ordered pairs, where the first element of each ordered pair is an integer and the second element is a variable. The set consists of four ordered pairs:
(3,p): The first element is 3 and the second element is p.
(3,0): The first element is 3 and the second element is 0.
(4,q): The first element is 4 and the second element is q.
(1,4): The first element is 1 and the second element is 4.
Please help me in confused

Answers
Answer:
20\(c^{6}\)
Step-by-step explanation:
using the rule of exponents
\(a^{m}\) × \(a^{n}\) = \(a^{(m+n)}\)
given
(- 4c³)(- 5c³) ← remove parenthesis
= - 4 × c³ × - 5 × c³
= - 4 × - 5 × c³ × c³
= 20 × \(c^{(3+3)}\)
= 20\(c^{6}\)
Is the square root of 85 a rational number
Answers
Since 85 is not a perfect square, it is an irrational number. This means that the answer to "the square root of 85?" will have an infinite number of decimals.
Write the equation of the line in fully simplified slope-intercept form

Answers
Answer:
y=-5x-5
Step-by-step explanation:
The line contains points at (-2,5) and (0,-5)
(y1-y2) / (x1-x2) = slope
(-2,5) =(x1,y1)
(0,-5) = (x2,y2)
(5--5) / (-2-0)
10 / -2 = -5
y= -5x + b
plug in points for x and y to find b
5=-5(-2)+b
5=10+b
-5=b
y=-5x-5
please help me answer this question thank you

Answers
Answer:
A
Step-by-step explanation:
Of the students in the photography club, 15% are not planning to go to the art show. There are 6 students not going to the art show. How many students are in the photography club? Use any strategy to solve.
Answers
Answer:
There are 40 students in the photography club.
Step-by-step explanation:
Given that:
Percent of people not going to art show = 15%
Number of people not going to art show = 6
Let,
x be the number of students in the photography club
15% of x = 6
\(\frac{15}{100}x=6\)
0.15x = 6
Dividing both sides by 0.15
\(\frac{0.15x}{0.15}=\frac{6}{0.15}\\x= 40\)
Hence,
There are 40 students in the photography club.
a food server at harpers restaurant earns 5 dollars plus a 15% tip on the money made on each table he serves. Sam worked as a food server for six hours last friday and his tables earned $600. How much money did Sam make that day?
Answers
Answer:
The answer is given in the picture
Step-by-step explanation:
Do you remember me calista
I am alvena

Answer:
$70
Step-by-step explanation:
$5 x 6 hours = $30
$600 ÷ 15% = $40
$30 + $40 = $70
when a slice of buttered toast is accidentally pushed over the edge of a counter, it rotates as it falls. suppose the distance to the floor is 82 cm and the toast rotates less than 1 rev.
Answers
(i) The smallest angular speeds that cause the toast to hit and then topple to be butter-side down 3.84 rad / s
(ii) The largest angular speeds that cause the toast to hit and then topple to be butter-side down 11.51 rad / 5
The distance from the counter to the floor, d = 82 cm = 0.82 m
Rotation is less than 1 rev.
The toast rotates at a constant angular speed as it falls, and the toast is falling with a constant acceleration (gravitational acceleration).
Using the kinematic equations of motion to calculate the time taken by the toast to hit the floor
\($d & =v_i t+\frac{1}{2} g t^2 \\\)
\($d & =0+\frac{1}{2} g t^2 \\\)
Therefore \($t & =\sqrt{\frac{2 d}{g}}=\sqrt{\frac{2 \times 0. 82}{9.8}\)
= 0.409 s
Where
\($v_i$\) is the initial speed of the toast, \($v_i=0$\) because the toast is falling from rest.
t the time that the toast takes to hit the floor.
g is the gravitational acceleration.
d is the distance between the counter and the floor.
Part (a)The toast is accidentally pushed over the edge of the counter with the butter side up, then the toast rotates as it falls. If the toast hits the ground and then topples to be butter-side down, it has to land on one of its edges. The smallest angle, in this case, is \($\frac{1}{4}$\) revolution and corresponds to the smallest angular speed
\($\omega_{\min } & =\frac{\Delta \theta}{\Delta t} \\\)
\($\omega_{\min } & =\frac{0.25 \mathrm{rev}}{\Delta t}=\frac{0.25 \times 2 \pi}{\Delta t} \\\)
Therefore \($ \omega_{\min } & =\frac{0.5 \pi}{0.409}\)
= 3.84 rad/s
Where
\($\omega_{\min }$\) is the minimum angular speed for the toast to land butter-side down. \($\Delta \theta$\) is the smallest angle for the toast to land butter-side down in radians.
\($\omega_{\min }$\) = 3.84 rad / s
Part b:
The toast is accidentally pushed over the edge of the counter with the butter side up, then the toast rotates as it falls. If the toast hits the ground and then topples to be butter-side down, it has to land on one of its edges. The largest angle, in this case, is \($\frac{3}{4}$\) revolution and corresponds to the largest angular speed
\($\omega_{\max } & =\frac{\Delta \theta}{\Delta t} \\\)
\($\omega_{\max } & =\frac{0.75 \mathrm{rev}}{\Delta t}=\frac{0.75 \times 2 \pi}{\Delta t} \\\)
Therefore \($ \omega_{\max } & =\frac{1.5 \pi}{0.409}\)
= 11.51 rad / s
For more questions on angular speed
https://brainly.com/question/13785503
#SPJ4
When a slice of buttered toast is accidentally pushed over the edge of a counter, it rotates as it falls. If the distance to the floor is 82 cm and for rotation less than 1 rev, what are the (i) smallest and (ii) largest angular speeds that cause the toast to hit and then topple to be butter-side down?
A pentagon is formed by connecting the tips of a starfish's leds, as shown below
what is the area of the Pentagon.

Answers
Answer:
71.5
Step-by-step explanation:
You have to break it down into 3 different triangles. The area formula for a triangle is A = 1/2 * b * h.
Triangle 1: A = 1/2 * 10 * 4 = 20
Triangle 2: A = 1/2 * 11 * 5 = 27.5
Triangle 3: A = 1/2 * 6 * 8 = 24
Now add all your totals together, 20+27.5+24 = 71.5
K
J
L
5
M
Given that the rectangle above has a perimeter of 34 units, find mZKLJ. Round the answer to the nearest hundredth.
A. 8.46°
B. 22.62⁰
C. 24.62°
D. 65.38°
Answers
The measure of angle ZKLJ is approximately is 24.62°. Option C is right choice.
To find the measure of angle ZKLJ in the given rectangle:
Since a rectangle has opposite sides equal in length, we can divide the perimeter of 34 units by 4 to find the length of each side:
34 units / 4 = 8.5 units
Now, consider triangle ZKL. We know that ZK = 8.5 units and KL = 5 units.
Using the Pythagorean theorem, we can calculate the length of ZL:
\(ZL^2\) = \(ZK^2 + KL^2\)
\(ZL^2\) = \((8.5 \:units)^2 + (5 \:units)^2\)
\(ZL^2\) = 72.25 + 25
\(ZL^2\) = 97.25
ZL ≈ 9.86 units
Now, let's calculate the tangent of angle ZKL:
tan(ZKL) = KL / ZL
tan(ZKL) = 5 units / 9.86 units
tan(ZKL) ≈ 0.507
Using the inverse tangent (arctan) function, we can find the measure of angle ZKLJ:
ZKLJ ≈ arctan(0.507)
ZKLJ ≈ 27.46°
Therefore, rounding to the nearest hundredth, the measure of angle ZKLJ is approximately 27.46°.
The closest option to this answer is option C: 24.62°.
For such more questions on measure of angle
https://brainly.com/question/25716982
#SPJ11
Question-
Given that the rectangle above has a perimeter of 34 units, find mZKLJ. Round the answer to the nearest hundredth.
A. 8.46°
B. 22.62⁰
C. 24.62°
D. 65.38°

What number is represented by point B?
4/5
1 4/5
1 5/4
2 1/5
Answers
Answer:
1 5/4
Step-by-step explanation:
Find the value of x such that the line containing (1,2) and (5,3) is perpendicular to the line containing (x,4) and (3,0)
Answers
The value of x that makes the line containing (1,2) and (5,3) perpendicular to the line containing (x,4) and (3,0) is x = 2.
To determine the value of x such that the line containing (1,2) and (5,3) is perpendicular to the line containing (x,4) and (3,0), we need to find the slope of both lines and apply the concept of perpendicular lines.
The slope of a line can be found using the formula:
slope = (change in y) / (change in x)
For the line containing (1,2) and (5,3), the slope is:
slope1 = (3 - 2) / (5 - 1) = 1 / 4
To find the slope of the line containing (x,4) and (3,0), we use the same formula:
slope2 = (0 - 4) / (3 - x) = -4 / (3 - x)
Perpendicular lines have slopes that are negative reciprocals of each other. In other words, if the slope of one line is m, then the slope of a line perpendicular to it is -1/m.
So, we can set up the equation:
-1 / (1/4) = -4 / (3 - x)
Simplifying this equation:
-4 = -4 / (3 - x)
To remove the fraction, we can multiply both sides by (3 - x):
-4(3 - x) = -4
Expanding and simplifying:
-12 + 4x = -4
Adding 12 to both sides:
4x = 8
Dividing both sides by 4:
x = 2
For more such questions on line.
https://brainly.com/question/280216
#SPJ8
Line s has a slope of 8/5. Line t had a slope of 8/3. Are line s and t parallel or perpendicular?
Answers
The lines are neither parallel nor perpendicular.
Define slope.
Slope, usually referred to as rise over run, is the "steepness" of the line. By dividing the difference in y values between two points by the difference in x values, we may determine slope. The ratio of the increase in elevation between two points to the run in elevation between those same two points is referred to as the slope. In other words, the line's slope reveals how quickly y changes in relation to x. When the slope is 2, y changes twice as quickly as x; when the slope is 1/2, y changes half as quickly as x; and so on.
Given,
Line s has a slope of 8/5. Line t had a slope of 8/3.
The lines are neither parallel nor perpendicular.
To learn more about slope, visit:
https://brainly.com/question/3605446
#SPJ13
This figure shows two similar polygons; DEFG∼TUVS. Find the value of x.
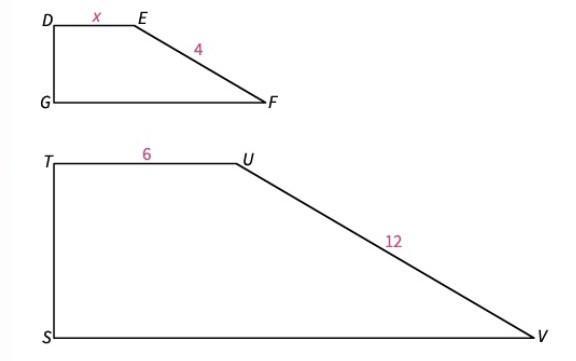
Answers
According to the question, both polygons are similar. It means you can use proportions to find the value of x.
\(\frac{DE}{TU}=\frac{EF}{UV}\)Replace for the given values in the picture
\(\begin{gathered} \frac{x}{6}=\frac{4}{12} \\ x=\frac{4}{12}\cdot6 \\ x=2 \end{gathered}\)x has a value of 2.
The failure of a component cannot be observed directly, and a sensor is designed to a detect the failure. Statistical data indicate that the probability of failure of the component is 0.1%. When the component fails, an alarm, which indicates a failure, is activated by the sensor 99% of the time. When the component does not fail, the sensor activates an alarm 2% of the time. (a) What is the probability that the alarm is activated? (b) If the alarm is activated, determine the probability that the component actually failed.
Answers
a) The probability that the alarm is activated is approximately 0.021
b) The probability that the component actually failed given that the alarm is activated is approximately 0.047
(a) To calculate the probability that the alarm is activated, we can use the law of total probability, which states that the probability of an event can be calculated by summing the probabilities of all possible ways that the event can occur. Using the probabilities given in the problem, we have:
P(alarm is activated) = P(component fails and alarm is activated) + P(component does not fail and alarm is activated)
= P(component fails) × P(alarm is activated given component fails) + P(component does not fail) × P(alarm is activated given component does not fail)
= 0.001 × 0.99 + 0.999 × 0.02
= 0.02097
Therefore, the probability is 0.021
(b) To determine the probability that the component actually failed given that the alarm is activated, we can use Bayes' theorem, which relates the conditional probabilities of two events. Specifically, we want to calculate the probability of the component failing given that the alarm is activated, which can be written as:
P(component fails | alarm is activated) = P(alarm is activated | component fails) × P(component fails) / P(alarm is activated)
We already know the values of P(alarm is activated | component fails) and P(component fails) from part (a). To calculate P(alarm is activated), we can use the law of total probability as before:
P(alarm is activated) = P(component fails) × P(alarm is activated given component fails) + P(component does not fail) × P(alarm is activated given component does not fail)
= 0.001 × 0.99 + 0.999 × 0.02
= 0.02097
Substituting all the values into Bayes' theorem, we get:
P(component fails | alarm is activated) = 0.99 × 0.001 / 0.02097
≈ 0.047
Therefore, the probability is 0.047
Learn more about probability here
brainly.com/question/11234923
#SPJ4
Use the Laws of logarithms to rewrite the expression

Answers
The expression log₃(x²∛y²) using the laws of logarithms is 2log₃(x) + 2/3log₃(y)
Rewriting the expression using the laws of logarithmsFrom the question, we have the following parameters that can be used in our computation:
log₃(x²∛y²)
The product law of logarithms states that
log(ab) = log(a) + log(b)
Using the above as a guide, we have the following:
log₃(x²∛y²) = log₃(x²) + log₃(∛y²)
The power law of logarithms states that
log(aᵇ) = blog(a)
Using the above as a guide, we have the following:
log₃(x²∛y²) = 2log₃(x) + 2/3log₃(y)
This means that the values of A and B are A = 2 and B = 2/3
Read more about logarithms at
https://brainly.com/question/28041634
#SPJ1
how do u graph the solution y=2x-1 iready
Answers
Answer:
Step-by-step explanation:
y=mx+b
m= slope and b= y intercept
you'll start with a point on the y axis on -1
and the slope will go up so towards the right corner up but 2/1 points
A quantitative data set has size 60. At least how many observations lie within six standard deviations to either side of the mean? At least nothing observations lie within six standard deviations to either side of the mean. (Round up to the nearest whole number.)
Answers
Answer:
,,
Step-by-step explanation:
Which division sentence is related to the product of a/3(a/3) when a≠0
Answers
Answer:
\(\frac{a}{3} \frac{.}{.}\frac{3}{a} =1\)
Step-by-step explanation:
As we seen that the reciprocal of the a/3(a/3) provides the result as a product number that gives the output as 1 .
Also we know that two fractions number gives output 1 if they are the reciprocal or multiplicative inverse from each other.
So, a/3(a/3
\(\frac{3a}{3a} \\\\it\ can\ be \ written \ as \\\frac{3}{a} \frac{.}{.}\frac{a}{3}=\ 1\)
Answer:
It is not D!!!
Step-by-step explanation:
Order:3/4 strength isomil 4 oz p.o .q4h for 24 hours. How many mls of water will you add to ensure 4 oz of3/4 strength
Answers
To ensure 4 ounces of 3/4 strength isomil, we would add approximately 118.28 milliliters of water to 3 ounces of isomil powder.
To ensure 4 ounces of 3/4 strength isomil, we need to calculate the amount of isomil powder and water needed.
First, we need to determine the amount of isomil powder required. Since the strength is 3/4, we only need 3/4 of the total volume to be isomil. In this case, the total volume is 4 ounces, so 3/4 of 4 ounces is \((3/4) \times 4 = 3\)ounces of isomil powder.
Next, we need to determine the amount of water needed. Since the total volume is 4 ounces and we already have 3 ounces of isomil powder, the remaining 1 ounce needs to be water.
To convert ounces to milliliters, we need to know the conversion rate. In general, 1 ounce is approximately equal to 29.57 milliliters. Therefore, 4 ounces is approximately equal to \(4 \times 29.57 = 118.28 milliliters.\)
For more such questions on strength
https://brainly.com/question/27933827
#SPJ8
the current in the electronic circuit in the mobile phone was 0.12a the potential difference across the battery was 3.9V. calculate the resistance of the electronic circuit in the mobile phone
Answers
Answer:
Step-by-step explanation:
V = 3.9V
I = 0.12A
Ohm's Law, V = IR
Rearranging Ohm's Law, R = V/I
R = 3.9/0.12 = 32.5Ω
Given h(x) = -5x + 3, find h(5).
Answers
Answer:
h(5) = -22
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
Brackets Parenthesis Exponents Multiplication Division Addition Subtraction Left to RightAlgebra I
Function NotationStep-by-step explanation:
Step 1: Define
h(x) = -5x + 3
h(5) is x = 5
Step 2: Evaluate
Substitute in x [Function]: h(5) = -5(5) + 3Multiply: h(5) = -25 + 3Add: h(5) = -22Determine the margin of error for the confidence interval for the mean:63< <97

Answers
To determine the margin of error, subtract the less value of the confidence interval to the greater value:
\(97-63=34\)Now, divide it by 2:
\(\frac{34}{2}=17\)Thus, the margin of error for the confidence interval for the mean is 17.
To the nearest whole number,
which is the best estimate?
45.29+63.92+4.02 (29.92
A.198
B.229
C.254
D.3390
Answers
Answer:
B. 229
Step-by-step explanation:
I solved it by multiplying the 4.02 and 29.92. Then, added the numbers together and rounding the solution to the nearest whole number.
Frank had four different credit cards, the balances and interest information of which are outlined in the table below. If Frank budgets to pay off all four credit cards in 24 months, what will his total monthly credit card payment be?

Answers
Answer:
D
Step-by-step explanation:
I got this problem too and I got it correct
Answer:
✅ D. $462.91i took the test⬇️

Find the surface area of the prism 12in 4 in 3in 5in 5in 6in

Answers
Answer:
Area of trapezoid:
12 + 6<-- your two bases of the trapezoid = 18
18 x 4 = 72, 72 divided by 2 = 36
now we multiply by 2 since there are 2 trapezoids:
36 x 2 = 72
Area of rectangle in front:
6 x 3 = 18
Area of the 2 rectangles on the sides:
5 x 3 = 15
(multiply by 2 since there are two rectangles on both sides)
15 x 2 = 30
Area of rectangle on the back:
12 x 3 = 36
Now lets add up all the areas:
72 + 18 + 30 + 36 = 156 in2 is your answer.
What is the value of x?
Enter
your answer in the box.

Answers
Answer:
x = 6
Step-by-step explanation:
Triangle BCD: cos(60) = x/BC => BC = x/cos(60)
Triangle ABC: sin(45) = BC/6√2 => BC = (6√2)sin(45)
so x/cos(60) = (6√2)sin(45)
x/(1/2) = (6√2)(√2/4)
x/2 = 12/4
x = 2(3)
x = 6
Tell whether the given side lengths can represent the sides of a right triangle
10, 12, 20
Determine if the segment lengths form an acute, right, or obtuse triangle,
10, 11, 14
26.
Need help with all of these please need this asap. Please show work

Answers
23. By the diagram, the triangle is a \(45^\circ - 45^\circ-90^\circ\) triangle. Therefore, the triangle is isosceles, so \(x=6.\) And by the Pythagorean theorem, \(y^2=x^2+6^2=6^2+6^2=72,\) and taking the square root yields \(y = 6\sqrt{2}.\)
24. Notice that by the diagram, the triangle is a \(30^\circ-60^\circ-90^\circ\) triangle. It is well known that in these special types of triangles, if \(a\) is the side length opposite the \(30^\circ\) angle, then the side length opposite the \(90^\circ\) angle is \(2a,\) and finally the side length opposite the \(60^\circ\) is \(a\sqrt{3}.\) This is shown in the image I've attached below, and can also be easily proven by the fact that two of these triangles combine to form an equilateral triangle.
So using this fact, we know that \(x = \frac{8}{2} = 4,\) and \(y = x\sqrt{3} = 4\sqrt{3}.\)
25. Tell whether the given side lengths can represent the sides of a right triangle: 10, 12, 20
For this question, we simply use the converse of the Pythagorean theorem. One part of its statement says that if a triangle has sides of length \(a, b, c\) such that \(a^2 + b^2 = c^2\), and \(c\) is the longest side, then the angle opposite the side of length \(c\) is a right angle.
Thus, if the triple \((a, b, c)\) does not satisfy the equation, the triangle it forms is not a right triangle. In our case, the corresponding values for \((a, b, c)\) are \((10, 12, 20),\) because \(20\) is the largest number in this triple. But \(10^2+12^2=244\neq 400 = 20^2,\) so the triangle with side lengths \(10, 12, 20\) is not a right triangle.
26. Another statement of the converse of the Pythagorean theorem is that if a triangle has side lengths \(a, b, c\) such that \(c^2 > a^2+b^2\) , with \(c\) being the longest side, then the triangle is an obtuse triangle. So the corresponding values for \(a, b, c\) are \(10, 11, 14,\) and because \(14^2 = 196 < 221 = 10^2+11^2,\) the triangle is an obtuse triangle.


What values of b satisfy 3(2b + 3)² = 36?
Answers
Answer:
The values of b that satisfy the equation are:
b = (2√3 - 3) / 2
b = (-2√3 - 3) / 2
In other words, b can take the values (2√3 - 3) / 2 or (-2√3 - 3) / 2.
Step-by-step explanation:
To find the values of b that satisfy the equation 3(2b + 3)² = 36, we can solve for b by following these steps:
1. Divide both sides of the equation by 3:
(2b + 3)² = 12
2. Take the square root of both sides:
√[(2b + 3)²] = √12
Simplifying further:
2b + 3 = ±√12
3. Subtract 3 from both sides:
2b = ±√12 - 3
4. Divide both sides by 2:
b = (±√12 - 3) / 2
Simplifying further:
b = (±√4 * √3 - 3) / 2
b = (±2√3 - 3) / 2
Therefore, the values of b that satisfy the equation are:
b = (2√3 - 3) / 2
b = (-2√3 - 3) / 2
In other words, b can take the values (2√3 - 3) / 2 or (-2√3 - 3) / 2.
Solve the problem.
A landscaping team plans to build a rectangular garden that is between 240 yd² and 360 yd2 in area. For aesthetic reasons, they also want the
length to be 1.2 times the width. Determine the restrictions on the width so that the dimensions of the garden will meet the required area. Give exact
values and the approximated values to the nearest tenth of a yard.
Answers
The restrictions on the width is that it must be between 14.1 yards and 17.3 yards
How to determine the restrictions on the widthFrom the question, we have the following parameters that can be used in our computation:
Area = between 240 yd² and 360 yd²
Also, we have
Length = 1.2 times the width
This means that
l = 1.2w
The area is then calculated as
Area = lw
So, we have
Area = 1.2w²
This means that
240 < 1.2w² < 360
Divide through by 1.2
200 < w² < 300
Take the square roots
14.14 < w < 17.32
Approximate
14.1 < w < 17.3
Hence, the width must be between 14.1 yards and 17.3 yards
Read more about areas at
https://brainly.com/question/25292087
#SPJ1