If 2/3=x/12, what is the vaule of x? a 4 b 8 c 18 d 24
Answers
Answer:
b.8
Step-by-step explanation:
2/3 = x/12
8/12 = x/12
x = 8
Related Questions
Assume that the duration of human pregnancies can be described by a Normal model with mean days and standard deviation days.
a) What percentage of pregnancies should last between and days?
b) At least how many days should the longest % of all pregnancies last?
c) Suppose a certain obstetrician is currently providing prenatal care to pregnant women. Let represent the mean length of their pregnancies. According to the Central Limit Theorem, what's the distribution of this sample mean, ? Specify the model, mean, and standard deviation.
d) What's the probability that the mean duration of these patients' pregnancies will be less than days?
Answers
Using the normal distribution, it is found that:
a) The percentage of pregnancies lasting between 265 and 275 days is of 20.52%.
b) The longest 25% of the pregnancies last at least 276 days.
c) The distribution is approximately normal, with mean of 264 days and the standard deviation of 2.85 days.
d) The probability that the mean is less than 267 days is of 0.8531 = 85.31%.
Normal Probability DistributionThe z-score of a measure X of a variable that has mean symbolized by \(\mu\) and standard deviation symbolized by \(\sigma\) is given by the rule presented as follows:
\(Z = \frac{X - \mu}{\sigma}\)
The z-score represents how many standard deviations the measure X is above or below the mean of the distribution, depending if the calculated z-score is positive or negative.Using the z-score table, the p-value associated with the calculated z-score is found, and it represents the percentile of the measure X in the distribution.By the Central Limit Theorem, the sampling distribution of sample means of size n has standard deviation \(s = \frac{\sigma}{\sqrt{n}}\). The distribution is normal and the mean remains constant.The mean and the standard deviation of pregnancy lengths are given, respectively, by:
\(\mu = 264, \sigma = 18\)
The proportion between 265 and 275 is the p-value of Z when X = 275 subtracted by the p-value of Z when X = 265, hence:
X = 275:
\(Z = \frac{X - \mu}{\sigma}\)
Z = (275 - 264)/18
Z = 0.61
Z = 0.61 has a p-value of 0.7291.
X = 265:
\(Z = \frac{X - \mu}{\sigma}\)
Z = (265 - 264)/18
Z = 0.06
Z = 0.06 has a p-value of 0.5239.
0.7291 - 0.5239 = 0.2052 = 20.52% is the percentage.
The longest 25% of pregnancies last at least the 75th percentile, which is X when Z = 0.675, hence:
\(Z = \frac{X - \mu}{\sigma}\)
0.675 = (X - 264)/18
X - 264 = 0.675 x 18
X = 276 days.
For the sample of 40 women, the standard deviation is given as follows:
\(s = \frac{18}{\sqrt{40}} = 2.85\)
For item d, the probability is the p-value of Z when X = 267, hence:
\(Z = \frac{X - \mu}{\sigma}\)
By the Central Limit Theorem
\(Z = \frac{X - \mu}{s}\)
\(Z = \frac{267 - 264}{2.85}\)
Z = 1.05
Z = 1.05 has a p-value of 0.8531.
Missing InformationAssume that the duration of human pregnancies can be described by a normal model with a mean 264 days and a standard deviation 18 days.
a) What percentage of pregnancies should last between 265 and 275 days?
b) At least how many days should the longest 25% of all pregnancies last?
P(X> ___) =.25
c) Suppose a certain obstetrician is currently providing prenatal care to 40 pregnant women.Let y represent the mean length of their pregnancies. According to the central limit theorem, what is the mean and standard deviation SD(y) of the normal model of the distribution of the sample mean, y?
Mean =
SD(y)=
d) What is the probability that the mean duration of these patients' pregnancies will be less than 267 days?
P(y<276)=
More can be learned about the normal distribution at https://brainly.com/question/25800303
#SPJ1
NEED HELP!! I"LL GIVE YOU BRAINLIEST!! Find the value of b. a = 3 and c =12

Answers
Answer: b = 11.62
Step-by-step explanation:
We can use this formula to solve for b:
\(b^{2} =\) \(\sqrt{c^{2}-a^{2} }\)
\(b^{2} =\) \(\sqrt{12^{2}-3^2 }\)
\(b^2= \sqrt{144-9}\)
= 11.61895004
We can round that to 11.62.
Hope this helped!
Find the slope of identity function using points (0,0) and ( 3,3) then from two points (0,0) and (-3,-3). Is there any change in its slope?

Answers
There is no change in its slope as initial and final slope is 1.
What is slope?
In arithmetic, the slope or gradient of a line may be a variety that describes each the direction and therefore the abruptness of the line.
Main body:
formula for slope with two points form is =
y -y₁ =( y₂-y₁ /x₂-x₁ )(x - x₁)
according to question ,
points are (0,0) and (3,3)
y - 0 = (3-0/3-0)(x -0)
y = 3/3 *x
y = x
hence slope of line is 1.
Now points are (0,0) and (-3,-3).
y - 0 = (-3-0/-3-0)(x -0)
y =- 3/-3 *x
y = x
hence slope of line is 1.
So there is no change in its slope.
To know more about slope , visit:
https://brainly.com/question/3493733
#SPJ1
See attached Screenshot

Answers
The expression ∛(t⁴m²) / (m³t) in the simplified form will be written as \(\rm \frac{t^{1/3}}{m^{7/3}}\).
What is Algebra?Algebra is the study of abstract symbols, while logic is the manipulation of all those ideas.
The acronym PEMDAS stands for Parenthesis, Exponent, Multiplication, Division, Addition, and Subtraction. This approach is used to answer the problem correctly and completely.
The expression is given below.
⇒ ∛(t⁴m²) / (m³t)
Simplify the expression, then we have
⇒ ∛(t⁴m²) / (m³t)
⇒ t∛(tm²) / (m³t)
⇒ ∛(tm²) / (m³)
Simplify the equation further, then we have
\(\rm \rightarrow \dfrac{\sqrt[3]{\rm tm^2} }{m^3}\\\\\rightarrow \dfrac{t^{1/3}m^{2/3}}{m^3}\\\\\rightarrow \dfrac{t^{1/3}}{m^{7/3}}\)
The expression ∛(t⁴m²) / (m³t) in the simplified form will be written as \(\rm \frac{t^{1/3}}{m^{7/3}}\).
More about the Algebra link is given below.
https://brainly.com/question/953809
#SPJ1
You are given the great circle of a sphere is a length of 25 miles. What is the volume of the sphere
Answers
The volume of the sphere is approximately 3431.82 cubic miles.
To find the volume of a sphere, we need the radius of the sphere. The length of a great circle is the circumference of the sphere, which is related to the radius by the formula C = 2πr, where C is the circumference and r is the radius.
In this case, we are given that the length of the great circle is 60 miles. We can use this information to find the radius of the sphere.
C = 2πr
60 = 2πr
Divide both sides of the equation by 2π:
r = 60 / (2π)
r = 30 / π
Now that we have the radius, we can use the formula for the volume of a sphere:
V = (4/3)πr³
V = (4/3)π(30/π)³
V = (4/3)π(27000/π³)
V = (4/3)π(27000/π³)
V = (4/3)π(27000/π³)
V = (4/3)(27000/π²)
V = (4/3)(27000/9.87) (approximating π to 3.14)
V ≈ 3431.82 cubic miles
Therefore, the volume of the sphere is approximately 3431.82 cubic miles.
for such more question on volume
https://brainly.com/question/6204273
#SPJ8
Question
You are given the great circle of a sphere is a length of 60 miles. What is the volume of the sphere?
Urgent!! Find the length of B by using the Pythagorean Theorem

Answers
Answer:
Step-by-step explanation:
24^2 + b^2 = 40^2
576 + b^2 = 1600
b^2 = 1024
b = 32
32
Step-by-step explanation:
\( {a}^{2} + {b}^{2} = {c}^{2} \)
a= 24 , b= b , c=40
In order to find b, you have to change the equation a bit. Your new equation will look like \( {c}^{2} - {a}^{2} = {b}^{2} \)
here is the step by step now
\( {40}^{2} - {24}^{2} = {b}^{2} \)
\( {1600} - {576} = {b}^{2} \)
\( {1024} = {b}^{2} \)
**now you need to take the square root of both sides and you get 32**
solve for x !
\(x {}^{2} - 36 = 0\)
thankyou ~
Answers
Answer:
X = 6. Give brainliest
Step-by-step explanation:
Solution:
x² - 36 = 0
or x² = 36
or x² = 6²
Therefore, the value of x is 6.
Answer:
x^2-36=0
x^2-36+36=0+36
x^2=36
x=√(36),x=-√(36)
√(36) → 6
-√(36) → -6
x=6,x=-6
Write an equation of the line using function notation.
Slope 0; through (−3,−2)
The equation of the line is f(x)=
Answers
The equation of the line having slope 0 and passing through (-3,-2) is f(x) = -2.
Any horizontal line has the same y-value for every point on the line. We are given that the line passes through the point (-3,-2). This means that f(-3) = -2, since the y-value of the point (-3,-2) corresponds to the value of the function at x = -3.
This is because no matter what x-value we plug into the function, the output (y-value) will always be -2. Therefore, the equation of the line in function notation is f(x) = -2.
To know more about equation of line, visit,
https://brainly.com/question/18831322
#SPJ1
What is the total surface area of the prism?
82 sq. cm
12 sq. cm
94 sq. cm
HEPLP WLL MAR BRANLEST
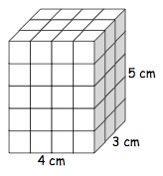
Answers
Answer:
12 as. cm that's the answer
Find the amount of money in the account after 6 years at 4% APR compounded monthly if $18000 were inititally deposited
Answers
Answer:
22,873.35
Step-by-step explanation:
A=p+I where P(principal) = 18,000
I(interest) = 4,873.35
Answer:
A = 22,775
Step-by-step explanation:
A = amount after 6 years
P = 18,000
r = 4% (in decimal = 0.04)
t = 6 years
A = 18,000 ( 1 + 0.04)^6
A = 22,775

how many ft is equal to 1.66m
Answers
Answer:
5.44 meters
Step-by-step explanation:
We Know
0.3048 meter = 1 ft
How many ft makes a height of 1.66m?
We Take
1.66 ÷ 0.3048 ≈ 5.44 meters
So, the answer is 5.44 meters.
fill out the missing angle measures until you find x

Answers
Answer: I think 131
Step-by-step explanation:
If (x + k) is a factor of f(x), which of the following must be true?
f(K) = 0
fl-k)=0
A root of f(x) is x = k.
A y intercept of f(x) is x = -k.
Answers
Answer:
f(-k)=0Step-by-step explanation:
(x + k) is a factor of f(x)
x+k=0 => x= -k; -k is a root of f(x)
=> f(-k)=0
\((x + k) is a factor of f(x)x+k=0 = > x= -k; -k is a root of f(x)= > f(-k)=0\)
So the correct option is B.fl-k)=0.
What is a root function example?
The cube root function is f(x)=3√x f ( x ) = x 3 . A radical function is a function that is defined by a radical expression. The following are examples of rational functions: f(x)=√2x4−5 f ( x ) = 2 x 4 − 5 ; g(x)=3√4x−7 g ( x ) = 4 x − 7 3 ; h(x)=7√−8x2+4 h ( x ) = − 8 x 2 + 4 7 .
What is the root function?
The root function is used to find a single solution to a single function with a single unknown. In later sections, we will discuss finding all the solutions to a polynomial function. We will also discuss solving multiple equations with multiple unknowns. For now, we will focus on using the root function.
Learn more about root function here: https://brainly.com/question/13136492
#SPJ2
(b) Given one of the zeros of equation 2x³ - 23x + 78x +k=0 is 3/2
Find value k, hence,
solve the equation.
Answers
Answer:
k = -55 x - 2 x^3
Step-by-step explanation:
Solve for k:
2 x^3 + 55 x + k = 0
Hint: | Solve for k.
Subtract 2 x^3 + 55 x from both sides:
Answer: k = -55 x - 2 x^3
3/2 is not a Root of this equation - see below, those are the Roots/Zeros.
Solve for x:
2 x^3 + 55 x + k = 0
Divide both sides by 2:
x^3 + (55 x)/2 + k/2 = 0
Change coordinates by substituting x = y + λ/y, where λ is a constant value that will be determined later:
k/2 + 55/2 (y + λ/y) + (y + λ/y)^3 = 0
Multiply both sides by y^3 and collect in terms of y:
y^6 + y^4 (3 λ + 55/2) + (k y^3)/2 + y^2 (3 λ^2 + (55 λ)/2) + λ^3 = 0
Substitute λ = -55/6 and then z = y^3, yielding a quadratic equation in the variable z:
z^2 + (k z)/2 - 166375/216 = 0
Find the positive solution to the quadratic equation:
z = 1/36 (sqrt(3) sqrt(27 k^2 + 332750) - 9 k)
Substitute back for z = y^3:
y^3 = 1/36 (sqrt(3) sqrt(27 k^2 + 332750) - 9 k)
Taking cube roots gives (sqrt(3) sqrt(27 k^2 + 332750) - 9 k)^(1/3)/6^(2/3) times the third roots of unity:
y = (sqrt(3) sqrt(27 k^2 + 332750) - 9 k)^(1/3)/6^(2/3) or y = -((-1)^(1/3) (sqrt(3) sqrt(27 k^2 + 332750) - 9 k)^(1/3))/6^(2/3) or y = ((-1)^(2/3) (sqrt(3) sqrt(27 k^2 + 332750) - 9 k)^(1/3))/6^(2/3)
Substitute each value of y into x = y - 55/(6 y):
x = (sqrt(3) sqrt(27 k^2 + 332750) - 9 k)^(1/3)/6^(2/3) - 55/(6^(1/3) (sqrt(3) sqrt(27 k^2 + 332750) - 9 k)^(1/3)) or x = -(55 (-1)^(2/3))/(6^(1/3) (sqrt(3) sqrt(27 k^2 + 332750) - 9 k)^(1/3)) - ((-1)^(1/3) (sqrt(3) sqrt(27 k^2 + 332750) - 9 k)^(1/3))/6^(2/3) or x = (55 ((-1)/6)^(1/3))/(sqrt(3) sqrt(27 k^2 + 332750) - 9 k)^(1/3) + ((-1)^(2/3) (sqrt(3) sqrt(27 k^2 + 332750) - 9 k)^(1/3))/6^(2/3)
Bring each solution to a common denominator and simplify:
Answer: x = (6^(1/3) (sqrt(81 k^2 + 998250) - 9 k)^(2/3) - 55 6^(2/3))/(6 (sqrt(81 k^2 + 998250) - 9 k)^(1/3)) or x = -((-1)^(1/3) ((sqrt(81 k^2 + 998250) - 9 k)^(2/3) + 55 (-6)^(1/3)))/(6^(2/3) (sqrt(81 k^2 + 998250) - 9 k)^(1/3)) or x = ((-1)^(1/3) ((-1)^(1/3) (sqrt(81 k^2 + 998250) - 9 k)^(2/3) + 55 6^(1/3)))/(6^(2/3) (sqrt(81 k^2 + 998250) - 9 k)^(1/3))
Ian gets $9.00 for each hour he works. He also gets $10.00 for each day he works. He made the equation y=9x+10x where x is the number of hours he works.
Explain why his equation will not tell him how much he makes in a day.
Answers
Which of the following python methods can be used to perform simple...
Which of the following python methods can be used to perform simple linear regression on a data set? Select all that apply.
Question 3 options:
A. linregress method from scipy module
B. simplelinearregression from scipy module
C. ols method from statsmodels module
Answers
The python methods that can be used to perform simple linear regression on a data set are -
A. linregress method from scipy module
C. ols method from statsmodels module
The linregress method from the module is the most simplest and effortless method for performing simple linear on the data set. It consists of two arrays one represents the independent variables and the second represents the dependent variables.
The relationship between two variables can be modeled using simple linear regression, where the first variable is treated as the independent variable and the other as the dependent variable. Finding the line of best fit that lowers the squared sum of the residuals is the goal.
To know more about Python -
brainly.com/question/29774343
#SPJ4
2. Suppose you obtain a $3,000 T - note with a 3% annual rate, paid quarterly, with maturity in 5 years. How much interest will you earn?
Answers
Answer:
You will earn $483.55 in interest.
Step-by-step explanation:
The compound interest formula is given by:
\(A(t) = P(1 + \frac{r}{n})^{nt}\)
Where A(t) is the amount of money after t years, P is the principal(the initial sum of money), r is the interest rate(as a decimal value), n is the number of times that interest is compounded per year and t is the time in years for which the money is invested or borrowed.
$3,000 T - note with a 3% annual rate
This means that \(P = 3000, r = 0.03\)
Paid quarterly
Quarterly is 4 times per year, so \(n = 4\)
Maturity in 5 years.
This means that \(t = 5\)
How much interest will you earn?
Interest is the final amount subtracted by the principal.
Final amount:
A(5).
\(A(t) = P(1 + \frac{r}{n})^{nt}\)
\(A(5) = 3000(1 + \frac{0.03}{4})^{4*5}\)
\(A(5) = 3483.55\)
Interest:
$3,483.55 - $3,000 = $483.55
You will earn $483.55 in interest.
Felipe has a flower bed
Answers
Answer:
man thats cool
Step-by-step explanation:
A manufacturing company with 350 employees is changing the employee health insurance plan to either plan A or plan B. The company wants to know if employees have a preference between the two plans and whether or not preference differs between those employees who have family members covered under the current plan (group 1) and those who do not (group 2). The human resources office takes a simple random sample from each of the two groups, sends information about both plans to the employees in each sample, and asks them whether they prefer plan A or plan B. The table summarizes the responses received, with expected cell counts in parentheses.
Plan A Plan B Total
Yes (group 1) 40 (32.5) 20 (27.5) 60
No (group 2) 6 (13.5) 19 (11.5) 25
Total 46 39 85
Which statement is true about whether the conditions for the chi-square test for homogeneity have been met?
a. A simple random sample should have been taken from all the employees, and then each employee in the sample should have been asked their plan preference and whether or not they have family members covered under the current health insurance plan.
b. The expected cell counts are not large enough to apply the chi-square test for homogeneity.
c. The total sample size is not large enough to apply the chi-square test for homogeneity.
d. The total sample size is too large to apply the chi-square test for homogeneity.
e. All conditions necessary to apply the chi-square test for homogeneity are satisfied here.
Answers
Answer: D. The total sample size is too large to apply the chi-square test for homogeneity.
Step-by-step explanation: When sampling without replacement, the sample size should not exceed 10 percent of the population size. Here, the sample size of 85 is just over 24 percent of the population of 350 company employees.
The total sample size is too large to apply the chi-square test for homogeneity.
We have given that,
A manufacturing company with 350 employees is changing the employee health insurance plan to either plan A or plan B.
Plan A Plan B Total
yes(group 1) 40(32.5) 20(27.5) 60
No (group 2) 6 (13.5) (11.5) 25 25
Total 46 39 85
We have to find which statement is true,
What is sampling without replacement?Each sample unit of the population has only one chance to be selected in the sample. we can select one sample only way and after selection we cannot pot this sample in the sample space again.
The sample size should not exceed 10 percent of the population size.when we use sampling without replacement,
Here, the sample size of 85 is just over 25 percent of the population of 350 company employees.
Therefore,the total sample size is too large to apply the chi-square test for homogeneity.
To learn more about the sample space replacement and without replacement visit:
https://brainly.com/question/17042101
Please help I’ll mark you as brainliest if correct!

Answers
Martin flips a standard coin three times, what is the probability it lands on tails all three times?
Answers
Answer:
thirty-three percent
PreviousWhat transformations have been made from the parent graph f(x) = loga to get f(x) = 2log 2 + 1?A. vertical stretch by 2 and 1 unit in the y-directionB. vertical stretch by 2 and -1 unit in the y-directionOC. vertical stretch by 2 and 1 unit in the x-directionD. vertical stretch by 2 and -1 unit in the x-directionReset SelectionNextne

Answers
The answer is D because if we see the two graph, We can see that there is a reduction of the x values.
please answer fast...............................

Answers
The coordinate of point R after the rotation is determined as = ( - 4, 7).
option A.
What is the rotation of a figure?A rotation is a transformation that turns the figure in either a clockwise or counterclockwise direction.
You can turn a figure 90°, a quarter turn, either clockwise or counterclockwise. When you spin the figure exactly halfway, you have rotated it 180°. Turning it all the way around rotates the figure 360°.
When a figure is rotated 180 degrees, each point of the figure is moved to a new position that is exactly opposite its original position with respect to a fixed center of rotation.
The initial coordinate of point R = ( 4, 7),
The new coordinate of point R after the rotation = ( - 4, 7)
Learn more about rotation of figures here: https://brainly.com/question/13286537
#SPJ1
sin( 3pi/4 ) =
O A. 1/2
OB. -√2/2
O C. √3/2
O D. √2/2
Answers
Answer:
D
Step-by-step explanation:
sin ( 3pi / 4 )
= sin ( pi - pi / 4 )
= sin ( pi / 4 )
= 1/root(2)
= root(2) / 2
Sue can read 2 books in 2.5 hours while John reads 3 books in 5 hours. Compare the rates at which each child reads. Who can read faster? How do you know?
Answers
the sum of six consecutive even numbers of set-A is 402. what is the sum of another set-B of four consecutive numbers whose lowest number is 15 less than double the lowest number of set-A?
Answers
Let x be the lowest number in set A. Since the numbers in set A are consecutive even numbers, we know that the next number in the set is x+2, the next is x+4, and so on. We are told that the sum of the six numbers in set A is 402, so we can set up the equation:
x + (x+2) + (x+4) + (x+6) + (x+8) + (x+10) = 402
We can simplify this equation by combining like terms:
6x + 30 = 402
6x = 372
x = 62
Now, we are told that the lowest number in set B is 15 less than double the lowest number in set A. Double the lowest number in set A is 2*62 = 124, so the lowest number in set B is 124-15 = 109. Since the numbers in set B are consecutive, we know that the next number in the set is 109+1 = 110, the next is 110+1 = 111, and the final number is 111+1 = 112.
The sum of the four numbers in set B can be found by adding them together:
109 + 110 + 111 + 112 = 442
Alang is going to invest in an account paying an interest rate of 5.7% compounded
continuously. How much would Alang need to invest, to the nearest dollar, for the
value of the account to reach $113,000 in 5 years?
Answers
The investment amount is $37263.09.
What is continuous compound interest?Interest that compounded continuously to the principal amount. This interest rate provides exponential growth to period of time.
Formula of continuous compound interest rate;
P(t) = P₀ \(e^{rt}\) , where P₀ is the principal amount, r is the interest rate and t is the time period.
Given that the Alang is going to invest with the continuous compound interest rate 5.7%.
Using the formula of continuous compound interest rate,
P(t) = P₀ \(e^{rt}\)
P(t) = $113000 x \(e^{(5.7)(5)}\)
P(t) = $37263.09
Therefore, the investment amount is $37263.09.
To learn more about the continuous compound interest;
https://brainly.com/question/18722165
#SPJ1
Find the tan A and sin B exactly.
Choices -
A - tan A = 3/4, sin B =5/3
B - tan A = 4/3, sin B = 3/5
C - tan A = 3/4, sin B = 3/5
D - tan A = 4/3, sin B = 5/3

Answers
Answer:
B - tan A = 4/3, sin B = 3/5Step-by-step explanation:
First, lets find the length of the third side
b = √15² - 12² = √225 - 144 = √81 = 9Now, lets get Tan A and Sin B
Tan A = 12/9 = 4/3Sin B = 9/15= 3/5Correct option is B
Destiny wants to spend at most $240 on a video games. If each video game cost $30, what are all the possible number of games Destiny can buy?
Part A: Translate the situation into an Inequality
The inequality that best matches the situation is
Answer Choices: (30x) (x/30) (240x) (x/240)
Answer Choices: (<) (>) (> or =) (> or =)
Answer Choices: (240) (30)
Part B: Solve the Inequality from Part A
Remember to use x < or > or < underline or > underline

Answers
Answer:
30x <= 240
Step-by-step explanation:
help its pre- algebra

Answers
Answer:
bananas: 2480
plantains: 20
Step-by-step explanation:
equations:
b+p=2500
b=124p
just plug then in and solve
Answer:
20 plantains and 2480 bananas
Step-by-step explanation (b is bananas + p is plantains):
2500 = b+p
b=124*p
2500=(124*p)+p
2500=125p (divide by 125)
20=p
b=124(20)
b=2480.
20