Identify the intervals where the function is decreasing. f 5 12 X O A. (6,12) O B. (5,12) O C. (5,1) OD. (6,1) Find the absolute extremum within the specified domain. 1 Maximum of flv) = 3x2+2x2-12x-3; [ -5,11 OA. 167 -4, 6 167 - ОВ. -5, 6 OC. (-4. 95 , 3 OD. -5, 95 3
Answers
The function is decreasing in the interval (5, 6/5) and (6/5, 12). So the absolute maximum is at x = 6/5, and the absolute
minimum is at x = -5. Therefore, the answer is option A: (6/5, 167) and (-5, 132).
To find the slope, we need to take the derivative of the function.
\(f(x) = 5x^2 - 12x\)
f'(x) = 10x - 12
To find where the function is decreasing, we need to set f'(x) < 0.
10x - 12 < 0
10x < 12
x < 6/5
For the second question, we need to find the absolute extremum of the function within the given domain. To do this,
we need to find the critical points and endpoints of the domain.
\(f(x) = 3x^2 + 2x^2 - 12x - 3\)
f'(x) = 6x + 4x - 12
Setting f'(x) = 0 to find critical points:
10x - 12 = 0
x = 6/5
We also need to check the endpoints of the domain:
f(-5) = 132
f(11) = 386
for such more question on interval
https://brainly.com/question/22008756
#SPJ11
Related Questions
Mr. C is buying some Hot Cheetos for our school hangout. He can buy an 18 ounce bag for $4.50 or he can buy a 40 ounce bag of the same Cheetos for $8.80. Which bag of Hot Cheetos offers the lowest price ounce?
Answers
Answer:
Step-by-step explanation: You want to figure out how much it costs per ounce. You’ll divide $4.50/18 ounces to get $0.25 per ounce for the 18 ounce bag and $8.80/40 ounces to get $0.22 per ounce for the 40 ounce bag. The 40 ounce bag is cheaper per ounce.
If p=180−0.2D, calculate the optimal profit if the total cost is $30,500.
Answers
To calculate the optimal profit, we need to find the value of D when the total cost is \($30,500\) and then substitute it into the given equation.
To find D, we can rearrange the equation to solve for D: Given:\(p = 180 - 0.2D\) and total cost =\($30,500\) Now, substitute the total cost ($30,500) into the equation to find D:
Since D cannot be negative in this context, it means that the given equation is not applicable for a total cost of \($30,500\). it is not possible to calculate the optimal profit using the given equation and the total cost of \($30,500\).
To know more about cost visit:
https://brainly.com/question/14566816
#SPJ11
Can someone explain this

Answers
Step-by-step explanation:
n-4≥13
n≥13+4
n≥17
point the no. 17 in the number line.
Matti is making moonshine in the woods behind his house. He’s
selling the moonshine in two different sized bottles: 0.5 litres
and 0.7 litres. The price he asks for a 0.5 litre bottle is 8€, for
a
Answers
Based on the calculation, it appears that Matti had approximately 94 bottles of 0.5 litres and 11 bottles of 0.7 litres in the last patch of moonshine that he sold.
To solve the problem using the determinant method (Cramer's rule), we need to set up a system of equations based on the given information and then solve for the unknowns, which represent the number of 0.5 litre bottles and 0.7 litre bottles.
Let's denote the number of 0.5 litre bottles as x and the number of 0.7 litre bottles as y.
From the given information, we can set up the following equations:
Equation 1: 0.5x + 0.7y = 16.5 (total volume of moonshine)
Equation 2: 8x + 10y = 246 (total earnings from selling moonshine)
We now have a system of linear equations. To solve it using Cramer's rule, we'll find the determinants of various matrices.
Let's calculate the determinants:
D = determinant of the coefficient matrix
Dx = determinant of the matrix obtained by replacing the x column with the constants
Dy = determinant of the matrix obtained by replacing the y column with the constants
Using Cramer's rule, we can find the values of x and y:
x = Dx / D
y = Dy / D
Now, let's calculate the determinants:
D = (0.5)(10) - (0.7)(8) = -1.6
Dx = (16.5)(10) - (0.7)(246) = 150
Dy = (0.5)(246) - (16.5)(8) = -18
Finally, we can calculate the values of x and y:
x = Dx / D = 150 / (-1.6) = -93.75
y = Dy / D = -18 / (-1.6) = 11.25
However, it doesn't make sense to have negative quantities of bottles. So, we can round the values of x and y to the nearest whole number:
x ≈ -94 (rounded to -94)
y ≈ 11 (rounded to 11)
Therefore, based on the calculation, it appears that Matti had approximately 94 bottles of 0.5 litres and 11 bottles of 0.7 litres in the last patch of moonshine that he sold.
for such more question on litres
https://brainly.com/question/27877215
#SPJ8
Question
Matti is making moonshine in the woods behind his house. He’s selling the moonshine in two different sized bottles: 0.5 litres and 0.7 litres. The price he asks for a 0.5 litre bottle is 8€, for a 0.7 litre bottle 10€. The last patch of moonshine was 16.5 litres, all of which Matti sold. By doing that, he earned 246 euros. How many 0.5 litre bottles and how many 0.7 litre bottles were there? Solve the problem by using the determinant method (a.k.a. Cramer’s rule).
PLEASE HELP QUICK
4x^2-7x-15 factored completely.
Answers
Answer:
(4x+5)(x-3)
Step-by-step explanation:
You factor this by grouping together the numbers you get from multiplying/subtracting the numbers in the equation.
The probability of a teenager in a locality owning a bike is 0.33, of owning a car is 0.16 and of owning both is 0.11. If a teenager is chosen random from the locality, what is the probability that the teenager owns a bike or a car? a)0.34 b)0.36 c)0.38 d)0.40
Answers
Answer:
C) 0.38
Explanation:
Given the below;
p(owning a bike) = 0.33
p(owning a car) = 0.16
p(owning both) = 0.11
We'll use the below formula to determine the probability of owning a bike or a car;
\(\begin{gathered} p(\text{ owning a bike or a car) = }p(\text{ owning a bike) + p(owning a car) - p(owning both)} \\ \end{gathered}\)Substituting the given values, we'll have;
\(\begin{gathered} p(\text{ owning a bike or a car) = }0.33+0.16-0.11 \\ =0.38 \end{gathered}\)Use derivatives to solve the problem: An open-top box with a square base is to have a volume of exactly 1200 cubic inches. Find the dimensions of the box that can be made with the smallest amount of materials.
Answers
The dimensions of the box that can be made with the smallest amount of materials are approximately 16.63 inches by 16.63 inches by 4.32 inches.
To minimize the amount of material used for the open-top box with a volume of 1200 cubic inches, we need to minimize the surface area of the box. Let x be the side length of the square base and h be the height of the box.
The volume constraint is given by:
V = x^2 * h = 1200
The surface area of the box is:
A = x^2 + 4xh
We need to express the surface area A in terms of a single variable. Using the volume constraint, we can solve for h:
h = 1200 / x^2
Now substitute h into the surface area equation:
A(x) = x^2 + 4x(1200 / x^2)
To minimize A(x), we need to find the critical points by taking the derivative of A(x) with respect to x and set it to zero:
dA/dx = 2x - (9600 / x^2)
Set dA/dx = 0:
2x - (9600 / x^2) = 0
Solve for x:
x^3 = 4800
x = (4800)^(1/3) ≈ 16.63 inches
Now find h using the volume constraint:
h = 1200 / (16.63^2) ≈ 4.32 inches
So the dimensions of the box that can be made with the smallest amount of materials are approximately 16.63 inches by 16.63 inches by 4.32 inches.
To learn more about constraint, refer below:
https://brainly.com/question/30703729
#SPJ11
Need help with this

Answers
x = [?]
4x-2 3x + 14
Answers
![x = [?]4x-2 3x + 14](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/FqsBRw16T7nJJQwNqY84ea621Hvjsrpl.png)
If -2n + 6 = 36 for some value of n, what is
the value of 3n for the same value of n?
Answers
Answer:
3n = -45
Step-by-step explanation:
-2n + 6 = 36
Subtract 6 from each side
-2n +6-6 = 36-6
-2n = 30
Multiply by -3/2 on each side
-2n * -3/2 = 30 *-3/2
3n = -45
Step-by-step explanation:
first one;-
-2n+6=36
subtract 6 from both sides
-2n=30
divide both side by -2
n= -15
second one:-
what is 3n for the same value of n
n= -15
so 3n = 3× -15
=-45
;- 3n = -45
Taylor has a points card for a movie theater.
She receives 75 rewards points just for signing up.
She earns 6.5 points for each visit to the movie theater.
She needs at least 100 points for a free movie ticket.
Which inequality can be used to determine v, the minimum number of visits Taylor needs to earn her first free movie ticket?
Answers
The inequality used to determine v, the minimum number of visits Taylor needs to earn her first free movie ticket is 75 + 6.5v ≥ 100.
What are Linear Inequalities?Linear inequalities are defined as those expressions which are connected by inequality signs like >, <, ≤, ≥ and ≠ and the value of the exponent of the variable is 1.
Given,
Points for signing up = 75 points
Points for each visit to the movie theater = 6.5 points
Let v be the minimum number of visits Taylor needs to earn her first free movie ticket.
Points earned for v visits = 6.5v
She needs at least 100 points for a free movie ticket.
75 + 6.5v will be the points she earn for a free movie ticket.
This expression must be greater than 100, which is the required points for a free movie.
75 + 6.5v ≥ 100
Hence the inequality representing the situation is 75 + 6.5v ≥ 100.
Learn more about Inequalities here :
https://brainly.com/question/19516092
#SPJ1
A 10 m. DE LA CASA DE JUAN HAY UN ÁRBOL QUE DEBE SER CORTADO. JUAN TEME QUE SU CASA PUEDA SER AFECTADA AL CAER EL ÁRBOL, PERO LE ES IMPOSIBLE MEDIR DIRECTAMENTE LA ALTURA DE ÉSTE. EN ESE INSTANTE SE DA CUENTA QUE EL ÁRBOL PROYECTA UNA SOMBRA DE 4 m. Y ÉL, QUE TIENE 1,60 m. DE ESTATURA, PROYECTA UNA SOMBRA DE 80 cm. CON ÉSTOS DATOS RESOLVIÓ SU PROBLEMA Y AVERIGUÓ LA ALTURA DEL ÁRBOL, ¿CÚAL ES DICHA ALTURA?
Answers
Esta pregunta está incompleta. A continuación, la pregunta completa
A 10 m. DE LA CASA DE JUAN HAY UN ÁRBOL QUE DEBE SER CORTADO. JUAN TEME QUE SU CASA PUEDA SER AFECTADA AL CAER EL ÁRBOL, PERO LE ES IMPOSIBLE MEDIR DIRECTAMENTE LA ALTURA DE ÉSTE. EN ESE INSTANTE SE DA CUENTA QUE EL ÁRBOL PROYECTA UNA SOMBRA DE 4 m. Y ÉL, QUE TIENE 1,60 m. DE ESTATURA, PROYECTA UNA SOMBRA DE 80 cm. CON ÉSTOS DATOS RESOLVIÓ SU PROBLEMA Y AVERIGUÓ LA ALTURA DEL ÁRBOL, ¿CÚAL ES DICHA ALTURA?
A. 8 m
B. 6 m
C. 7 m
D. 10 m
E. 5 m
Answer: A. 8 m
Step-by-step explanation:
Este problema se puede solucionar con una regla de tres simple directa, la cual es aplicable cuando contamos con dos magnitudes directamente proporcionales, como las sombras/altura en este caso.
La regla de tres simple directa tiene la siguiente fórmula:
A ---- B
C ---- x
x = (B×C)÷A
En nuestro ejemplo:
sombra 0,8 m -------- altura 1,60 m
sombra 4 m -------- altura x
(4×1,60)÷0,8= 8 m (altura del árbol)
the x and y intercept

Answers
y intercept: (0, -7/3)
1a. write the general dual problem associated with the given lp. (do not transform or rewrite the primal problem before writing the general dual) maximize -4x1 2x2
Answers
The objective function of the dual problem is to minimize the sum of the products of the dual variables and the corresponding coefficients of the primal problem.
The primal problem is:
maximize -4x1 + 2x2
Subject to:
2x1 + x2 ≤ 8
x1 + 2x2 ≤ 10
x1, x2 ≥ 0
To write the general dual problem, we first need to convert the primal problem into standard form by introducing slack variables:
maximize -4x1 + 2x2
Subject to:
2x1 + x2 + s1 = 8
x1 + 2x2 + s2 = 10
x1, x2, s1, s2 ≥ 0
The general dual problem is:
minimize 8y1 + 10y2
Subject to:
2y1 + y2 ≥ -4
y1 + 2y2 ≥ 2
y1, y2 ≥ 0
Note that the coefficients of the primal problem become the constraints of the dual problem, and the constraints of the primal problem become the coefficients of the dual problem.
To learn more about function visit:
brainly.com/question/31062578
#SPJ11
a restaurant offers a choice of 4 salads, 5 main courses, and 3 desserts. how many possible 3-course meals are there?
Answers
Using the Fundamental Counting Theorem, it is found that there are 60 possible 3-course meals.
Given,
In the question:
A restaurant offers a choice of 4 salads, 5 main courses, and 3 desserts.
To find the how many possible 3-course meals are there?
Now, According to the question:
Let's know:
What is the Fundamental Counting Theorem?
It is a theorem that states that if there are n things, each with ways to be done, each thing independent of the other, the number of ways they can be done is:
\(N=n_1\) × \(n_2\) × \(n_3\)... ×\(n_n\)
In this problem, considering the number of salads, main courses and desserts, we have that:
\(n_1=4 , n_2=5,n_3=3\)
The total number of options is given by:
N = 4 × 5 × 3
N = 60
Hence, Using the Fundamental Counting Theorem, it is found that there are 60 possible 3-course meals.
Learn more about Fundamental Counting Theorem at:
https://brainly.com/question/28384306
#SPJ4
I need help
4x^2-8x-23=0
Answers
*☆*――*☆*――*☆*――*☆*――*☆*――*☆*――*☆*――*☆**☆*――*☆*――*☆*――*☆
Answer: Check the screenshot below!
Explanation:
I hope this helped!
<!> Brainliest is appreciated! <!>
- Zack Slocum
*☆*――*☆*――*☆*――*☆*――*☆*――*☆*――*☆*――*☆**☆*――*☆*――*☆*――*☆
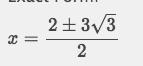
A turtle was swimming 2 feet below the surface of a pond. While looking for food, he went down 7 more feet.
Answers
Answer: 9
Step-by-step explanation:
Answer:
he's a total of 9 feet under the water
Step-by-step explanation:
Three people are using a random number generator to pick who goes first in their game the generator gives a random decimal number in hundredths between and including zero and 10 determine a fair plan for choosing who goes first and explain your reasoning
Answers
Random sampling is a fair and best plan for choosing who goes first.
Define random sampling.Each sample has an equal chance of being chosen as part of the sampling procedure known as random sampling. A randomly selected sample is intended to be a fair reflection of the entire population.
Name four types of random sampling.Simple, systematic, stratified and cluster are four types of random sampling.
In this instance, three players are choosing who goes first in their game using a random number generator. An impartial random sampling method can be used to choose participants in order to make the process fair.
To learn more about random sampling visit the link:
https://brainly.com/question/24466382
#SPJ4
The points (6,7) and (42,49) form a proportional relationship. Find the slope of the line through the points. Then use the slope to graph the line.
Answers
Answer:
The slope of the line is 6/7
Step-by-step explanation:
he weights of a large group of college football players is approximately normally distributed. it was determined that 10% of theplayers weigh less than 154 pounds and 5% weigh more than 213pounds. what are the mean and standard deviation of the distribu tion of weights of football players?
Answers
The standard deviation of the weight distribution is approximately 20.31 pounds.
Let's denote the mean of the distribution as μ (mu) and the standard deviation as σ (sigma).
From the given information, we can calculate the z-scores corresponding to the weights of 154 pounds and 213 pounds.
For the weight of 154 pounds:
The proportion of players weighing less than 154 pounds is 10%, which corresponds to a cumulative probability of 0.10. To find the z-score, we can use a standard normal distribution table or a calculator:
z = invNorm(0.10) ≈ -1.28
For the weight of 213 pounds:
The proportion of players weighing more than 213 pounds is 5%, which corresponds to a cumulative probability of 0.95 (1 - 0.05). To find the z-score, we can again use a standard normal distribution table or a calculator:
z = invNorm(0.95) ≈ 1.64
In a standard normal distribution, the z-scores represent the number of standard deviations away from the mean.
Now, we can set up two equations using the z-scores:
1.28 = (154 - μ) / σ --> (1)
-1.64 = (213 - μ) / σ --> (2)
Solving these equations simultaneously will give us the mean (μ) and the standard deviation (σ) of the weight distribution.
Let's solve these equations:
From equation (1):
1.28σ = 154 - μ
From equation (2):
-1.64σ = 213 - μ
Adding equation (1) and equation (2):
1.28σ - 1.64σ = 154 - μ + 213 - μ
-0.36σ = 367 - 2μ
Simplifying:
-0.36σ = 367 - 2μ
0.36σ = 2μ - 367
Dividing by 0.36:
σ = (2μ - 367) / 0.36
Substituting this value of σ in equation (1):
1.28σ = 154 - μ
1.28[(2μ - 367) / 0.36] = 154 - μ
Simplifying:
1.28(2μ - 367) = 0.36(154 - μ)
2.56μ - 470.16 = 55.44 - 0.36μ
Combining like terms:
2.56μ + 0.36μ = 470.16 + 55.44
2.92μ = 525.6
Dividing by 2.92:
μ = 525.6 / 2.92
μ ≈ 180.00
Now that we have the value of μ, we can substitute it into equation (1) to find σ:
1.28σ = 154 - μ
1.28σ = 154 - 180
1.28σ = -26
Dividing by 1.28:
σ = -26 / 1.28
σ ≈ -20.31
Since standard deviation cannot be negative, we can disregard the negative sign. The standard deviation of the weight distribution is approximately 20.31 pounds.
To summarize:
Mean (μ) ≈ 180 pounds
Standard Deviation (σ) ≈ 20.31 pounds
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
How to round 8.6023 in the nearest tenth?
Answers
Answer:
8.6
Step-by-step explanation:
https://www.you.tube.com/watch?v=32gDF10ZXOA
( it might be wrong pls dont report me just let me kno y its wrong )
Answer:
8.6
Step-by-step explanation:
First of all consider the thousands in the decimal which is 2. Since 2 is not greater than 5 we have to remove the number 2 and 3 from the 8.6023.
We're left with 8.60. Now we see that there's a 0 in the hundredths so since it's not greater than 5 we remove it.
Now we're left with 8.6 which is to the nearest tenth.
a measurable part of a line that consists of two points, called endpoints, and all of the points between them are
Answers
A measurable part of a line that consists of two points, called endpoints, and all of the points between them are called Line sigments.
Geometry is a branch of mathematics that deals with how objects can be expressed as relationships of points, lines, planes, surfaces, and dimensions. When we draw lines in geometry, we use an arrow at each end to show that it expands infinitely. A line is a path between two points that can be measured. Since line segments have a defined length, they can form the sides of any polygon. The figure below shows the line AB, where the length of the line AB is related to the distance between its endpoints, A and B. The symbol for the line is named after its two endpoints, e.g.
\( \bar{AB}\)
To learn more about line segment, refer:
https://brainly.com/question/28962970
#SPJ4

Suppose that f(x)= √(3x−3) and g(x)=6x^2−8.
For each function h given below, find a formula for h(x) and the domain of h. Enter the domains using interval notation. (A) h(x)=(f∘g)(x) h(x)= Domain = (B) h(x)=(g∘f)(x). h(x)= Domain = (C) h(x)=(f∘f)(x). h(x)= Domain = (D) h(x)=(g∘g)(x). h(x)= Domain =
Answers
(A) h(x) = (f∘g)(x)
= √(3(6x^2−8)−3)
= √(18x^2−24−3)
= √(18x^2−27).
Domain of h: All real numbers since the square root is defined for all real numbers.
(B) h(x) = (g∘f)(x)
= 6(√(3x−3))^2−8
= 6(3x−3)−8
= 18x−26.
Domain of h: All real numbers since the function g(x) = 6x^2−8 is defined for all real numbers.
(C) h(x) = (f∘f)(x)
= √(3(√(3x−3))−3)
= √(3√(3x−3)−3).
Domain of h: The expression inside the square root must be non-negative, so 3x−3 ≥ 0.
Solving this inequality, we get x ≥ 1.
Therefore, the domain of h is [1, +∞).
(D) h(x) = (g∘g)(x)
= 6((6x^2−8)^2)−8
= 6(36x^4−96x^2+64)−8
= 216x^4−576x^2+376.
Domain of h: All real numbers since the function g(x) = 6x^2−8 is defined for all real numbers.
To find the formulas for each function h(x) and the domain of h, we need to substitute the given functions f(x) and g(x) into the compositions (f∘g)(x), (g∘f)(x), (f∘f)(x), and (g∘g)(x).
(A) (f∘g)(x):
Substitute g(x) = 6x^2−8 into f(x) = √(3x−3):
h(x) = (f∘g)(x)
= √(3(6x^2−8)−3)
= √(18x^2−24−3)
= √(18x^2−27).
(B) (g∘f)(x):
Substitute f(x) = √(3x−3) into g(x) = 6x^2−8:
h(x) = (g∘f)(x)
= 6(√(3x−3))^2−8
= 6(3x−3)−8
= 18x−26.
(C) (f∘f)(x):
Substitute f(x) = √(3x−3) into itself:
h(x) = (f∘f)(x)
= √(3(√(3x−3))−3)
= √(3√(3x−3)−3).
(D) (g∘g)(x):
Substitute g(x) = 6x^2−8 into itself:
h(x) = (g∘g)(x)
= 6((6x^2−8)^2)−8
= 6(36x^4−96x^2+64)−8
= 216x^4−576x^2+376.
The domains of each function h(x) depend on the restrictions on x imposed by the square root and the inequality.
The formulas and domains for the given functions h(x) are:
(A) h(x) = √(18x^2−27), Domain: All real numbers.
(B) h(x) = 18x−26, Domain: All real numbers.
(C) h(x) = √(3√(3x−3)−3), Domain: [1, +∞).
(D) h(x) = 216x^4−576x^2+376, Domain: All real numbers.
To know more about square root, visit
https://brainly.com/question/91924
#SPJ11
Un camion lleva 200 cajas. Cada caja contiene 20 paquetes de cafe de un cuarto de kilo. ?Cuantos kilos de cafe lleva el camion?
Answers
Answer:
1000 cajas
Step-by-step explanation:
De la pregunta anterior, sabemos que:
Un camión lleva 200 cajas.
Cada caja contiene 20 paquetes de café de un cuarto de kilo.
Esto significa
1 caja = 20 paquetes (1/4 kilo) de café
1 caja = paquetes de 5 kilos de café
Ya que tenemos 200 cajas en el camión
1 caja = 5 kilo
200 cajas = x
Cruz multiplicar
x = 200 × 5 kilo
x = 1000 kilos
Por tanto, los kilos de café que puede transportar el camión son 1000 kilos.
HELPPPPPPPPPPPP PLEASEEEE

Answers
Answer:
H. 13.5 in²
Step-by-step explanation:
\(V=LWH/3\)
\(V=(3)(3)(4.5)/3\)
\(V=13.5 in^{2}\)
--------------------
hope it helps...
have a great day!!
Michael invested a total of $14,000 in two certificates of deposit. One pays 5% interest,
and the other pays 6% interest. His total interest at the end of one year is $780. How
much is invested in the CD that pays 5% interest?
Answers
Answer:
6000=5%
8000=other CD
Step-by-step explanation:
Solve the system of equations.
- 9x - 6y = 15
9x – 10y = 145
X =
Y =
Answers
HELP PLEASE! DELTA MATH! THANKS!
Last year at a certain high school, there were 140 boys on the honor roll and 68 girls on the honor roll. This year, the number of boys on the honor roll increased by 5% and the number of girls on the honor roll increased by 25%. By what percentage did the total number of students on the honor roll increase? Round your answer to the nearest tenth (if necessary).
Answers
Answer:
11.5
Step-by-step explanation:
Find new values:
140(1+0.05)=147
68(1+0.25)=85
Last Year This Year
Boys 140 147
Girls 68 85
Total 208 232
Find overall increase:
208(1+r)=232
1+r=1.115385
r=0.115385
Final Answer: 11.5%
The total number of students on the honor roll increased by 11.5%.
What is the percentage?The percentage is defined as a ratio expressed as a fraction of 100.
The percentage increase in the number of boys on the honor roll is 5%, which means that the number of boys on the honor roll this year is 1.05 times the number of boys on the honor roll last year:
1.05 x 140 = 147
The percentage increase in the number of girls on the honor roll is 25%, which means that the number of girls on the honor roll this year is 1.25 times the number of girls on the honor roll last year:
1.25 x 68 = 85
Therefore, the total number of students on the honor roll this year is:
147 + 85 = 232
The percentage increase in the total number of students on the honor roll is:
((232 - 208) / 208) x 100% = 11.5385%
Rounding to the nearest tenth gives an answer of 11.5%.
Therefore, the total number of students on the honor roll increased by 11.5%.
Learn more about percentages here:
brainly.com/question/24159063
#SPJ3
Binomial Problem:A jury has 12 jurors. A vote of at least 10 out of 12 for "guilty" is necessary for a defendant to be convicted of a crime. Assume that each juror acts independently of the others and that the probability that any one juror makes the correct decision on a defendant is .80. If the defendeant is guitly, what is the probability that the jury makes the correct decision?
Answers
The probability that the jury makes the correct decision is approximately 0.7063.
To solve this problem, we need to find the probability that the jury makes the correct decision if the defendant is guilty. Let's break down the problem into smaller steps.
We know that the probability of a single juror making the correct decision is 0.80. If the defendant is guilty, then the probability of a juror making the correct decision is still 0.80. Therefore, the probability that a single juror makes the correct decision if the defendant is guilty is 0.80.
We can use the binomial distribution formula to determine the probability of at least 10 out of 12 jurors making the correct decision. The formula is:
P(X ≥ k) = 1 - Σ(i=0 to k-1) [n!/(i!(n-i)!) x \(p^i \times (1-p)^{(n-i)}\) ]
where:
P(X ≥ k) is the probability of at least k successes
n is the total number of trials (in this case, 12 jurors)
p is the probability of success in a single trial (in this case, 0.80)
k is the number of successes we want to find the probability of (in this case, 10)
Plugging in the values, we get:
P(X ≥ 10) = 1 - Σ(i=0 to 9) [12!/(i!(12-i)!) x \(0.80^i \times (1-0.80)^{(12-i)}\)]
Using a calculator or software, we can calculate this to be approximately 0.7063.
To know more about probability here
https://brainly.com/question/11234923
#SPJ4
Rewrite each equation without absolute value for the given conditions.
(Please help)ASAP
1. y = |x − 3| + |x +2| − |x − 5| if x >5
2. y = |x − 3| + |x +2| − |x − 5| if x < −2
3. y = |x − 3| + |x +2| − |x − 5| if 3
Answers
The equations without absolute value for the given conditions are: 1. y = -3x + 6 if x > 5; 2. y = -x - 6 if x < -2; 3. y = x - 6 if 3 ≤ x ≤ 5, and y = -x - 6 if x < 3.
1. When x > 5, the expression (x - 3) is positive, (x + 2) is positive, and (x - 5) is positive. Thus, to get absolute value we can rewrite the equation as:
y = (x - 3) + (x + 2) - (x - 5)
Simplifying this, we get:
y = 2x - 4
2. When x < -2, the expression (x - 3) is negative, (x + 2) is negative, and (x - 5) is negative. Thus, we can rewrite the equation as:
y = -(x - 3) - (x + 2) + (x - 5)
Simplifying this, we get:
y = -2x + 6
3. When -2 ≤ x ≤ 3, the expression (x - 3) is negative, (x + 2) is positive, and (x - 5) is negative. Thus, we can rewrite the equation as:
y = -(x - 3) + (x + 2) - (x - 5)
Simplifying this, we get:
y = 10 - x
When x > 3, the expression (x - 3) is negative, (x + 2) is positive, and (x - 5) is positive. Thus, we can rewrite the equation as:
y = -(x - 3) + (x + 2) + (x - 5)
Simplifying this, we get:
y = -2x + 6
To learn more about absolute value please click on below link
https://brainly.com/question/29764645
#SPJ1