Identify the angles of rotational symmetry for the figure.
there can be more than one options
Answers
Related Questions
To find the number in a square, multiply the numbers in the two circles connected to it. Fill in the missing numbers.
Answers
The details of the relationship between the numbers is a word problem that can be used to find the values in the other missing values as presented in the attached drawing .
What is a word problem?A word problem is a presentation of a mathematical question using verbal statements.
Please find attached the possible diagram in the question obtained from a similar question posted online
The value in the square is -6
The value in the circle to the top right of the square = -3
Therefore;
The value in the circle in the bottom left corner (in the triangular arrangement) of the square = -6 ÷ -3 = 2The value in the circle to the right of the square with 12 is therefore found by dividing 12 by the value of the circle to the left of 12 as follows;
12 ÷ 2 = 6
The value in the circle to the right of the square containing 12 is 6The value in the blank square is the product of the values in the two circles (The circle at the top (-3) and the circle at the bottom right (6) of the triangle) as follows;
Value in the square left blank = -3 × 6 = -18The figure completed with the missing values in the circles and squares are presented in the attached drawing created with MS Word
Learn more on word problems here: https://brainly.com/question/2057972
#SPJ1
Katie has a collection of nickels dimes and quarters with a total value of $4.60. there are 6 more dimes than nickels and 8 more quarters than nickels. How many of each coins does she have?
Answers
Answer:
920
Step-by-step explanation:
$4.60×6-8
$4.60×2dimes
=920
Refer to the given terms . A pattern defines the relationship between the first two terms . Determine the relationship and identify the missing term of the second pair , such that both the pairs are analogous . AZP : ZAR :: TXK :
Answers
The missing term in the second pair is YUL.
To determine the relationship between the first two terms, let's analyze the given pattern: AZP : ZAR.
If we look closely, we can observe that each letter in the first term is shifted one position forward in the alphabet to form the corresponding letter in the second term.
So, applying the same pattern to the second pair (TXK), we need to shift each letter one position forward in the alphabet:
T + 1 = U
X + 1 = Y
K + 1 = L
Therefore, the missing term in the second pair is YUL.
The analogy between the pairs is that each letter in the first term is shifted one position forward in the alphabet to form the corresponding letter in the second term.
Learn more about sequence here:
https://brainly.com/question/28694302
#SPJ1
In the figure below, AMNO
APQR. Determine the length of QR.
M
2y + 3
4x-2
x+ y
R
21
9
O 14
O3
O 12
Answers
Given:
\(\Delta MNO\cong \Delta PQR\)
To find:
The length of QR.
Solution:
We have,
\(\Delta MNO\cong \Delta PQR\)
Then, \(MN=PQ\) (CPCTC)
\(10=4x-2\)
\(10+2=4x\)
\(12=4x\)
Divide both sides by 4.
\(\dfrac{12}{4}=x\)
\(3=x\)
Similarity,
\(MO=PR\) (CPCTC)
\(2y+3=21\)
\(2y=21-3\)
\(2y=18\)
Divide both sides by 2.
\(y=9\)
Now,
\(x+y=3+9\)
\(x+y=12\)
Therefore, the correct option is d.
2) Cost of a microscope: $269.95 Markup: 43% Tax: 5%
Answers
Answer:
386.0285
Step-by-step explanation:
Answer:
$405.33
Step-by-step explanation:
I assume you are looking for the final sale price including the markup and tax.
original cost: $269.95
To add the markup of 43%, we multiply the cost by 1.43. To add the tax of 5%, we multiply by 1.05.
final sale price = 1.05 × 1.43 × $269.95
final sale price = $405.33
Nicole bought six pounds of apples at $1.50 per pound. The store had a discount of $2 Nicole bought six pounds of apples at $1.50 per pound. The store had a discount of $2 off her total purchase. Nicole and her friend then divided the cost of the purchase evenly. Which expression can be used to determine how much Nicole and her friend each paid for the apples? Nicole bought six pounds of apples at $1.50 per pound. The store had a discount of $2 off her total purchase. Nicole and her friend then divided the cost of the purchase evenly. Which expression can be used to determine how much Nicole and her friend each paid for the apples?Nicole bought six pounds of apples at $1.50 per pound. The store had a discount of $2 off her total purchase. Nicole and her friend then divided the cost of the purchase evenly. Which expression can be used to determine how much Nicole and her friend each paid for the apples?Nicole bought six pounds of apples at $1.50 per pound. The store had a discount of $2 off her total purchase. Nicole and her friend then divided the cost of the purchase evenly. Which expression can be used to determine how much Nicole and her friend each paid for the apples? Nicole bought six pounds of apples at $1.50 per pound. The store had a discount of $2 off her total purchase. Nicole and her friend then divided the cost of the purchase evenly. Which expression can be used to determine how much Nicole and her friend each paid for the apples? Nicole bought six pounds of apples at $1.50 per pound. The store had a discount of $2 off her total purchase. Nicole and her friend then divided the cost of the purchase evenly. Which expression can be used to determine how much Nicole and her friend each paid for the apples?
Answers
6 pounds * $1.50 per pound = $9
Then, we can subtract the discount:
$9 - $2 = $7
Since Nicole and her friend split the cost evenly, we can divide $7 by 2:
$7 / 2 = $3.50
Therefore, each of them paid $3.50 for the apples.
The expression that can be used to determine this is:
($6 * $1.50 - $2) / 2 = $3.50
where $6 is the total cost of 6 pounds of apples at $1.50 per pound and $2 is the discount
Find the area, in square units, of rectangle ABCD plotted below. A (-4,5) B (-2,-3) C (2,-2) D (0,6)
Answers
Answer:
The answer is: D) 34
Write the expression in repeated multiplication form. Then write the expression as a power. 56.53 The expression in repeated multiplication form is The expression as a power is
Answers
We have the following:
\(5^6\cdot5^3\)When two numbers with the same base are multiplied, only their power is added, therefore
\(5^6\cdot5^3=5^{6+3}=5^9\)The expression in repeated multiplication form is 5*5*5*5*5*5*5*5*5
The expression as a power is 5^9
Last year at a certain high school, there were 124 boys on the honor roll and 125 girls on the honor roll. This year, the number of boys on the honor roll decreased by 25% and the number of girls on the honor roll decreased by 20%. By what percentage did the total number of students on the honor roll decrease? Round your answer to the nearest tenth (if necessary).
Answers
Answer:
22.5%
Step-by-step explanation:
Find new values:
124(1−0.25)=93
125(1−0.2)=100
Last Year: Boys 124 & Girls 125
This Year: Boys 93 & Girls 100
Total: Last Year 249 & This Year 193
249(1−r)=193
249(1−r)/249=193/249
1−r=0.7751
−r=−0.2249(Subtracted 1)
r=0.2249(Divided by -1)
Final Answer: 22.5%(Multiply by 100 and round to nearest 10th)
Complete each statement. If the triangles cannot be shown to be congruent from the information given, leave the triangle's name blank and write Can not be Determined (CNBD) in the spot for rule.
By rule ________ ∆SAT ≅ Δ____ By rule ________
Answers
The completed statement that specifies the rule of congruency between triangle ΔSAT and triangle ΔSAO, is as follows;
ΔSAT ≅ ΔSAO by SAA rule.
What are congruent triangles?Two triangles, ΔA and ΔB are congruent if the three lengths of the sides of triangle ΔA are congruent to the three side lengths of triangle ΔB.
The possible dimensions of the triangles, obtained from the triangle diagrams in a similar question on the site are;
Side ST in triangle ΔSAT is congruent to side SO in triangle ΔSAO
Angle ∠AST in triangle ΔSAT is congruent to angle ∠ASO in triangle ΔSAO
Side SA is congruent to side SA by reflexive property of congruency
Therefore, a side, (ST) an included angle (∠AST) and another side (SA), in triangle ΔSAT are congruent to a side (SO), an included angle (∠ASO), and another side SA in triangle ΔSAO
Therefore, triangle ΔSAT is congruent to triangle ΔASO, by Side-Angle-Side, SAS, congruency ruleLearn more about the triangle congruency rules here:
https://brainly.com/question/3580004
#SPJ1
Please please please help me
I really need to pass this I will give brainliest and a lot of points please just help me solve this correctly
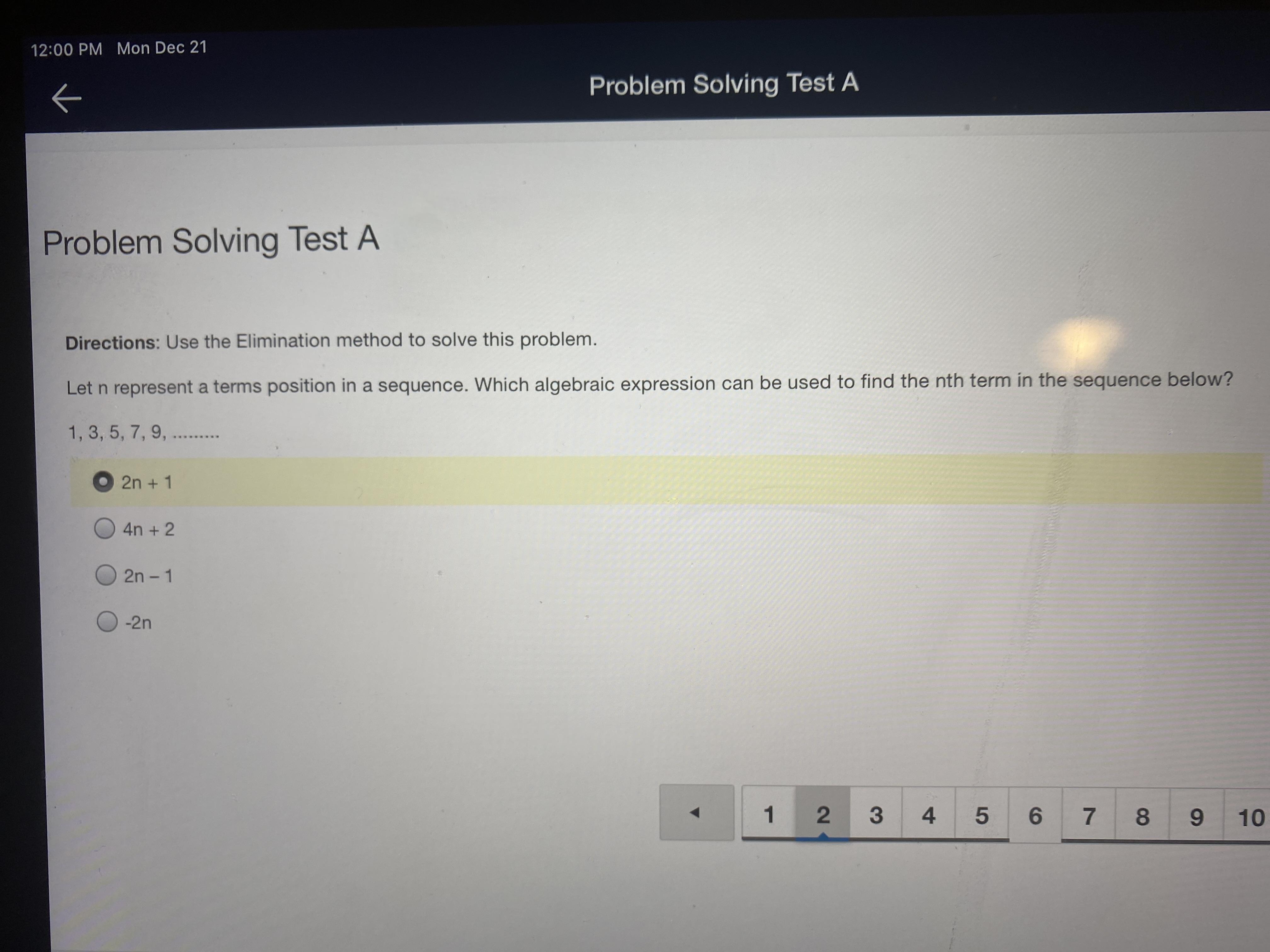
Answers
The length of side AB is about 5.87 units.
How to find the side of a right triangle?The triangle ABC is a right angle triangle. A right angle triangle is a triangle that has one of its angles as 90 degrees.
Therefore, let's find the length AB in the right triangle.
Using trigonometric ratios,
cos 33 = adjacent / hypotenuse
Therefore,
Adjacent side = AB
hypotenuse side = 7 units
cos 33° = AB / 7
cross multiply
AB = 7 cos 33
AB = 7 × 0.83867056794
AB = 5.87069397562
AB = 5.87 units
learn more on right triangle here: https://brainly.com/question/30966657
#SPJ1
22. How many positive integers less than 1000 a) are divisible by 7? b) are divisible by 7 but not by 11? c) are divisible by both 7 and 11? d) are divisible by either 7 or 11? e) are divisible by exactly one of 7 and 11? f ) are divisible by neither 7 nor 11? g) have distinct digits? h) have distinct digits and are even?
Answers
The set of positive integers less than 1000 that are:
a)Divisible by 7 are 142
b)Divisible by 7 but not by 11 are 130
c)Divisible by both 7 and 11 are 12
d)Divisible by either 7 or 11 are 220
e)Divisible by exactly one of 7 and 11 are 220
f)Divisible by neither 7 nor 11 are 780
g)Having distinct digits are 576
h)Having distinct digits and even are 337
We have,
A whole number that is greater than zero is known as positive integer
a)The positive numbers below 1000 that are divisible by 7 are 7, 14, 21, 28,..., 994.
Total terms: 994, divided by 7, plus (n-1)
There are 142 total terms below 1000 that are divisible by 7.
b) The numbers 77, 154, 231, 308, 385, 462, 539, 616, 693, 770, 847, and 924 are all divisible by both 7 and 11.
The total number of integers below 1000 that are divisible by 7 but not 11 therefore equals 142 - (total number of integers divisible by 7 and 11), which means that the total number of integers that fall into this category is 130.
c) The total amount of integers that can be divided by both 7 and 11 equals the total amount of integers that can be divided by 77.
There are 12 total integers below 1000 that can be divided by 77.
d) The total number of integers that can be divided by either 7 or 11 is equal to the sum of the numbers that can be divided by each of those numbers and the number that can be divided by 77.
The total number of integers below 1000 that are divisible by 11 is (11,22,33,...,990). 990 = 11 + (n-1) 11, which equals 90 integers.
Total integers that may be divided by both 7 and 11 are equal to 142 + 90 - 12 = 220.
e) The total number of integers that may be divided by either 7 or 11 perfectly is equal to 142 + 90 - 12 = 220 numbers.
f) The total number of integers that cannot be divided by either 7 or 11 is 1000 - (The total number of integers that can be divided by either 7 or 11), which is 1000 - 220 = 780 numbers.
g)Distinct digits from 1 to 100 = 100 - Total number of integers below 1000 with distinct digits = 1000 - (non-distinct digits) ( 11,22,33,44,55,66,77,88,99,100),
=> Unique digits from 1 to 100 equal 90.
=> The distinct numerals 101 to 200 equal 100. (101,110,111,112,113,114,115,116,117,118,119,121,122,131,133,141,144,151,155,161,166,171,177,181,188,191,199,200),
=> Unique digits from 101 to 200 are: 100 to 28, 72.
=> Unique numbers between 201 and 1000 = 72 x 8 = 576.
h)Different digits and even values equal to 337
To know more about positive integers, visit:
brainly.com/question/13733829
#SPJ1
Ms. Chung drives the same distance to go to work every Monday through Friday. On Saturday she drove g the distance she drives to work. The distance she drove on Saturday was 0.9 miles. Part A: In the first box, enter an equation to represent the distance, d, that Ms. Chung drives to work. Part B: In the second box, enter the distance Ms. Chung drives to work.
Answers
A) The algebraic expression will be 12d + 7 = 91
B) He drives 7 miles per day to work.
For 11 days straight, Ms. Chung drove the same distance every day going to and coming from work.
The distance she drove on Saturday was; 0.9 miles.
The number of miles she drives per day:
84 miles/12
= 7 miles per day
Let the number of miles she travels be day = d
12d + 7 = 91 miles
12d + 7 = 91
12d = 91 - 7
12d = 84
d = 84/12
d = 7 miles per day
Learn more about equations here;
https://brainly.com/question/25180086
#SPJ1
What is the distance between the points (-1,4) and (7,4)?
Answers
Answer:
8
Step-by-step explanation:
=(7−(−1))2+(4−4)2‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾√
=(8)2+(0)2‾‾‾‾‾‾‾‾‾‾√
=64+0‾‾‾‾‾‾√
=6‾√4
=8
In a certain chemical, the ratio of zinc to copper is 3 to 19. A jar of the chemical contains 874 grams of copper. How many grams of zinc does it contain?
It contains
grams of Zinc
Answers
Answer:
138 grams of zinc
Step-by-step explanation:
Zinc : copper = 3 : 19
Let amount of zinc = 138 grams
3 : 19 :: x : 874
Product of means = product of extremes
19 * x = 3 * 874
x = \(\frac{3*874}{19}\)
x = 3 * 46
Zinc = 138 grams
\(\underline{\underline{\sf \bigstar \qquad Solution \qquad \: \bigstar}} \\ \)
Copper and Zinc in the ratio = 3:19Weight of copper in chemical = 874 gramsLet weight of copper be 3x and weight of zinc be 19x.
☯ \(\underline{\boldsymbol{According\: to \:the\: Question\:now :}} \\\)
\(:\implies \textsf {Total weight = weight of copper + weight of zinc} \\ \\ \\ \)
\(:\implies \textsf {Total weight = 3x +19x} \\ \\ \\ \)
\(:\implies \underline{ \boxed{ \textsf {Total weight = 22x}}} \\ \\ \\ \)
⠀⠀━━━━━━━━━━━━━━━━━━━━━━━━
\(\dashrightarrow\:\:\textsf{ Weight of chemical = weight of zinc + weight of copper} \\ \\ \\ \)
\(\dashrightarrow \: \: \sf 22x = 3x + 19x \\ \\ \\ \)
\(\dashrightarrow \: \: \sf 22x = 3x + 874 \\ \\ \\ \)
\(\dashrightarrow \: \: \sf 22x - 3x = 874 \\ \\ \\ \)
\(\dashrightarrow \: \: \sf 19x = 874 \\ \\ \\ \)
\(\dashrightarrow \: \: \sf x = \dfrac{874}{19} \\ \\ \\ \)
\(\dashrightarrow \: \: \underline{\boxed{ \sf x = 46}} \\ \\ \\\)
⠀⠀━━━━━━━━━━━━━━━━━━━━━━━━━━━
\(\bigstar\:\underline{\frak{Finding \: the \: weight \: of \: the \: zinc \: in \: a \: chemical : }}\)
\(\longrightarrow\:\:\sf weight \: of \: zinc = 3x \\ \\ \\ \)
\(\longrightarrow\:\:\sf weight \: of \: zinc = 3 \times 46 \\ \\ \\ \)
\(\longrightarrow\:\: \underline{ \boxed{\sf weight \: of \: zinc =138 \: grams}} \\ \\ \\ \)
\(\therefore\:\underline{\textsf{The chemical contains \textbf{138 grams}} \textsf{ of zinc}}. \\ \)
Mark what answer it is
Answers
2/29
the i is imaginary
help me please
I need fast
Answers
Answer:
48 is the answer because if you were to have been remembering past questions that has that same picture but answered it would be 48
1. What is the theoretical probability that the family has two dogs or two cats?
2. Describe how to use two different coins to simulate which two pets the family has.
3. Flip both coins 50 times and record your data in a table like the one below.
Result Frequency
Heads, Heads
Heads, Tails
Tails, Heads
Tails, Tails
Total 50
1. Based on your data, what is the experimental probability that the family has two dogs or two cats?
2. If the family has three pets, what is the theoretical probability that they have three dogs or three cats?
3. How could you change the simulation to generate data for three pets?
Answers
The theoretical probability of having three dogs or three cats is p^3 + q^3.
The theoretical probability of the family having two dogs or two cats depends on the specific probability of each event. Let's assume that the probability of having a dog is 0.5 and the probability of having a cat is also 0.5 (which is a simplification). In this case, the probability of having two dogs is 0.5 x 0.5 = 0.25, and the probability of having two cats is also 0.5 x 0.5 = 0.25. Therefore, the theoretical probability of the family having two dogs or two cats is 0.25 + 0.25 = 0.5 or 50%.
To simulate which two pets the family has using two different coins, we can assign one pet to each coin face (e.g., heads for dog and tails for cat). Then, we can flip both coins and record the outcome to determine which pets the family has. For example, if the first coin shows heads and the second coin shows tails, the family has one dog and one cat.
After flipping both coins 50 times and recording the outcomes in a table, we can calculate the experimental probability of the family having two dogs or two cats. Let's assume that we observed 12 occurrences of two dogs, 10 occurrences of two cats, and 28 occurrences of other outcomes (e.g., one dog and one cat). The experimental probability of the family having two dogs or two cats is (12 + 10) / 50 = 0.44 or 44%.
If the family has three pets, the theoretical probability of having three dogs or three cats can be calculated using a similar approach. Let's assume that the probability of having a dog is p and the probability of having a cat is q (where p + q = 1). Then, the probability of having three dogs is p x p x p = p^3, and the probability of having three cats is q x q x q = q^3. Therefore, the theoretical probability of having three dogs or three cats is p^3 + q^3.
To learn more about Probability :
https://brainly.com/question/24756209
#SPJ11
Divide the complex numbers and express answer in the form (a+bi)
3-4i/8+2i
Answers
Answer:
\(\frac{4}{17}-\frac{19}{34}i\)
Step-by-step explanation:
1. Approach
To divide complex numbers, first one must set the problem up as a fraction. The one will multiply the fraction by the complex conjugate. A complex conjugate is a complex number with the imaginary part multiplied by negative one. Since a number over itself equals one, this will ensure that the expression remains true. When one multiplies by the complex conjugate, the difference of squares property complex into play, therefore the denominator simplifies down to a real number (remember one can simplify the powers of (i)). Now all one has to do is divide each element in the complex number in the numerator by the real number in the denominator. If it does not divide evenly, one can just simply the fraction.
2. Solving
Set up as a fraction
\(\frac{3-4i}{8+2i}\)
Multiply by the complex conjugate
\(\frac{3-4i}{8+2i}*\frac{8-2i}{8-2i}\)
Simplify
\(\frac{(3-4i)(8-2i)}{(8+2i)(8-2i)}\)
\(\frac{24-6i-32i+8i^{2}}{64-4i^{2}}\)
\(\frac{24-6i-32i-8}{64-4(-1)}\)
\(\frac{16-38i}{64+4}\)
\(\frac{16-38i}{68}\)
\(\frac{8-19i}{34}\)
A large population has a bell-shaped distribution with a mean of 200 and a standard deviation of 40. Which one of the following intervals would contain approximately 95% of the measurements?
a. (160, 240)
b. (140, 260)
c. (120, 280)
d. (200, 320)
Answers
The intervals would contain approximately 95% of the measurements will be (120, 280). Then the correct option is C.
What is a normal distribution?The Gaussian Distribution is another name for it. The most significant continuous probability distribution is this one. Because the curve resembles a bell, it is also known as a bell curve.
In numerical documentation, these realities can be communicated as follows, where Pr(X) is the likelihood capability, Χ is a perception from an ordinarily circulated irregular variable, μ (mu) is the mean of the dispersion, and σ (sigma) is its standard deviation:
The interval for 95% will be given as,
Pr(X) = μ ± 2σ
Pr(X) = 200 ± 2(40)
Pr(X) = 200 ± 80
Pr(X) = (200 - 80, 200 + 80)
Pr(X) = (120, 280)
The intervals would contain approximately 95% of the measurements will be (120, 280). Then the correct option is C.
More about the normal distribution link is given below.
https://brainly.com/question/12421652
#SPJ5
Find the surface area of the cylinder.
Answers
Answer:
\(A=227.84\ inch^2\)
Step-by-step explanation:
Given that,
The diameter of the cylinder, d = 5 inch
Hight, h = 12 m
Radius, r = d/2 = 2.5 m
We need to find the surface area of the cylinder. The formula for the surface area of the cylinder is given by :
\(A=2\pi rh+2\pi r^2\\\\A=2\times \dfrac{22}{7} \times 2.5\times 12+2\pi \times 2.5^2\\\\A=227.84\ inch^2\)
So, the lateral surface area of the cylinder is equal to \(227.84\ inch^2\).
Answer question (i will give thanks and give a branliest who answers it correctly
Answers
Answer:
B because 4n + 2 is the only algebraic expression on there, therefore, B is the answer.
Which expressions are equivalent to 4(4x + 2y + x − y)? (1 point)
Group of answer choices
4(3x + y) and 12x + 4y
4(3x + 3y) and 12x + 12y
4(5x + y) and 20x + 4y
4(5x + 3y) and 20x + 12y
Answers
=4*4x+4*2y+4*x-4*y
=16x+8y+4x-4y
=16x+4x+8y-4y
=20x+4y
donc la bonne reponse est la 3
4(5x+y)*
=4*5x+4*y
=20x+4y
The value of a coin in 2010 was $40. The value of the coin has increased in value at a rate of 16.9% annually.
What was the value of the coin in 2019?
Enter your answer in the box rounded to the nearest dollar.
Answers
The value of the coin in 2019 would be approximately $132.
To calculate the value of the coin in 2019, we need to consider the annual increase rate of 16.9% from 2010 to 2019. We can use the compound interest formula to find the final value.
Starting with the initial value of $40 in 2010, we can calculate the value in 2019 as follows:
Value in 2019 = Initial value * (1 + Rate)^n
where Rate is the annual increase rate and n is the number of years between 2010 and 2019.
Plugging in the values:
Value in 2019 = $40 * (1 + 0.169)^9
Value in 2019 ≈ $40 * 2.996
Value in 2019 ≈ $119.84
Rounding the value to the nearest dollar, we get approximately $120. Therefore, the value of the coin in 2019 would be approximately $120.
However, please note that the exact value may vary depending on the specific compounding method and rounding conventions used.
for such more questions on value
https://brainly.com/question/843074
#SPJ8
Zoe wrote Three-fifths of her essay in 30 minutes. Assuming she wrote the paper at a constant rate the entire time, which expression can be used to determine the fraction of her essay she wrote each minute? 30 divided by three-fifths 30 times three-fifths Three-fifths divided by 30 Five-thirds divided by 30\
Answers
Answer:
1/50 (i think)
Step-by-step explanation:
What is the distance between these two points?
Answers
extra characters (this is not part of the answer)
Answer:
Step-by-step explanation:
The two points are (-6,8) and (8,0)
we can find the distance thanks to this formula
√(x1-x2)^2 + (y1-y2)^2 where x and y indicate the coordinates of the two points
√(-6-8)^2 + (8)^2 = √196 + 64 = √260 ≃ 16,12
During practice, the players on a softball team warm up by running the bases. This graph shows the relationship between the number of hours, x, of practice the players attend and the number of minutes, y, the players spend running the bases.
How many minutes do the players spend running the bases during each hour of practice?
Answers
The number of minutes that the players spend running bases during each hour of practice is the constant of proportionality of the proportional relationship.
What is a proportional relationship?A proportional relationship is defined as follows:
y = kx.
In which k is the constant of proportionality.
In the context of this problem, the variables x and y are given as follows:
Variable x: number of hours.Variable y: time spent running the bases.The equation for the constant is given as follows:
k = y/x.
Representing the hourly time spent running times, you can calculate it taking any point (x,y) on the graph of the function.
More can be learned about proportional relationships at https://brainly.com/question/10424180
#SPJ1
God (56) 8. Write the equation of this line in slope-intercept form. у - Х
Answers
In order to find the line equation, we need to choose 2 points along the line, for instance,
the points
\(\begin{gathered} (x_1,y_1)=(0,1)_{} \\ (x_2,y_2)=(1,3)_{} \end{gathered}\)Then, the slope m of the line will be given by
\(m=\frac{y_2-y_1}{x_2-x_1}=\frac{3-1}{1-0}\)which gives
\(m=\frac{2}{1}=2\)Then, the line has the form
\(y=mx+b\Rightarrow y=2x+b\)We can find the y-intercept denoted by b by substituting one of the two points. For instance, if we substitute point (0,1) into the last result, we get
\(\begin{gathered} 1=2(0)+b \\ \text{then} \\ b=1 \end{gathered}\)Therefore, the line equation in slope-intercept form is given by:
\(y=2x+1\)
Which of the following best describes the solution to the equation below? -4(4x + 9) = -2(8x + 18)
PLEASE SHOW HOW YOU GOT THE ANSWER
Answers
To find this, you first want to multiply the parenthesis by the external numbers on each side.
-4(4x + 9) = -16x - 36.
-2(8x + 18) = -16x - 36.
We are left with the equation -16x -36 = -16x -36. We are already given the answer here, but we can rewrite it to make it more clear.
We start by isolating the x variables by adding 36 to each side: (-16x - 36) + 36 = (-16x - 36) + 36. This leaves us with -16x = -16x. We can simplify this further by dividing by negative 16: -16x/-16 = x. This leaves us with the equation x = x. This equation is true for every single real number.
I hope this helps, if you have any questions let me know.
A restaurant stores flour, rice, and sugar in three different cylindrical containers.
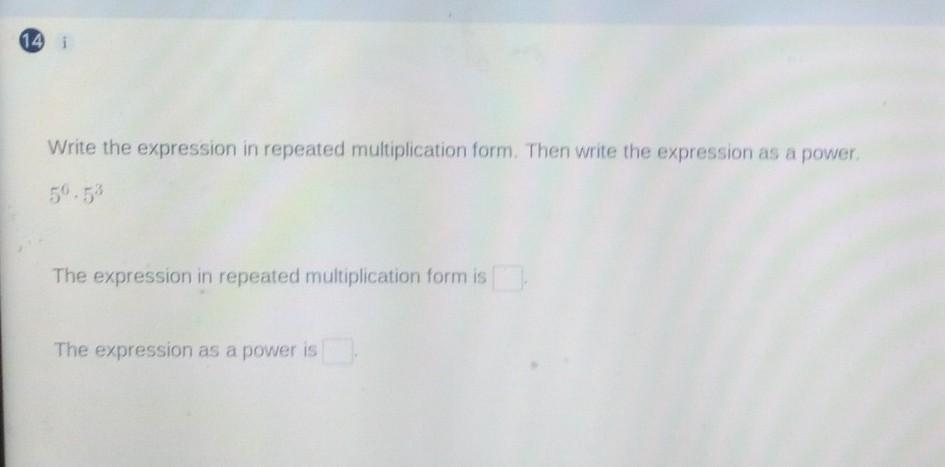
Answers
The height of the rice cylinder is 12in.
The volume of the flour cylinder is 50.24 in.
What is a cylinder?A cylinder is a 3-D figure that has a radius and a height.
The volume of a cylinder is given as πr²h.
Example:
The volume of a cup with a height of 5 cm and a radius of 2 cm is
Volume.
= 3.14 x 2 x 2 x 5
= 62.8 cm³
We have,
Sugar cylinder:
radius = 2.5 in
height = 8 in
Volume.
= πr²h
= 3.14 x 2.5 x 2.5 x 8
= 157 in²
Rice cylinder:
radius = 2.5 in
height = h
Volume = πr²h
Volume = 235.5 in²
πr²h = 235.5
3.14 x 2.5 x 2.5 x h = 235.5
196.26 x h = 235.5
h = 12 in
Flour cylinder:
Area of base = 12.56 in²
height = 4 in
Volume = x
Area of base = πr²
12.56 = 3.14 x r²
r² = 12.56/3.14
r² = 4
r = 2
Now,
Volume.
= πr²h
= 3.14 x 2 x 2 x 4
= 50.24 in²
Thus,
The solution for each cylinder is given above.
Learn more about cylinder here:
https://brainly.com/question/15891031
#SPJ9